Цилиндр, конус, шар, развёртка цилиндра и конуса
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В курсе математики для б класса рассматриваются только прямые цилиндры и конусы
.
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Развертка цилиндра приведена схематически.
Развертка конуса приведена схематически.
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
где C — длина окружности, H
— высота цилиндра, R — радиус окружности основания.Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
где R — радиус шара.
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания н высоты.
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
где R — радиус основания, H — высота конуса.
Правило. Объем шара
произведения числа Пи на куб радиуса.
где R — радиус шара.
Цилиндр. История возникновения — презентация онлайн
1. Цилиндр
Министерство общего и профессионального образованияСвердловской области
ГБПОУ СО ”Красноуфимский аграрный колледж”
Цилиндр
Выполнили:
студенты группы 12-Э
Галимов И.
 И
ИКуликов И.Д
Руководитель:
Просвирова О.И
преподаватель математики
Красноуфимск, 2019
2. Цель и Задачи
ЦельРассмотреть ,где встречается геометрическая фигура
цилиндр в нашей повседневной жизни
Задачи
Использовать интернет-ресурсы или литературу по
теме
Узнать, как появилась геометрическая фигура
цилиндр, узнать историю ее развития
Рассмотреть, где используется цилиндр
Узнать какие теоремы есть ,относящиеся к данной
фигуре
3. Актуальность
В настоящее время цилиндрические формывстречаются очень часто. Например: кружка , трубы,
ручка и многое другое. И поэтому возникла
потребность в изучении геометрической фигуры
цилиндр.
4. История возникновения
Когда стали строить здания из камня пришлосьперетаскивать каменные глыбы. Для этого издавна
применяли катки. И было замечено, перекатка
тяжелого камня становилось легче, если для катка
взято прямое дерево и от него отрезан кусок с почти
одинаковой толщиной в начале и конце.
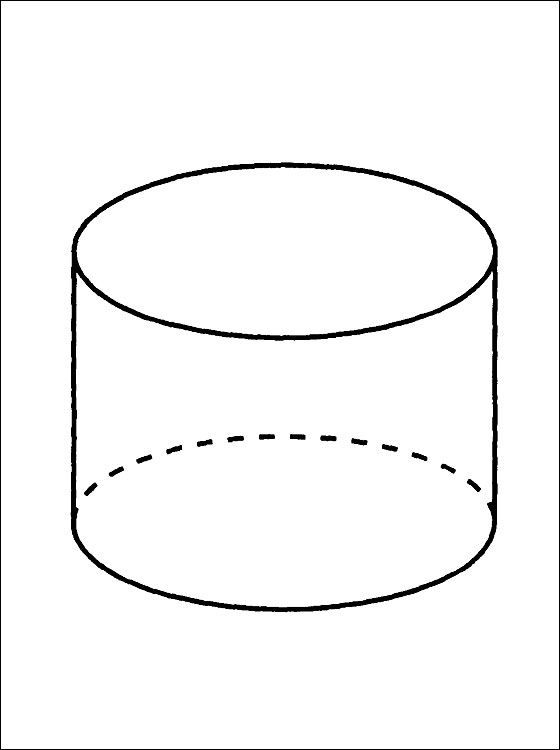 Так люди
Так людипознакомились с одной из важнейших фигур –
цилиндром.
Скалками цилиндрической формы пользовались и
женщины, раскатывая бельё после стирки.
5. Теоретический материал
Цилиндр — это геометрическое тело, ограниченноецилиндрической поверхностью и двумя
параллельными плоскостями, пересекающими ее.
Свойства
Основания равны и параллельны
Все образующие цилиндра равны и параллельны
друг другу
6. Формулы
Площадь боковой поверхностиSб=LH=2πrH
Площадь основания цилиндра
Sо=πR2
Формула площади цилиндра
S=Sб+2Sо=2πRH+2πR2
Формула объема цилиндра
V=Sо⋅H=πR2H
Где H-высота
L-длина основания
R-радиус
7. Теоремы
Теорема 1Площадь боковой поверхности цилиндра
определяется как произведение длины окружности,
ограничивающей основание цилиндра на его высоту..
Теорема 2
Объем цилиндра определяется как произведение
площади основания цилиндра на его высоту.

8. В жизни и творчестве
И. П. Мартос. Надгробие Кожуховой. Модель. 1827Храм Исиды на острове Филе.
12. Стихи
— Цилиндр, что такое? — спросил я у папы. Отецрассмеялся: — Цилиндр, это шляпа. Чтобы иметь
представление верное, Цилиндр, скажем так, это
банка консервная. Труба парохода — цилиндр, труба
на нашей крыше — тоже, Все трубы на цилиндр
похожи. А я привёл пример такой — Калейдоскоп
любимый мой, глаз от него не оторвёшь, И тоже на
цилиндр похож.
Фигуры все запомнить мне Труба подзорная поможет!
Она – цилиндр, например! И, кстати! В ней круг есть
тоже!
13. Цитата
Геометрия — это искусство хорошо рассуждать наплохо выполненных чертежах.
/Нильс Г. Абель/
14. Заключение
Такимобразом при изучении данной
геометрической фигуры мы узнали ,что
такое цилиндр, историю возникновения
и повторили формулы и теоремы.
Цилиндрическая фигура. Цилиндр как геометрическая фигура
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис. ).
).Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого — это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр.
 Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры. - Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
- Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.
Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания — R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая — L.
- Высота — H.
- Площадь основания — S осн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра — h 1 ,h 2 (минимальная и максимальная).
- Площадь боковой поверхности — S бок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры — V.

- Площадь полной поверхности — S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.
- Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
- Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение.
 Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем — для прямого.
Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг — проведение сечения через основание фигуры.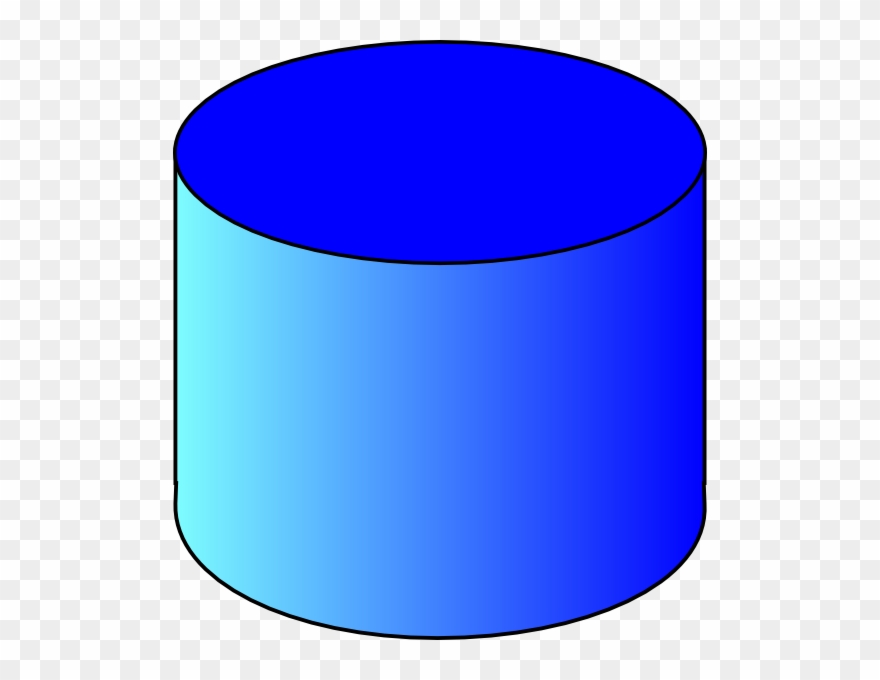 Необходимо рассмотреть получившуюся плоскость.
Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC — прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD — трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
Необходимо найти полную площадь стереометрической фигуры.
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.
На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О 1 являются его основаниями.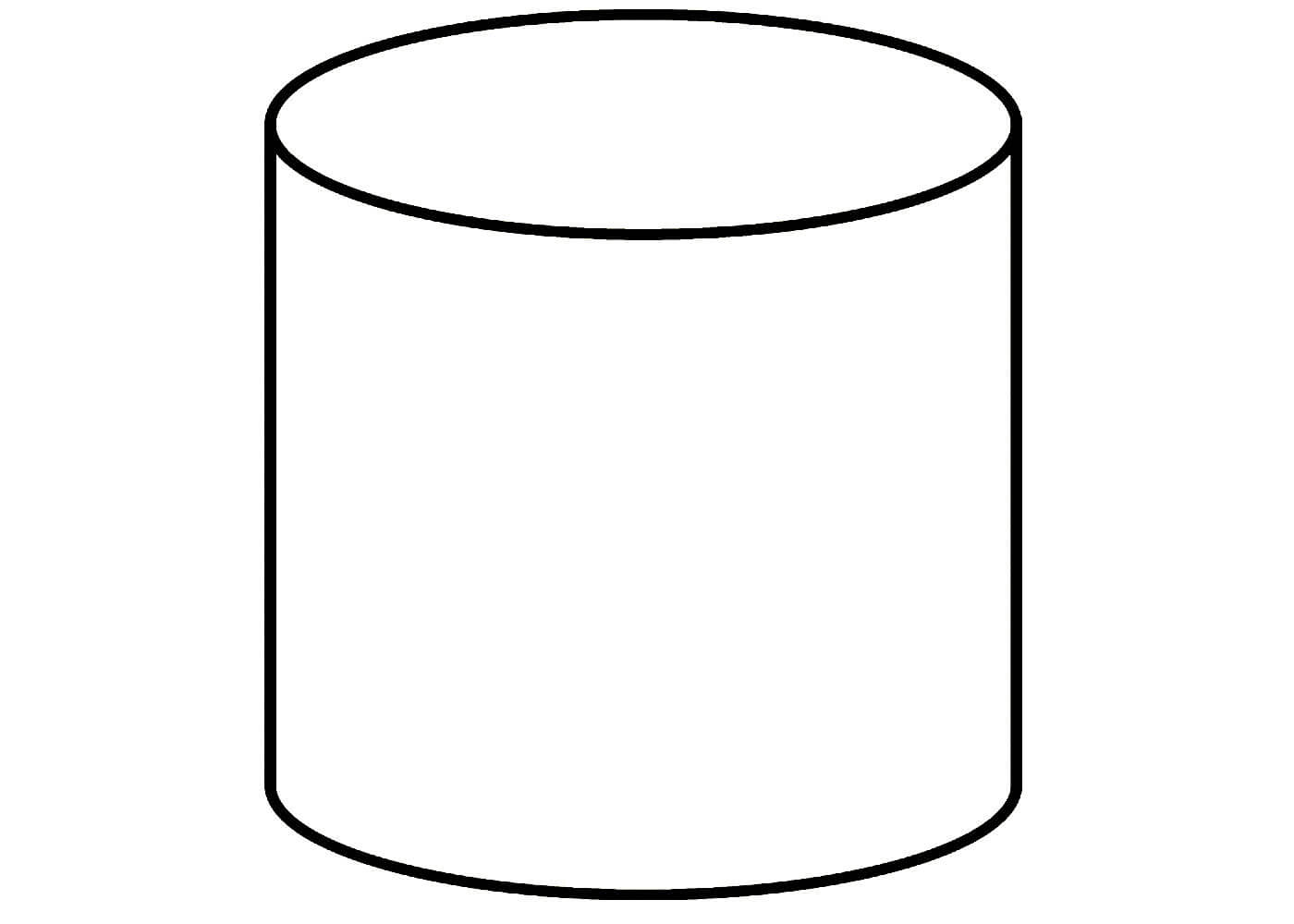
Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.
Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
В частности, для прямого кругового цилиндра:
P = 2πR, и S b = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
S p = 2πRh + 2πR 2 = 2πR(h + R)
Для нахождения объёма наклонного цилиндра существуют две формулы.
Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):
V = Sh = S l sin α,
где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.
Для прямого цилиндра h = l.
Формула для нахождения объёма кругового цилиндра выглядит следующим образом:
V = π R 2 h = π (d 2 / 4)h,
где d – диаметр основания.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Конспект урока математики «Цилиндр-геометрическая фигура»
Урок математики в условиях ФГОС.
Предмет: математика
УМК: «Начальная школа XXI века» (учебник и рабочая тетрадь 4 класс)
Авторы учебника и рабочей тетради: В.Н.Рудницкая, Т.В.Юдачева
Тема урока: «Цилиндр — объемная геометрическая фигура»
Класс: 4
Тип урока: урок открытия новых знаний
Методы: словесные, частично-поисковые, проблемные, игровые, практические, объяснительно-иллюстративные, репродуктивные
Форма: индивидуальная, парная, фронтальная
Оборудование: компьютер, мультимедийный проектор, презентация, модели объемных геометрических фигур, пластилин, паспорт фигуры.
Цель урока: создание условий для расширения знаний об объемных геометрических фигурах, формирования представлений о фигуре цилиндр, ее признаков на уровне ощущений и представлений.
Задачи:
образовательная: формирование умений классифицировать фигуры по различным признакам, распознавать объемную фигуру цилиндр по ее признакам.
развивающая: развитие устойчивости внимания, зрительной памяти, логического мышления, устной и письменной речи; общеучебных умений и навыков (умение слушать и слышать, работать в заданном темпе, контролировать действия и оценивать свою работу),
воспитывающая: формирование коммуникативных навыков и навыков учебного труда, вовлечение в активную практическую деятельность, воспитание интереса к предмету.
Познавательные УУД:
самостоятельно выделять и формулировать познавательную цель раздела, урока;
выбор наиболее эффективных способов решения задачи для получения результата;
контролировать и оценивать процесс и результат своей деятельности, в паре, класса в целом;
извлекать необходимую информацию и делать вывод с помощью наблюдения, сравнения, анализа, моделирования;
использовать различные способы для получения информации и работы с ней, использовать справочные материалы, умение ориентироваться в рисунках,таблицах;
учиться формулировать связный ответ на поставленный вопрос, высказывать свое мнение, слышать и слушать, грамотно владеть речью
Регулятивные УУД:
определять и формулировать цель деятельности на уроке с помощью учителя;
учиться работать по предложенному учителем плану;
планировать свои действия в соответствии с поставленной задачей, принимать и сохранять задачу урока;
отслеживать уровень овладения учебным материалом контролировать;
проговаривать алгоритм действий на уроке
Личностные УУД:
развивать интеллектуальные умения: анализировать и обобщать;
развивать познавательную активность, память, внимание, речь и интерес к чтению;
создать условия для развития умения формулировать собственную точку зрения, высказывать ее и аргументировать;
определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве, способность к самооценке на основе критерия успешности учебной деятельности;
проявлять положительное отношение к урокам математики
Коммуникативные УУД:
содействовать развитию умения сотрудничать с товарищем при работе в паре и класса в целом;
договариваться и приходить к общему решению в совместной деятельности;
осознавать ценность совместной деятельности; уважительного отношения друг к другу
Ход урока
1.Орг. момент. Мобилизующий этап.
Долгожданный дан звонок,
Начинается урок!
Вы проверьте, все готово?
Все на месте ли у вас?
Пожелаю вам удачи,
За работу, в добрый час!
Глубоко вдохните, настройтесь на работу. Я желаю вам хорошего настроения!
-Присаживайтесь!
-И мы начинаем урок математики.
-Скажите, для чего нужно изучать математику?
-Каждый день в мире происходят открытия. Открывается что-то совершенно новое, не изученное, никому ранее не известное, но очень интересное. Сегодня мы с вами тоже постараемся открыть много нового, интересного для себя, и будем помогать в этом друг — другу, если необходимо.
-Поднимите руки, кто готов отправиться за новыми знаниями? (поднимают руку).
2.Устный счет.
-Сегодня я приглашаю вас в удивительный мир открытий одной из областей наук. А какой, вы узнаете, если верно выполните задания.
(на слайде даются выражения на умножения и деления, дети по одному выходят и выполняют действия)
— Расставьте значения выражений в порядке увеличения, если вы все верно выполните, то сможете прочесть получившееся слово.
-Какое слово получилось? (геометрия)
3. Мотивационный этап. Актуализация знаний. Формулирование темы и цели урока.
-Какие ассоциации возникают со словом геометрия? (варианты ответов, подвести к слову фигуры)
-Какое значение имеет слово «фигура?» (шахматная фигура, человеческая фигура, геометрическая фигура) .
-Наука геометрия-это удивительно интересная наука. С ней вы будете встречаться до 11 класса. А чем же она удивительна? Оказывается, в ней всё необычно, даже простые обычные предметы, становятся необычными.
-Рассмотрите и назовите предметы (называют)
(на слайде предметы имеющие форму геометрических фигур: куба, пирамиды, сферы,конуса,цилиндра)
-Что необычного в этих предметах? (предметы имеют форму геометрических фигур)
-В форме каких геометрических фигур представлены предметы? (называют предмет и фигуру напоминающую его: куб, пирамида, сфера, конус)
(учитель выставляет поочередно реальные модели фигур)
(ученик выходит к моделям и распределяет фигуры по группам, показывает признаки фигуры, доказывая свой выбор)
-По какому признаку можно объединить эти фигуры? (объемные, возможен вариант по цвету, размеру)
-По каким признакам можно разделить фигуры на 2 группы? (по основанию:1группа-в основании окружность, 2группа-многоугольник; по вершине:1группа-общая вершина 1 точка, 2группа-несколько вершин; по ребрам: 1группа-есть ребра, 2группа-нет ребер)
-Мы еще раз повторили и закрепили знания о геометрических фигурах и их признаках.
4. Открытие нового знания и способа действия.
-Я задумала геометрическую фигуру, отгадайте какую?
Присмотрись, стоит ведро —
Сверху крышка, снизу дно.
Два кружка соединили,
И фигуру получили.
(Цилиндр).
— Как вы думаете, какая фигура называется цилиндром?
-Какие предметы из окружающей среды по форме напоминают цилиндр? (перечисляют)
-Посмотрите, какие еще существуют предметы в форме цилиндра.
-Кто догадался, о какой геометрической фигуре пойдет речь на уроке? (цилиндр)
-Сформулируйте тему урока?
-Какие цели поставим перед собой? (учащиеся определяют тему и задачи урока)
-А кто знает, откуда произошло слово «цилиндр»? (предположения детей)
-Оказывается слово «цилиндр» произошло от греческого «кюлиндрос», означающий «валик», «каток». Очень давно, когда не было ещё машин и тракторов, и никакой другой техники, люди, чтобы перетащить тяжёлый груз с одного места на другое, использовали катки из дерева. Они подыскивали прямое дерево и отрезали от него кусок. Этот кусок и служил катком.
-А знаете ли вы, что в руках древнеегипетских изображений фараонов можно увидеть два мистических цилиндра. Они защищают от различных излучений и множества тяжелых болезней.
-А вот самый большой в мире аквариум работает в США. В 32 миллионах литров воды обитает 120000 растений и животных, там живут даже китовые акулы. Но самое главное, этот аквариум имеет форму цилиндра.
-А первое мороженое в России появилось в 1937 году. Это было глазированное эскимо с деревянной палочкой внутри, в форме меленького цилиндра.
-А на рубеже 18-19 веков мужчины многих стран носили твердые шляпы с небольшими полями, которые так и назывались цилиндром, из-за большого сходства с геометрической фигурой цилиндр.
-Вот какая интересная и необычная фигура цилиндр.
5. Физминутка.
(учащиеся вместе с учителем выполняют движения)
А теперь все дружно встали!
Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас.
Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности. Цилиндр стал маленькой подарочной коробочкой.
Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… (хлопок) сюрприз выскакивает из коробочки!
6. Пробное учебное действие по теме урока (в парах)
-Сейчас я предлагаю сконструировать модель цилиндра из пластилина.
-Рассмотрим, из скольки частей состоит цилиндр? (3частей)
-Назовите эти части? (2 основания и 1боковая часть)
-Какой формы основание? (круглой)
-Какой формы боковая часть? (прямоугольной)
-Выполните модель цилиндра (выполняют 2 мин.)
-Покажите ваши цилиндры (показывают)
-Рассмотрите модели всего класса и скажите:
-Чем похожи ваши цилиндры? (формой, из одного материала: пластилина, объемные, катятся, не прозрачные,имеют 2 основания, 2 боковые поверхности)
-Чем отличаются? (размером, цветом, по весу)
-Сейчас вы поработаете в паре.
-Исследуя свои модели, составьте «паспорт» цилиндра и выясните какая фигура называется цилиндром?(у каждого на парте по одному паспорту,дети работают совместно в паре)
ПАСПОРТ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ
(на парте)
(Заполненный паспорт)
1. Название фигурыЦилиндр
2.Плоская или объемная геометрическая фигура
Это объемная геометрическая фигура
3.Количество оснований
Состоящая из двух оснований
4.В виде какой фигуры представлены основания?
В виде кругов
5.Количество боковых поверхностей
Имеющая одну боковую поверхность
6.В виде какой фигуры представлена боковая поверхность?
В виде прямоугольника
7.Количество вершин
Имеет множество вершин
-Проверим вашу работу (по каждому пункту отвечают, показывая и доказывая на своей модели из пластилина)
(сравнивают с правильным паспортом на слайде)
-Пользуясь «паспортом» фигуры, сделайте вывод: какая фигура называется цилиндром?
(дети по «паспорту» формулируют правило: цилиндр-это объемная геометрическая фигура, состоящая из двух оснований в виде кругов и одной боковой поверхности в виде прямоугольника)
(на слайде выходит правило по частям, исходя из ответов детей).
-Прочтем еще раз, какую фигуру называем цилиндром (читает ученик)
7. Закрепление и расширение знаний
Поиграем в игру «Молчанка».
Все молчат, работают только руки.
-Покажите руками цилиндр.
-Покажите верхнее основание.
-Покажите нижнее основание.
-Покажите боковую часть цилиндра.
— Поставьте самый высокий цилиндр, а слева от него — самый низкий. Покажите, у какого цилиндра самое большое основание, а у какого самое маленькое?
-Покатайте ваши цилиндры.
-Молодцы! Отлично справились, игра окончена.
— Откройте учебник, рабочую тетрадь.
— Найдите тему нашего урока.
— Назовите страницу? (43)
-Найдите №123
-Прочитайте задание. Что требуется выполнить?
-Найдите 2 цилиндра.
-Какие они по счету?(1 и 3)
-По каким признакам узнали цилиндр?
-Закрасьте цилиндры, используя 2 любых цвета, показав основания и боковую часть фигуры.
№ 124 (САМОСТОЯТЕЛЬНО)
Проверяем? (круг)
-Найдите № 125 (один из учеников работает у доски)
-Прочитайте задание.
-Какой предмет изображен?(стакан)
-Какой формы стакан?( цилиндрической)
-В каком масштабе представлен стакан?(1:5)
-Что значит 1:5?(объясняют соотношение 1 к 5)
-Что необходимо выполнить, чтобы вычислить масштаб? (измерить высоту)
— Какова высота стакана?(2см)
-Вычислите и запишите масштаб (учащиеся самостоятельно выполняют вычисления в тетради,1 ученик работает у доски)
№ 126
-Что такое диаметр? (озвучивают правило)
-Как вычислить радиус, зная диаметр (измерить диаметр и разделить на 2 равные части,от центральной точки провести окружность через точки)
-Выполните вычисления (учащиеся самостоятельно выполняют вычисления в тетради,1 ученик работает у доски)
-Проверка
8. Аналитический этап урока. Рефлексия учебной деятельности на уроке.
Подведем итог нашей работы на уроке
Вспомните, какой была тема урока (ответ учащихся)
Какую цель ставили перед собой? (ответ учащихся)
-Достигли ли мы этих целей? (ответ учащихся)
-Каким был наш урок? (ответ учащихся)
-Что было особенно интересным? (ответ учащихся)
-Какими были вы на уроке? (ответ учащихся)
-Вы большие молодцы! Сегодня на уроке вы открыли много нового, интересного и полезного. Очень дружно, активно работали, помогали друг другу.
-Оцените свои достижения на уроке. Кто доволен своей работой, поднимите красный смайлик, синий — если некоторые вопросы вызвали затруднения.
(оценивание, дом. задание )
-Я благодарю всех за урок!
Литература:
1. Математика: 4 класс: учебник для учащихся общеобразовательных организаций: в 2ч. Ч.2/ В.Н.Рудницкая, Т.В. Юдачёва.- 4-е изд., перераб. – М.: Вентана – Граф, 2014. – 160 с.: ил.
2.Математика: 4 класс: Рабочая тетрадь по математике: в 2ч.Ч.2/ В.Н.Рудницкая, Т.В. Юдачёва. М.: Вентана – Граф,2015.
3.Математика: 4 класс: методическое пособие / В.Н. Рудницкая, Т.В. Юдачёва. – 3-е изд., перераб. – М.: Вентана – Граф, 2015. – 272 с.: ил.
(в конспекте урока представлены краткие ответы учащихся, необходимо добиваться полных, развернутых ответов)
Как найти длину образующей цилиндра. Цилиндр как геометрическая фигура
Стереометрия − это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.
В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, многие детали машин имеют форму цилиндра или представляют собой некоторое их сочетание, а величественные колонны храмов и соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.
Греч. − кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить, катать).
У Евклида цилиндр получается вращением прямоугольника. У Кавальери − движением образующей (при произвольной направляющей − «цилиндрика»).
Цель данного реферата рассмотреть геометрическое тело – цилиндр.
Для достижения данной цели необходимо рассмотреть следующие задачи:
− дать определения цилиндра;
− рассмотреть элементы цилиндра;
− изучить свойства цилиндра;
− рассмотреть виды сечения цилиндра;
− вывести формулу площади цилиндра;
− вывести формулу объема цилиндра;
− решить задачи с использованием цилиндра.
1.1. Определение цилиндра
Рассмотрим какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плокости α, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной линии l проведем прямые, параллельные прямой S; образованная этими прямыми поверхность α называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s 1 , s 2 , s 3 ,… − ее образующими.
Если направляющая является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских полос, заключенных между парами параллельных прямых, и называется призматической поверхностью. Образующие, проходящие через вершины направляющей ломаной, называются ребрами призматической поверхности, плоские полосы между ними − ее гранями.
Если рассечь любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее образующим, то получим линию, которая также может быть принята за направляющую данной поверхности. Среди направляющих выделяется та, которая, получается, от сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое сечение называется нормальным сечением, а соответствующая направляющая − нормальной направляющей.
Если направляющая − замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность называется замкнутой (выпуклой) призматической или цилиндрической поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя плоскостями, параллельными между собой, но не параллельными образующим.
В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями α и α», и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом − призмой.
Цилиндрическое тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований.
Цилиндром (точнее, круговым цилиндром) называется геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис. 1).
Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.
Так как параллельный перенос есть движение, то основания цилиндра равны.
Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях.
Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси (рис. 2).
Рис. 2 − Прямой цилиндр
В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.
Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.
В частности, если основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом) цилиндре; если эллипс − то эллиптическом.
1. 3. Сечения цилиндра
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 3, а). Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
а)б)
в) г)
Рис. 3 – Сечения цилиндра
В частности, прямоугольником является осевое сечение. Это − сечение цилиндра плоскостью, проходящей через его ось (рис. 3, б).
Сечение цилиндра плоскостью, параллельной основанию − круг (рис 3, в).
Сечение цилиндра плоскостью не параллельной основанию и его оси − овал (рис. 3г).
Теорема 1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Доказательство. Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью β с окружностью основания. Теорема доказана.
Площадь боковой поверхности цилиндра.
За площадь боковой поверхности цилиндра принимается предел, к которому стремится площадь боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон основания этой призмы неограниченно возрастет.
Теорема 2. Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S бок.ц = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).
А) б)
Рис. 4 − Площадь боковой поверхности цилиндра
Доказательство.
Пусть P n и Н соответственно периметр основания и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда площадь боковой поверхности этой призмы S бок.ц − P n H. Предположим, что число сторон многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда периметр P n стремится к длине окружности С = 2πR, где R- радиус основания цилиндра, а высота H не изменяется. Таким образом, площадь боковой поверхности призмы стремится к пределу 2πRH, т. е. площадь боковой поверхности цилиндра равна S бок.ц = 2πRH. Теорема доказана.
Площадь полной поверхности цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра равна πR 2 , следовательно, площадь полной поверхности цилиндра S полн вычисляется по формуле S бок.ц = 2πRH+ 2πR 2 .
а) б)Рис. 5 − Площадь полной поверхности цилиндра
Если боковую поверхность цилиндра разрезать по образующей FT (рис. 5, а) и развернуть так, чтобы все образующие оказались в одной плоскости, то в результате мы получим прямоугольник FTT1F1, который называется разверткой боковой поверхности цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания цилиндра, следовательно, FF1=2πR, а его сторона FT равна образующей цилиндра, т. е. FT = Н (рис. 5, б). Таким образом, площадь FT∙FF1=2πRH развертки цилиндра равна площади его боковой поверхности.
1.5. Объем цилиндра
Если геометрическое тело простое, то есть допускает разбиение на конечное число треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.
Данное тело имеет объем V, если существует содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколько угодно мало отличающимися от V.
Применим это определение к нахождению объема цилиндра с радиусом основания R и высотой Н.
При выводе формулы для площади круга были построены такие два n-угольника (один − содержащий круг, другой − содержащийся в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть Р − многоугольник, содержащий круг, а Р» − многоугольник, содержащийся в круге (рис. 6).
Рис. 7 − Цилиндр с описанной и вписанной в него призмой
Построим две прямые призмы с основаниями Р и Р» и высотой Н, равной высоте цилиндра. Первая призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SН. Согласно определению объем цилиндра
V = SH = πR 2 H.
Итак, объем цилиндра равен произведению площади основания на высоту.
Задача 1.
Осевое сечение цилиндра − квадрат, площадь которого Q.
Найдите площадь основания цилиндра.
Дано: цилиндр, квадрат − осевое сечение цилиндра, S квадрата = Q.
Найти: S осн.цил.
Сторона квадрата равна . Она равна диаметру основания. Поэтому площадь основания равна .
Ответ: S осн.цил. =
Задача 2.
В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Дано: цилиндр, правильная шестиугольная призма вписанная в цилиндр, радиус основания = высоте цилиндра.
Найти: угол между диагональю ее боковой грани и осью цилиндра.
Решение: Боковые грани призмы − квадраты, так как сторона правильного шестиугольника, вписанного в окружность, равна радиусу.
Ребра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А это угол равен 45°, так как грани − квадраты.
Ответ: угол между диагональю ее боковой грани и осью цилиндра = 45°.
Задача 3.
Высота цилиндра 6см, радиус основания 5см.
Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Дано: Н = 6см, R = 5см, ОЕ = 4см.
Найти: S сеч.
S сеч. = КМ×КС,
ОЕ = 4 см, КС = 6 см.
Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),
треугольник ОЕК − прямоугольный.
Из треугольника ОЕК, по теореме Пифагора:
КМ = 2ЕК = 2×3 = 6,
S сеч. = 6×6 = 36 см 2 .
Цель данного реферата выполнена, рассмотрено такое геометрическое тело, как цилиндр.
Рассмотрены следующие задачи:
− дано определение цилиндра;
− рассмотрены элементы цилиндра;
− изучены свойства цилиндра;
− рассмотрены виды сечения цилиндра;
− выведена формула площади цилиндра;
− выведена формула объема цилиндра;
− решены задачи с использованием цилиндра.
1. Погорелов А. В. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений, 1995.
2. Бескин Л.Н. Стереометрия. Пособие для учителей средней школы, 1999.
3. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Киселева Л. С., Позняк Э. Г. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений, 2000.
4. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия: учебник для 10-11 классов общеобразовательных учреждений, 1998.
5. Киселев А. П., Рыбкин Н. А. Геометрия: Стереометрия: 10 – 11 классы: Учебник и задачник, 2000.
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.
На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О 1 являются его основаниями.
Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.
Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
В частности, для прямого кругового цилиндра:
P = 2πR, и S b = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
S p = 2πRh + 2πR 2 = 2πR(h + R)
Для нахождения объёма наклонного цилиндра существуют две формулы.
Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):
V = Sh = S l sin α,
где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.
Формула для нахождения объёма кругового цилиндра выглядит следующим образом:
V = π R 2 h = π (d 2 / 4)h,
где d – диаметр основания.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Существует большое количество задач, связанных с цилиндром. В них нужно находить радиус и высоту тела или вид его сечения. Плюс ко всему, иногда требуется вычислить площадь цилиндра и его объем.
Какое тело является цилиндром?
В курсе школьной программы изучается круговой, то есть являющийся таковым в основании, цилиндр. Но выделяют еще и эллиптический вид данной фигуры. Из названия ясно, что его основанием будет эллипс или овал.
Оснований у цилиндра два. Они равны друг другу и соединены отрезками, которые совмещают соответствующие точки оснований. Они называются образующими цилиндра. Все образующие параллельны друг другу и равны. Именно они составляют боковую поверхность тела.
В общем случае цилиндр — это наклонное тело. Если образующие составляют прямой угол с основаниями, то говорят уже о прямой фигуре.
Интересно, что круговой цилиндр является телом вращения. Он получается от поворота прямоугольника вокруг одной из его сторон.
Основные элементы цилиндра
Основные элементы цилиндра выглядят следующим образом.
- Высота. Она является кратчайшим расстоянием между основаниями цилиндра. Если он прямой, то высота совпадает с образующей.
- Радиус. Совпадает с тем, который можно провести в основании.
- Ось. Это прямая линия, которая содержит центры обоих оснований. Ось всегда параллельна всем образующим. В прямом цилиндре она перпендикулярна основаниям.
- Осевое сечение. Оно образуется при пересечении цилиндра плоскостью, содержащей ось.
- Касательная плоскость. Она проходит через одну из образующих и перпендикулярна осевому сечению, которое проведено через эту образующую.
Как связан цилиндр с вписанной в него или описанной около него призмой?
Иногда встречаются задачи, в которых нужно вычислить площадь цилиндра, а известны при этом некоторые элементы связанной с ним призмы. Как соотносятся эти фигуры?
Если призма вписана в цилиндр, то ее основания — равные многоугольники. Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.
У описанной призмы в основаниях находятся правильные многоугольники. Они описаны около кругов цилиндра, являющихся его основаниями. Плоскости, которые содержат грани призмы, касаются цилиндра по образующим.
О площади боковой поверхности и основания для прямого кругового цилиндра
Если сделать развертку боковой поверхности, то получится прямоугольник. Его стороны будут совпадать с образующей и длиной окружности основания. Поэтому боковая площадь цилиндра будет равна произведению этих двух величин. Если записать формулу, то получится следующее:
S бок = l * н,
где н — образующая, l — длина окружности.
Причем последний параметр вычисляется по формуле:
l = 2 π * r,
здесь r — радиус окружности, π — число «пи», равное 3,14.
Поскольку основание — круг, то его площадь вычисляется с помощью такого выражения:
S осн = π * r 2 .
О площади всей поверхности прямого кругового цилиндра
Так как она образована двумя основаниями и боковой поверхностью, то нужно сложить эти три величины. То есть полная площадь цилиндра будет вычисляться по формуле:
S пол = 2 π * r * н + 2 π * r 2 .
Часто ее записывают в другом виде:
S пол = 2 π * r (н + r).
О площадях наклонного кругового цилиндра
Что касается оснований, то там все формулы те же, ведь они по-прежнему круги. А вот боковая поверхность уже не дает прямоугольника.
Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей.
Формула выглядит так:
S бок = х * Р,
где х — длина образующей цилиндра, Р — периметр сечения.
Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра. Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. Но его часто бывает достаточно для задач школьного курса:
l = π * (а + в),
где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек.
Площадь всей поверхности нужно вычислять с помощью такого выражения:
S пол = 2 π * r 2 + х * Р.
Чему равны некоторые сечения прямого кругового цилиндра?
Когда сечение проходит через ось, то его площадь определяется как произведение образующей и диаметра основания. Это объясняется тем, что оно имеет вид прямоугольника, стороны которого совпадают с обозначенными элементами.
Чтобы найти площадь сечения цилиндра, являющегося параллельным осевому, потребуется тоже формула для прямоугольника. В этой ситуации одна его сторона будет по-прежнему совпадать с высотой, а другая равна хорде основания. Последняя же совпадает с линией сечения по основанию.
Когда сечение перпендикулярно оси, то оно имеет вид круга. Причем его площадь такая же, как у основания фигуры.
Возможно еще пересечение под некоторым углом к оси. Тогда в сечении получается овал или его часть.
Примеры задач
Задание №1. Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.
Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.
Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.
Ответ: S пол = 50,24 см 2 .
Задание №2. Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.
Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.
Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.
Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.
Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность — 16. После извлечения квадратного корня остается 4. Это искомый катет.
Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2).
Ответ: S сеч равна 32 см 2 .
Задание №3. Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.
Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.
Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба — квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.
Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.
Сечение — это снова прямоугольник со сторонами 10 и 10√2. Его площадь легко сосчитать, перемножив эти значения.
Ответ. S сеч = 100√2 см 2 .
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3.14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
%d1%84%d0%b8%d0%b3%d1%83%d1%80%d0%b0 %d1%86%d0%b8%d0%bb%d0%b8%d0%bd%d0%b4%d1%80 PNG, векторы, PSD и пнг для бесплатной загрузки
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
естественный цвет bb крем цвета
1200*1200
поп арт 80 х патч стикер
3508*2480
поп арт 80 х патч стикер
3508*2480
80 основных форм силуэта
5000*5000
Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации
4167*4167
схема бд электронный компонент технологии принципиальная схема технологическая линия
2000*2000
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
поп арт 80 х патч стикер
2292*2293
мемфис бесшовной схеме 80s 90 все стили
4167*4167
поп арт 80 х патч стикер
2292*2293
80 е брызги краски дизайн текста
1200*1200
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
поп арт 80 х патч стикер
3508*2480
Элементы рок н ролла 80 х
1200*1200
поп арт 80 х патч стикер
3508*2480
скейтборд в неоновых цветах 80 х
1200*1200
поп арт 80 х патч стикер
3508*2480
поп арт 80 х патч стикер
2292*2293
3d модель надувной подушки bb cream
2500*2500
ТВ игра 80 х в стиле ретро
1200*1200
80 от большой распродажи постер
1200*1200
Тенденция персонажа мультфильма 80 х годов
2000*2000
80 летнего юбилея векторный дизайн шаблона иллюстрация
4083*4083
80 х годов стиль градиента стиль неоновый эффект слово дизайн
1200*1200
вектор скорости 80 значок
1024*1024
поп арт 80 х патч стикер
2292*2293
поп арт 80 х патч стикер
3508*2480
поп арт 80 х патч стикер
3508*2480
80 летие векторный дизайн шаблона иллюстрация
4167*4167
пентаграмма наклейки 80 х мультик звезд мультика стикер
2003*2003
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
непрерывный рисунок одной линии старого телефона винтаж 80 х 90 х годов стиль вектор ретро дизайн минимализм с цветом
3967*3967
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
поп арт 80 х патч стикер
2292*2293
поп арт 80 х патч стикер
3508*2480
номер 80 золотой шрифт
1200*1200
Ретро мода неоновый эффект 80 х тема художественное слово
1200*1200
Модель буквы м в стиле 80 х
1200*1200
bb крем ню макияжа постер Новый список преимущественный колос День святого
3240*4320
Золотая большая распродажа со скидкой до 80 с лентой
1200*1200
86 год лента годовщина
5000*3000
в первоначальном письме bd логотипа
1200*1200
80 лет юбилей красный шар вектор шаблон дизайн иллюстрация
4167*4167
80 летия золотой шар векторный дизайн шаблона иллюстрация
4083*4083
bb крем ню макияж косметика косметика
1200*1500
в эти выходные только мега продажи баннер скидки до 80 с
10418*10418
80 е в стиле ретро мода цвет градиент арт дизайн
1200*1200
ретро 80 х годов стиль текста эффект макет
3000*3000
Диско вечеринка арт дизайн
1200*1200
Тела вращения — Развертки — Mnogogranniki.ru
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон?
Одним лишь вращением мы можем создать новое геометрическое тело в пространстве.
Боковые поверхности цилиндра образуются за счет сторон вращающегося прямоугольника.
Официальное определение для таких геометрических тел, звучит следующим образом:
И здесь важно то, что плоская геометрическая фигура может быть совершенно произвольной формы.
Например, кривая, которая при вращении будет образовывать вазу или лампочку. Такие инструменты создания тел вращения очень популярны у тех, кто работает в программах 3D-проектирования.
Но с математической точки зрения, для нас, прежде всего, интересны следующие геометрические тела вращения:
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон. Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов. Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.
Шар — образован полукругом, вращающимся вокруг диаметра разреза.
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его.В обычном понимании тор — это «бублик».
Параболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком параболы. Отсюда и название параб-о-лоид. Гиперболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком гиперболы. Соответственно название гиперб-о-лоид.
Как сделать цилиндр из бумаги?
Как сделать конус из бумаги?
Как сделать параболоид из бумаги?
Как сделать гиперболоид из бумаги?
Как сделать тор из бумаги?
Для сопоставимости размеров получающихся моделей тел вращения мы постарались собрать их на одной поверхности вместе с призмами из выпуска «Волшебные грани № 16».
Получился целый математический город из бумаги, умещающийся на столе!
Определение цилиндра, формулы, свойства, типы, пример
Цилиндр — это трехмерная сплошная фигура, имеющая две параллельные круглые основания, соединенные изогнутой поверхностью на определенном расстоянии от центра. Рулоны туалетной бумаги, пластиковые банки для холодных напитков — примеры цилиндров из реальной жизни. Цилиндр имеет два основных свойства: площадь поверхности и объем. В конце 14 века слово «цилиндр» произошло от латинских (Cylindrus) и греческих (Kylindros) слов, которые означают «ролл», «ролик» и «тамблер».В этой главе мы рассмотрим формулу цилиндра, объем цилиндра, площадь поверхности цилиндра. Кроме того, вы знаете? Пизанская башня имеет цилиндрическую форму. Давайте узнаем больше о цилиндре.
Определение цилиндра
Цилиндр — это трехмерное твердое тело, состоящее из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания подобны круглому диску по форме. Линия, проходящая от центра или соединяющая центры двух круговых оснований, называется осью цилиндра.Расстояние между двумя основаниями цилиндра называется перпендикулярным расстоянием и обозначается высотой «h». Два круглых основания имеют расстояние от центра до внешней границы, которое известно как радиус цилиндра, обозначенный буквой «r». Цилиндр представляет собой комбинацию 2 кругов + 1 прямоугольник. Посмотрите на данное изображение, показывающее формирование цилиндра.
Типы цилиндров
Мы только что прочитали о некоторых реальных примерах цилиндров, которые показывают, что цилиндры могут быть разных типов.По геометрии существует четыре различных типа цилиндров. Их:
- Правый круговой цилиндр: Если ось двух параллельных линий перпендикулярна центру основания, это называется правильным круговым цилиндром.
- Наклонный цилиндр: Наклонный цилиндр — это цилиндр, стороны которого наклоняются над основанием. У наклонного цилиндра стороны не перпендикулярны центру основания. Пизанская башня — это реальный пример наклонного цилиндра.
- Эллиптический цилиндр: Цилиндр, основание которого имеет форму эллипса, называется эллиптическим цилиндром.
- Правый круговой полый цилиндр или цилиндрическая оболочка: Правый круговой полый цилиндр, также называемый «цилиндрической оболочкой», состоит из двух правильных круговых цилиндров, соединенных один внутри другого. Точка оси обычная и перпендикулярна центральному основанию. Он отличается от правого кругового цилиндра тем, что он полый по своей природе, т.е.е. внутри есть какое-то пространство или пустота.
Свойства цилиндра
Каждая геометрическая форма имеет свои особенности или некоторые свойства, отличные от других фигур. Точно так же есть несколько свойств, которые определяют цилиндр.
- По определению цилиндра, он имеет две изогнутые кромки, одну изогнутую поверхность и две плоские грани.
- Два круглых основания совпадают друг с другом.
- Размер цилиндра зависит от радиуса основания и высоты гнутого листа. Цилиндр
- называется «Правым цилиндром», если ось образует прямой угол с основаниями точно друг над другом. Цилиндр
- называется «наклонным цилиндром», ось которого не образует прямой угол с основаниями и не находится друг над другом.
- В отличие от конуса, куба или кубоида, цилиндр не имеет вершины. Это означает, что в цилиндре нет определенного угла.
- Основание и верх цилиндра идентичны, т.е.е у них одинаковое основание — круглое или эллиптическое.
Формулы цилиндра
Каждая трехмерная геометрическая фигура имеет 2 основные формулы: площадь и объем. Точно так же цилиндр имеет три основные формулы, относящиеся к площади и объему.
- Площадь боковой поверхности или криволинейной поверхности
- Общая площадь
- Том
Познакомимся с указанными формулами подробнее.
- Площадь изогнутой поверхности цилиндра: Площадь изогнутой поверхности также называется площадью боковой поверхности. Область, образованная изогнутой поверхностью цилиндра, то есть пространство, занимаемое между двумя параллельными круглыми основаниями, известна как CSA. Формула для CSA задается как площадь криволинейной поверхности (CSA) = 2πrh квадратных единиц
(Обратите внимание: «h» — высота, а «r» — радиус.) - Общая площадь цилиндра: Общая площадь цилиндра определяет общую площадь, которую он занимает.Цилиндр состоит из двух окружностей и одного изогнутого листа. Итак, чтобы узнать общую площадь поверхности цилиндра, мы вычисляем площадь криволинейной поверхности и площадь двух окружностей.
Площадь криволинейной поверхности (CSA) = окружность × высота
CSA = 2𝛑r × h
Площадь круга = 𝛑r 2
Общая площадь поверхности (TSA) = площадь криволинейной поверхности + 2 (площадь круга)
Общая площадь поверхности (TSA) = 2𝛑rh + 2𝛑r 2 = 2𝛑r (h + r) квадратных единиц.
(Обратите внимание: «h» — высота, а «r» — радиус.
Кругов два, поэтому умножаем на 2) - Объем цилиндра: Объем цилиндра определяет плотность или объем занимаемого пространства.
Объем цилиндра = Площадь круга × высота
Объем = 𝛑r 2 × h
Объем цилиндра, V = πr 2 ч куб. Ед.
(Обратите внимание: «h» — высота, а «r» — радиус.)
☛ Статьи по теме цилиндр
Посмотрите следующие страницы, посвященные цилиндру.
Часто задаваемые вопросы по цилиндру
Что такое цилиндр в геометрии?
Цилиндр — это трехмерная сплошная фигура, состоящая из двух круглых оснований, соединенных двумя параллельными линиями. Эти две параллельные линии образуют изогнутую поверхность, ограниченную двумя кругами сверху и снизу.
Каковы реальные примеры цилиндров?
Реальные примеры цилиндров: рулоны туалетной бумаги, банки, трубы, фонарики.
Каковы две основные формулы цилиндра?
Две основные формулы цилиндра:
- Общая площадь поверхности = 2πr (r + h) квадратных единиц
- Объем цилиндра = πr 2 ч куб
Сколько ребер у цилиндра?
Цилиндр имеет 2 кромки. Ребро — это место, где встречаются 2 грани. Край может быть прямым или закругленным. Например, в кубе 12 прямых кромок, а в цилиндре 2 изогнутых кромки.Мы знаем, что цилиндр представляет собой комбинацию двух кругов и одного прямоугольника. Два прямых края прямоугольника загнуты, чтобы образовать изогнутые края цилиндра.
Какова общая площадь цилиндра?
Общая площадь цилиндра — это сумма площади криволинейной поверхности и площади двух круглых оснований. Это дается как:
Общая площадь поверхности = площадь изогнутой поверхности + две круглые области основания
Общая площадь поверхности (TSA) = 2𝛑rh + 𝛑r 2 = 2𝛑r (h + r) квадратных единиц.
Что такое базовая площадь цилиндра?
Площадь, занимаемая в пределах границы круглого основания цилиндра, называется площадью основания цилиндра. Единицы площади основания цилиндра всегда выражаются в квадратных сантиметрах, квадратных дюймах, квадратных футах и т. Д. В геометрии у нас есть специальная формула для определения площади основания цилиндра, которая равна πr 2 , где r — радиус основания цилиндра.
Что вы имеете в виду под вычислителем площади цилиндра?
Калькулятор площади цилиндра — это онлайн-инструмент, который помогает вычислить площадь цилиндра для заданного радиуса и высоты в течение нескольких секунд.Попробуйте калькулятор площади цилиндра Cuemath для быстрых вычислений.
☛Также чек
Опишите свойства цилиндра.
Некоторые свойства цилиндра перечислены ниже:
- Цилиндр имеет одну изогнутую поверхность, две изогнутые кромки и две плоские круглые поверхности.
- Два плоских круглых основания совпадают друг с другом.
- Цилиндр не имеет вершины
- Основание и верх цилиндра идентичны.
- Размер цилиндра зависит от радиуса круглого основания и его высоты.
Сколько сторон у цилиндра?
В цилиндре есть две плоские круглые грани и одна криволинейная поверхность. В цилиндре мы не используем слово «стороны», так как цилиндр имеет изогнутую поверхность
20 примеров цилиндров в реальной жизни — StudiousGuy
Цилиндр — это трехмерное твердое тело, состоящее из двух параллельных круглых оснований, соединенных друг с другом с помощью изогнутой поверхности.Цилиндр, это слово произошло от латинского слова «cylindrus» и греческого слова «kylindros». Линия, проходящая из центра или соединяющая центры двух круговых оснований цилиндра, называется осью. Расстояние между круглыми основаниями цилиндра — это расстояние по перпендикуляру, которое обозначается высотой или буквой «h». Расстояние между центром основания цилиндра и внешней границей цилиндра — это радиус цилиндра, который обозначается буквой «r».
Указатель статей (Нажмите, чтобы перейти)
Типы цилиндров
По геометрии существует четыре различных типа цилиндров, а именно:
1. Круглый цилиндр правый
Если ось цилиндра перпендикулярна центру основания, это называется правым круговым цилиндром.
2. Наклонный цилиндр
Если изогнутая часть цилиндра наклоняется над основанием, то такой цилиндр называется наклонным цилиндром.В наклонном цилиндре ось цилиндра не перпендикулярна круглым основаниям. Пизанская башня — яркий пример наклонного цилиндра.
3. Эллиптический цилиндр
Как следует из названия, цилиндр, основание которого имеет форму эллипса, известен как эллиптический цилиндр.
4. Правый полый цилиндр круглой формы или цилиндрическая гильза
Правый круглый полый цилиндр или цилиндрическая оболочка состоит из двух правильных круглых цилиндров, которые закреплены один внутри другого.Точка оси обоих цилиндров общая и перпендикулярна центральному основанию. Он отличается от правильного круглого цилиндра, потому что он полый по своей природе.
Математические формулы, относящиеся к цилиндру
1. Площадь боковой поверхности цилиндра = 2πrh квадратных единиц.
2. Общая площадь цилиндра, A = 2πr (r + h) квадратных единиц.
3. Объем Цилиндра, V = πr²h куб.
здесь «r» — радиус цилиндра, а «h» — высота цилиндра.
Свойства цилиндра
Некоторые из важных свойств цилиндра следующие:
1. Основания цилиндра всегда совпадают и параллельны друг другу.
2. Если геометрическое место прямой движется параллельно на фиксированном расстоянии от оси, получается правильный круговой цилиндр.
3. Цилиндр очень похож на призму; Единственная разница в том, что он везде имеет одинаковое поперечное сечение.
Примеры цилиндров
1.Держатель для карандашей
Держатель для карандашей, который стоит наверху вашего учебного или офисного стола, является ярким примером цилиндрических объектов, присутствующих вокруг нас. Держатель карандаша обычно содержит твердое круглое основание, изогнутую поверхность, прикрепленную к окружности основания, и полую круглую вершину.
2. Консервы
Консервы или банки для холодных напитков имеют цилиндрическую форму. Следовательно, объекты цилиндрической формы можно очень легко наблюдать в нашей повседневной жизни.
3.Баллон газовый
Газовые баллоны — прекрасный пример окружающих нас предметов цилиндрической формы. Легко заметить изогнутую поверхность, соединяющую два параллельных круглых основания.
4. Ячейка
Элемент или электрохимический элемент функционирует как источник постоянного тока и используется для подачи электроэнергии на гаджеты. Обычно эти элементы изготавливаются в форме цилиндров. Следовательно, элементы, которые питают ваш пульт от телевизора, триммер, пульт переменного тока и другие предметы повседневного использования, являются классическим примером цилиндрических предметов, используемых в повседневной жизни.
5. Масляный бак
Большие металлические резервуары для хранения нефти, как правило, имеют цилиндрическую форму. Таким образом, масляные баки — еще один пример объектов цилиндрической формы, используемых в реальной жизни.
6. Карандаш
Незаточенный карандаш — еще один пример цилиндра, потому что он состоит из двух круглых и параллельных оснований, а именно, вершины и основания карандаша, а также изогнутой деревянной части.
7.Мусорный ящик
Контейнеры для пыли в основном имеют цилиндрическую форму и состоят из полого круглого верха и жесткого круглого основания.
8. Ковш
Ведро — это обычный предмет повседневной жизни, имеющий в основном форму цилиндра.
9. Чашка кофе
Кофейные чашки, стаканы, стаканы и т. Д. В основном имеют цилиндрическую форму. Таким образом, примеры цилиндрических предметов в реальной жизни можно легко увидеть, заглянув в кухонный шкафчик на кухне.
10. Полено из дерева
Бревно обычно имеет цилиндрическую форму. Также ствол дерева в основном имеет цилиндрическую форму.
11. Рулон туалетной бумаги
Рулоны туалетной бумаги имеют цилиндрическую форму.
12. Флакон духов или дезодорантов
Флаконы для духов или дезодорантов обычно имеют цилиндрическую форму; однако есть некоторые другие дизайнерские формы, в которые одеколоны упаковываются производителем.
13. Бак для воды или бутылка для воды
Резервуар для воды, который обычно устанавливается на крыше здания, обычно имеет цилиндрическую форму. Точно так же бутылки с водой являются ярким примером предметов цилиндрической формы, используемых в повседневной жизни.
14. Свеча
Свечи бывают разных форм, размеров и цветов. Одна из самых популярных геометрических фигур, которую выбирают свечники, — это цилиндр. Некоторые свечи-баночки также имеют цилиндрическую форму.
15. Дымоход
Дымоходы, устанавливаемые возле промышленных предприятий или заводов, сравнительно длиннее, чем дымоходы для дома. Это связано с тем, что высота позволяет токсичным газам выбрасываться в верхние слои атмосферы. Вы можете легко заметить, что промышленные дымоходы в основном имеют цилиндрическую форму.
16. Барабан
Малый барабан, литавра, табла, щелевой барабан, большой барабан и т. Д. — это некоторые из барабанов, которые имеют форму цилиндра.
17. Стакан
Стакан, используемый в химической лаборатории для хранения химикатов и проведения экспериментов, обычно имеет цилиндрическую форму.
18. Пробирка
Пробирки состоят из полой круглой крышки и изогнутого основания, соединенных между собой с помощью изогнутой поверхности. Следовательно, это еще один пример объектов цилиндрической формы, используемых в повседневной жизни.
19. Торт
Вкусные торты, которые используются в дни рождения и в других случаях, в основном имеют цилиндрическую форму.
20. Скв.
Колодцы также состоят из изогнутых стенок, жесткого основания и полого верха. Следовательно, колодец является ярким примером цилиндрических объектов, присутствующих вокруг нас.
Цилиндр
Цилиндр — это трехмерная геометрическая фигура с двумя одинаковыми параллельными основаниями (обычно кругами) и изогнутой поверхностью, которая «оборачивается» вокруг оснований. На рисунке ниже показаны два типа цилиндров.
Ниже приведены несколько реальных примеров цилиндров.Слева изображение цилиндрического органа. Вверху справа изображена цистерна цилиндрической формы, а справа внизу — несколько промышленных цилиндрических цистерн.
Свойства цилиндра
Цилиндр состоит из двух конгруэнтных параллельных оснований, которые обычно представляют собой окружности, и изогнутой боковой поверхности, которая пересекает основания по их периметру (окружности для круговых цилиндров).
Высота h цилиндра — это длина отрезка прямой, перпендикулярного основанию.Радиус кругового цилиндра равен радиусу его основания, как показано выше.
Любое поперечное сечение, параллельное основаниям цилиндра, образует форму, совпадающую с обоими основаниями.
Два круглых поперечных сечения круглого цилиндра показаны красным выше. Они совпадают с обоими основаниями. Это верно для любого параллельного поперечного сечения цилиндра.
Классифицирующие цилиндры
Сегмент линии, соединяющий центры оснований, может использоваться, чтобы определить, является ли цилиндр прямым или наклонным цилиндром.Отрезок, соединяющий центры двух оснований правого цилиндра, перпендикулярен обоим основаниям. Если нет, то это наклонный цилиндр. Косой цилиндр наклоняется.
Площадь правого кругового цилиндра
Площадь поверхности A правого кругового цилиндра равна
.A = 2πr 2 + 2πrh
Где r — радиус основания, а h — высота. В правой части уравнения 2πr 2 — это площадь двух оснований, а 2πrh — площадь боковой поверхности.
Если вы разрежете прямоугольный цилиндр по высоте и разложите его ровно, вы получите двухмерную сетку, как показано выше. Площадь одного круглого основания πr 2 . Высота прямоугольной боковой поверхности h. Длина такая же, как окружность оснований, или 2πr. Следовательно, площадь боковой поверхности составляет 2πrh.
Объем цилиндра
Объем V цилиндра равен площади одного из его оснований (B), умноженной на его высоту (h).
V = Bh
Для кругового цилиндра с радиусом основания r площадь основания равна πr 2 .Следовательно, объем кругового цилиндра равен
.V = πr 2 ч
Форма, значение, формула, площадь поверхности
Цилиндр: Цилиндр — это трехмерная сплошная фигура, которую можно найти в различных предметах вокруг нас, таких как газовые баллоны, свечи, железные стержни и т. Д. Здесь мы подробно обсудим свойства цилиндра. Он имеет одну изогнутую поверхность и два основания на концах.
Цилиндр можно сравнить с трубкой с двумя плоскими поверхностями.Форма цилиндра играет важную роль в нашей повседневной жизни, поскольку мы ежедневно используем множество цилиндрических предметов. Здесь мы поговорим о характеристиках, типах цилиндров и некоторых формулах, связанных с цилиндрами.
Последнее обновление:
👉 18 октября : Центральный совет среднего образования (CBSE) выпустил 10-й и 12-й листы данных CBSE по основным предметам.
👉 21 октября : CBSE выпустила 10-й и 12-й листы дат для второстепенных предметов.
Practice Embibe’s Эксклюзивные образцы документов CBSE Term 1, основанные на новых рекомендациях:
Здесь, в Embibe, вы можете получить бесплатный пробный тест CBSE Revised MCQ по всем темам. Тест MCQ, предлагаемый Embibe, основан на пересмотренных учебниках, бумажных шаблонах и учебной программе CBSE на 2021 год. Эта серия пробных тестов включает в себя исчерпывающий выбор соответствующих вопросов и их решений. Кандидаты в CBSE Board могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены.
БЕСПЛАТНО УЗНАЙТЕ КОНЦЕПЦИИ ЦИЛИНДРОВ У СПЕЦИАЛИСТОВ
Что такое цилиндр?
Цилиндр — это базовый трехмерный геометрический объект с одной криволинейной поверхностью, известной как боковая поверхность, и двумя круглыми поверхностями на концах.
Цилиндр имеет три грани, одну изогнутую грань и две плоские круглые грани, два ребра (где встречаются две грани), и у него нет вершин (углов, где встречаются два ребра), так как у него нет углов.
Каковы свойства цилиндра?
Цилиндр обладает некоторыми уникальными свойствами.
- Цилиндр имеет боковую поверхность и два основания. Общая площадь поверхности складывается из площади боковой поверхности и двух оснований.
- Основания параллельны и идентичны.
- Он похож на призму, поскольку везде имеет одинаковое поперечное сечение.
- Цилиндр может иметь два типа оснований: эллиптическое и круглое.
Какие типы цилиндров?
Существует четыре типа цилиндров.
Посмотрим, как они выглядят.
- Цилиндр круговой правый
- Наклонный цилиндр
- Эллиптический цилиндр
- Цилиндрическая оболочка или полый цилиндр
Цилиндр правый круговой
Правый круговой цилиндр — это объект, образованный вращением прямоугольника с одной из его сторон в качестве оси.
Если ось (одна из сторон прямоугольника) перпендикулярна радиусу \ (\ left (r \ right), \), то цилиндр называется правым круговым цилиндром.
Основание и верх цилиндра круглые, и они параллельны друг другу, расстояние между этими круговыми гранями цилиндра известно как высота \ (\ left (h \ right), \) цилиндра.
Наклонный цилиндр
Если круглые грани расположены не друг над другом, а сбоку, и ось образует угол, отличный от прямого, к основанию, то это называется наклонным цилиндром.
Эллиптический цилиндр
Цилиндр с основанием эллиптической формы известен как эллиптический цилиндр.
Цилиндрическая оболочка или полый цилиндр
Полый цилиндр — это цилиндр, который пуст изнутри и имеет различный радиус внешней и внутренней поверхности цилиндра. Он может иметь разные площади внутренней боковой поверхности и площади внешней боковой поверхности, поскольку внутренний и внешний радиусы не совпадают.
Некоторые примеры полого цилиндра:
Каковы примеры формы цилиндра?
Аккумулятор, железный стержень, деревянная палка для людей, свечи, бутылка с водой, газовый баллон — вот несколько примеров цилиндрической формы.
Что такое площадь?
Пространство, занимаемое плоской формой или поверхностью объекта, называется площадью. Площадь фигуры — это количество единичных квадратов, охватывающих поверхность замкнутой фигуры. Мы можем измерять площадь в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и т. Д.
Какова формула площади цилиндра?
Площадь цилиндра — это общее пространство, занимаемое цилиндром в трехмерной геометрии.Площадь цилиндра равна сумме площади боковой поверхности и площади двух круглых оснований. Между двумя круглыми основаниями имеется изогнутая или боковая поверхность. Когда криволинейная поверхность открыта, она представляет собой прямоугольную фигуру. Для определения площади цилиндра применяются различные факторы: высота, радиус, ось, сторона и основание. Радиус цилиндра считается радиусом двух круговых граней. Радиус цилиндра можно представить как \ (\ left (r \ right) \), а расстояние по перпендикуляру между двумя круговыми гранями известно как высота цилиндра.Высота цилиндра определяется как \ (\ left (h \ right) \)
Площадь поверхности цилиндра можно разделить на две части.
- Изогнутая поверхность (CSA)
- Общая площадь (TSA)
Площадь изогнутой поверхности
Площадь изогнутой поверхности называется площадью боковой поверхности. Площадь криволинейной поверхности означает площадь цилиндра без площади круглого основания.
Обычно площадь измеряется в квадратных единицах, таких как квадратный сантиметр, квадратный метр и т. Д.
Если изогнутая поверхность цилиндра открыта, то обнаруживается прямоугольная форма.
Область криволинейной поверхности включает две круглые кромки, которые могут быть такими же, как длина окружности круга.
Формула длины окружности круга равна \ (2 \ pi r. \)
Итак, можно сказать, что длина прямоугольника (после открытия изогнутой поверхности) равна \ (2 \ pi r \), а ширина равно \ (\ left (h \ right), \)
Следовательно, площадь изогнутой поверхности равна \ (2 \ pi r \ times h = 2 \ pi rh \) (поскольку площадь прямоугольника равна длине \ ( \ раз \) ширину или \ (л \ раз b \)).2} \)]
Что такое объем?
Объем — это пространство, занимаемое материей (твердым телом, жидкостью, газом или плазмой) внутри трехмерного объекта, или объем трехмерного объекта обычно определяется как емкость объекта, которая может удерживать материю.
Например:
- Песок, залитый в цилиндрическую емкость.
- Вода в цилиндрическом баке.
- Газ в цилиндрической емкости.
- Обычно объем измеряется в кубических метрах или кубических сантиметрах, а для жидкости мы используем литр.
Какова формула объема цилиндра?
Цилиндр — это трехмерное твердое тело. В общем, объем трехмерной фигуры является произведением ее площади основания и высоты.
Объем цилиндра равен произведению площади круглого основания на высоту цилиндра.
Объем цилиндра измеряется в кубических единицах.2} ч. \)
Решенные примеры — цилиндр
Вопрос 1: Радиус цилиндра \ (5 \, {\ text {cm}} \) , а высота \ (15 \, {\ text {cm}} {\ text {. 2} {\ text {h}} \) кубические единицы.2} \ times 20 \)
\ (r = \ sqrt {15.92 \,} \, = 3.99 \ приблизительно 4 \, {\ text {m}} \)
Следовательно, радиус резервуара равен \ (4 \ , {\ text {m}} \) (приблизительно).
Вопрос 5: Найдите объем цилиндрической металлической трубы, длина которой составляет \ (40 \, {\ text {cm}} \) , а внешний радиус — \ (80 \, {\ text {cm,}} \) , а толщина металлической трубы — \ (2 \, {\ text {cm}} {\ text {.}} \) Используйте \ (\ pi = 3.14 \)
Ответ: Учитывая
Длина \ (\ left (h \ right) \) металлической трубы \ (= 40 \, {\ text {cm}} \)
Внешний радиус трубы \ (= 80 \ , {\ text {cm}} \)
Внутренний радиус трубы \ (= \) Внешний радиус трубы \ (- \) Толщина металлической трубы
Внутренний радиус трубы \ (= \ left ( {80 — 2} \ right) \, {\ text {cm}} = 78 \, {\ text {cm}} \)
Мы знаем, что объем полого цилиндра \ (= \ pi \ left ({{R ^ 2} — {r ^ 2}} \ right) h \)
Теперь объем металлической трубы \ (= 3.3}. \)
Сводка
Цилиндр — это трехмерная фигура с одной криволинейной поверхностью и двумя основаниями, нулевой вершиной и двумя ребрами. Это призма с двумя основаниями. Форму цилиндра можно разделить на четыре типа: прямой круговой цилиндр, эллиптический цилиндр, наклонный цилиндр, полый цилиндр. Два основания цилиндра параллельны друг другу, а разница между двумя основаниями называется высотой или высотой.
ПРАКТИЧЕСКИЕ ВОПРОСЫ ПО ЦИЛИНДРУ
Часто задаваемые вопросы — Цилиндр
Вопрос — 1 : Для чего нужен цилиндр?
Ответ: Цилиндры используются в первую очередь для контейнеров, таких как свечи, батарейки, железные стержни и т. Д.В повседневной жизни полые цилиндры используются во многих случаях, например, в соломинках, трубках, стаканах и т. Д.
Вопрос — 2 : Что такое цилиндр и его свойства?
Ответ: Цилиндр имеет два основания и одну изогнутую поверхность.
Основания цилиндров совпадают и параллельны, и они лежат точно друг над другом. Цилиндр может иметь два типа оснований: эллиптическое и круглое.
Questio n -3: Что такое цилиндрическая форма?
Ответ: Форма цилиндра может быть найдена в различных вещах вокруг нас, таких как газовый баллон для приготовления пищи, железный стержень, свеча и т. Д.Эта форма имеет два параллельных основания и одну боковую поверхность.
Вопрос — 4 : Какие типы цилиндров?
Ответ: Есть четыре типа цилиндров: прямой круговой цилиндр, наклонный цилиндр, эллиптический цилиндр, полый цилиндр.
Вопрос — 5 : Что такое цилиндры?
Ответ: Цилиндр — это трехмерное твердое тело, имеющее два круглых основания и боковую поверхность.2} (з). \)
Учащиеся 9 класса могут воспользоваться следующими бесплатными учебными материалами от Embibe, которые определенно помогут вам в подготовке к экзамену.
Мы надеемся, что эта статья о цилиндре была полезной. Понимание формы, свойств и формул, связанных с геометрическими структурами, поможет вам решить математические задачи за доли секунды. Если у вас есть какие-либо вопросы относительно этой статьи, дайте нам знать об этом в разделе комментариев ниже.Мы свяжемся с вами в ближайшее время.
538 просмотров
трехмерных фигур | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) — это твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.
См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые кромки .
- Плоские стороны называются гранями .
- Углы, называемые вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках). Многогранники также могут быть вогнутыми или выпуклыми.
Один из самых простых и известных многогранников — это куб.Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных тел. — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник. Платоновы тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
Каждый из этих правильных многогранников показан на диаграмме выше.
Что такое призма?
Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы.Стороны призмы составляют параллелограммов — четырехугольные формы с двумя парами сторон равной длины.
Антипризмы похожи на обычные призмы в том, что их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре ее основания, правая пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Есть еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. Шесть граней — правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с закругленными или закругленными краями не являются многогранниками.Многогранники могут иметь только прямые стороны. Также см. Нашу страницу о двумерных изогнутых формах.
Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого.Цилиндры имеют два одинаковых конца в форме круга или овала. Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или земного шара, представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Обычный кольцевой тор в форме кольца, шины или бублика образуется путем вращения меньшего круга вокруг большего круга. Существуют также более сложные формы торов. |
Площадь
На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы, чтобы рассчитать площадь поверхности трехмерных фигур.
Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двумерных фигур для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы прорабатываете площадь каждой грани, а затем складываете их вместе.
Как и в случае плоских форм, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба 10 × 10 см = 100 см 2 .Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба составляет 600 см 2 .
Другие правильные многогранники
Аналогично, площадь поверхности других правильных многогранников (платоновых тел) может быть вычислена, если найти площадь одной стороны и затем умножить ответ на общее количество сторон — см. Диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь всех четырех сторон, или
Умножьте свой ответ на 2.
Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы вычислить площадь поверхности других типов пирамиды, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковой поверхности). Возможно, вам придется измерить стороны индивидуально.
Диаграммы сети
Геометрическая сеть — это двухмерный «узор» для трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о сетевых диаграммах см. Нашу страницу 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два конца одинаковые и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и приплюснуть, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.
Сначала проработайте область одного из кругов.
Площадь круга π (пи) × радиус 2 .
Предполагая радиус 5 см, площадь одного из кругов составляет 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как есть два круга 157см 2
Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см 2 .
Общую площадь поверхности можно определить, сложив вместе площадь кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «склона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга у основания конуса равна π (пи) × радиус 2 .
В этом примере расчет: 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь боковой части, наклонного участка, может быть найдена по следующей формуле:
π (пи) × радиус × длина уклона.
В нашем примере расчет составляет 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к боковой области, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто легче измерить диаметр — расстояние по сфере.Затем вы можете найти радиус, равный половине диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам понадобится радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь теннисного мяча составляет:
.4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаковый для каждой детали.
Формула: площадь поверхности = (2πR) (2πr)
Для определения площади поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Умножьте два ответа вместе, чтобы найти общую площадь поверхности тора в примере.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Хотите ли вы освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Заполнение твердого тела: Том
Для трехмерных фигур вам также может потребоваться знать, какой объем у них есть.
Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Что такое цилиндры? Как рассчитать их площадь и объем
Вы знаете, что такое цилиндр? Помимо объяснения того, что такое цилиндры, в этом посте мы рассмотрим, как они развиваются, из каких частей состоит цилиндр и как рассчитать его площадь и объем. Мы также покажем вам некоторые упражнения с использованием цилиндров, которые дети выполняют во время занятий Smartick.
Что такое цилиндр?
Цилиндр — это геометрическое тело , которое образовано прямоугольником, который вращается вокруг одной стороны .В математике это также определяется как цилиндрическая поверхность, которая образуется, когда параллельная линия вращается вокруг другой параллельной линии, которую мы называем осью.
Чтобы прояснить это понятие, следует иметь в виду, что речь идет о твердом цилиндре, то есть геометрическом теле. Мы называем поверхность цилиндра полым цилиндром . Вот пример:
Расчеты, которые мы сделаем в этом посте, относятся к твердым цилиндрам .
Типы цилиндров
Есть два типа цилиндров :
Прямоугольный цилиндр
Когда ось цилиндра перпендикулярна основанию.
Наклонный цилиндр
Если ось не перпендикулярна основанию.
Свеча — это пример прямоугольного цилиндра, а стопка монет — пример наклонного цилиндра. Как изобразить развитие поверхности цилиндра?Развитие геометрического тела заключается в том, чтобы видеть всю его поверхность на плоскости, в данном случае — поверхность твердого цилиндра.Но будь осторожен! Вам нужно убедиться, что у него есть основания, потому что, например, если вы «развернете» рулон туалетной бумаги, у вас будет только прямоугольник.
Развертка цилиндра состоит из прямоугольника , который представляет собой боковую часть цилиндра, и двух окружностей , которые являются его основаниями. Если хотите, можете прочитать этот пост о геометрических фигурах, чтобы запомнить основные характеристики прямоугольников и кругов.
Какие характеристики имеют цилиндры?
Когда мы создаем цилиндр, вращая прямоугольник:
- Ось — это сторона прямоугольника, которая остается неподвижной при повороте.
- Основания представляют собой две окружности, перпендикулярные оси. Это крышки, закрывающие цилиндр.
- Высота — это расстояние между основаниями.
- Радиус (r) — это длина от оси до края цилиндра, соответствующая радиусу основания.
Как рассчитать площадь цилиндра?
Вы должны рассмотреть развертку цилиндра и вычислить площадь его частей, прямоугольника и двух оснований .
Площадь прямоугольника = 2 × π × r × h
Площадь основания = π × r 2 (Помните, что у него два основания!)
Сложив все, мы получим площадь = 2 × π × r × h + 2 × π × r 2
Площадь = 2 × π × r × (h + r)
Пример площади цилиндра
- Вычислите площадь цилиндра радиусом 3 см и высотой 6 мм.
Во-первых, мы должны убедиться, что для радиуса и высоты используются одинаковые типы измерений, поэтому нам нужно преобразовать измерение высоты из миллиметров в сантиметры. Если хотите, можете просмотреть этот пост об измерениях длины, чтобы освежить свою память.
60 мм = 6 см
Теперь мы собираемся вычислить площадь прямоугольника , которая эквивалентна боковой поверхности цилиндра. Как мы указали в формуле ранее, мы просто подставляем значения цилиндра:
Площадь прямоугольника = 2 × π × r × h
2 × 3.14 × 3 × 6 = 113,04 см²
Нам также нужно вычислить площадь оснований , которая равна основанию, но умножена на 2. Мы используем формулу, которая была дана нам ранее, и подставляем значения:
Площадь оснований = 2 × π × r 2
2 × 3,14 × 9 = 56,52 см²
И, наконец, складываем части цилиндра, боковую площадь, которая является площадью прямоугольника, и площадь оснований:
Площадь цилиндра = 2 × π × r × h + 2 × π × r 2
113.04 + 56,52 = 169,56 см²
Как рассчитать объем цилиндра?
Объем равен площади основания, умноженной на высоту, помните, что мы указываем высоту буквой «h».
Объем = π × r 2 × h
Пример объема цилиндра
- Вычислите объем цилиндра радиусом 5 см и высотой 60 мм.
Как указано выше, мы должны использовать одну и ту же единицу измерения и для радиуса, и для высоты.Нам нужно преобразовать высоту из миллиметров в сантиметры:
60 мм = 6 см
Чтобы вычислить площадь основания, умножим π на квадрат радиуса:
Площадь основания = π × r 2
3,14 × 25 = 78,50 см²
Чтобы найти объем цилиндра, нам нужно умножить площадь основания на 6 см, что составляет высоту:
78,50 × 6 = 471 см³
Чтобы вычислить этот объем, мы умножили площадь (квадратные единицы) на высоту (линейные единицы), так что в результате мы получили кубические единицы.Помните, что единицей измерения объема в Международной системе единиц является кубических метров и (м³), хотя мы использовали см³, что является его долей.
То, что мы вычислили, применимо независимо от того, является ли цилиндр прямым или наклонным цилиндром . Подумайте об этом, если бы это было похоже на башню для монет, которую мы представляли как наклонную башню, если бы мы сделали ее прямой, она имела бы такой же объем.
Примеры упражнений на определение геометрических фигур в Smartick
В продолжение, мы рассмотрим различные типы упражнений, которые есть в Smartick, чтобы научиться определять цилиндр.
Определение геометрических фигур
Определение геометрических фигур на изображении
Появляется геометрическая фигура, и ребенок должен идентифицировать и выбрать ее имя из различных предложенных вариантов.
Сравнение цилиндра с реальными объектамиРебенок должен определить, какой реальный предмет из представленных напоминает цилиндр. В качестве наглядной поддержки им представлено геометрическое тело.
Как определить, похож ли реальный объект на цилиндр
Определение названия геометрической фигуры, похожей на реальный объект
Ребенку дарят предмет из повседневной жизни, и ему нужно выбрать его имя среди предложенных вариантов.
Это всего лишь несколько примеров деятельности Smartick. Если вы хотите узнать больше, зарегистрируйтесь в Smartick и попробуйте наш онлайн-метод бесплатно.
Подробнее:
Развлечение — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 веселых минут в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Конус, цилиндр и полусфера
Конус, цилиндр и полусфераМагазин не будет работать корректно, если куки отключены.
Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.
- Дом
- Геометрические формы (конус, цилиндр и полусфера), заполняемые
Высокое качество, полусфера, цилиндр и конус, объемные модели; Высота: 60 мм; Диаметр: 120 мм.Отличный инструмент для математического класса! Практичный инструмент, который поможет ученикам увидеть и почувствовать основные геометрические формы. Сделано в Германии.
62,99 доллара США
Доступность: Распродано
Высокое качество, полусфера, цилиндр и конус, объемные модели; Высота: 60 мм; Диаметр: 120 мм.Отличный инструмент для математического класса! Практичный инструмент, который поможет ученикам увидеть и почувствовать основные геометрические формы. Сделано в Германии.
- Модели объема конуса, цилиндра и полусферы
- Отличный интерактивный инструмент для учебы!
| Страна производитель | Германия |
|---|---|
| Материал | Пластик |
| Размеры продукта | диаметр 120 мм |
| Безопасность | Нет опасности дросселирования |
| UPC | 652012000860 |
об обновлениях и акциях
×
.
 Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
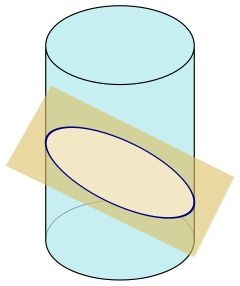 Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.