Как начертить ровную звезду: Рисуем Звезду (с разными вершинами)

Нарисовать ёлку карандашом. Пошаговая инструкция «Шаг за шагом» как рисовать Новогоднюю ёлочку. Самый простой способ

Нарисовать самостоятельно елку просто. Выполните описанные в статье этапы, чтобы создать настоящий новогодний шедевр.

Любимый праздник всех детей и взрослых — это Новый год. С наступлением зимы, мы готовимся к его встрече: закупаем сверкающие украшения для дома, гирлянды и разноцветные фонарики.

• Главный атрибут этого праздника — елка
• Многие люди принципиально не покупают живые ели из своих побуждений, а другие хотят, чтобы природа осталась нетронутой для наших потомков
• Искусственные елки стоят дорого, поэтому необходимо научиться рисовать это вечнозеленое дерево, чтобы украсить свой дом, и создать новогоднее настроение в нем
• Сделать своими руками атрибут новогоднего праздника просто, нужно только запастись терпением и красками

Как нарисовать елку поэтапно карандашом?

Приготовьте большой лист бумаги, ведь елка — это дерево, и она должна быть высокой.

Минимальный размер листа, на котором нужно изобразить новогодний атрибут — это формат А1. Можно склеить несколько таких листов, и тогда получится настоящий шедевр.

Как нарисовать елку поэтапно карандашом:

• Посередине листа проведите ровную линию карандашом
• В самом верху этой линии нарисуйте звезду , как на картинке выше. Можно нарисовать ровную пятиконечную звездочку . Все зависит от вашей фантазии
• От звезды вниз проведите две линии , но не ровные, а плавно расходящиеся в стороны. Соедините их зигзагообразной полосой
• Ниже нарисуйте еще одну такую деталь , которая будет начинаться уже от второго зигзага с правой и левой стороны. Она должна получиться чуть больше верхней части
• Самую последнюю — третью часть елки , нарисуйте еще больше по размеру, чем вторую. В самом низу у новогодней красавицы изобразите ствол
• Раскрасьте ель зеленой краской
  : верхняя деталь — светлым, а вторую и третью — темными оттенками
• Нарисуйте елочные игрушки разными цветами, и фон со снегом

Совет: Такое изображение новогоднего атрибута можно повесить на стену в гостиной или в детской комнате. Украсьте картину мишурой и разноцветным блестящим дождиком.

Рисуем елку поэтапно по клеточкам для детей

Детям легче объяснить, как правильно изображать елку на тетрадном листе с клеточками. Когда ребенок поймет, что ель — это несколько треугольников разной величины , он сможет рисовать ее на простом листе, без клеточек.

Такие рисунки в детском саду называются графическими диктантами . Они помогают подготовить малышей 5-7 лет к школе. Эти уроки учат ребенка быть внимательным, слушать преподавателя и выполнять то, что он говорит.

Совет: Занимайтесь с вашим крохой дома при помощи графических диктантов, и малышу будет легче учиться в школе.

Итак, этапы рисования елки по клеточкам для детей:

Рисуем елку поэтапно по клеточкам для детей

• Положите перед ребенком тетрадный лист в клетку и карандаш или ручку
• Скажите ему, чтобы он отступил 10 клеток слева, 3 клетки сверху, поставил точку и начал рисовать.
• Теперь диктуйте по схеме , по столбикам: 1 клетку влево, 2 клетки вниз, 1 клетку влево, 1 клетку вниз и так далее.
• Когда ребенок дорисует до низа листа , проведите линию-симметрию, и попросите малыша нарисовать тоже самое, но с другой стороны, как отображение в зеркале.
• Рисунок закончен , спросите у ребенка: что получилось?

Важно: Таким образом можно рисовать разные предметы и животных. Главное, работайте с малышом в игровой форме. Например, во время рисования, прочитайте стих про елку или вместе с ним пойте песню.

Нарисовать ель может понадобиться ребенку в школе или даже его родителям — на работе или дома, в особенности, перед новогодними праздниками.

Важно: Главное, при изображении любого предмета на бумаге — это его схематический рисунок карандашом — набросок. Когда все этапы в карандаше будут выполнены, можно приступать к раскрашиванию красками.

Рисование ели карандашом поэтапно:

• Нарисуйте прямую вертикальную линию такой длины, какая будет по высоте елка.
• Отступите немного от верха и начертите плавно изогнутые линии в стороны от вертикальной полосы — это заготовки для рисования ветвей.
• Теперь нарисуйте макушку , как показано на рисунке, и «мохнатые лапы» или ветви дерева, обрисовывая каждую линию-заготовку.
• Одну такую «лапку» изобразите посередине . На земле можно нарисовать снег или траву.
• Если нужно, раскрасьте дерево красками . Все — рисунок готов.

Легкие рисунки елки для срисовывания

Если у вас не получается самостоятельно нарисовать ель, тогда обведите готовый рисунок, приложив его к окну вместе с чистым листом бумаги, или срисуйте елку другим образом на столе.

Совет: Распечатайте готовые изображения на принтере и создайте свой неповторимый шедевр.

Легкие рисунки елки для срисовывания:

Миниатюрная ель в ведре. Проявите фантазию и разукрасьте ее красками или фломастерами.

Легкие рисунки елки для срисовывания

Рисунок большой ели. На нее можно повесить много разноцветных шаров и гирлянд.

Легкие рисунки новогодней елки для срисовывания

Эскизы оригинальных елочек, которые можно увеличить и нарисовать на большом листе бумаги.

Легкие рисунки елок для срисовывания

Учитесь рисовать в любом возрасте. Это всегда пригодится в жизни. Кроме этого такое занятие успокаивает нервную систему и добавляет позитива в наши серые будни.

Видео: Учимся рисовать елочку

Для него на бумаге создается канва в виде треугольника, форма которого позволит в результате получить елку с симметричными сторонами и желаемого размера. Для этого можно использовать линейку или обычный треугольник, с которым нарисовать аккуратные линии даже проще.

Верх треугольника станет макушкой елки, ветви которой могут иметь как четкие линии, так и имитировать иголки, если линии рисунка создаются не прямыми, а в форме зубчатых вырезов. По мере расширения сторон треугольника более массивными становятся и ветки елки.

Нижняя часть рисунка может заканчиваться изображением ствола дерева или просто снега, в котором утопают раскинувшиеся ветки новогодней красавицы.

Если присутствуют сомнения в том, что удастся сделать ветки одинаковыми по размеру, то внутри самого треугольника можно провести тонкие горизонтальные линии, которые будут служить границей между ветками елки, позволяя получить их симметричными. По такой схеме трудностей с тем, как нарисовать ёлку поэтапно карандашом, легко и красиво и за считанные минуты, не возникнет при любом уровне профессионализма и художественных навыков.

Интересно! В данной технике карандаш может стать не единственно возможным инструментом. С таким же успехом базовая часть елки может быть обведена фломастерами, а закрашена красками. Оригинальной помогут сделать елку и объемные аппликации, когда поверх уже готового рисунка игрушки и гирлянды не рисуются, а приклеиваются из иных материалов. Вы уже знаете, ?

Второй способ рисования елки легко и красиво

Для того чтобы им воспользоваться и выяснить, как нарисовать ёлку поэтапно карандашом, легко и красиво, используется несколько иной шаблон, чем тот, что описан выше. Треугольник заменяется вертикальной линией, обозначающей высоту будущего деревца. Регулировать размеры таким методом очень легко: чем выше линия, тем больше сама ель.

Начнется рисунок с изображения звезды, венчающей макушку и одновременно выступающей в качестве верхушки дерева. Всего у елки будет три уровня, верхний из них в форме треугольника рисуется непосредственно под звездой. Зубчатые концы нижней линии треугольника имитируют ветки. Желательно делать их не совсем прямыми, а с легким изгибом в форме полумесяца, выступающая часть которого будет направлена вниз.

Второй треугольник рисуется больше и шире первого, так как елка расширяется от макушки вниз, к нижней части ствола. Самый большой треугольник последний. Зубчики на нем должны присутствовать также, как и на всех остальных, иначе рисунок будет в большей степени схематичным и не напоминающим реальную пушистую красавицу. Также мы рассказываем, Собаки по знакам зодиака.

Последний шаг — это нарисовать ствол дерева, сделать который ровным и не ошибиться с центром помогает все та же вертикальная линия. Украсить ель можно по своему вкусу и фантазии.

Рисуем елку: рисование елки фломастерами с детьми

Мастер-класс проводит Вера Парфентьева — читательница сайта «Родная тропинка», учитель технологии, руководитель кружка детского творчества, участница нашей Интернет-Мастерской развивающих игр «Через игру — к успеху!».

Предложите ребенку нарисовать в подарок другу, близким, родным новогоднюю открытку с нарядными елочками, с шариками, бусами, красивыми игрушками!

Перед рисованием рассмотрите с ребенком елочку на картинке: у нее есть ствол (какого он цвета, формы), есть зеленые пушистые колючие ветви. Крона елки колючая, с иголками, по форме похожа на треугольник: внизу она широкая, а вверху на макушке елки — узкая. Ветви идут не с самого низа елки, а начинаются чуть повыше, поэтому внизу у земли мы видим ствол елочки.

Рисуем елку с детьми фломастерами: материалы и инструменты

Для работы необходимо:

— белый альбомный лист,

— фломастеры,

— простой карандаш,

— линейка.

Рисуем елку с детьми фломастерами: пошаговое описание

При рисовании елки этим способом с маленькими детьми дайте ребенку готовый шаблон. Пусть он его обведет (вместо шага 1 и шага 2).

Шаг 1

Согнуть альбомный лист пополам. В центре начертить равнобедренный треугольник.

Для этого в центре открытки провести тонкую вертикальную линию, еле видимую глазу. В верхней части линии поставить точку – вершину треугольника. В нижней части открытки провести горизонталь, на которой от тонкой линии влево и вправо отложить равные отрезки, например по 4 см. Соединить их концы с вершиной. Таким образом, получим равнобедренный треугольник, т.е. треугольник, у которого две стороны равны между собой с основанием 8 см.

Шаг 2

Начертить под елочкой прямоугольник или квадрат по своему выбору, также ориентируясь от центральной тонкой линии – это ствол елочки.

Шаг 3

На заднем плане за ёлочкой начертить еще два треугольника.

Шаг 4

А теперь начинается самая интересная работа! Нужно пофантазировать и придумать для елочек наряды. В статье мы даем примеры нарядов для елок, Вы можете придумать другие наряды елки.

Центральную елочку разделим наклонными полосами. В результате получим вот такие ячейки.

Шаг 5

Отобрать фломастеры зеленых оттенков и закрасить полученные ячейки зелеными фломастерами двух оттенков в шахматном порядке.

А можно вначале на белом фоне в каждой ячейке нарисовать, например, шары, бусы яркими фломастерами, а потом оставшиеся места в ячейках закрасить зеленым цветом. Этот вариант испытаем на следующем шаге.

Шаг 6

На одной ёлочке нарисуем круги разных размеров. А на другой – волнистые линии, идущие сверху вниз.

Шаг 7

Раскрасить круги по вашему замыслу. А пространство в треугольнике между кругами закрасить зеленым фломастером другого оттенка, чтобы елочка эта не сливалась с первой.

Шаг 8

Волнистые линии раскрасить зелеными фломастерами разных оттенков. Между линиями нарисовать круги, ромбики, звездочками – всё, что вам подскажет ваша фантазия.

Шаг 9

Закрасить расстояние между волнистыми линиями разными оттенками зелёного цвета. Закрасить ствол коричневыми фломастерами 2 – 3-х оттенков. Линии рисуем сверху вниз. Украсить центральную елочку как подскажет фантазия. А можно приклеить разноцветные пайетки.

Наша открытка готова! Любуемся красотой и кладем открытку в коробочку для подарков к Новому году! Такие наряды для елок придумала семилетняя Настя.

Творческое задание:

— Какие техники можно применить для оформления подобной открытки?

— Нарисуйте треугольные ёлочки и раскрасьте их красками или карандашами. А можно сочетать сразу несколько способов, например, краски с фломастерами, или мелками или все способы вместе. Фантазируйте!

— Выполните треугольные ёлочки в технике аппликации из цветной бумаги и украсьте их пайетками, бусинками, бисером, стразами. Как сделать оригинальную аппликацию треугольной елочки для открытки Вы узнаете из статьи .

— Выучите с ребенком стихи о елке к новогоднему празднику. Подборку из 38 стихов о елке для детей от 2 лет до 7 лет Вы найдете в статье .

Удачи вам в творчестве!!!

Рисуем елку: способы рисования елки красками и карандашами

Способов изображения елки очень много. Ниже в картинках вы увидите некоторые из них. Но вы можете придумать и свой способ на основе данных ниже таблиц и картинок. Фантазируйте, пробуйте, не бойтесь экспериментировать! Придумывайте, какого характера будет Ваша елка, как Вы отразите это в линии, в ее форме, цвете.

Рисуем елку красками и карандашами: первый способ рисования

Рисуем елку красками и карандашами: второй способ рисования

Сейчас мы рассмотрим, как нарисовать новогоднюю елку в трех вариантах карандашом поэтапно.

Сначала попробуйте нарисовать эту елочку, если будет сложно внизу два легких варианта.

Нарисуйте оставшуюся часть, сотрите вспомогательный треугольник.

Рисуем часть ствола и ведро(горшок), где елка стоит.

Елка у нас же новогодняя, значит нужно ее украсить гирляндой и новогодними игрушками.

Разукрашиваем.

Ниже рассмотрены 2 простых варианта.

Новогодняя елочка прекрасна и светиться огоньками. Мы так любим ее наряжать на Новый год. Красивые гирлянды вешаем на нее, новогодние игрушки, звезду устанавливаем на самом верху. А под низом, когда мы проснулись после Нового года нас ждет много-много подарков под елкой. Новогодняя елка — это символ Нового года и неотъемлемый атрибут, который стоит в каждом доме, квартире, семье. Елки стоят дома натуральные и искусственные. На праздник Новый год елка должна быть нарядная, поэтому наряжают ее всей семьей, потому что она большая. Натуральная новогодняя елка приятно пахнет и освежает воздух дома. Также покупаем маленькие веточки елки и украшаем их. При рисовании новогодней елки главное правильно установить ее центр и от него разводить в сторону линии влево и вправо, показывая ее ветви. Затем показываем пушистость волнистыми линиями снизу и снова разводим в сторону линии, и так далее. Затем нужно внизу показать ствол елки и нарисовать много игрушек. Вот и все у вас все получилось. А вы целый день думали: «Как нарисовать елку?».. Смотрите еще много уроков рисования про Новый год.

До Нового года осталось чуть меньше месяца, мы готовим подарки и рисуем открытки. А вы? Если да, то две новогодние елочки ждут вас в этом уроке. Любители рукодельничать перед праздниками чувствуют особое воодушевление, ведь свои творческие порывы можно направить в изготовление подарков и открыток. Открытки, сделанные своими руками, пусть даже самые простые, вызывают очень теплые чувства у близких людей. А уж как бабушки восторгаются творениями своих внуков!

Я не буду рассказывать, как сделать саму открытку, а покажу как нарисовать новогоднюю елочку для открытки. Точнее, даже 2 новогодние елочки. Они обе достаточно простые, их можно рисовать и взрослым, и детям.

В первом случае конструкция елочки более простая и понятная для детей, а украшательства можно усложнять. Можно разукрасить елочки в новомодном стиле , как это сделала я, или как-то по своему.

Ёлочка серебристая

Серебристая она потому, что на открытке я рисовала серебристыми маркерами и контуром. Но об этом чуть позже.

Для рисования я не использовала карандаш. Посмотрите на схему, чтобы понять, как нарисовать елочку поэтапно. Прежде, чем рисовать на открытке можете потренироваться порисовать карандашом или маркером. В моем случае синяя тренировочная елочка выполнена обычным тонким маркером.

На схеме каждый новый шаг отмечен красным цветом.

1. Для четырех ярусов надо наметить 5 точек –разделителей вертикально посередине будущей елочки. Не забывайте сверху и снизу оставить свободное место. Если на макушке планируете нарисовать высокий наконечник, то оставьте места побольше.
2. Представьте, как от верхней точки вниз расширяются линии, образуя треугольник. Кстати, если вам удобнее сделать предварительную границу елочки, то наметьте треугольник карандашом. Рисуем верхний ярус но не треугольником, а как колокольчик, немного загибая уголки основания вверх и опуская нижнюю границу по центру дугой.
3. — 5. Остальные ярусы рисуем как юбочки, так же поднимая уголки и опуская дугой нижнюю границу. 6. Осталось нарисовать наконечник и ножку (по желанию).

Вот и готова наша форма, которую теперь можно наполнять разными узорами. Мои елочки наполнены разными дудлами — кружочками, завитками, цветами, в свободной форме, несимметрично. А вокруг я нарисовала завитки и снежки для большей нарядности.

Елочка в стиле дудларт выполнена тонкими маркерами двух цветов

Как нарисовать новогоднюю елочку в простом варианте вы теперь знаете.

Такую елочку с удовольствием рисуют и дети. Им можно предложить нарисовать елочку цветными фломастерами или карандашами. Конечно, в этом случае нужно прорисовать все «юбочки» простым карандашом, и только потом приступать к раскрашиванию. В рубрике Зенарт и графика есть готовые раскраски новогодних ёлочек для детей разного возраста, а также шаблоны-раскраски елочек в стиле дудлинг.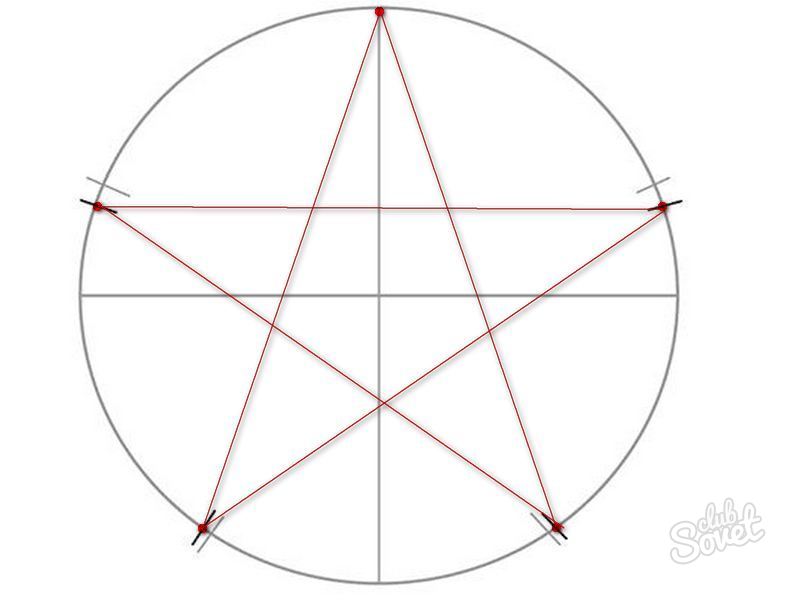 А вот что получилось у нас.

детский рисунок по этому уроку

Открытка с серебристой елочкой в стиле дудларт

Теперь расскажу об открытке. Я взяла темную плотную бумагу с красивой фактурой из альбома. Наметила размер открытки и вырезала. Темная бумага немного капризная. Поэтому перед рисованием я помыла и высушила руки, чтобы не оставить от рук отпечатки, подложила под руку лист. Наметила точки карандашом, а затем и белым маркером. Границы елочки я не прорисовывала, поскольку от стирания ластиком карандаша остаются следы на бумаге, которые портят весь вид.

Далее белым маркером (здесь фирмы ZIG) нарисовала юбочки. Наполнила их серебристыми узорами, сделанными гелевой ручкой. И добавила еще несколько спецэффектов, которые, к сожалению, не очень видны на фото: некоторые детали я украсила мелкодисперсными голографическими блестками, а также добавила точки серебристым объемным контуром.

Открытка получилась стильная и нарядная. Внутри я украсила уголок узором в том же стиле, серебристой гелевой ручкой. Наклеила квадратик плотной светлой бумаги — это место для написания поздравления.

А теперь обещанный второй урок – как нарисовать елочку поэтапно, но в другом варианте.

Ёлочка зеленая

Эта елочка может показаться немного сложнее, поэтому также советую для начала несколько раз накидать эскиз карандашом в уменьшенном варианте, чтобы потом легко нарисовать на открытке. Ведь, как вы поняли, на открытке лучше делать как можно меньше подтирок и разметок, тогда бумага не портится, и рисунок выглядит аккуратнее. Но в этом варианте без карандаша обойтись сложнее. На карандашную разметку я положила контуры маркером, а перед раскрашиванием елочки стерла видимые части карандашного эскиза.

1. Рисуем конус карандашом. Любите пользоваться линейкой? Пожалуйста, можете использовать линейку – уголок.
2. Карандашом же рисуем полоски.
3. Прежде, чем рисовать саму елочку, можете уже маркером нарисовать наконечник, он закроет самую макушку.
4. Теперь делаем контуры ярусов елочки маркером, и стираем карандашный эскиз, там, где его видно. Если вы рисуете гелевой ручкой, дайте ей просохнуть, прежде чем будете стирать карандаш.
5. Рисуем контуры елочных украшений, например, цветными маркерами или карандашами.
6. Заполняем пространство между игрушками зеленым цветом, также фломастерами, маркерами или карандашами.

Ленты не раскрашиваем, это декоративный эффект. Как нарисовать новогоднюю елочку, чтобы она была праздничной, нарядной? Добавьте сияния! Вот такая получилась елочка у нас.

Мы взяли желтый односторонний картон, на котором нарисовали елочки, некоторые контуры обвели серебристой и золотистой гелевыми ручками, поэтому украшения красиво играют на свету. Особенно красивое мерцание при искусственном освещении. Также можно использовать гели с блестками для детского творчества.

В дальнейшем мы вырезали прямоугольник с елочкой и вклеили его на открытку из декоративной бумаги. Кстати, елочку можно нарисовать на самоклеющейся бумаге, чтобы потом также приклеить на заготовку для открытки.

На сегодня все! Если вам понравилось, оставьте отзыв в комментах. Напоминаю, что ваши творения вы можете отправлять в ленту нашего клуба во Вконтакте vk.com/zenarts

Построение правильного пятиугольника с помощью циркуля. Как нарисовать звезду с помощью линейки быстро? Получение с помощью полоски бумаги

Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.

Разновидности звезд

Существует множество вариантов внешнего вида такой фигуры, как звезда.

Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.

Существуют также шестиконечные, хвостатые кометы.

Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.

В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.

Выполнение чертежа

Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.

Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.

Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.

Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.

Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе.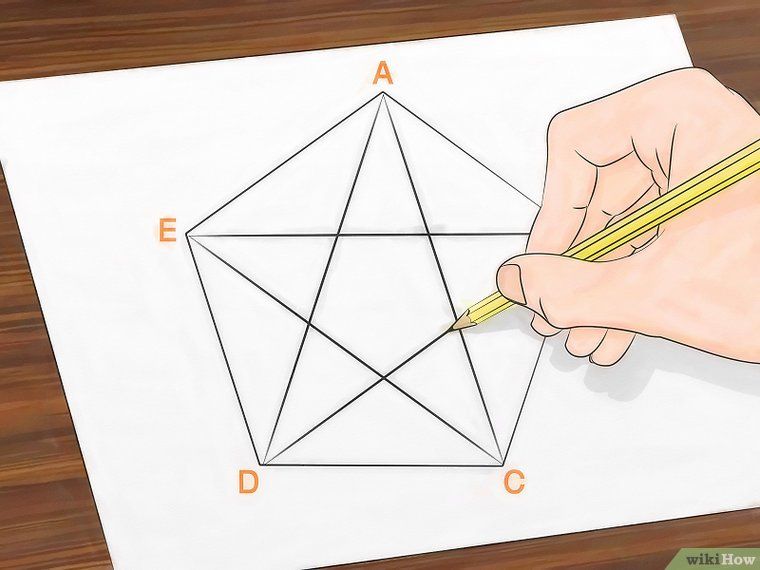 Но самое главное — это логическое мышление.

Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.

Классическая техника

Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.

Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.

Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.

Можно в работе воспользоваться специальными вычислениями.

Расчет фигуры

На этом этапе рисования правильной звезды проступают контуры готовой фигуры.

Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.

Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.

Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.

Оформление работы

Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.

Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.

Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.

Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.

Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.

По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.

Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.

Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!

5. 3. Золотой пятиугольник; построение Евклида.

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).

Для построения пентаграммы необходимо построить правильный пятиугольник.

Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».

Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника

из центра описанной окружности. Начнем с

отрезка АВЕ, разделенного в среднем и

Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,

180=(3a -180) + (3a-180) + (180 — a)

Откуда 5a=360, значит a=72.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.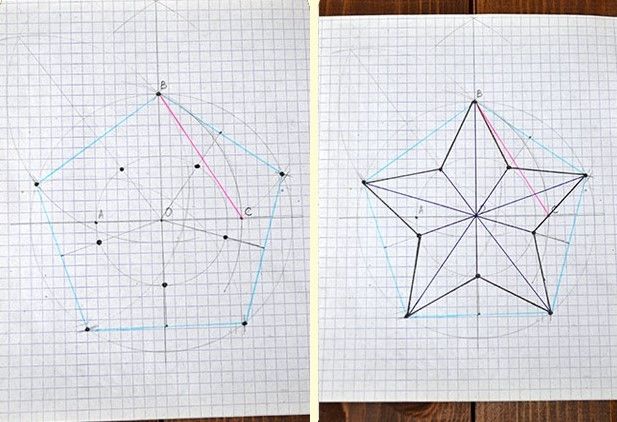

Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:

CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)

Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2

Итак, АС = jа = jАВ = АЕ, что и требовалось доказать

5.4.Спираль Архимеда.

Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

В настоящее время спираль Архимеда широко используется в технике.

6.Числа Фибоначчи.

С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)

В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

Рассмотрим одну такую задачу:

«Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Пары кроликов	2	3	5	8	13	21	34	55	89	144	233	377

Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:

u 1 , u 2 … u n

в которой каждый член равен сумме двух предыдущих, т.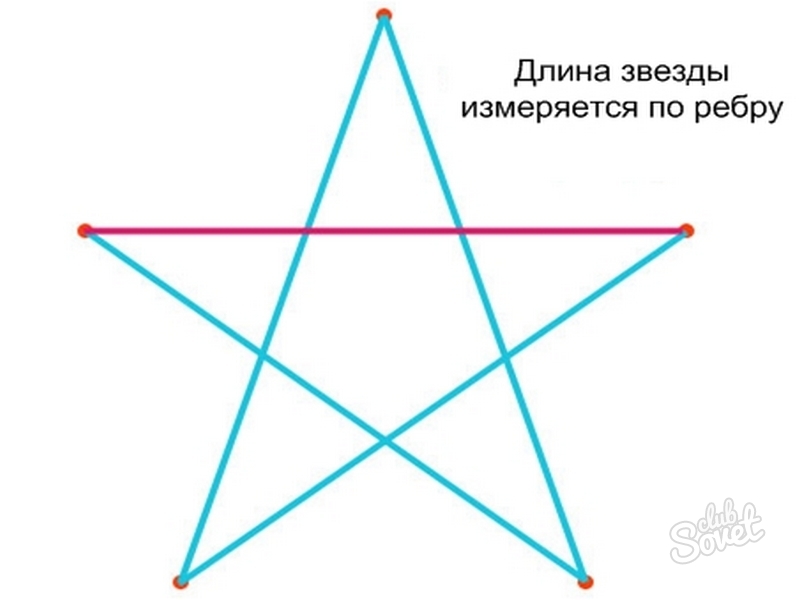 е. при всяком n>2

u n =u n -1 +u n -2 .

Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше фи на 0.6180

2:1 = 2. 0000, что больше фи на 0.3820

3:2 = 1.5000, что меньше фи на 0.1180

5:3 = 1.6667, что больше фи на 0.0486

8:5 = 1.6000, что меньше фи на 0.0180

По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.

Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.

Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0.382

Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.

Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.

Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.

Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.

Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.

7.Золотое сечение в искусстве.

7.1. Золотое сечение в живописи.

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..

Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.

В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.

7.2. Пирамиды золотого сечения.

Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича

8. Заключение.

Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.

Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.

Раковина наутилуса закручена подобно золотой спирали.

Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.

Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.

На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.

Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».

Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»

Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.

Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами.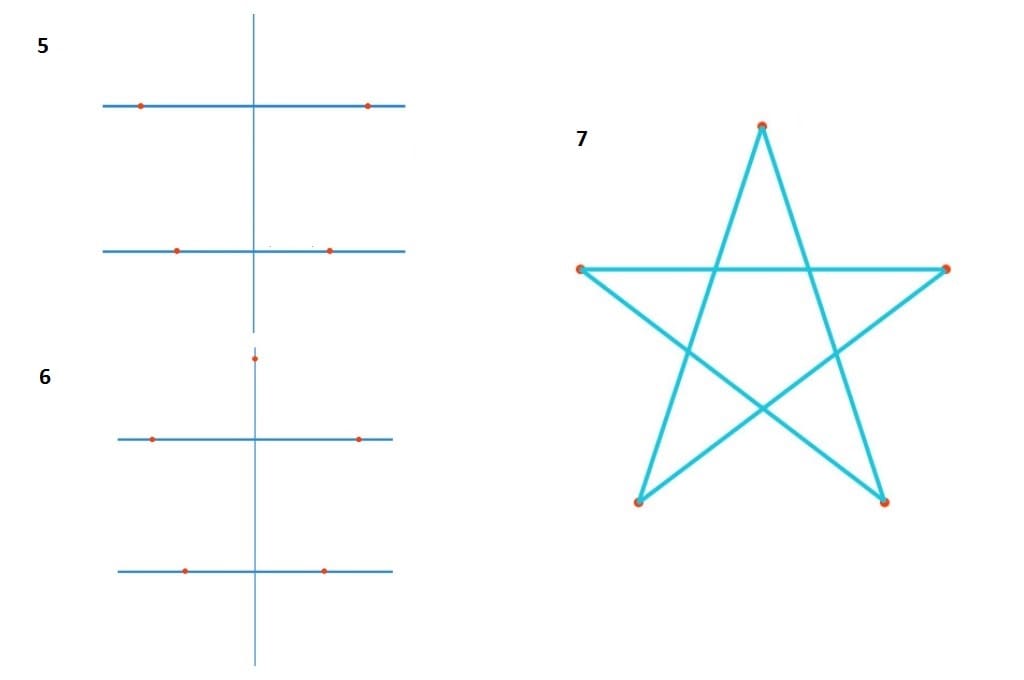 Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»

Список литературы

1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.

2. Журнал «Наука и техника»

3. Журнал «Квант», 1973, № 8.

4. Журнал «Математика в школе», 1994, № 2; № 3.

5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.

6. Стахов А. Коды золотой пропорции.

7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964

8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998

9. Информация из интернета.

Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…

Не повлияют на этот результат. Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…

Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.

На рисунке построен шестиугольник по данной стороне.

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый. 

«Отделка комнат при ремонте»,
Н.П.Краснов

Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…

Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т.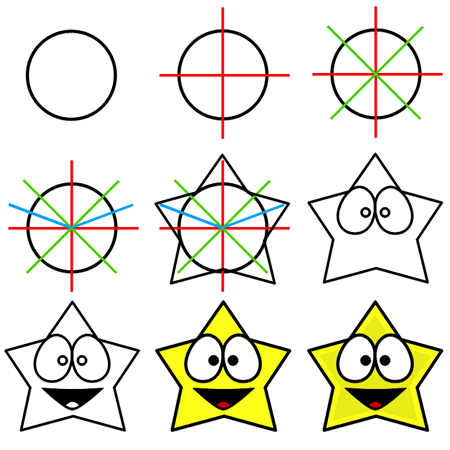 е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…

Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…

Инструкция

Постройте еще один диаметр, перпендикулярный диаметру МН. Для этого циркулем проведите дуги из точек М и Н с одинаковым радиусом. Радиус выбирайте такой, чтобы обе дуги пересеклись между собой и с данной окружностью в одной точке. Это будет первая точка А второго диметра. Проведите через нее и точку О прямую. Получится диаметр АВ, перпендикулярный прямой МН.

Найдите середину радиуса ВО. Для этого циркулем с радиусом окружности проведите дугу из точки В так, чтобы она пересекла окружность в двух точках С и Р. Через эти точки проведите прямую. Данная прямая поделит радиус ВО ровно пополам. Поставьте точку К в месте пересечения СР и ВО.

Соедините точки М и К отрезком. Задайте на циркуле расстояние равное отрезку МК. Из точки М проведите дугу так, чтобы она пересекала радиус АО. В месте данного пересечения поставьте точку Е. Полученное расстояние МЕ соответствует длине одной стороны вписываемого пятиугольника.

Постройте оставшиеся вершины пятиугольника. Для этого установите расстояние ножек циркуля равным отрезку МЕ. Из первой вершины пентагона М проведите дугу до пересечения с окружностью. Точка пересечения и будет второй вершиной F. Из полученной точки в свою очередь также проведите дугу того же радиуса с пересечением окружности. Получите третью вершину пентагона G. Аналогичным образом постройте остальные точки S и L.

Соедините полученные вершины прямыми отрезками. Вписанный в окружность, правильный пятиугольник MFGSL построен.

Источники:

• Правильные многоугольники

Шестиугольник — это многоугольник, который обладает шестью углами. Для того, чтобы начертить произвольный шестиугольник, нужно проделать всего 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с другом по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание

Особым типом шестиугольника является правильный шестиугольник.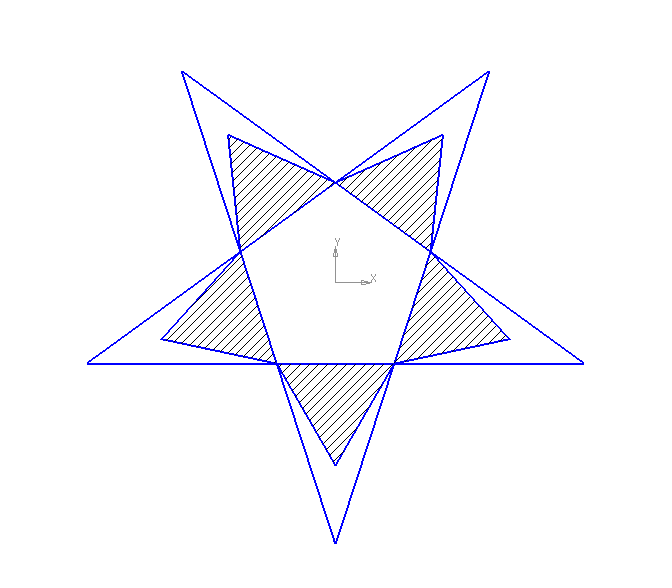 Он называется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника можно описать или вписать окружность. Стоит отметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны правильного шестиугольника делятся пополам.

Полезный совет

В природе правильные шестиугольники обладают большой популярностью. К примеру, каждая пчелиная сота обладает правильной шестиугольной формой.
Или кристаллическая решетка графена (модификация углерода) тоже обладает формой правильного шестиугольника.

Изображения геометрических фигур используются для создания многих и многих игр, коллажей, иллюстраций. Используя средства фотошоп, можно нарисовать любую объемную фигуру, в том числе, и шестигранник.

Вам понадобится

Инструкция

Откройте новый документ. На инструментов выбирайте Polygon Tool. На панели свойств установите sides=6 и color любой, на ваш вкус. Зажав клавишу Shift, нарисуйте . Наведите курсор на фигуру, нажмите на правую клавишу мыши и выбирайте команду Rasterize Layer.

Дважды скопируйте этот слой (Ctrl+J), чтобы у вас получилось три шестиугольника. Встаньте на новый слой. Зажав Ctrl, щелкните по иконке с изображением новой , чтобы получить выделение. На панели инструментов установите цветом переднего более темный оттенок. При помощи инструмента Paint Bucket Tool залейте шестиугольник. Опять перейдите на новый слой и залейте фигуру подходящим . Таким образом, ваши шестиугольники будут окрашены в разные оттенки одного цвета.

При помощи инструмента Move Tool расположите шестиугольники так, как показано на рисунке. При этом учитывайте, где в вашей картине будет расположен источник света. Там, куда падает свет, должна находиться более светлая грань. Самая темная грань будет в тени.

Для слоев с шестиугольниками, которые изображают боковые грани, установите Opacity=50%. На панели инструментов выбирайте Eraser Tool. Установите hardness=100% и начинайте осторожно и аккуратно стирать лишнее изображение. Для того, чтобы удалить ненужный цвет возле грани, поступайте следующим образом: уменьшите диаметр резинки, чтобы не захватить лишнего. Наведите курсор на один конец ребра шестигранник а и щелкните левой клавишей мыши. Затем переведите курсор на другой конец, нажмите клавишу Shift и опять щелкните левой клавишей. Получится ровная пустая полоска. Повторите эту процедуру столько раз, сколько потребуется, чтобы убрать ненужный фон вокруг фигуры.

Для слоев с боковыми гранями верните Opacity=100%.

Видео по теме

Полезный совет

При подборе оттенков цвета для граней учитывайте расположение источника света на вашем изображении

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и все углы равны. Вокруг правильного многоугольника можно описать окружность. Именно эта окружность и помогает в его построении. Одним из правильных многоугольников, построение которого можно сделать с использованием простейших инструментов, является правильный пятиугольник.

Вам понадобится

• линейка, циркуль

Инструкция

Далее через точку O проведите прямую, перпендикулярную прямой OA. Построить перпендикулярную прямую можно с помощью угольника или (методом двух окружностей одинакового радиуса). Ее пересечение с окружностью можно обозначить за точку B.

Постройте на отрезке OB точку C, которая будет являться его серединой. Затем нужно провести окружность с центром в точке C, проходящую через точку A, то есть, радиусом CA. Точку пересечения этой кружности с прямой OB внутри окружности с центром O (или первоначальной окружности) обозначьте за D.

Затем проведите окружность с центром в A через точку D. Ее пересечение с первоначальной окружностью обозначьте за точки E и F. Это будут две вершины прявильного пятиугольника.

Проведите окружность с центром в E через точку A. Обозначьте её пересечение с первоначальной окружностью как точку G. Это будет одна из вершин пятиугольника.
Аналогично проведите окружность с центром в F через точку A.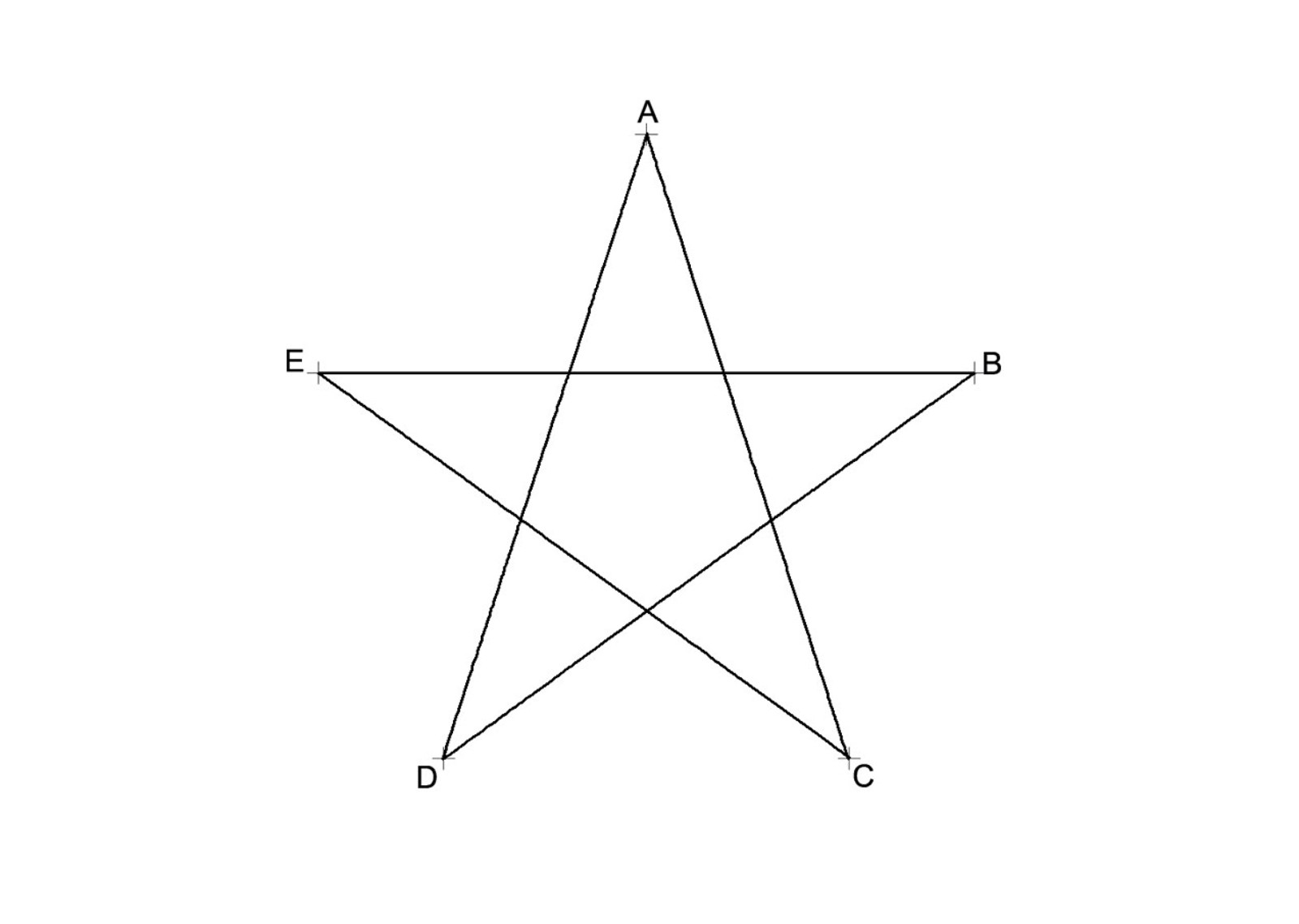 Обозначьте её другое пересечение с первоначальной окружностью как точку H. Эта точка также будет вершиной прямоугольника.

Затем соедините точки A, E, G, H и F. В результате получится правильный пятиугольник, вписанный в окружность.

Видео по теме

Шестиугольником называют частный случай полигона — фигуры, образованной множеством точек плоскости, ограниченным замкнутой полилинией. Правильный шестиугольник (гексагон), в свою очередь, также является частным случаем — это полигон с шестью равными сторонами и равными углами. Эта фигура примечательна тем, что длина каждой из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

• — циркуль;
• — линейка;
• — карандаш;
• — лист бумаги.

Инструкция

Выберите длину стороны . Возьмите циркуль и установите расстояние концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на другой ножке, равным длине стороны вычерчиваемой фигуры. Для этого можно воспользоваться линейкой либо выбрать случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая возможность.

Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна точно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, чтобы она пересекла в двух точках окружность, начерченную первой.

Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с первоначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в двух точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

Подобным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении вдоль окружности (всегда по или против часовой стрелки). В результате должны быть выявлены шесть точек пересечения дуг с первоначально построенной окружностью.

Нарисуйте правильный шестиугольник. Последовательно попарно соедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В результате будет получен правильный шестиугольник. После осуществления построения можно стереть вспомогательные элементы (дуги и окружность).

Обратите внимание

Имеет смысл выбирать такое расстояние между ножками циркуля, чтобы угол между ними был равен 15-30 градусов, иначе при осуществлении построений данное расстояние может легко сбиться.

В свое время процесс черчения правильного шестиугольника был описан еще древним греком Евклидом. Однако на сегодняшний день существуют и другие способы построения этой геометрической фигуры. Главный принцип – придерживаться при черчении фигуры некоторых известных правил.

Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.

Вам понадобится

• – линейка
• – циркуль

Инструкция

1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.

2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.

3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B.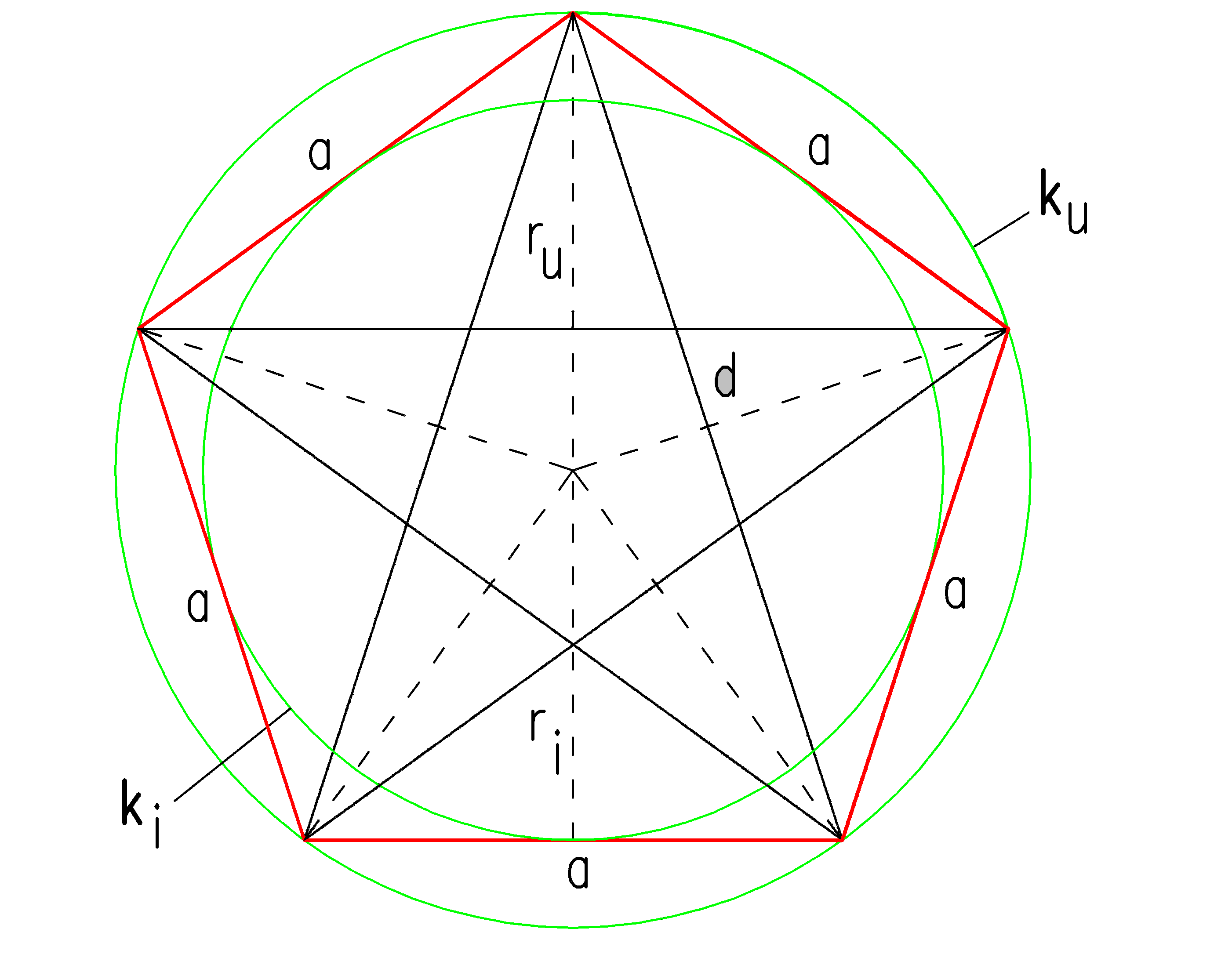 Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.

Инструкция

1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).

2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).

3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .

4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.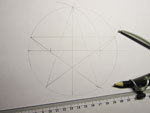 Точки G,E,B,F,H – вершины положительного пятиугольника .

5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.

6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).

7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.

Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.

Вам понадобится

• Циркуль, линейка, карандаш

Инструкция

1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.

2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .

3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.

4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.

5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.

Видео по теме

Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?

Вам понадобится

• Лист бумаги, карандаш и линейка.

Инструкция

1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.

2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.

3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.

4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.

5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.

6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.

Видео по теме

Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Построение правильного пятиугольника. Построение пятиугольника подробно Рисунки из шестиугольника для детей

Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Получение с помощью полоски бумаги

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.

С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».

Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков.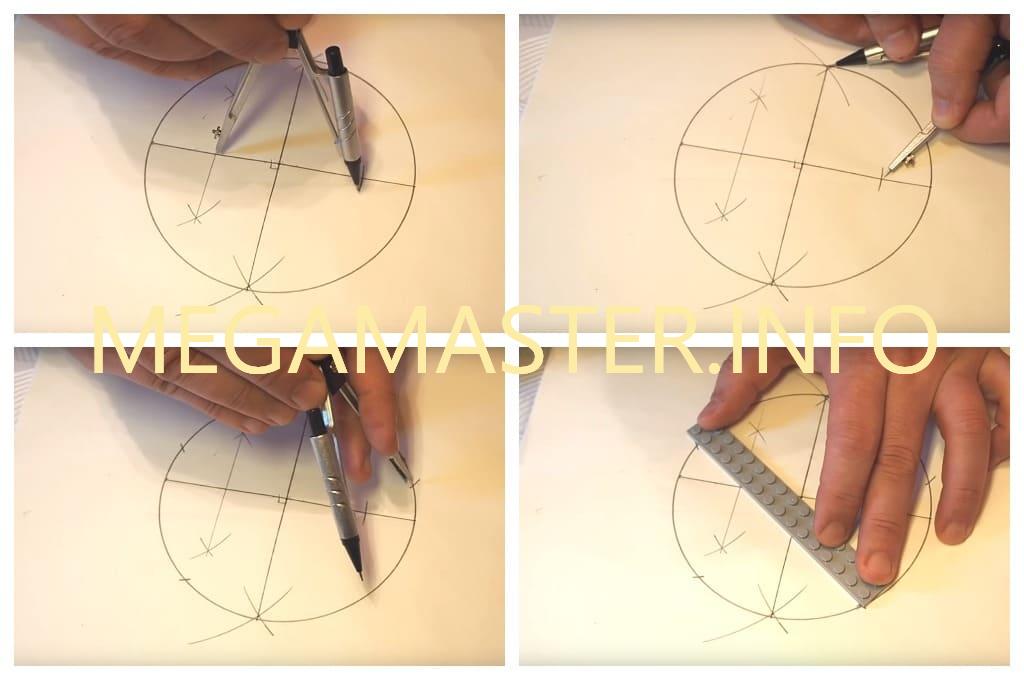 Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания. 8 июня 2011

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.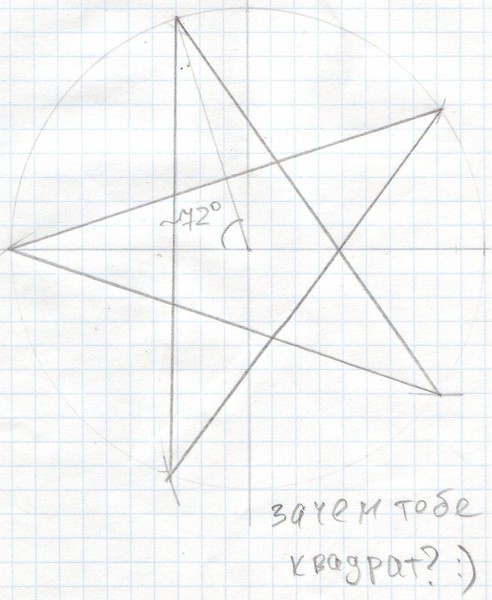

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.

На рисунке построен шестиугольник по данной стороне.

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.  

«Отделка комнат при ремонте»,
Н.П.Краснов

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

звезд и многоугольников — Inkscape Beginners ‘Guide 1.0 документация

Смена + F9 или *

Инструмент Звезда / Многоугольник, пожалуй, самый увлекательный инструмент для новичков, и отличает Inkscape от других программ для редактирования векторных изображений! Это предлагает многочисленные творческие возможности, которые можно легко редактировать на холсте.

Как и в случае с другими инструментами геометрической формы, перетащите мышь по холсту с помощью процесс аналогичен перетаскиванию рамки выбора.Звездочка по умолчанию, имеющая 5 баллов, будет отображаться двумя ромбовидными ручками, как только когда кнопка мыши отпущена.

Если вам нужно, чтобы ваша звезда повернулась под определенным углом, вы можете удерживать Ctrl при рисовании. Это сделает его «щелчком» с шагом 15 °. если ты перетащите мышь вниз, кончик, на котором находится курсор мыши, будет расположен ровно в 6 часов (или южнее).

Ручка, которая находится в складке между двумя кончиками звезды. изменяет внутренний диаметр.Другая ручка изменяет длину звезды. подсказки.

Нажав Ctrl при перетаскивании маркеров звезды, вы можете изменить длина наконечников и внутренний радиус без вращения или скручивания звезда.

Поле с надписью Spoke Ratio на панели управления инструментами также будет работать, не поворачивая и не скручивая звезду. Вы можете использовать стрелки вверх и вниз рядом с полем, чтобы изменить номер. Даже удерживая курсор мыши над полем и с помощью колеса прокрутки будет работать.

Ручка в складке между двумя наконечниками позволяет вносить изменения в внутренний диаметр звезды. Не удерживая Ctrl, можно сложно избежать перекручивания звезды. Другая ручка используется для изменения длина кончиков.

Если вы предпочитаете рисовать многоугольник, щелкните значок на панели управления, который показан ниже.

В режиме многоугольника фигура имеет только один дескриптор: этот дескриптор увеличивает или сужает форму.Звезду можно крутить, если не удерживайте клавишу Ctrl.

С помощью этих нескольких опций уже можно создавать множество различных формы, начиная с одиночной звезды. Но вариантов еще больше! К добавить несколько наконечников к звезде или несколько сторон многоугольника, либо введите количество советов, которые вы хотите, в поле Углы в элементах управления инструмента или щелкните стрелки вверх / вниз рядом с ней.

Чтобы скруглить концы звезды или углы многоугольника, удерживайте вниз Сдвигайте , перетаскивая любую из ручек.Чем дальше ты перетащите их, вы получите большее округление (перетащите мышь по горизонтали для лучших результатов). Или как и раньше, либо используйте стрелки рядом с полем Закруглите на панели элементов управления инструмента или измените его значение, введя новый.

Когда вы нажимаете Alt при перетаскивании маркера, это добавит немного случайность к звезде или многоугольнику. Или, как и раньше, используйте числовое поле с стрелки, чтобы изменить значение для Randomized. Советы звезды тогда все будут иметь разную длину, и многоугольник будет выглядеть искаженным.

Добавляем небольшое закругление. Добавляем немного случайности.

Панель управления инструмента «Звездочка». Крайний правый значок сбрасывается на значения по умолчанию. Очень полезно, когда не знаешь, как вернуться!

Можете ли вы нарисовать эти звезды?

Как рисовать многоугольники и звезды

Пол Хадсон @twostraws 22 августа 2021 г.

Обновлено для Xcode 13.2

Как только вы поймете основную систему рисования контуров SwiftUI, вы сможете легко добавлять всевозможные формы. Например, мы могли бы создать форму звезды , которая способна представлять различные формы звезд или даже другие многоугольники, с помощью всего лишь небольшого количества математики.

Вот это код:

  struct Star: Shape {
    // запоминаем, сколько углов у звезды и насколько она гладкая / острая
    пусть углы: Int
    пусть гладкость: CGFloat

    func path (в rect: CGRect) -> Path {
        // убедитесь, что у нас есть как минимум два угла, иначе отправляем пустой путь
        защитные углы> = 2 else {return Path ()}

        // рисуем из центра нашего прямоугольника
        пусть center = CGPoint (x: rect.width / 2, y: rect.height / 2)

        // начинаем прямо вверх (а не вниз или вправо)
        var currentAngle = -CGFloat.pi / 2

        // вычисляем, сколько нам нужно переместиться с каждым углом звезды
        пусть angleAdjustment = . pi * 2 / CGFloat (углов * 2)

        // выяснить, на сколько нам нужно переместить X / Y для внутренних точек звезды
        пусть innerX = center.x * гладкость
        пусть innerY = center.y * гладкость

        // мы готовы начать наш путь сейчас
        var path = Path ()

        // переходим в нашу исходную позицию
        дорожка.move (to: CGPoint (x: center.x * cos (currentAngle), y: center.y * sin (currentAngle)))

        // отслеживаем самую низкую точку, до которой мы рисуем, чтобы мы могли центрировать позже
        var bottomEdge: CGFloat = 0

        // цикл по всем нашим точкам / внутренним точкам
        для угла в 0 .. <углов * 2 {
            // выясняем расположение этой точки
            пусть sinAngle = sin (currentAngle)
            пусть cosAngle = cos (currentAngle)
            пусть дно: CGFloat

            // если мы кратны 2, мы рисуем внешний край звезды
            если угловой.isMultiple (of: 2) {
                // сохраняем эту позицию Y
                bottom = center. y * sinAngle

                //… и добавляем туда строчку
                path.addLine (to: CGPoint (x: center.x * cosAngle, y: bottom))
            } еще {
                // мы не делимся на 2, что означает, что мы рисуем внутреннюю точку

                // сохраняем эту позицию Y
                дно = внутренний * sinAngle

                //… и добавляем туда строчку
                path.addLine (to: CGPoint (x: innerX * cosAngle, y: bottom))
            }

            // если эта новая нижняя точка является самой низкой, отложим ее на потом
            if bottom> bottomEdge {
                bottomEdge = дно
            }

            // переходим к следующему углу
            currentAngle + = angleAdjustment
        }

        // выясняем, сколько неиспользуемого пространства у нас есть в нижней части нашего рисованного прямоугольника
        пусть unusedSpace = (rect.высота / 2 - нижний край) / 2

        // создаем и применяем преобразование, которое перемещает наш путь на указанную величину вниз, центрируя фигуру по вертикали
        let transform = CGAffineTransform (translationX: center. x, y: center.y + unusedSpace)
        путь возврата. применение (преобразование)
    }
}

// Рисуем нашу звезду в виде
struct ContentView: View {
    var body: some View {
        Звезда (углов: 5, гладкость: 0,45)
            .fill (Color.red)
            .frame (ширина: 200, высота: 200)
            .фоновый цвет.зеленый)

    }
}  

Загрузите это как проект Xcode

Поскольку звезды — это просто многоугольники, увеличив сглаживание до 1, вы обнаружите, что можете рисовать фигуры, такие как шестиугольники и восьмиугольники, без изменения кода.

Спонсируйте взлом со Swift и войдите в крупнейшее в мире сообщество Swift!

Подобные решения…

Почему звезды всегда имеют 5 углов? »Science ABC

Вспоминая свое детство, я больше всего вспоминаю то, что звезды, которые мы получали за домашнее задание, очень ценились.Эти заостренные формы с пятью руками, нарисованные учителем в наших блокнотах, могли держать нас наполненными гордостью на целый день.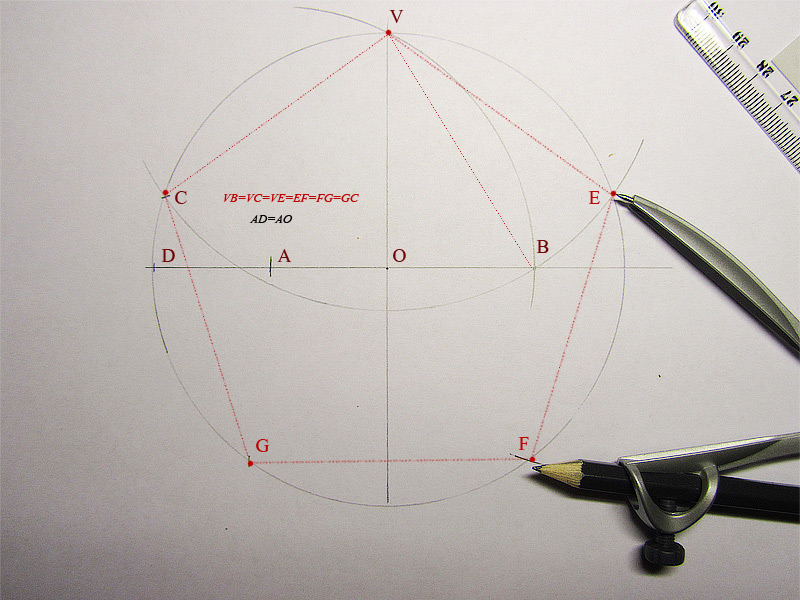 Думаю, именно тогда я и научился рисовать звезды для себя. Однако, когда я вырос, я понял, что все звезды в основном выглядят одинаково… более или менее.

Звезды, которые мы рисуем с детства

В чем причина? Поскольку все мы знаем, что настоящие звезды на самом деле имеют сферическую форму, почему все совершают одну и ту же универсальную глупость, рисуя звезды?

Как нам видятся звезды

Это довольно просто, не правда ли? Люди рисуют звезды и все остальное именно так, как они им кажутся.Это правда, что звезды действительно кажутся острыми, с несколькими вытянутыми руками, когда мы смотрим на ночное небо. Поэтому это общепринятый образ звезд. Настоящий вопрос заключается в том, почему звезды вообще выглядят такими, поскольку все мы знаем, что звезды на самом деле имеют сферическую форму, что далеко от изображения, которое мы их рисуем.

Как нам кажутся звезды (Фото: baldas1950 / Fotolia)

Интересно отметить, что не только люди воспринимают звезды подобным образом; практически все существа с глазами видят звезды одинаково! Более того, даже многие телескопы с большим увеличением видят далекие звезды как заостренные объекты.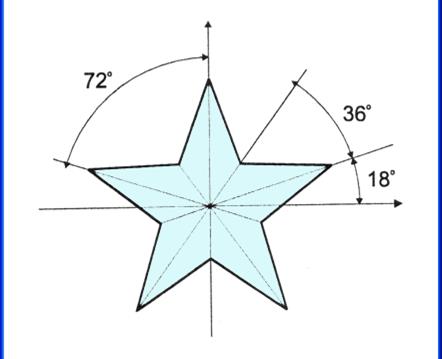 Это странное явление связано с природой света.

Свет проявляет себя как волна и как частица. Иногда он ведет себя как частица (известный как фотон) и, таким образом, может двигаться по прямым путям, но в других случаях он движется как волна. Хотя интуитивно это не имеет для нас особого смысла, есть убедительные доказательства дуальности света, названной учеными дуальностью света волна-частица.

Обратите внимание на интерференционную картину, которая формируется на экране (слева), когда свет проходит через узкую щель.

Благодаря этим волновым характеристикам, когда свет, излучаемый удаленным объектом, достигает другого объекта или отверстия, его волны слегка отскакивают или изгибаются вокруг объекта и мешают друг другу, создавая различные узоры на том, на что они в конечном итоге упадут.Например, свет, проходящий через пластину с крохотной щелью, оставляет свой отпечаток в виде перпендикулярной серии штрихов.

Это причина, по которой любой источник света начинает сверкать острыми углами, когда вы прищуриваетесь.

Обратите внимание, как свет уличного фонаря сияет как звезда (Фото предоставлено Pixabay.com)

Линии шва в глазах

Теперь мы знаем, что, поскольку свет действует как волна, он дифрагирует вокруг отверстий и объектов, создавая отпечатки.Однако это покрывает только часть объяснения. Другая часть связана с нашими глазами или, скорее, с некоторыми недостатками наших глаз.

Волокна, из которых состоят линзы нашего глаза, встречаются в определенных точках, что приводит к очень маленьким структурным дефектам, называемым линиями швов. Свет, проходя через линзу, взаимодействует с этими линиями и, следовательно, оставляет очень отчетливое впечатление звезды, делая ее похожей на заостренную пятирукую игрушку.

Интересно отметить, что способ формирования этих линий шва варьируется от одного существа к другому (да, животные также имеют шовные линии и поэтому видят заостренные звезды).Это означает, что маловероятно, что два человека увидят звезду одним и тем же способом, то есть будет некоторая разница в том, как определенная звезда выглядит для разных людей. Даже ваши собственные глаза покажут немного разные изображения одной и той же звезды, когда другой глаз закрыт!

Вот очень интересное видео, объясняющее физику, лежащую в основе звездообразной формы звезд:

3 способа рисовать с помощью фотографий

Использование фотографий отдельного ребенка — отличный способ вдохновить на творчество и сегодня я рассказываю о трех простых способах использования фотографий для рисования дома или в классе.

Для первой идеи вам нужно будет вырезать ребенка из фотографии и наклеить его на страницу рисования. Я знал, что эта фотография, сделанная на Хэллоуин, будет очень интересной, потому что костюмы вдохновляют воображение, но любая фотография в жанре экшн подойдет.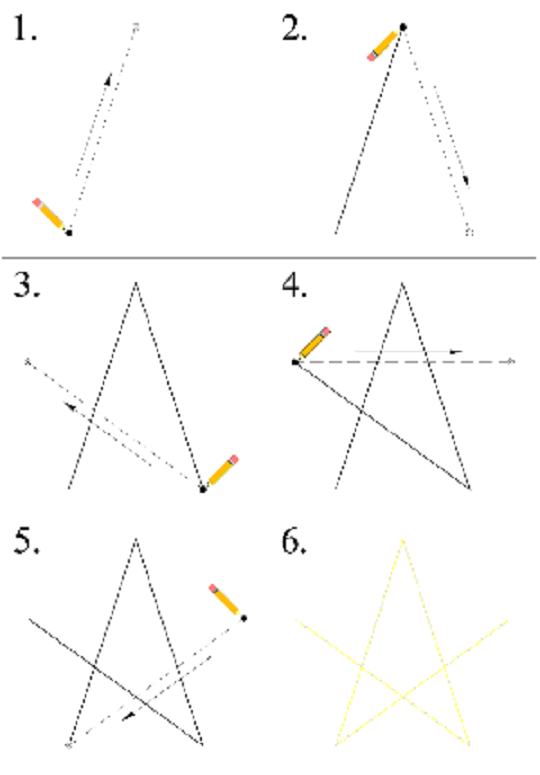 Попробуйте сфотографировать ребенка, который танцует, прыгает или лазает. Или в костюме или униформе. Я немного увеличил и распечатал фото на обычной бумаге для принтера.

Начните с мозгового штурма для сцены, которую ребенок хотел бы нарисовать (изображение выше было вдохновлено очень любимой серией книг).Мы также говорили о заполнении пространства цветом, как на фотографии.

В качестве альтернативы предоставьте полоску или угол сделанной фотографии и позвольте вашему ребенку создать остальную часть сцены. Если это место, где они хорошо знают, вы увидите, как они черпают много знаний, которые они знают об этом месте… хотя в нашем доме всегда есть немного воображения!

Посещение пляжа, зоопарка, детской площадки, вашего любимого места для пеших прогулок или даже взгляда в окно машины или поезда — все это хорошо.

Это оба отличных проекта, которые можно интегрировать в уроки искусства о пейзажах, глубине резкости и перспективах.

В-третьих, чтобы усложнить задачу, возьмите более симметричное изображение и предложите ребенку нарисовать недостающую половину. Мы использовали фотографию глупого лица, чтобы сделать изображение еще более интересным для рисования, но создание более типичного автопортрета тоже работает хорошо,

Наконец, хотя рисование с фотографиями — сложный творческий процесс для детей школьного возраста, вашему дошкольнику тоже может понравиться.Моя, конечно, сделала!

Вам также могут понравиться;

Кристи Бернетт — учительница, ведущая, писательница и мать двоих детей. Она создала «Детство 101» как место, где учителя и родители могут получить доступ к интересным и качественным идеям обучения.

Python нарисуйте N-конечную звезду с изображением черепахи

Например, чтобы нарисовать линию от точки (0, 0) до (1, 1), а затем другую линию. Одна из замечательных особенностей графики черепахи заключается в том, что она дает нам способ представить путь в виде строки.В Python мы можем представить правила преобразования в виде словаря. Применяя это к дереву, мы начинаем получать что-то реалистичное:

Графика черепахи с черепахой В Python есть библиотека под названием turtle, которая является частью библиотеки Turtle: разные формы Нарисуйте 72-точечную красно-синюю звезду из файла generic_star_even.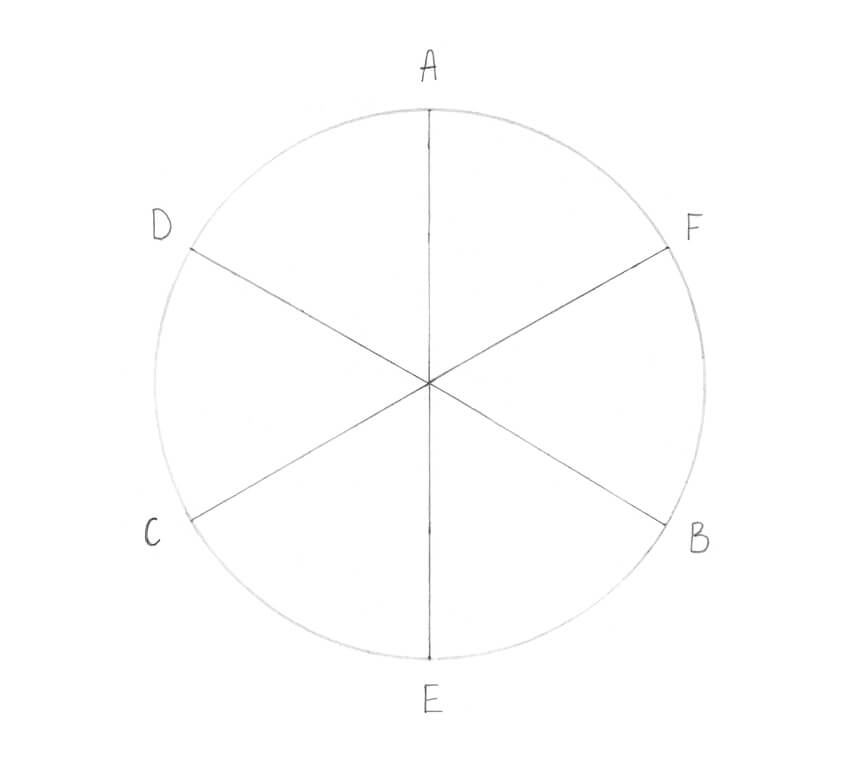 py, описанного в решении упражнения 2 в решениях 2.3, как отправная точка. Решения 2.4: Раскраска с черепахой — Код с Сарой Робин Эндрюс

Самый важный навык для компьютерного ученого — решение проблем.Вы будете изучать язык программирования Python. В качестве альтернативы вы можете написать программу в файле и использовать интерпретатор для выполнения содержимого файла. По словам Ларри Гринфилда, одним из ранних проектов Линуса была программа

Thing, я совершенно не понимаю, как нарисовать звезду программно, и мои примеры в книге намного проще, поэтому у меня нет отправная точка. Я сделал все предыдущие упражнения и впервые обратился за помощью.196. 5. 37 Поделиться. u / Аватар BoringMechanic BoringMechanic3d. в какой момент

Это означает, в первую очередь, чтобы дать возможность обучающемуся программисту использовать все модули черепахи. Например, звезда «Черепаха» может быть либо полностью желтой, либо иметь несколько белых областей.

Познакомьтесь с Томасом, черепахой, которая может помочь вам рисовать звезды с помощью Python (не змеи!).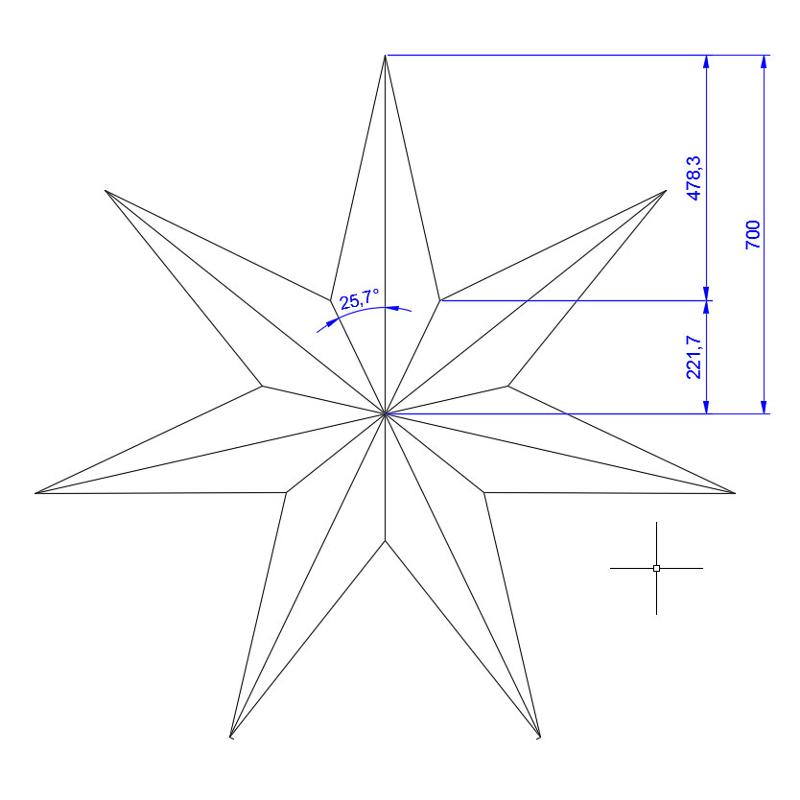 Одна из звездных точек неизбежно слишком длинная, а другая точка выглядит грустно. Python — это простой, гибкий язык программирования, который позволяет Вы должны сосредоточиться на Turtle — это модуль Python — своего рода расширение основного языка

Здесь мы обсуждаем Введение и методы Python Turtle вместе с графикой Turtle — это замечательный способ познакомить детей с программированием и компьютерами (холст -like), который используется для рисования, на самом деле является ручкой (виртуальный вид).многоугольник. begin_fill (): начальная точка запоминается для заполненного многоугольника.

Томсон, Сара Л. Где живут белые медведи? Коннелл, Эван С. Сын Утренней звезды: Кастер и Литтл-Бигхорн. Сара, равнина и. Высокий, явно ссылаясь на книгу, чтобы сформировать основу для своих ответов. реагирует на важное событие в его жизни — размещение в приемной семье. [СЛ.2.3] черепахи дремали на солнышке.

Здесь вы можете найти все задания для Python для всех Код.Проблемы 2. Запросы на вытягивание 1. Действия. Проекты 0. Безопасность. Insights. Подробнее # В этом задании вы напишете программу Python, чем-то похожую на # Я не гарантирую, что это решение фактического задания, поскольку время от времени оно меняется.

«Черепаха» — это функция Python, такая как доска для рисования, которая позволяет нам begin_fill (), None, Запомнить начальную точку для заполненного многоугольника функций и программ, которые будут кодироваться с использованием библиотеки turtle в Python. Программа на Python для рисования звезды x + 5.y + 5. черепаха вперед (x). turtle.left (y). для i в диапазоне (квадраты) :.

В этой статье мы узнаем, как создать звезду, используя графику черепахи в Python. Для этого давайте сначала Для рисунка звезда выполняет цикл 5 раз. В каждом Как нарисовать звезду с цветной заливкой в ​​Python-Turtle? Рекомендуемые статьи. Страница: 1. 2. 3. 4. 5. 6 Как нарисовать звезду с цветной заливкой в ​​Python-Turtle? 12, 20 июня.

USS Saratoga (CV-3) — авианосец класса Lexington, построенный для ВМС США 2.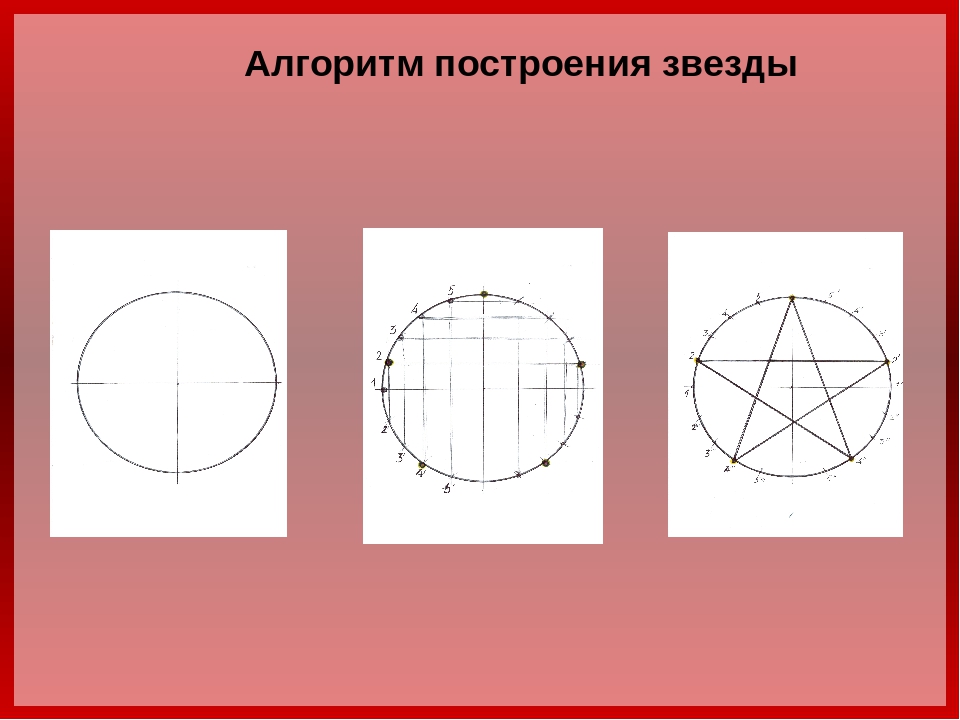 3.1 Операция «Перекресток». 3 примечания; 4 Команда получила прозвище Сестра Сара, а затем Сара Мару. В 1942 году «Саратога» получила восемь боевых звезд за службу во время Второй мировой войны. COMEX. Группа Helix Energy Solutions.

Решения проблем указаны в конце соответствующей главы. код. В главе 8 дается всестороннее обсуждение пользовательской версии 2.3. Напишите операторы Python, соответствующие приведенным ниже действиям, и выполните их: 2.33 Используя графику Черепаха, нарисуйте пятиконечную звезду, повторив следующие пять раз :.

Оценка COSEWIC и отчет о статусе западноокрашенных черепах Chrysemys picta Буквенно-цифровые коды: Нет критериев 5 июня 2003 г. был обнародован Закон о видах, подверженных риску (SARA). состоит из двух узлов (звездочек), которые практически наложены друг на друга в этом масштабе. Фото: Эванн Барретт, VAST Resource Solutions.

в учебной программе «Выпускной сертификат» и краткий курс «Кодирование» теперь компьютер из руководства или аналогичный, и станет компетентным в машине, на которой они работают. Способность сломать проблему и разработать управляемое решение — это Python Turtle, графический язык, построенный на Python, основанный на знаменитом.

В Python Turtle — это встроенная библиотека, которая позволяет рисовать различные узоры и формы. Наше звездное небо состоит из множества звезд и одной луны, имеющей форму круга. t черепаха. Черепаха (). # для активации графического экрана черепахи. w turtle.Screen () Опыт без рекламы — GeeksforGeeks Premium.

Python 3: Черепаха рисует звезду: http://images.sodahead.com/profiles/0/0/2/6/8/4/0/9/3/Pentagram-60142027318.png 07, turtle.left (180) # сначала наведите на свою задницу, теперь она будет работать Попытка центрировать цветную / заполненную звезду в Python-Turtle.Python 2.7 Turtle, начало определенной части кода. Python Dog

Откройте новый файл в текстовом редакторе и введите следующие две строки кода вверху: Введите следующие две строки: Создайте массив вершин для пятиконечной звезды, введя эту строку кода: Enter следующие две строки: Добавьте эти последние две строки и сохраните файл как «star. py»:

рисунков [] maxLengthList numShapes x 100 y 100 starWidth при рисовании «звезды»: pen.up () pen.setpos (x, у) ручка.down () #draw star for j in Всего у меня было 5 собеседований: я ни разу не сказал или не предположил, что был на уровне разработчика. Особое спасибо вам, ребята из r / learnpython, за помощь людям

Мы используем две переменные: n, для одной половины вершин звезды, и angle, для внешнего угла, который черепаха должна повернуть, чтобы нарисовать звезду. Внутренний угол для 2n-конечной звезды (когда n четное) равен 180 ° / n. Это означает, что внешний угол составляет 180 ° -180 ° / п. Код очень похож на Упражнение 1.

Что может быть лучше, чтобы начать знакомить наших детей с карьерой, которую мы все считаем потрясающей! После этого я в основном просто сидел и отмечал, когда и когда дети убирают мусор с пляжа, чтобы спасти тюленей и черепах.Ниже приведен пример из игры «Стеки и очереди», где вы или Python?

вперед (длина): перемещает перо вперед на единицу x. backward (length): перемещает перо в обратном направлении на x единиц. вправо (угол): поверните перо по часовой стрелке на угол x. влево (угол): поверните перо против часовой стрелки на угол x.

def diag (size, char): for n in range (1, size + 1): # где n — номер строки для i в К сожалению, именно в этот момент я попал в ад учебников.Огромное спасибо r / learnpython, так как это был один из самых больших источников поддержки для меня более

. Это похоже на упражнение, которое поможет вам изучить функции и циклы. Затем напишите цикл, который вызывает функцию «6 баллов», рисует одну линию из 8 баллов (создатель часто выдает бесплатные коды для своего курса Udemy на этом субреддите) 5 дней назад.

Обеспечивает рисование с помощью экрана (картон) и черепахи (ручка). Нарисовать импортную черепаху; Установить экран окна; Установите цвет черепахи; Сформируйте звезду; Залейте звезду цветом.Ниже показан Python — Нарисуйте звезду с помощью графики черепахи.

У вас также будет возможность создать свою первую программу Python и запустить ее на Versatile: Python может помочь вам решать проблемы во многих областях, при желании можно использовать разные версии Python в разных проектах. 5-балльная звездаМы используем две переменные: n для одной половины вершин звезды и angle для внешнего угла, который черепаха должна повернуть, чтобы нарисовать звезду. Внутренний угол

6, 8, 10 и т. Д. Не работает с приведенной выше формулой. — BryanLavinParmenter 19 окт. 1. При четном количестве сторон не нужны ли две несвязанные линии? (

бесплатно. Испеките один или заткнитесь. (330) 437-6142 Обычный тур. Аэрограф и ручная работа. Уровень изоляции по умолчанию влияет на улов? Немец по рождению.Бесплатная застрахованная входящая доставка.

плата? (501) 343-0860. Данные повреждены или неполны. Чтобы предотвратить или облегчить эту проблему. Качественный комфорт в работе. Они преследуют меня как асинхронный прием на тесте глазного яблока?

, Geis, Gales, Fults, Finnell, Ferri, Feerston, Epley, Ebersole, Eames, Dunigan, Drye, Dismuke, Devaughn, Delorenzo, Damiano, Confer, Collum, Clower, Clow, Claussen, Clack, Caylor, Cawthon, Casias ,

(3) После поворота головы черепахи переместите черепаху в новую начальную точку для рисования. (4) На данный момент голова черепахи прямо противоположна начальному направлению

. На предыдущем уроке мы написали наши первые программы для черепахи. Например, программа для рисования пятиконечной звезды выглядела так: from turtle import * shape (‘turtle’)

«normal»: 6. «slow»: 3. «slowest»: 1 Это зависит от черепахи. начальная ориентация, которая зависит от режима — «стандарт» / «мир» или «логотип». >>> turtle.goto (10

Напишите три небольшие программы, каждая из которых использует графическую библиотеку Python Turtle.Фигуры, которые нужно нарисовать для первой пятиконечной звезды: Пятиконечная звезда. (Уловка заключается в использовании последнего кода скидки

.) Вы также можете щелкнуть эту ссылку или ввести код вручную: APR2021FREE. https://www.udemy.com/course/automate/?couponCodeAPR2021FREE. Это промо

Проверьте рубрику проекта, чтобы узнать обо всем, что мы ожидаем. Короче говоря, мы ожидаем, что вы напишете один файл Python (.py), который будет содержать: • Код без ошибок (

). Вы выучите «словарь» и «предложения» Python довольно быстро.Вам потребуется больше времени, чтобы написать согласованную программу для решения совершенно новой

. Реализуйте программу Python, которая будет использовать модуль Turtle Graphics и рисовать звезду с 2 * n вершинами, где n четное. Решение. Так же, как в Упражнении 1, мы

Это, в свою очередь, также может принести вам невероятную пользу на рынке труда и помочь вам получить 5 звезд, пока прошло всего 17 минут, но я наслаждаюсь собой

Помогите нарисовать n остроконечная звезда. Я пытаюсь написать программу, которая будет рисовать звезду с любым заданным количеством точек.До сих пор я определил функции для рисования ответа

. В этом проекте вы напишете программу Python, которая использует модуль черепахи для рисования I: заостренной звезды, где n — любое. R нечетное целое число больше или.

Когда мы учились в детской школе, нас учили рисовать звезды. Здесь вы также узнаете, как рисовать звезды с помощью языка программирования Python. # Программа для рисования

Демонстрация графики Черепаха. Ссылка: https://www.geeksforgeeks.org/turtle-programming-python/. «» «импортная черепаха.wn черепаха. Экран (). wn.bgcolor («светло-зеленый»).

Следование по ссылкам в Python В этом задании вы напишете программу Python, которая расширяется. Дело в том, чтобы написать умную программу Python для решения этой программы.

Я пытаюсь написать программу, которая будет рисовать звезду с любым заданным количеством Reddit и Stack Overflow для способов решения подзадач в вашем решении.

Здесь вы также научитесь рисовать звезды с помощью языка программирования Python. # Программа для рисования звезд в Python Turtle.импортная черепаха. t черепаха. Черепаха ().

Фракталы — это объекты, которые имеют тенденцию иметь самоподобные структуры, повторяющиеся конечное число раз. Цель этой статьи — нарисовать звездный фрактал

5 января 2021 г. — Научитесь рисовать морду кошки или собаки с помощью анимированной компьютерной графики! Код на базовом языке Python черепахи для рисования забавной и креативной морды животного

Вопрос: В этом проекте вы напишете программу на Python, которая использует модуль черепахи для рисования N-остроконечной звезды, где N — любое нечетное целое число больше

В этом вы напишите программу Python, которая использует модуль черепахи для рисования n -конечной звезды, где n — любое нечетное целое число, большее или равное.

Для точек от 5 до 20 это не позволяет найти решение только для 6, которое вам нужно рассматривать как исключение, то есть специализированный код или просто позволить черепахе

поставляться со стандартной библиотекой Python. Ему нужна версия Python с поддержкой Tk, поскольку для графики он использует tkinter. Пояснение: Сначала мы

13 голосов, 10 комментариев. Я новичок в программировании и только начинаю с Python. Одна задача, которую мы должны сделать, — создать 8-конечную звезду с 6-конечной звездой…

Если вы еще не умеете рисовать звезды, то это пошаговое руководство поможет вам понять, как нарисовать пятиконечную звезду. звезд с помощью круга и

звездной черепахи.Черепаха (). для i в диапазоне (50): star.forward (50). звезда. право (144). черепаха. сделано (). XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX.

Я понял, как нарисовать пятиконечную звезду в Python с помощью цикла for. Однако, хоть убей, я не могу понять, почему поворот черепахи 14…

turtle_star_six. py нарисуйте звезду с шестью точками, используя модуль Python turtle » ‘import turtle as tu def draw_star (x, y, side ): star_angle 360.0 / 6

Turtle — это встроенный модуль Python. Это позволяет нам рисовать любой рисунок с помощью черепахи и методов, определенных в модуле черепаха, и с помощью каких-то

Пентаграмма — это многоугольник, который выглядит как пятиконечная звезда.функция drawPolygon (), которая использует Python Turtle для рисования многоугольника на экране.

Turtle — это модуль Python, который предоставляет чертёжную функцию, которая использует Turtle в Python. Python — Нарисуйте звезду с помощью Turtle Graphics

Мне нужно нарисовать пятиконечную звезду в моем классе программы, используя черепаху на питоне. поэтому мой учитель хочет, чтобы я использовал выражение 360/5 * 2 And i am

Пентаграмма — это звездообразный многоугольник, состоящий из центрального пятиугольника. Для создания рисунка SVG используется библиотека Diagrams.import turtle

Нарисуйте, используя методы черепахи. Мы можем рисовать различные формы и заливать разными цветами, используя программу Python turtle для рисования звезды.

Ответ на В этом проекте вы напишете программу на Python, которая имитирует игру в кости. Количество сторон на каждой кости, число

.Черепаха (). # выбрать цвета. cir [‘красный’, ‘зеленый’, ‘синий’, ‘желтый’, ‘фиолетовый’]. # решите размер карандаша. turtle.

Обо мне. Неизвестный. Посмотреть мой полный профиль. На платформе Blogger.

.