Как нарисовать тетраэдр: Как нарисовать тетраэдр в GIMP? — Хабр Q&A

Содержание

как рисовать тетраэдр — 3 рекомендаций на Babyblog.ru

Опять сто лет не писала… февраль почти весь выпал из жизни в связи с моей болезнью ( Макар, хвала богам (ну и мне, немного), выстоял, не заразился!

А хотела вот о чем — о рисовании! Ну прям ооочень любит он это дело, и с каждым днем все больше и больше ) и если бы мама у Макара не была такой криворукой , а хоть немного умела бы рисовать, то мне кажется Макар уже ого-го как рисовал бы ))

Итак, помимо обычных каляк-мяляк, мы перешли к осмысленному рисованию всякой всячины, в основном рыб ))) этими рыбами он всех ~~достал~~ затерроризировал — почти весь февраль он , а значит и все кто попал в его поле зрения и не успел прикинуться ветошью (и конечно же , в основном , это я ))) ) активно рисуют рыб. Макар торжественно рисует «круг» , который зачастую похож на треугольник, квадрат и тетраэдр одновременно , провозглашает, что это рыба-кит (или какая другая рыба) и требует рисовать ей глаза и зубы. Все остальные части рыбьего тела его интересуют в данном процессе мало, по моей наводке может пририсовать хвост и фонтан (если это все же рыба-кит), но про глаза и зубы не забудет никогда )) все мои рассказы про то, что у китов нет зубов были подвергнуты презрению, а киты стали рисоваться с ОГРОМНЫМИ ЗУБАМИ )) осатанев от китов и прочей рыбьей фауны , я научила его рисовать божьих коровок , и это дело тоже пошло на ура ! жуки , аллилуйя, избегли участи рыб и зубов, а вот лапки им рисовались старательно, много и везде ))

Ну а дальше понеслось — все что он видит или вспоминает требует зарисовки. И я уже не знаю куда деваться от требований нарисовать хурму, пингвина, дракона и прочая и прочая. С учетом того, что виртуозно я могу нарисовать только солнышко ))

Кстати о солнышке , именно с него Макар начал учиться рисовать линии в заданном направлении … и надо сказать неплохо преуспел в этом… потом, подглядев в Умных Книжках рисование по пунктиру, попробовали и его , и тоже неплохо. От прорисовывания пунктирного дождика уже перешли на домики …

С разукрашиванием правда не особо — этот процесс он воспринимает пока что исключительно как игру в прятки, и поэтому то, что нужно разукрасить Макар просто пожирнее и побольше замазывает краской . ни о каком соблюдении границ конечно же тут речи не идет ))

И самый трабл — это то, как он держит кисть и другие орудия для рисования. Как топор он их держит )) и переучить его пока не могу.. иногда соглашается взять по другому, но оч быстро перехватывает обратно. Поэтому рисует он не кистью руки, а всей рукой, что конечно же неудобно очень… не знаю как его научить держать правильно…

Ни и немного фоток:

разукрашивать учимся (слева мое творчество):

лягушек «прячет»:

рыба-кииит ! тоже «прячет» )) :

один из первых опытов работы с пунктиром .

Дождь нарисовал, можно теперь и боди-артом заняться )) :

а это два в одном , нахождение тени и рисование линий :

ну и под занавес , божьи коровки , тадам:

у меня они честно говоря, вызывают какой то первобытный страх .. прям какие то чужие против хищника ))) но зато совсем сам нарисовал! )

Пирамида карандашом с тенью. Как нарисовать пирамиду карандашом поэтапно

В древности люди были не особо дальновидными и оптимистическими, и вовсе считали, что люди от силы проживут до 2012 года, а потом будут гореть в геенне огенной. Поэтому способности объяснять вещи, или хотя бы намекать на их суть у них не было, в общем, как умения делать вещи простые. Майя сделали постапокалиптический календарь, вызвавший много мух из слона и мыслей о жизни в среднестатистического человека, а египтяне древние построили пирамиды, предназначение которых волнует даже художников. А раз так, мы будем учится как рисовать пирамиды карандашом.

Пирамиды Хеопса — одно из чудес света, куча булыжников, приносящих большой доход от наплыва туристов, а также архитектурный шедевр, построенный еще до нашей с вами эры. В давние времена, за правления бога солнца Ра, их использовали для погребения фараонов, жертвоприношения, платонических контактов с потусторонним миром и других массовых развлечений. Пирамидообразная конструкция как оказалось очень надежная постройка, поэтому подобные здания сооружались и в Месопотамии, Китае, Марсе и Лас Вегасе. Если верить точным источникам из википедии, то пирамиды в Египте называются египетскими, в Китае китайскими и так дальше. Ну вы поняли.

Одно я знаю наверняка, рисовать мистические сооружения куда проще, чем строить, тем более, если делать это по таким шагам:

Как нарисовать пирамиду карандашом поэтапно

Шаг первый. Нарисуйте несколько треугольников, желательно, ровных, а снизу будет песочный фон с верблюдами. Пока что обозначим их окружностями.

Шаг второй. Аккуратно выделите формы пирамид, обведите контуры.

Шаг третий. Теперь добавим несколько бедуинов с верблюдами.
Шаг четвертый. Добавим немного штрихов для правдоподобности. Можно даже раскрасить цветными карандашами. Но это уже оставляю Вам:
Попробуйте нарисовать еще и другие загадочные места нашей планеты.

К азалось бы, что может быть сложного или неправильного в изображении пирамиды? Неужели и здесь репетитор по математике не обходится без специальных приемов и методик? Отмечается всего лишь 4 точки (любые 3 из которых не лежат на одной прямой) и соединяются шестью отрезками. И все. Что здесь обсуждать? Но даже в такой простой ситуации репетитору по математике приходится исправлять ученические ошиби. Даже не столько математические, сколько стратегические. Какие? Рисунок, на котором невозможно рассмотреть или показать элементы пространственного тела, подписать значения величин, на котором не развернуться с дополнительными построениями, лучше переделать. Это должен понимать любой репетитор и в начале курса подготовки к ЕГЭ потратить некоторое время на обучение правилам и культуре чертежа.

Кроме требований к его аккуратности и удобному расположению информации из условия задачи существуют еще и математические законы его выполнения. Рассмотрим их подробнее.

Правило метода изображений.

Метод изображений — отдельный предмет, изучению которого на математическом факультете МПГУ отводится целый семестр. То, что мы рисуем на бумаге – следы от проекций частей тела на некоторую плоскость. От нее зависит то, какие отрезки и какие сечения будут отчетливо видны, а какие окажутся «наползающими» друг на друга или скрытыми. Когда репетитор по математике решает, с какой стороны нарисовать ученику пирамиду, он определяет расположение плоскости и направление проецирования.

Существуют геометрические законы проецирования простейших стереометрических объектов. Длины непараллельных отрезков, например, при изображении могут менять соотношение своих длин (преподавателю лучше произнести «искажаются»). Если в реальности один из них больше другого, то в проекции может быть все с точностью до наоборот. Тоже самое и с углами. Прямой угол может проецироваться как в острый, так и в тупой. Для того, чтобы репетитору математики убедить в этом ученика стоит покрутить перед его глазами обычный угольник. Однако отношение длин отрезков, лежащих на параллельных или совпадающих прямых, не меняется и, в частности, не искажаются середины сторон многоугольников (граней пирамиды). Это объясняет закон расположения основания высоты правильной треугольной пирамиды: оно должно являться точкой пересечения его медиан (центром тяжести). Не искажается также параллельность. Если в пространстве имеется параллельность между прямыми, то она сохраняется и между их следами. Поэтому изображением основания правильной четырехугольной пирамиды выбирается параллелограмм.

Читабельность рисунка.

Важно расположить пирамиду так, чтобы все ее части не просто были видны, а допускали бы дальнейшее усложнение чертежа: проведение апофем, следов от сечений и т.д.

Для этого строить, например, правильную пирамиду желательно снизу вверх через высоту (так она используется почти во всех задачах). Сначала репетитор по математике рисует основание пирамиды, затем ее центр и из этой точки восстанавливает перпендикуляр. Его верний конец выбирается так, чтобы все наклонные ребра были достаточно удалены друг от друга. Если строить в обратном порядке можно промахнуться с центром многоугольника. Конечно, это не критично для решения задач на правильную треугольную пирамиду, но все равно неприглядно для восприятия. Середины должна отображаться серединами.

Построение основания .
Независимо от вида основания тетраэдра его изображают остроугольным треугольником и вытягивают влево или вправо. Зачем? Если он будет равнобедренным, то одно из боковых ребер закроет высоту (если конечно ее основание правильно расположено). Это показано на рисунке.

Фронтальное изображение тетраэдра. Правило репетитора.

Каким краем лучше всего изобразить пирамиду? То есть как оптимально выбрать плоскость для проецирования? Некоторые преподаватели и репетиторы по математике, к сожалению, не обращают внимание на такую «мелочь» как фронтальное расположение пирамиды. А зря. Существует два вида рисунка: «уголком основания к нам» или «уголком от нас» Рассмотрим рисунок с «уголком ABC от нас»:
Восстанавливаем высоту снизу вверх и выбираем положение ее конца (вершины пирамиды) с расчетом на приемлемый размах грани ABP. Для этого самое главное не попасть точкой P на линию AB. Иначе мы грань не увидим. Значительное отклонение от точки пересечения (в изображении) линий AB и OP вызывает довольно небольшое отклонение луча AP от луча AB и поэтому, чтобы добиться размаха грани ABP, необходимо выбирать точку P или очень низко или очень высоко. Последнее может чрезмерно укрупнить рисунок, вытягивая пирамиду вверх (сокращая пространство для самого решения), а низкая точка делает рисунок мелким. Поэтому я не рекомендую репетиторам по математике работать с таким фронтом. Лучше всего перевернуть треугольник ABC уголком к нам.

Заметьте, что теперь положение точки P никак не сказывается на читабельности грани ABP и если не равнобедренный и «сильно остроугольный», а точка О – его центр тяжести (то есть O не на высоте основания), то высота пирамиды не будет закрыта ребром BP ни при каком расположении вершины P.

В этом случае репетитор по математике получает определенную свободу выбора вершины пирамиды, что крайне важно для улучшения читабельности дальнейших построений в сложных задачах.

Прорисовка невидимых линий.
Репетитор по математике, конечно, может обойтись и без пунктиров. Однако что русскому то хорошо, то немцу смерь. Ученику — важно воспринять тело именно с той стороны, с которой его видит репетитор. Особенно при работе с гранями. Я советую преподавателю математики чаще называть грани не по вершинам, а по их естественному расположению: «ближняя», «дальняя», «левая», «правая». Если в голове у ребенка сформируется образ объекта «задом наперед», то возникнут проблемы с описанием хода дополнительных построений, чтением рисунка и даже с объяснением непонятных моментов решений.

о построении четырехугольной пирамиды .
Основание правильной четырехугольной пирамиды следует изображаться в виде параллелограмма. Почему? Конечно, можно так расположить квадрат к плоскости проецирования, чтобы прямые углы сохранились (и мы получим прямоугольник), но тогда апофемы двух ближних граней будут закрывать высоту пирамиды. Другого объяснения сложившимся стандартам изображений я не нахожу.

Александр Колпаков, репетитор по математике в Москве . Подготовка к ЕГЭ .

Египет — таинственная цивилизация. Пирамида без сомнений является одним из главных артефактов этой страны. Когда мы видим на картинках изображение этого сооружения, понимаем, что речь идет об Египте, фараонах, мистике, туристах и путешествиях. Каждый художник в рисунке выражает свои мысли. Поэтому в этом уроке мы научимся геометрически точно изображать многогранник, рисовать статуи у её входа и египетскую природу.

Рисуем карандашом

Для начала мы узнаем, как нарисовать пирамиду карандашом.

Нарисуем треугольник.

Из верхнего угла проведем линию к любой точке на его основании. От того, в каком месте линия будет пересекать основание, будет зависеть итоговый ракурс, с которого зритель смотрит на многогранник.

К отрезку, оставшемуся внизу, построим две линии от правого и левого углов.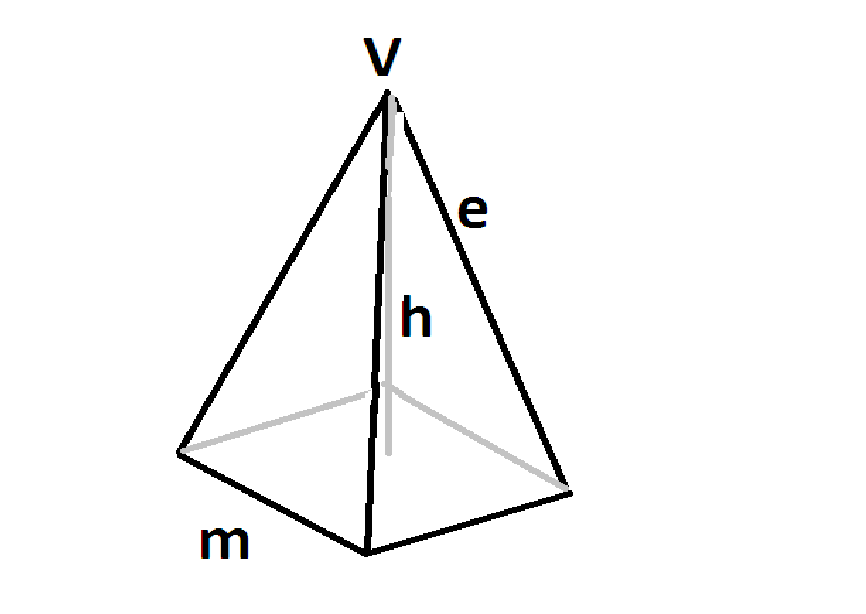

Уберем нижнее горизонтальное ребро, которое находится внутри и зритель не может его видеть. Получится вот так:

Добавим цвет и текстуру, её можно показать образно, в некоторых местах. Так будет понятно, что сооружение сделано из кирпича.

Поэтапный пример

Давайте разберемся, как же поэтапно нарисовать пирамиду? Делается это всего лишь за три шага.

Этап 1
Рисуем основание как и в предыдущем примере.

Этап 2
Стираем ребро невидимой части основания. Обводим готовый контур.

Этап 3
Представляем, какое будет освещение и откуда будет падать свет. Это может быть солнце в пустыне, а может и свет от лампы, который падает на настольную фигуру. Та сторона, на которую падает свет — светлее, в тени — темнее. При более детальной подходе можно наложить тень между камнями монумента.

Египетская пирамида

Теперь посмотрим, как нарисовать египетскую пирамиду. Для этого изобразим её и пейзаж Египта.

Нарисуем основание.

Отметим верхнюю точку. Из углов ромба построим ребра фигуры. Наметим горизонт.

Можно строить так, как указанно в первой части статьи. Для удобства мы изображаем разными способами.

Нарисуем текстуру и песок.

Добавим солнце, небо, рельеф пустыни, тень, которая падает с обратной стороны от солнца. Не забудем о тени на самом сооружении.

Наш рисунок готов.

Гробница Хеопса

Одна из величайших гробниц в Египта. В этой части урока мы узнаем, как нарисовать пирамиду Хеопса на бумаге. Для этого нам понадобится построить пирамиду, вход в неё и статуи по обеим сторонам от дверей.

Рисуем треугольник.

Добавляем перспективу. Подробно, как строить перспективу, показано в первых частях урока.

Рисуем текстуру. Горизонтальные линии кирпича параллельны горизонтальным линиям основы конструкции. В остальном кирпич рисуется, как обычный прямоугольник, только нужно учитывать, что то, что ближе к глазу — больше, а дальше — меньше.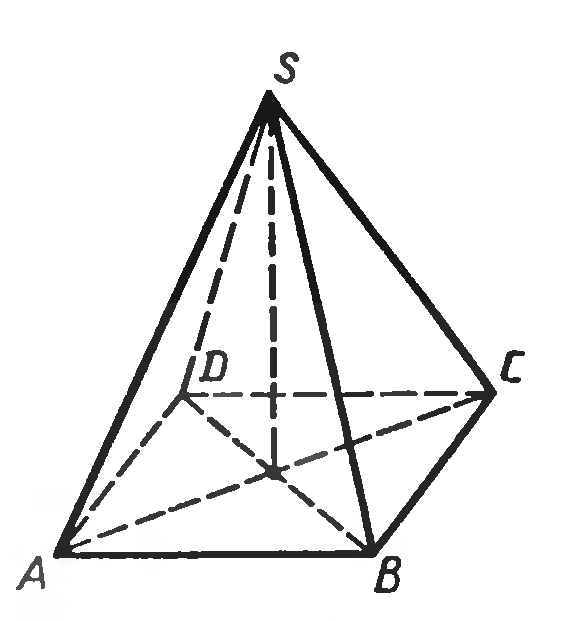

Оставляем свободное место, для того чтобы поместился вход и статуи. Остальное можно обвести.

Строим прямоугольник. После этого две параллельные прямоугольнику линии справа и слева от него. Эти отметки помогут нам при изображении статуй.

Более детально прорисуем вход и статуи.

Нарисуем рельеф пустыни, небо и солнце. Добавим цвет.

Египетский пейзаж

Египетский пейзаж готов!

Треугольная пирамида

Одно из главных особенностей фигуры — это ее правильное построение, это также касается вопроса как нарисовать треугольную пирамиду. В древнем Египте хоронили фараонов, тело которых оставалось таким, как и в первоначальном состоянии после бальзамирования долгие долгие годы. Секрет этого в том, что внутри правильно построенного многогранника замедляются процессы жизнедеятельности.

В заключение этого небольшого пособия мы посмотрим, как нарисовать треугольную пирамиду.

Рисуем фигуру с тремя равными сторонами. Для этого легче всего использовать транспортир. Каждый угол в равностороннем треугольнике равен 60 градусам.

Измерим каждую сторону и поделим пополам. К середине каждой стороны проведем линию из противоположного угла. Отметим точку пересечения трех полученных линий.

Из точки пересечения нарисуем горизонтальную линию, равную высоте полученной линии. Проведем линии от верха треугольника до углов его основания.

А вот так выглядит правильная четырехугольная пирамида.

Если вас интересует, как сделать идеальную по формам и граням пирамиду из бумаги существует определенная схема с размерами, чтобы в итоге получилась правильная фигура. Бумажная пирамида может быть оригинальным подарком, сделанным своими руками или просто интересной поделкой.

Как сделать пирамиду из бумаги. Пошаговая инструкция

Благодаря древнему мастерству оригами есть возможность воссоздавать практически любую фигуру из бумаги, в том числе и пирамиду.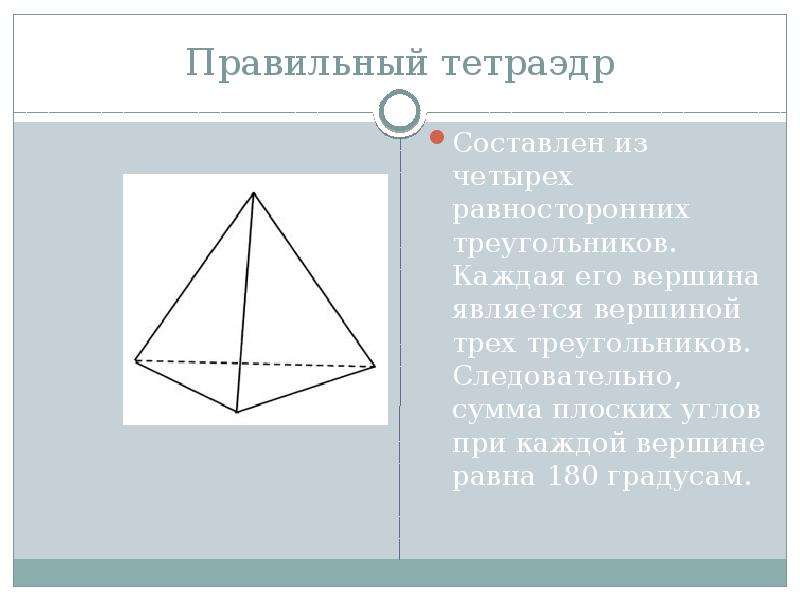 Существует несколько способов, как создать идеальную фигуру с четкими гранями. Для новичков в этом деле есть легкий пошаговый совет, как сделать фигуру из картона. Данная инструкция будет понятна как взрослым, так и детям.

Пошаговое руководство, как склеить пирамиду из картона:

На бумажном листе нужно нарисовать один ровный квадрат и три треугольника. Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.
Ножницами вырезать заготовки не по контуру, а с отступом 3-4 мм, в дальнейшем это будет необходимо при склеивании фигуры.
Смазать клеем все части, дать ему немного подсохнуть и сложить все детали в единую конструкцию.
Дать полностью высохнуть поделке и можно приступить к декору.

Как украсить пирамиду — может быть любая воля фантазии. Например, на нее можно наклеить фигурки, обмотать фольгой или раскрасить специальными акриловыми красками.

Материалы и приспособления

Как сделать пирамиду из бумаги схема с размерами – не единственные главные составляющие в изготовлении фигуры.

Для удобства выполнения оригами следует заранее подготовить необходимые материалы и приспособления, чтобы в момент работы все они были под рукой:

Для изготовления граней могут понадобиться различные материалы. Задействовать можно не только картон, но и пластик, металл, фанеру, стекло или сделать каркас из проволоки. Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией.
Для поделки стоит обзавестись качественным клеем, который можно купить в канцелярском магазине.
Пригодятся острые ножницы, чтобы вырезать ровные заготовки для будущей фигуры.
Также нужны будут линейка, карандаш и ластик на всякий случай .

Для выполнения фигуры не требуется много материалов, все приспособления для пирамиды найдутся почти в каждом доме.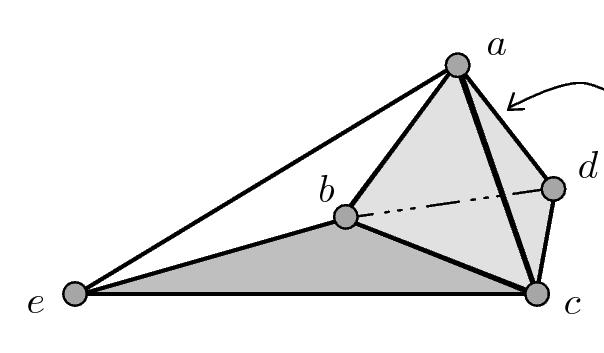

Определяем параметры

Чтобы изделие получилось аккуратным и красивым стоит задать четкие параметры при изготовлении заготовок для будущей пирамиды. Для каждой части может понадобиться отдельный лист бумаги. Можно скачать уже готовые схемы, но их также просто нарисовать самостоятельно.

Главное знать, что ширина треугольника должна быть равна каждой длине грани квадрата.

Высоту геометрической фигуры можно выбрать любую, но рекомендуемая длина, чтобы она была больше на 10-15 см ширины заготовки. Именно при таком соотношении фигура будет смотреться гармонично.

Строим чертеж

Чтобы было проще узнать, как сделать идеальную пирамиду из бумаги или каких-либо других материалов существует схема с размерами. Чертеж – основа для дальнейшего склеивания компонентов для будущей цельной фигуры. Существует несколько видов пирамид, для каждой из них свой чертеж.

Но есть один простой способ, который подходит для детей и новичков в этом деле:

Завершение моделирования

Вырезанную фигуру, нужно склеить по линиям сгибов.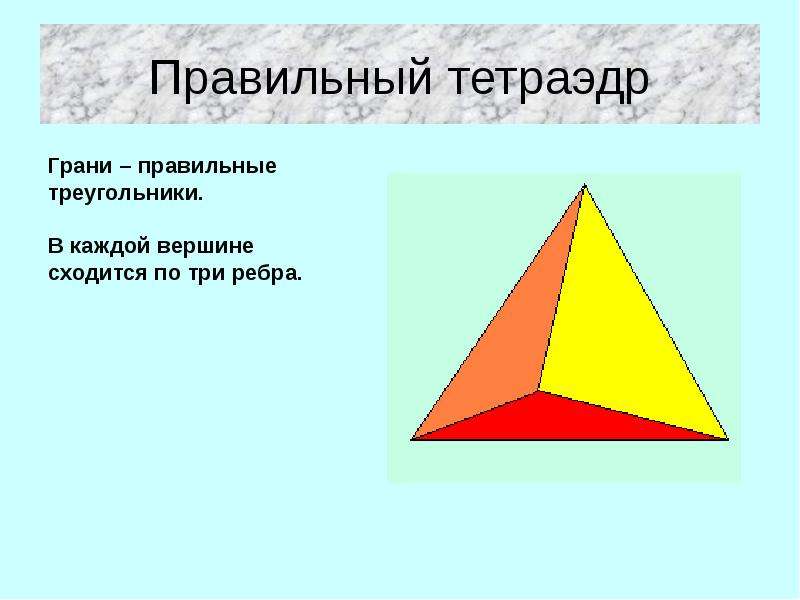 Перед тем как соединить части в полную модель на сгибы нужно нанести клей и немного оставить его застыть, чтобы он лучше схватился. После того как изделие будет готово следует его оставить на полчаса, чтобы потом при оформлении оно случайно не расклеилось. В завершающий этап моделирования входит дизайнерское оформление работы.

Можно разукрасить пирамиду акриловыми или мерцающими красками, нарисовать на ней фигуры.

Изделие можно обклеить фольгой или бумагой для подарков. Также для тех, кто верит в мистическую силу пирамиды стоит на нее приклеить натуральные камни, которые будут подходить под знак зодиака того, кому будет подарена данная фигура. В детском варианте пирамиду можно превратить в животное, приклеив к ней ушки, хвостик и нарисовать черты мордочки.

Способ 2

Такая схема пирамиды подразумевает использование готовой заготовки, которую можно скачать и распечатать на принтере. Этот вариант самый простой, так как не придется чертить фигуры самостоятельно.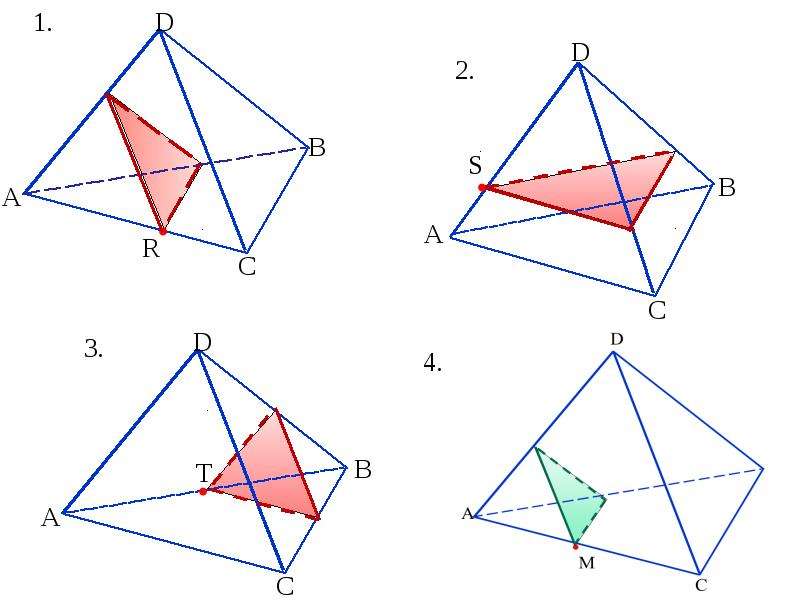 Главное подготовить все необходимые инструменты и оригинально украсить изделие на этапе декорирования.

Способ 3

Существует достаточно много советов, как сделать пирамиду из бумаги, определенная схема с размерами является неотъемлемой частью в выполнении оригами:

Квадратный лист сложить, чтобы углы лежали противоположно друг к другу, лишнюю бумагу отрезать ножницами. Таким способом можно сделать ровный квадрат.
Заготовку свернуть по одной диагонали, раскрыть и свернуть по другой и снова развернуть. Так намечаются нужные линии.
Взять половинки квадрата, свернуть из него треугольник в два слоя. К центру свернуть два угла от основания. Аналогично повторить со второй стороны фигуры.
Согнуть уголки к центру с одной стороны и с другой.
Разогнуть ромб с каждой стороны, уголки его направить внутрь.
Пирамиду нужно выгнуть так чтобы получилась звезда с четырьмя гранями. Фигуру взять двумя руками за разные концы и придать ей форму.

Постепенно придавая объекту форму, начнет получаться пирамида. Очень важно знать, что на последнем этапе нужно действовать аккуратно, стараясь не порвать случайно поделку.

Способ 4

Необходимые инструменты для поделки:

бумажный лист,
треугольник,
ножницы,
карандаш,
клей,
ластик.

Выполнение:

Вырезать квадрат. Согнуть заготовку пополам в разные стороны, чтобы образовались складки.
Диагональ треугольника приложить к каждой из сторон квадрата и по сгибам сделать отметки.
При помощи линий соединить треугольник с вершинами. Для точности рекомендуется использовать линейку.
Отметить карандашом линии склейки сторон.
Фигуру вырезать и нанести клей на линии склеивания.

Как сделать пирамиду из картона?

Сделать фигуру из картона своими руками можно быстро и просто. Использовать можно любую расцветку бумаги, но лучше всего подойдет цвет золота, бежевый, светло-коричневый.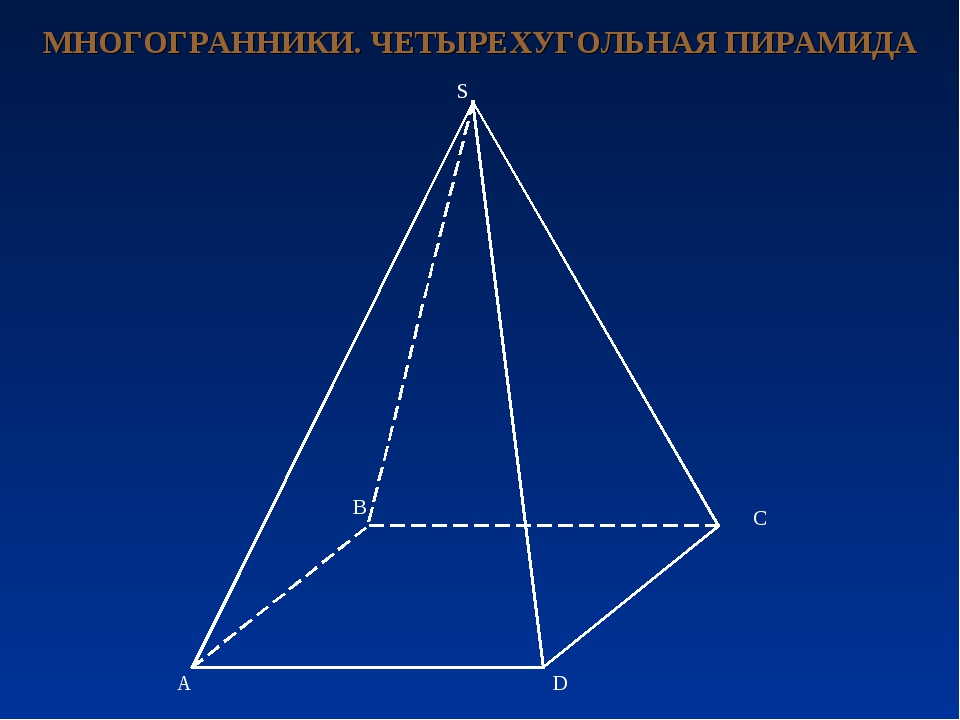

Для того чтобы изделие выглядело более реалистично, то по бумажной заготовке можно произвести линии иголкой горизонтальные и вертикальные.

Благодаря этому будет создаваться эффект реальной мини-пирамиды из Гизы.

По вышеперечисленным пошаговым способам можно создать фигуру с гранями. Картонная пирамида делается по такому же принципу как из простой бумаги.

Но есть большой плюс, что ее можно украсить, например сахарным песком:

Изделие можно покрыть полностью прозрачным клеем и нанести на него сахарный песок. Таким способом можно создать интересный сияющий эффект.
Также пирамиду можно посыпать песком, предварительно обмазав ее клеем. Фигура приобретет эффект реалистичности.

«Золотое сечение» в пропорциях пирамиды

Эталон идеальной пирамиды – определенные правильные пропорции. Ключом к созданию правильной фигуры лежит коэффициент и цифры 7,23. Число, которое имеет значение в науке математике и геометрии, также эти цифры важны в архитектуре и даже медицине.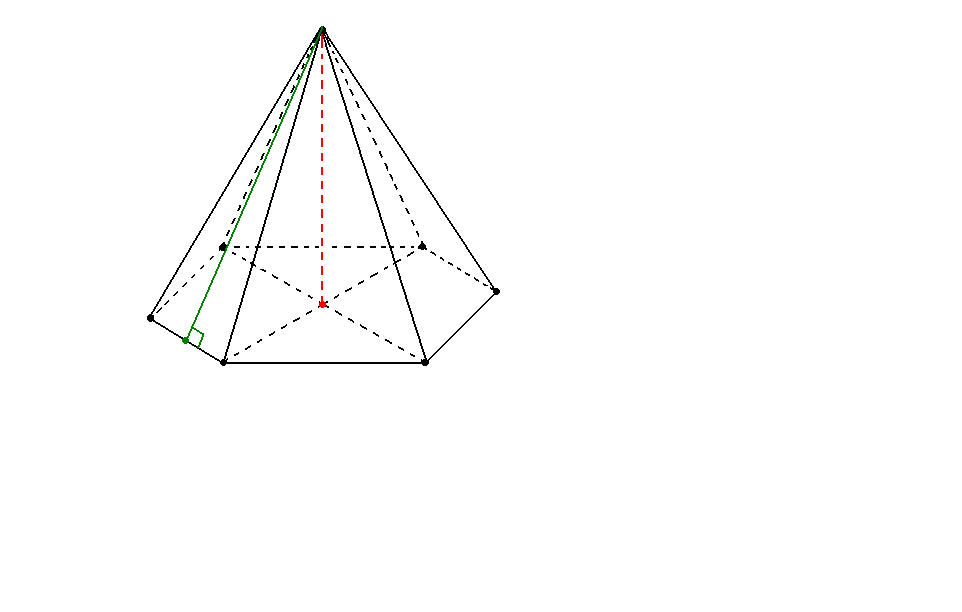

Отрезок длиной 7,23 нужно умножить на коэффициент 1,618. Полученное число 116, 981 следует округлить до 117 см. Эта длина является основанием пирамиды.

Также для получения больших моделей данное число можно умножать в несколько раз. Таким образом, длина нашей пирамиды получается 117 мм, а высота 72 мм.

По теореме Пифагора можно определить длину граней треугольника . Получится число 92,769, его нужно округлить до 93. Эти данные подстроены под идеальную пропорцию «Золотого сечения».

Как сделать развертку четырехугольной пирамиды?

Для изготовления четырехугольной фигуры потребуется:

плотная бумага или картон,
простой карандаш,
линейка,
ножницы,
клей.

Этапы:

Для начала нужно сделать выкройку, в которой основание будет 8 см, а высота 6,5 см.
На листе бумаги нужно нарисовать ровный квадрат, отметить на каждой его грани середину.
Провести из средних точек линии перпендикулярно квадрату, длиной 6,5 см — их всего должно получиться 4.
Из каждой вершины провести по две линии к углам квадрата, так чтобы получились треугольники.
Вырезать заготовку и сложить треугольники так чтобы они сошлись в единую вершину. Склеить фигуру.

Четырехугольную фигуру несложно изготовить самостоятельно. Также на основе этой пошаговой инструкции можно создавать пирамиды больше по размерам.

Как выполнить развертку правильной пирамиды?

Чтобы понимать как сделать пирамиду из бумаги, необходимо знать схему с размерами.

Если интересно как сделать пирамиду с разверткой из бумаги, существует не одна схема с размерами, которая поможет правильно выполнить фигуру. В момент проектирования развертки за основу берется правильный треугольник. Боковая поверхность представлена как плоский чертеж, состоящий из граней и многоугольника.

Для начала определяется натуральная величина основания и истинная величина всех ребер (можно произвести при помощи циркуля). После того как три стороны были найдены строится основание и боковая грань. Берется произвольная точка и из нее проводится дуга равная длине боковых ребер заготовки. На дуге отмечаются четыре отрезка, равные основанию пирамиды.

Все линии соединяются, в том числе с произвольной точкой. К одному из получившихся треугольников пририсовывают квадрат, который равен основанию фигуры.

Сложные фигуры: объемные макеты

Фигуры такого типа делаются для получения навыков в работе с объемными изделиями из бумаги и в целях обучения детей начальным азам геометрии. Из таких моделей можно смастерить оригинальную подарочную упаковку. Иногда бывает сложно разработать правильную развертку, рекомендуется обладать хотя бы небольшими знаниями черчения.

Но существуют готовые трафареты, которые можно будет распечатать с принтера . Макеты используются не только в развлекательных целях, но и в обучающих. Ребенку можно наглядно показывать, как выглядит та или иная фигура. Сложные модели могут быть: куб, октаэдр, додекаэдр, икосаэдр и другие.

Перед тем как начать выполнять черчение фигуры стоит представить ее в 3D формате, сколько она имеет граней и измерений.

На листе бумаги нужно нарисовать грани, так чтобы они между собой правильно соединялись. У каждой фигуры есть свой определенный тип грани. Ребра тоже должны быть одинаковой длины, чтобы при скреплении не появились несостыковки. Если макет имеет одинаковые стороны, то в момент черчения можно нарисовать шаблон и по нему рисовать остальные заготовки.

3D макеты важны при обучении детей: они дают ученикам возможность подержать фигуры в руках, рассмотреть их и лучше понять строение. Также при изучении некоторых теорем (Эйлера) рекомендуется наглядное пособие.

Моделирование различных многогранников

Чтобы научиться выполнять более сложные модели, стоит начать с азов, например, с 3D треугольников. Постепенно улучшая навык в создании простых макетов можно приступить к сложным моделям. Сложные фигуры требуют навыков и отточенной сноровки при выполнении, например в момент развертки или придавания формы фигуре, нужно действовать так чтобы она случайно не порвалась.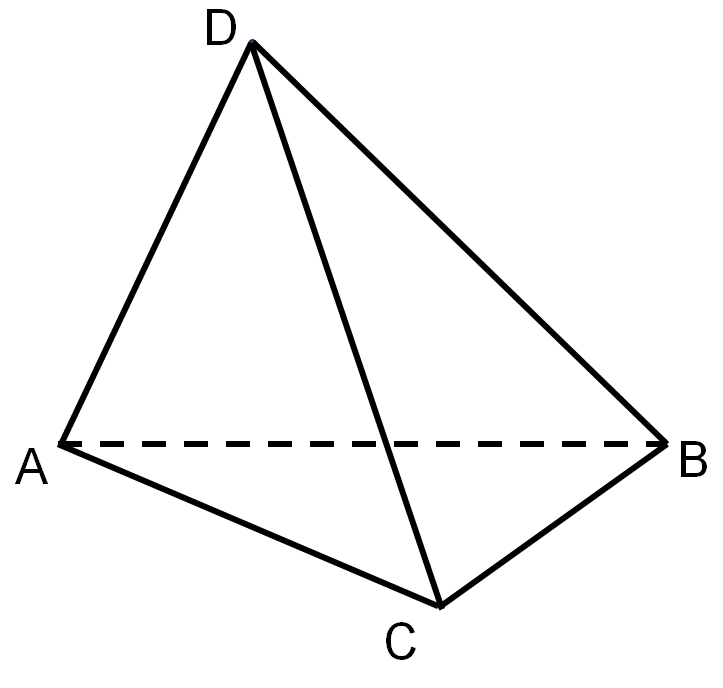

При выполнении чертежа следует внимательно наносить разметки и уметь рисовать фигуры.

Если есть вопрос, как сделать качественную пирамиду из бумаги, существует подробная схема с индивидуальными размерами. Стоит лишь приложить немного усилий, и тогда составит труда выполнить красивую и качественную работу, которая будет радовать глаз.

Благодаря вышеперечисленным способам можно легко создать различные макеты пирамид. Не сложно научиться выполнять эти техники, главное соблюдать все этапы постепенно и внимательно.

Видео о том, как сделать пирамиду из бумаги

Как сделать пирамиду из бумаги, узнайте в видео-ролике:

Схема выполнения объемной пирамиды:

Пирамида. AutoCAD 2010

Простое моделирование Монте-Карло для решения математической задачи конкурса Путнэм

Дата публикации Jun 5, 2019

фотоДжонатан ПетерссоннаUnsplash

Есть две вещи, общие для азартных игр с высокими ставками и скоростных гонок — огромная степень неопределенности и город Монте-Карло. Эта связь между этими двумя факторами привела к использованию термина «симуляция Монте-Карло» для вычислительных методов, которые предсказывают вероятности различных результатов процесса, связанных с неопределенностью, с использованием статистической выборки. Смущенный? Не волнуйся! Мы рассмотрим проектирование и выполнение простого моделирования Монте-Карло с использованием Python.

Мой обычно скучный поезд на поезде стал захватывающим, когда один из моих друзей бросил мне вызов, чтобы решить проблему с престижнойКонкурс Путнам- тест, который ставит в тупик даже самых умных студентов по математике там.

Проблема была в следующем (перефразирован):

Если вы выбираете 4 случайные точки на сфере и присоединяетесь к ним, какова вероятность того, что полученный тетраэдр содержит центр сферы?

Теперь, безусловно, можно установить точное решение, применив несколько концепций геометрии и вероятности. Я ожидаю, что математические гении среди вас будут готовы ответить до того, как вы закончите читать это предложение. Для тех из вас (как я), которые не могут,видео3Blue1Brown на YouTube дает довольно элегантное объяснение аналитического решения.

Однако слово «случайный» в этой проблеме вызвало в моей голове альтернативный ход мыслей, что в конечном итоге привело к решению, которое я собираюсь представить. Я рассмотрел возможность получения решения черезслучайная выборка, Идея была проста — нарисовать большое количество случайных выборок тетраэдров и рассчитать вероятность с учетом всех этих выборок.

Широкий алгоритм моделирования выглядит следующим образом:

Определить поверхность сферы известного радиуса как образец пространства.
Определите результирующую вероятность как num / den, где num = 0 и den = 1.
Нарисуйте один образец тетраэдра внутри сферы из пространства образцов.
Определите, находится ли центр внутри тетраэдра.
Рассчитайте результирующую вероятность, добавив 1 или 0 к num, основываясь на успехе или неудаче текущего испытания, соответственно, и добавив 1 к den в любом случае.
Повторите шаги с 3 по 5 для указанного количества случайных выборок, которые будут выбраны.
Показать результирующую вероятность.

Мы пройдемся пошагово по коду и подробно рассмотрим каждый шаг.

Шаг 1: Импортируйте необходимые модули

Сначала мы импортируем необходимые модули в Python, а именно:SciPyа такжеMatplotlib,SciPyимеет подмодуль, который позволяет генерировать случайные числа.

import scipy as sci
import matplotlib.pyplot as plt

Шаг 2: Определите образец пространства

Следующий шаг включает создание образца пространства, состоящего из заданного количества точек. Для этого примера, пусть образец пространства10000 балловна поверхности сферы, имеющей радиус1 единица.

Как мы можем гарантировать, что точки на выборочном пространстве лежат на сфере? Три простых шага:

Выберите любой случайный трехмерный вектор, используяsci.random.rand(1,3),Это даст 3D вектор с центром около 0,5, где каждая координата имеет значение от 0 до 1.
Вычтите 0,5 из каждой координаты, чтобы она стала центрирована вокруг 0.
Рассчитайте норму (или величину) вектора и разделите вектор на его норму, убедившись, что он становитсяединичный вектор, Любой единичный вектор обязательно будет лежать на сфере радиуса 1.

Условие if, обеспечивающее, чтобы векторы с нормами, равными 0 или больше 1, не подвергались этому преобразованию, может быть добавлено для безопасности.

Эта анимация была создана с помощью matplotlib; код для этого не приведен в статье. Это просто используется с целью представления скрытых вычислений.

points=10000 #Number of points 
x=sci.zeros((points,3)) #To store x-coordinates of sample points
y=sci.zeros((points,3)) #To store y-coordinates of sample pointsfor i in range(points):
vector=sci.random.rand(1,3)-0.5
if(sci.linalg.norm(vector)!=0 and sci.linalg.norm(vector)<=1.0):
x[i,:]=vector
y[i,:]=x[i,:]/sci.linalg.norm(x[i,:])

Чтобы быть абсолютно уверенным, что все точки в пространстве образца лежат на поверхности сферы, мы можем добавить еще однуконтрольно-пропускной пункт.

Мы вычисляем разницу между фактическими нормами векторов в пространстве образца и желаемой нормой (равной радиусу сферы; здесь 1) и сравниваем ее с допуском (произвольно определенным; здесь 1 × 10⁻¹⁰). Нормы, которые не соответствуют желаемой норме, хранятся вdanger_array, Если размерdanger_arrayравен 0 (то есть, нежелательных норм не существует), затем мы отображаем сообщение «All Clear» и продвигаемся вперед.

y_norms=sci.zeros(points) #Array to store norms of sample vectorsfor i in range(points):
y_norms[i]=sci.linalg.norm(y[i,:])
tol=1e-10 #Tolerance
norm_diff=abs(y_norms-1) #Diff. between actual and desired norm
danger_array=y_norms[norm_diff>tol]if(len(danger_array)==0): 
print("All Clear")
else:
print("Danger")

Шаг 3: Создайте функции, чтобы определить, находится ли центр внутри тетраэдра

После того, как все проверки пройдены, мы переходим к сути проблемы — определяем, находится ли центр сферы в случайном тетраэдре. Это можно упростить, используя две функции.

Первый проверяет, лежат ли центр сферы и четвертая вершина тетраэдра на одной стороне плоскости, образованной оставшимися тремя вершинами тетраэдра

Вторая вызывает первую функцию для всех четырех граней тетраэдра и определяет, находится ли центр внутри тетраэдра.

СформулироватьCheckSideфункции, мы полагаемся на следующие принципы линейной алгебры:

перекрестное произведениеиз двух векторов даетвектор нормали к плоскости, образованной двумя.
скалярное произведениеиз двух векторов даетВеличина компонента одного из векторов в направлении другого, Если компонент ориентирован в противоположном направлении по сравнению со вторым вектором, скалярное произведение оказывается отрицательным.

Мы используем первый принцип, чтобы найти нормаль к плоскости, образованной любыми тремя вершинами.

Далее мы находим скалярное произведение нормали и вектор, соединяющий четвертую вершину с любой из трех вершин — знак этого скалярного произведения сохраняется.

Наконец, мы находим точечное произведение нормали и вектора, соединяющего центр сферы и любую из трех вершин — знак этого точечного произведения сравнивается с предыдущим, и если онисовпадениетогда можно сделать вывод, что четвертая вершина и центр лежат ната же сторонаплоскости, образованной оставшимися тремя вершинами.

Эта схема облегчит вам визуализацию применения двух принципов

def CheckSide(vertices,point):
t1,t2,t3,t4=vertices
p=point
side_1=t2-t1
side_2=t3-t1
normal=sci.cross(side_1,side_2)    ref_vector=t4-t1
ref_sign=sci.dot(normal,ref_vector)    point_vector=p-t1
point_sign=sci.dot(normal,point_vector)    if(sci.sign(ref_sign)==sci.sign(point_sign)):
return 1
else:
return 0

Если мы применимCheckSideФункционируя на всех четырех гранях тетраэдра, мы сможем точно определить, находится ли центр внутри него. Таким образом, мы определяем новую функциюCheckTetrahedronчто вызываетCheckSideфункционировать четыре раза.

Между каждым вызовом функции мырулонмассив вершин по одному, так чтоCheckSideФункция работает с новым лицом при каждом следующем вызове.

Наконец, значения, возвращаемые всеми четырьмяCheckSideвызовы суммируются, и если они равны4затем центр оказывается лежащим внутри тетраэдра; если нет, он лежит снаружи.

def CheckTetrahedron(vertices,point):
vert=sci.copy(vertices)
check_1=CheckSide(vert,point)    vert=sci.roll(vert,1,axis=0)
check_2=CheckSide(vert,point)    vert=sci.roll(vert,1,axis=0)
check_3=CheckSide(vert,point)    vert=sci.roll(vert,1,axis=0)
check_4=CheckSide(vert,point)    sum_check=check_1+check_2+check_3+check_4    if(sum_check==4.):
return 1
else:
return 0

Шаг 4: Инициализация

Теперь, когда у нас есть все необходимые функции, пришло время перейти к фактическому запуску. Перед тем, как начать прогон, нам нужно инициализировать несколько параметров для прогона и для построения графика.

Массивcheck_pointбудет хранить«0 ‘а также«1 ‘обозначитьуспехилиотказкаждой итерации. Вместо того, чтобы хранить только одно значение результирующей вероятности, мы создадим массив для хранения его значения для каждой итерации, чтобы мы могли построить кривую, которая показывает изменение вероятности в зависимости от количества итераций.

centre=[0,0,0]
number_of_samples=10000
sample_span=sci.arange(0,number_of_samples,1)
check_point=sci.zeros(number_of_samples) 
prob=sci.zeros(number_of_samples)

Шаг 5: Бег

Пришло время запустить симуляцию! На каждой итерации мы делаем следующие три вещи:

Выберите 4 разных случайных точки из выборочного пространства.
ПрименитьCheckTetrahedronфункционировать в эти 4 точки и центр, чтобы определить, находится ли центр в тетраэдре, образованном этими 4 точками.
В зависимости от успеха или неудачи испытания, сохраните 1 или 0 соответственно вcheck_pointи обновить значение результирующей вероятности вprobмассив.

Эта анимация была создана с помощью matplotlib; код для этого не приведен в статье. Это просто используется с целью представления скрытых вычислений.
for i in range(number_of_samples):
indices=sci.random.randint(0,points,4)
vertex_list=y[indices]
check_point[i]=CheckTetrahedron(vertex_list,centroid)
prob[i]=len(check_point[check_point==1.])/(i+1)
Шаг 6: Построение графика
Наконец, пришло время построить результаты и выяснить результирующую вероятность после запуска симуляции для заданного числа итераций. Мы добавляем несколько наворотов к сюжету, чтобы он выглядел привлекательно, а также чтобы он четко и четко передавал всю необходимую информацию.
#Plot blank figure
plt.figure(figsize=(15,10))#Plot resultant probability from simulation
plt.plot(sample_span,prob,color="navy",linestyle="-",label="Resultant probability from simulation")#Plot resultant probability from analytical solution
plt.plot(sample_span,[0.125]*len(sample_span),color="red",linestyle="-",label="Actual resultant probability from analytical solution (0.125)")#Plot value of final resultant probability in text
plt.text(sample_span[int(number_of_samples/2)],0.05,f"The final probability is {prob[-1]:.4f}",fontsize=16)#Display axis labels
plt.xlabel("Number of iterations",fontsize=14)
plt.ylabel("Probability",fontsize=14)#Display legend
plt.legend(loc="upper right",fontsize=14)#Display title of the plot
plt.title("Variation of resultant probability with increase in the number of iterations",fontsize=14)
Окончательный сюжет приведен ниже. Из характера сюжета совершенно ясно, чтовероятность сходится к истинному значению (то есть аналитическому решению) по мере увеличения числа итераций.
График, созданный с помощью matplotlib, подробно описывает изменение вероятности в зависимости от количества итераций.
Заключительные мысли
Вполне возможно, что ваша симуляция может не сходиться к истинному значению за то же число итераций, что и моя, из-за связанной случайности в методе. В этом случае вы можете продолжать увеличивать количество итераций, пока ваше решение не приблизится к истинному значению.
Аналитическое решение1/8или0,1250и моделирование Монте-Карло сходится к значению0,1248,что достаточно близко. Мы создали очевидный порядок случайности с помощью моделирования — тот факт, что повторяющаяся случайная выборка может привести к единому конвергентному решению, поразителен. Этот метод может показаться неэффективным — почти как использование вычислительной мощности методом грубой силы — но он очень эффективен и дает точные ответы.
Код был задокументирован и выполнен вБлокнот Jupyterэто можно посмотреть онлайн.
Я надеюсь, что смог объяснить метод и код с ясностью. Вы можете ответить в комментариях, задать вопросы или высказать любые предложения, которые могут у вас возникнуть.
Вы также можетеследуйте за мной в Twitter здесь.
Оригинальная статья
как из бумаги сделать тетраэдр
Если вдруг вам дали задание на уроке геометрии или само по себе возникло желание освежить в памяти свойства объемных фигур, то вам непременно следует прочесть о том, как из бумаги сделать тетраэдр, и обязательно применить наши советы на практике. Ведь эта фигура благодаря своей простоте является одной из базовых моделей трехмерного моделирования.
Само слово «тетраэдр» можно перевести с греческого как «четырехгранник». И правда, рассматриваемый объект имеет четыре треугольные грани, а также четыре вершины и шесть ребер. Существует несколько подвидов данной фигуры, но мы не будем обсуждать все возможные варианты. В этой статье вы сможете узнать о способах, как из бумаги сделать тетраэдр. Это будет правильный тетраэдр, все грани которого являются равносторонними треугольниками.
Для работы не понадобится вдаваться в сложные математические вычисления, не придется рассчитывать ни обьем тетраэдра, ни его площадь, ни высоту. Единственное, что потребуется, — это лист бумаги, карандаш, ножницы и клей, а то и восве можно обойтись только бумагой.
Так как из бумаги сделать тетраэдр, имея все необходимые материалы? Существует несколько способов. Первый и самый распространенный вариант: вырезать четыре отдельных треугольника с так называемыми «лепестками», которые затем склеиваются между собой. Вы можете нарисовать равносторонний треугольник самостоятельно или же воспользоваться готовым шаблоном. К преимуществам этого способа можно отнести возможность сделать фигуру разноцветной, взяв бумагу разных цветов и оттенков. Это придаст изделию яркость и более интересный вид.
Второй способ заключатся в склеивании не отдельных треугольников, а уже соединенных между собой (так называемая развертка тетраэдра). В этом случае тоже может быть несколько вариантов, а именно: лепестки для склейки могут находиться на всех открытых гранях или же только на некоторых, тех, которые представляют минимум для надежной фиксации.
И, наконец, рассматривая третий способ того, как из бумаги сделать тетраэдр, мы увидим, что нет нужды даже в каких-либо клеящих веществах, ведь еще одним вариантом сборки данной геометрической фигуры является модульное оригами. Вот такую полую пирамиду можно сделать, применив данный метод, имея в запасе достаточное количество бумаги, усидчивости и терпения. В целом, это не очень сложная, но довольно кропотливая работа, и в этой статье мы не будем приводить подробных инструкций. Если вас заинтересует данная информация, вы сможете найти ее в источниках, посвященных этому японскому искусству. И, если вы все-таки дадите себе труд разыскать инструкцию к этой поделке, в скором времени у вас легко получится даже такая сложная конструкция.
Каждый из перечисленных выше вариантов имеет свои преимущества перед остальными, и все они являются достойными и эффективными. И выбирать способ, который подходит именно вам, следует, опираясь на наличие времени и терпения, а также предназначение будущей модели тетраэдра.
Как правильно рисовать геометрические фигуры. Рисование геометрических фигур
Этот урок входит в состав начального комплекса заданий в . С рисования геометрических фигур начинается знакомство с основными законами и правилами академического рисунка.
Для постановки выбирается одна, две или три геометрические фигуры, например, куб, цилиндр или гипсовая ваза с простым сечением. Предметы изображаются на белой предметной плоскости, на светлом фоне. Акцент делается на изображении фигуры, исключая проработку окружающего пространства. Освещение устанавливается сверху и слева от предметов для наглядного строения классических объемов и большей разницей между светом и тенью, что на первых этапах обучения имеет большое значение для анализа формы и передачи тональных градаций на листе.
Цель рисования геометрических фигур.
Научиться компоновать предметы на листе;
Освоить базовые навыки построения и формообразования предметов на плоскости;
Получить представление о перспективном расположении, сокращении линии горизонта;
Приобрести навыки работы карандашом, класть штрих по форме, использовать тона и полутона, грамотно передавать расположения планов.
Для работы с последующими заданиями программы, пригодятся все используемые здесь приемы и техники. Главным итогом этого задания, безусловно, является умение располагать предметы в пространстве. Ваш рисунок станет отражением пространства на листе, где все подчинено неизменным законам композиции и расположению светотени на предметах.
Примеры рисунков простых геометрических форм, выполненных учениками нашей школы.
Это основное и важное задание, где на простом примере, без нагромождения предметов и тонов, ясно демонстрируются конструкция и принципы построения ключевой формы, которая лежит в основе большинства вещей — куб. Эта простая геометрическая фигура содержит в себе основу для создания любого предмета.
Работы выполнены .
Научившись правильно строить и изображать углы, грани и плоскости кубика, точно изображать перспективное сокращение, верно определять точки схода, моделировать штрихом объем и тени, вы сможете интуитивно представлять конструкции и объемы любых предметов. Не просто так в основе трехмерного моделирования сложнейших конструкций всегда находиться куб, как база для создания любой последующей формы. А для рисования куб — это воплощение трехмерного изображения; при рисовании его на листе линиями показывается вертикаль как высота, горизонталь как ширина и третья линия как глубина, которая раскрывает пространство, делая предмет объемным.
Сложно переоценить важность этого задания. Пусть не отталкивает простота постановки, так как в ней содержится фундаментальный принцип создания художественных произведений: от простого к сложному.
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы . Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет) . Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…
Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов . Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности . То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке .
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Объемные рисунки 3d — это новое направление в уличной живописи (граффити). Потрясающие воображение фантастические иллюзии под ногами, стирающие грань между изображением и реальностью. Неудивительно, что это современное искусство так быстро приобрело широкий круг поклонников. Оно популярно не только среди изумленных наблюдателей, но и среди начинающих художников-любителей, каждый из которых, наверное, задавался вопросом: 3d рисунки. Здесь стоит запомнить первое важное правило — даже самые впечатляющие шедевры 3d живописи появлялись сначала на бумаге, и только после этого обретали свое место на городских улицах.
Чтобы научиться создавать изображения объемных фигур на плоской поверхности, пригодятся знания из школьной программы по наглядной геометрии, и поможет эта статья, из которой вы узнаете, как рисовать 3d рисунки на двух видах поверхности: на бумаге и на асфальте.
1.Берем обычный лист бумаги, НВ-карандаш, ластик. На листе рисуем для начала самые простые например, пусть это будут треугольник, круг и квадрат. Теперь, вспоминая уроки геометрии (проецируя рисунки в трех осях координат), превращаем эти фигуры в геометрические тела: конус, сферу и куб соответственно.
2. Второе правило, которое нужно усвоить для того, чтобы понять, как рисовать 3d рисунки — это игра света и тени. Ведь в первую очередь тень, отбрасываемая фигурой, делает эту фигуру визуально объемной. Теперь, используя второе правило, выбираем сторону, откуда будет падать свет на наши нарисованные предметы. И, исходя из этого, начинаем их затенять, помня, что та сторона фигуры, которая находится ближе к предполагаемому источнику света, будет более светлой, чем противоположная. В процессе затенения продвигаемся от темной стороны к светлой. Если вы решите направить источник света спереди от рисунка, тогда оставляйте середину предмета светлой, постепенно, равномерно затеняя фигуру к контурам. После этого рисуем отбрасывание теней. Тени от фигур всегда будут падать с противоположной от света стороны.
3. Освоив эти первые уроки и уяснив, на примере простых объемных фигур, вы постепенно перейдете к созданию более серьезных и сложных трехмерных изображений. И можно будет уже пробовать разбавлять цветом черно-белые рисунки.
4. Научившись технике и овладев необходимыми навыками трехмерного рисования, вы без труда разберетесь, на других поверхностях. Для этого используйте цветные мелки и аэрозольные краски. Подготовленный эскиз на бумаге лучше всего разбить сеткой на небольшие равные квадраты. Так будет удобнее срисовывать, и сетка позволит максимально точно перенести изображение с бумаги на асфальт.
Есть еще несколько хитростей, которые следует запомнить, чтобы понять, как рисовать 3d рисунки на асфальте:
Место под рисунок должно быть как можно более ровным и подготовленным (тщательно расчищенным от возможного мелкого мусора).
Работать над изображением лучше всего в пасмурную или облачную погоду.
И еще, т. к. вам придется растирать мел пальцами (для закрепления), вооружитесь заранее полиэтиленовыми пакетами для защиты подушечек пальцев от истирания.
В процессе работы над рисунком продвигаться нужно сверху вниз. Стоит избегать прорисовывания четких ровных контуров, а цвет фона вашего рисунка должен по возможности совпадать с цветом дорожного покрытия, на котором вы будете работать.
Очень важно также угадать с размерами занимаемой площади, т. к. 3d рисунки имеют вытянутые пропорции и внушительные масштабы. И, конечно, не надо забывать, что изображение будет казаться трехмерным лишь с одной заданной вами позиции.
Итак, теперь вы знаете, как рисовать 3d рисунки на бумаге и асфальте, а нам остается лишь пожелать вам удачи в этом интересном деле!
Очень легко, но это далеко не так. Чтобы изобразить объем и тень, необходимо умение и аккуратность в работе. Рассмотрим, как нарисовать цилиндр карандашом.
Первый вариант
Вариантов рисования карандашом много, разберем поэтапно один из них. Для работы потребуется карандаш, желательно средней мягкости, ластик и лист белой бумаги, можно взять формат А4.
Ход работы:
Нарисуйте две параллельные линии. Сверху и внизу соедините отрезки овалами. Так как это урок рисования, то никаких линеек не используйте, старайтесь сразу ставить руку, чтобы в будущем было легче рисовать различные предметы.
Сделайте две перпендикулярные линии в верхнем овале, а из середины проведите линию вниз.
Снизу также прорисуйте две линии.
Обведите контур более ярко и переходите к выполнению тени.
Выбираем правую сторону для более темного оттенка, с левой стороны цилиндр останется белым. Наносить тень надо аккуратно, растушевывая карандаш. Оттенок должен сменяться очень плавно.
Прорисовываем тень от цилиндра. Так как справа у нас темнее, то изображаем ее спереди.
Точной длины нет, поскольку в разное время суток длина тени от предметов неодинакова.
В данном случае берем около трети высоты цилиндра. Прорисовываем два параллельных диагональных отрезка и соединяем их вершины.
Закрашиваем тень.
Работа готова. Это один из самых простых вариантов, так как мы не использовали перспективы и изобразили только один цилиндр.
Второй вариант
В данном мастер-классе мы рассмотрим, как нарисовать цилиндр карандашом уже на более профессиональном уровне, так что если вы неуверены в своих силах, лучше не браться за работу. А также такая техника графики не подходит для маленьких детей.
Для работы вам потребуются:
бумага, причем для начинающих художников лучше приобрести специальную среднезернистую, на которой значительно приятней рисовать;
несколько карандашей с разной степенью твердости;
ластик;
палочка, чтобы растирать штриховку (можно просто свернуть бумагу в конус и растирать ею).
Совет перед началом творчества: создавать набросок толстыми штрихами, так как их в дальнейшем легче стереть.
Переходим к самой работе, как нарисовать цилиндр поэтапно:
Размечаем лист бумаги. Это необходимо, чтобы правильно определить местоположение фигуры.
Делаем разметку. Для этого прорисовываем две вертикальные линии от руки, слегка нажимая на карандаш. Затем две горизонтальные — сверху и снизу, чтобы соединить прямоугольник.
Следом рисуем пару эллипсов (снизу и сверху) — это основание цилиндра. Чтобы сделать их правильной формы, следует от центра верхней и нижней линии отметить в обе стороны по две точки на одинаковом расстоянии, а затем рисовать фигуру.
Переходим к тонированию. Предположим, что источник освещения располагается сверху справа. И, отталкиваясь от этого, будем прорисовывать самые яркие и темные места.
Самым темным у нас будет передняя сторона, чуть левее центра. Теперь переходим к штрихованию, желательно, чтобы штрихи повторяли форму предмета.
Осталось прорисовать тень от цилиндра, сделаем ее небольшой и в виде конуса зеркально отраженного от цилиндра.
Работа готова. Чтобы скрыть яркость штриховки, берем палочку для затирания или бумагу и плавно проходим небольшими движениями по листу, пока не добьемся нужного эффекта.
Лучше всего оттачивать свое мастерство, прорисовывая реальный объект, поэтому разумнее взять какой-либо предмет для основы. В форме цилиндра много вещей вокруг вас, например, стакан.
Несколько цилиндров
Теперь рассмотрим, как нарисовать цилиндр карандашом с тенью, если мы хотим отобразить сразу несколько объектов.
Поэтапное рисование:
Нарисуйте две опорные точки.
Отступите вниз определенное расстояние и нарисуйте эллипс.
Теперь проведите две вертикальные линии вверх и там тоже прорисуйте эллипс.
Сотрите лишнюю нижнюю линию, у вас получится своеобразная кастрюлька.
Теперь сзади фигуры поставьте две параллельные точки.
Нарисуйте эллипс и от него две линии вниз, причем одну линию только до первой фигуры, а вторую до нужной длины.
Проведите нижнюю изогнутую линию, чтобы закрыть вторую фигуру.
Таким же образом нарисуйте третий цилиндр с другой стороны.
Теперь прорисовываем тень. Она будет справа, так что на всех фигурах более плотной штриховкой закрашиваем правую часть.
Небольшими штрихами в виде прямоугольника от начала изогнутой линии нарисуйте на поверхности тень от предметов.
Ваша работа готова. Мы рассмотрели, как нарисовать цилиндр с тенью, с несколькими элементами на картине.
По такому же принципу можно рисовать много башенок на свое усмотрение, главное, не использовать линейку и не заходить на первые фигуры, чтобы получилась работа объемной.
Рисуем цилиндр на столе
Теперь рассмотрим, как нарисовать цилиндр с окружением. Чтобы правильно все нарисовать, возьмите реальный предмет и поставьте на стол. А свет отрегулируйте так, чтобы тень красиво падала на стол, при этом не была слишком короткой или длинной.
Самый аккуратный рисунок можно сделать на планшете, натянув на него лист бумаги. Подходящий размер этого устройства 30 на 40 см.
Переходим к самому процессу создания рисунка:
Определитесь с расположением фигуры и прорисуйте «невидимые линии» для будущего цилиндра.
Постройте цилиндр, вначале нарисовав две параллельные линии, потом эллипс сверху и снизу.
«Невидимые линии» также потребуются для правильного расположения света и тени. Прорисуйте невидимые грани на лицевой стороне цилиндра, чтобы вы понимали, какие зоны будут темнее, а какие светлее.
Штриховку выполняете по форме фигуры, небольшими линиями, чтобы потом легче было размазывать штрихи.
Заполняете заранее нарисованную тень. Она должна быть темнее.
Теперь необходимо прорисовать плоскость стола и задней стены. Причем задняя стенка будет темнее стола, но светлее, чем основная тень от фигуры.
Таким образом, очень аккуратно и не спеша можно нарисовать объемную фигуру. Необязательно, чтобы это был цилиндр, можно взять шар или куб.
Как нарисовать композицию с несколькими предметами
Чтобы тренироваться в своем мастерстве, используйте сразу несколько фигур. Для начала хорошо подойдет куб, а сверху на него поставьте цилиндр. Отрегулируйте свет, чтобы тень красиво падала на стол, и приступайте к рисованию.
Как нарисовать цилиндр и куб карандашом:
Так как снизу у нас будет куб, то вначале рисуем его на листе бумаги. Чтобы правильно его прорисовать, сначала нарисуйте передний квадрат, а потом линии по диагонали, чтобы придать объем. Соедините сзади линии, затем сотрите лишние грани.
Теперь рисуем цилиндр. Процесс его воссоздания ничем не отличится от предыдущих вариантов, так как куб — это тоже ровная плоскость.
Когда вы расположите фигуры, сотрите лишние грани.
Переходим к теням. Поскольку у нас в прорисовке находится пирамида, то и общая тень у них будет одна в форме башни.
Прорисуйте передние тени на фигурах согласно тому, как у вас падает свет.
Закончите работы задней стенкой и столом.
Такие композиции можно делать самыми разнообразными в зависимости от вашего желания. После того как вы овладеете мастерством рисования геометрических фигур, то сможете рисовать более сложные предметы или композиции.
Чтобы понять, как нарисовать цилиндр правильно, лучше брать за основу реальный предмет, заранее отрегулировав освещение.
Удобнее рисовать на планшете, так как лист не будет скользить.
Используйте карандаши с разной степенью жесткости.
Не спешите при выполнении элементов, а если что-то не получается, не бойтесь начинать сначала.

Рисование геометрических фигур многим может показаться скучным занятием, но на самом деле это базовое упражнение для всех художников. Именно геометрические фигуры помогут разобраться с перспективой, объемом, правильностью формы и композицией. Так что если вы решили заняться академическим рисунком или изобразительным искусством в целом, вам обязательно надо научиться тому, как нарисовать цилиндр, шар, куб, тетраэдр и другие фигуры.

Базовый рисунок цилиндра
Карандаш — это основной инструмент художника. Так что вначале надо научиться тому, как нарисовать карандашом. Ведь именно карандашный набросок является основой для большинства других техник.
Для удобства наметим вертикальную ось, а также две горизонтальных — для верхнего и нижнего овала. Длина верхнего и нижнего овала должна быть одинаковой. Что до ширины, у нижнего она должна быть больше.
На следующем этапе сотрем оси, оставив только основные линии.
Потом наведем контур маркером. Делать это надо аккуратно, чтобы линии были максимально ровными и плавными.
Теперь займемся светом и тенью. Это самый главный этап, ведь именно за счет света и тени появляется объем. Также важно обозначить падающую тень.
Все, мы справились с задачей. Для того, чтобы лучше разобраться и набраться опыта, можно попытаться изобразить и другие геометрические тела: куб, шар, пирамиду и т. д.
Темный цилиндр с бликом
Классическим вариантом изображения геометрических тел является их построение по осям — вертикальным и горизонтальным. Но можно воспользоваться и другим способом — мы опишем его, когда будем учиться тому, как нарисовать цилиндр поэтапно.
Вначале рисуем два овала — верхний и нижний. Обратите внимание — верхний овал более узкий, чем нижний.
Потом соединяем овалы двумя параллельными линиями.
На следующем этапе надо убрать все вспомогательные линии.
Теперь поработаем с тенями. Важно обозначить блик, света, полутени тени и рефлекс (более светлый участок после самого темного участка). Также добавляем падающую тень в стороне, противоположной по направлению к источнику света.
Два цилиндра с тенью
Для того чтобы понять, насколько важна падающая тень в изображении геометрических фигур, давайте разберемся, как нарисовать цилиндр с тенью — легкой и насыщенной.
Вначале обозначим основную форму двух цилиндров. Они будут достаточно низкими.
Потом наведем контуры более насыщенно — для этого отлично подойдет мягкий карандаш.
Начнем прорабатывать тени на левой фигуре. Штриховка должна быть достаточно легкой.
Затем наметим тени на левой фигуре они здесь будут гораздо глубже, насыщенные. Не стоит давить на карандаш — лучше взять помягче.
Все, теперь наше геометрическое тело готово.
Черно-белый цилиндр
Научиться тому, как нарисовать объемный цилиндр и другие фигуры — это основы, без которых начинающему художнику не обойтись. Так что давайте разберемся с этим вопросом.
Как и раньше, начнем с двух овалов — для основания и вершины. Длина должна быть одинаковой, а ширина — отличаться в пользу нижнего, это связано с их положением относительно линии горизонта.
После этого соединим их боковыми линиями. Они должны быть строго параллельны.
Построение сечений тетраэдра. 10-й класс
Цели урока: (Приложение 1, слайды 1-2)
научиться применять аксиомы стереометрии при решении задач;

научиться находить положение точек пересечения секущей плоскости с рёбрами тетраэдра;

освоить методы построения этих сечений

формировать познавательную активность, умения логически мыслить;

создать условия самоконтроля усвоения знаний и умений.

Тип урока: Формирование новых знаний.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
Фронтальный опрос. (Аксиомы стереометрии, свойства параллельных плоскостей)
Слово учителя
Для решения многих геометрических задач, связанных с тетраэдром, полезно уметь строить на рисунке их сечения различными плоскостями. (слайд 3) . Назовём секущей плоскостью тетраэдра любую плоскость, по обе стороны от которой имеются точки данного тетраэдра. Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники. Отметим также, что для построения сечения достаточно построить точки пересечения секущей плоскости с рёбрами тетраэдра, после чего остаётся провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же грани.
На этом уроке вы сможете подробно изучить сечения тетраэдра, освоить методы построения этих сечений. Вы узнаете пять правил построения сечений многогранников, научитесь находить положение точек пересечения секущей плоскости с рёбрами тетраэдра.
Актуализация опорных понятий
Первое правило. Если две точки принадлежат как секущей плоскости, так и плоскости некоторой грани многогранника, то прямая, проходящая через эти две точки, является линией пересечения секущей плоскости с плоскостью этой грани (следствие аксиомы о пересечении плоскостей).

Второе правило. Если секущая плоскость параллельна некоторой плоскости, то эти две плоскости пересекаются с любой гранью по параллельным прямым (свойство двух параллельных плоскостей, пересечённых третьей).

Третье правило. Если секущая плоскость параллельна прямой, лежащей в некоторой плоскости (например, плоскости какой-то грани), то линия пересечения секущей плоскости с этой плоскостью (гранью) параллельна этой прямой (свойство прямой, параллельной плоскости).

Четвёртое правило. Секущая плоскость пересекает параллельные грани по параллельным прямым (свойство параллельных плоскостей, пересечённых третьей).

Пятое правило. Пусть две точки А и В принадлежат секущей плоскости, а точки A₁ и B₁ являются параллельными проекциями этих точек на некоторую грань. Если прямые АВ и A₁B₁ параллельны, то секущая плоскость пересекает эту грань по прямой, параллельной A₁B₁. Если же прямые АВ и A₁B₁ пересекаются в некоторой точке, то эта точка принадлежит как секущей плоскости, так и плоскости этой грани (первая часть этой теоремы следует из свойства прямой, параллельной плоскости, а вторая вытекает из дополнительных свойств параллельной проекции).

III. Изучение нового материала (формирование знаний, умений)
Коллективное решение задач с объяснением (слайд 4)
Задача 1. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є АД, М є ДС, Е є ВС.
Внимательно посмотрим на чертёж. Так как точки К и М принадлежат одной плоскости, то мы находим пересечение секущей плоскости с гранью АДС – это отрезок КМ. Точки М и Е также лежат в одной плоскости, значит пересечением секущей плоскости, и грани ВДС является отрезок МЕ. Находим точку пересечения прямых КМ и АС, которые лежат в одной плоскости АДС. Теперь точка Х лежит в грани АВС, то её можно соединить с точкой Е. Проводим прямую ХЕ, которая пересекается с АВ в точке Р. Отрезок РЕ есть пересечение секущей плоскости с гранью АВС, а отрезок КР есть пересечение секущей плоскости с гранью АВС. Следовательно, четырёхугольник КМЕР наше искомое сечение. Запись решения в тетради:
Решение.
КМ = α ∩ АДС

МЕ = α ∩ ВДС

Х = КМ ∩ АС

Р = ХЕ ∩ АВ

РЕ = α ∩ АВС

КР = α ∩ АДВ

КМЕР – искомое сечение

Задача 2. (слайд 5)
Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є АВС, М є ВДС, N є АД
Проанализируем этот рисунок. Здесь нет точек, лежащих в одной грани. В это случае воспользуемся правилом 5. Рассмотрим проекции каких-нибудь двух точек. В тетраэдре проекции точек находят из вершины на плоскость основания, т.е. М→М₁, N→А. Находим пересечение прямых NM и AM₁ точку Х.Данная точка принадлежит секущей плоскости, так как лежит на прямой NM, принадлежит плоскости АВС, так как лежит на прямой АМ₁. Значит, теперь в плоскости АВС у нас есть две точки, которые можно соединить, получаем прямую КХ. Прямая пересекает сторону ВС в точке L, а сторону АВ в точке Н. В грани АВC находим линию пересечения, она проходит через точки Н и К – это НL. В грани АВД линия пересечения – НN, в грани ВДС проводим линию пересечения через точки L и М – это LQ и в грани АДС получаем отрезок NQ. Четырёхугольник HNQL – искомое сечение.
Решение
М → М₁ N → А

Х = NМ ∩ АМ₁

L = КХ ∩ ВС

H = КХ ∩ АВ

НL = α ∩ АВC, К є НL

НN = α ∩ АВД,

LQ = α ∩ ВДС, М є LQ

NQ = α ∩ АДС

HNQL – искомое сечение

IV. Закрепление знаний
Работа с анимационным объектом «Построение сечения тетраэдра с плоскостью» (диск «Уроки геометрии в 10 классе» урок №16)
Решение задачи с последующей проверкой
Задача 3. (слайд 6)
Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки К є ВС , М є АДВ, N є ВДС.
Решение
1. М → М₁ , N → N₁

Х = NМ ∩ N₁М₁

R = КХ ∩ АВ

RL = α ∩ АВД, М є RL

КР = α ∩ ВДС, N є КР

LP = α ∩ АДС

RLPK – искомое сечение

V. Самостоятельная работа (по вариантам)
(слайд 7)
Задача 4. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВ, N є АС, К є АД.
Решение
КМ = α ∩ АВД,

МN = α ∩ АВС,

КN = α ∩ АДС

KMN – искомое сечение

(Проверка по гиперссылке на Приложение 2)
Задача 5. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВ, К є ДС, N є ДВ.
Решение
MN = α ∩ АВД

NK = α ∩ ВДС

Х = NК ∩ ВС

Р = АС ∩ МХ

РК = α ∩ АДС

MNKP – искомое сечение

(Проверка по гиперссылке на Приложение 3)
Задача 6. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через точки М є АВС, К є ВД, N є ДС
Решение
KN = α ∩ ДВС

Х = КN ∩ ВС

Т = МХ ∩ АВР = ТХ ∩ АС

РТ = α ∩ АВС, М є РТ

PN = α ∩ АДС

ТР N K – искомое сечение

(Проверка по гиперссылке на Приложение 4)
VI. Итог урока.
(слайд 8)
Итак, мы сегодня научились строить простейшие задачи на сечения тетраэдра. Напоминаю, что сечением многогранника называется многоугольник, полученный в результате пересечения многогранника с некоторой плоскостью. Сама плоскость при этом называется секущей плоскостью. Построить сечение значит определить, какие рёбра пересекает секущая плоскость, вид полученного сечения и точное положение точек пересечения секущей плоскости с этими рёбрами. То есть, те цели, которые были поставлены на уроке, решены.
VII. Домашнее задание.
(слайд 9)
Практическая работа «Построить сечения тетраэдра» в электронном виде или бумажном варианте. (Каждому было дано индивидуальное задание).
Нарисуйте тетраэдр на бумаге изометрических точек, математика класса 8 CBSE
Подсказка: Сначала возьмем две точки A, B на изометрической миллиметровой бумаге и соединим AB. В качестве C возьмем точку над AB, а затем соединим AC и BC. Мы берем точку D внутри треугольника ABC и затем соединяем AD, BD, CD. У нас есть искомый тетраэдр ABCD.
Полный пошаговый ответ:
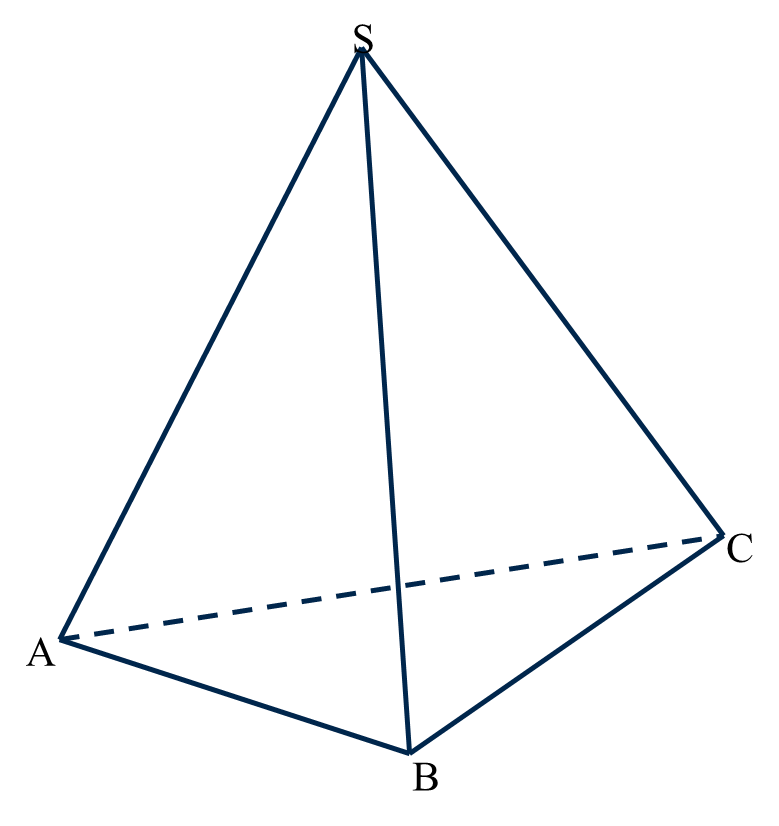
Тетраэдр, иначе известный как треугольная пирамида, представляет собой многогранник, состоящий из четырех треугольных граней, четырех вершинных углов и шести ребер, соединяющих эти четыре вершинных угла.
Изометрическая миллиметровая бумага — это миллиметровая бумага, в которой все точки или точки находятся на одинаковом расстоянии от ближайших точек. Изометрическая миллиметровая бумага, в отличие от обычной миллиметровой бумаги, не имеет сеток.
Берем две изометрические точки на горизонтальной линии с минимальным расстоянием 3 единицы. Назовем их A и B. Эти две точки будут вершинами тетраэдра. Мы присоединились к AB. Отрезок AB будет выступать на краю тетраэдра.

Затем мы берем изометрическую точку как точку, обозначенную буквой C выше или ниже (мы взяли здесь выше), и соединяем BC и AC.Мы получили еще одну вершину C и два других ребра BC и AC тетраэдра.

Мы получили треугольник ABC, который будет выступать в роли треугольной грани требуемого тетраэдра. Возьмем изометрическую точку внутри треугольника ABC. Обозначим эту точку как D. D — четвертая и последняя вершина тетраэдра. Затем мы присоединились к AD, BD, CD.

Мы получили тетраэдр ABCD с вершиной C и треугольным основанием внизу ABD.Шесть ребер — это AB, AC, AD, BC, BD и CD. Треугольные грани — это ABC, ABD, ACD, CBD.
Примечание: Мы также можем нарисовать правильный тетраэдр, у которого длины ребер равны. В этом случае мы должны расположить точку C на серединном перпендикуляре к AB так, чтобы AB = BC = AC. Затем мы размещаем D так, чтобы CD = AD = BD = AB. Фигура или объект рисуется на изометрической миллиметровой бумаге с использованием изометрических проекций. Мы использовали ортогональную проекцию на ребрах, а не на вершинах, чтобы нарисовать здесь тетраэдр.
Тетраэдр — определение, свойства, формулы, примеры
Тетраэдр — это трехмерная фигура с четырьмя треугольными гранями. Один из треугольников считается основанием, а остальные три треугольника вместе образуют пирамиду. Тетраэдр — это разновидность пирамиды, которая представляет собой многогранник с треугольными гранями, соединяющими основание с общей точкой, и плоское основание многоугольника. Он имеет треугольное основание, поэтому его также называют треугольной пирамидой.
Определение тетраэдра
Тетраэдр — это многогранник с 4 гранями, 6 ребрами и 4 вершинами, в котором все грани являются треугольниками.Она также известна как треугольная пирамида, основание которой также является треугольником. Правильный тетраэдр имеет равносторонние треугольники, поэтому все его внутренние углы составляют 60 °. Внутренние углы тетраэдра в каждой плоскости в сумме составляют 180 °, поскольку они треугольные.
Сетка для тетраэдра
В геометрии сеть может быть определена как двухмерная форма, которая при определенном складывании образует трехмерную форму. Тетраэдр — это трехмерная форма, которую можно сформировать с помощью геометрической сети.Возьмите лист бумаги. Обратите внимание на две различные сети тетраэдров, показанные ниже. Скопируйте это на лист бумаги. Обрежьте его по краю и сложите, как показано на рисунке. Сложенная бумага образует тетраэдр.
Свойства тетраэдра
Тетраэдр — это трехмерная форма, которая характеризуется некоторыми отличительными свойствами. На приведенном ниже рисунке показаны грани, ребра и вершины тетраэдра.
Следующие свойства тетраэдра помогают нам легко идентифицировать форму.
У него 4 грани, 6 ребер и 4 вершины (угла).
В правильном тетраэдре все четыре вершины равноудалены друг от друга.
Имеет 6 плоскостей симметрии.
В отличие от других платоновых тел, у него нет параллельных граней.
У правильного тетраэдра четыре равносторонних треугольника на гранях.
Площадь поверхности тетраэдра
Площадь поверхности тетраэдра определяется как общая площадь или область, покрытая всеми гранями фигуры.Он выражается в квадратных единицах, например м ², см ², в ², фут ², ярд ² и т. Д. Тетраэдр может иметь два типа площади поверхности:
Площадь боковой поверхности тетраэдра
Общая площадь тетраэдра
Площадь боковой поверхности тетраэдра
Площадь боковой поверхности тетраэдра определяется как площадь поверхности боковой или наклонной поверхности тетраэдра.Формула для расчета площади боковой поверхности правильного тетраэдра имеет вид
. LSA правильного тетраэдра = сумма 3 равносторонних равносторонних треугольников (т.е. боковых граней)
= 3 × (√3) / 4 a ² квадратных единиц
где a — длина стороны правильного тетраэдра.
Общая площадь тетраэдра
Общая площадь поверхности тетраэдра определяется как площадь поверхности всех граней тетраэдра. Формула для расчета общей площади правильного тетраэдра имеет вид
. TSA правильного тетраэдра = сумма 4 равносторонних равносторонних треугольников (т.е. боковые грани)
= 4 × (√3) / 4 a ² = √3 a ² квадратных единиц
где a — длина стороны правильного тетраэдра.
Объем тетраэдра
Объем тетраэдра определяется как общее пространство, занимаемое им в трехмерной плоскости. Формула для расчета объема тетраэдра имеет вид
. Объем правильного тетраэдра = (1/3) × площадь основания × высота = (1/3) ∙ (√3) / 4 ∙ a ² × (√2) / (√3) a
= (√2 / 12) a ³ кубических единиц
где a — длина стороны правильного тетраэдра.
Темы, связанные с тетраэдром:
Ознакомьтесь с этими интересными статьями, связанными с тетраэдром.
Важные замечания о тетраэдре:
Пять платоновых тел могут быть перечислены как тетраэдр, куб, октаэдр, икосаэдр и додекаэдр.
Тетраэдр — это треугольная пирамида, все четыре грани которой выполнены в виде треугольников.
У тетраэдра 4 грани, 6 ребер и 4 угла.
Часто задаваемые вопросы о тетраэдре
Что такое тетраэдр?
Тетраэдр — это платоновое тело, имеющее 4 треугольные грани, 6 ребер и 4 угла.Его также называют «треугольной пирамидой», потому что основание тетраэдра представляет собой треугольник. Тетраэдр отличается от квадратной пирамиды, имеющей квадратное основание.
Каковы свойства тетраэдра?
Свойства тетраэдра:
У него 4 грани, 6 кромок и 4 угла.
Все четыре вершины одинаково удалены друг от друга в правильном тетраэдре.
В отличие от других платоновых тел, у него нет параллельных граней.
У правильного тетраэдра все грани равностороннего треугольника.
Имеет 6 плоскостей симметрии.
Тетраэдр — это пирамида?
Да, тетраэдр — это разновидность пирамиды, потому что пирамида — это многогранник, основание которого всегда является многоугольником, а другие боковые грани — треугольниками. Поскольку тетраэдр имеет треугольное основание и все его грани являются треугольниками, он известен как треугольная пирамида.
В чем разница между тетраэдром и треугольной пирамидой?
Треугольная пирамида имеет основание в виде треугольника, который не обязательно может быть равносторонним треугольником, тогда как тетраэдр — уникальный случай треугольной пирамиды, в которой все грани являются равносторонними треугольниками.
Является ли квадратная пирамида тетраэдром?
Пирамида с квадратным основанием имеет квадратное основание, а все остальные грани — треугольники, тогда как тетраэдр имеет треугольное основание, а все его грани — равносторонние треугольники. Таким образом, квадратная пирамида — это не тетраэдр.
Что такое основание тетраэдра?
Тетраэдр — это фигура с 4-мя треугольными гранями, поэтому основание тетраэдра также является треугольником.
Как найти объем тетраэдра?
Объем тетраэдра можно рассчитать по формуле (1 / 6√2) s ³ кубических единиц, где s — длина стороны тетраэдра.Он измеряется в кубических единицах.
архивы designcodingtetrahedron — designcoding
Это определение Кузнечика, которое генерирует тетраэдрическую спираль (также называемую спиралью Бурдейка-Кокстера), но забавным образом. Эта геометрия также подходит для касательных сфер. Я сгенерировал спираль, используя компоненты Anemone для рекурсии, и дал ей немного отзывчивости. Я не знаю, зависит ли это от скорости вашего процессора, но если он достаточно медленный, вы увидите игру змейки с тетраэдрической спиралью, поскольку она управляется вашим вводом с ручки управления.В настоящее время я не особо интересуюсь телефонными приложениями, но […]
Тетраэдр — популярное платоническое тело среди дизайнеров. Мы уже объясняли, как рисовать их, используя равносторонние треугольники. Недавно я обнаружил (извините, потерял веб-адрес) гораздо более быстрый способ моделирования тетраэдра с помощью куба. Это очень просто: просто соединение трех противоположных углов куба автоматически делает их равными, в результате чего получаются четыре равные грани. Конечно, на этот раз вам нужно будет вычислить фактическую длину ребра, но если вы воспользуетесь командой «диагональ прямоугольника», у вас также будет возможность установить длину ребра тетраэдра.[…]
Икосаэдр — одно из пяти Платоновых Тел с двадцатью равносторонними треугольными гранями. Это дуальный додекаэдр с пятиугольными гранями. Здесь Икосаэдр построен из пятиугольников. Интересно то, что это близкие отношения с Додекаэдром, хотя они кажутся очень разными. На этот раз мы не будем терять время с рисованием двухмерного пятиугольника. Возможно, мы обсудим это позже. Предполагая, что вы создали правильный пятиугольник, вы должны найти «острие» икосаэдра, пересекая сферы по крайней мере из трех угловых точек с радиусом пятиугольника […]
Усеченный тетраэдр — это твердое тело Архимеда, созданное путем разрезания тетраэдра.Его грани представляют собой правильные шестиугольники и треугольники. Предположим, вы создали тетраэдр, сначала соедините его грани, чтобы создать многоповерхность. Теперь вы можете воссоздать линии ребер тетраэдра, нарисовав их или сгенерировав их (Кривая / Кривая из объектов / Повторяющаяся кромка). Выделив краевые линии, нажмите (Кривая / Точечный объект / Разделить кривую по / количеству сегментов) и введите 3 для количества сегментов, которые необходимо создать. Теперь все края нужно разделить поровну на три части. Нарисуйте равносторонние треугольники, соединяющие […]
Тетраэдр — платоновое тело с 4 равными треугольными гранями (которые также равносторонними), 6 равными ребрами и 4 вершинами.Создавая эту форму, мы более подробно рассмотрим перенос длины с помощью инструментов, подобных компасу, как в двух, так и в трехмерном пространстве. Чтобы определить длину ребра первого треугольника (который является прямой линией), начните с любых двух точек в декартовом пространстве. Используя циркуль (дугу или круг), нарисуйте две дуги (или окружности), используя начальные точки в качестве углов и расстояние между точками […]
Where Else Is A Tetrahedron’s Centroid Edition — nebusresearch
Пару недель назад я прочитал пост из Comics, который вдохновил меня на поиск центра тяжести правильного тетраэдра.Правильный тетраэдр, также известный как «тетраэдр», представляет собой четырехгранную форму штампа. Пирамида с треугольным основанием. Или, если хотите, конус с треугольным основанием. Если попросить человека нарисовать тетраэдр, и он подчинится, он, скорее всего, нарисует эту форму. Центроид, центр масс тетраэдра, находится в точке, которую достаточно легко найти. Он находится на перпендикуляре между любой из четырех граней — равносторонних треугольниках — и вершиной не на этой грани. В частности, это четверть расстояния от грани до другой вершины.Мы можем рассуждать чисто геометрически, без расчетов, и я сделал это в той предыдущей публикации.
Но большинство тетраэдров не правильные. У них тоже есть центроиды; где они?
Книга Бена Зерингера In The Bleachers для 16 марта 2021 года. Этот и другие эссе с участием In The Bleachers собраны по этой ссылке.
Дело в том, что я знаю правильный ответ. Он находится в «среднем» вершинах тетраэдра.Начнем с декартовых координат четырех вершин. Координата x центроида — это среднее арифметическое x-координат четырех вершин. Координата y центроида — это среднее значение y-координат вершин. Координата z центроида — это среднее значение z-координат вершин. Легко рассчитать; но есть ли способ узнать, что это правильный ?
Я могу придумать аргумент, который меня убеждает. В этом смысле у меня есть простое доказательство.Но я также вижу, что этот аргумент оставляет много без внимания. Так что это может никому ничего не доказать. Однако позвольте мне изложить это.
Итак, начните с тетраэдра собственной конструкции. Это будет менее запутанно, если у меня есть метки для четырех вершин. Я собираюсь называть их A, B, C и D. Мне не нравятся эти ярлыки не только из-за банальности, но и потому, что я так хочу, чтобы «C» было названием центроида. Однако я не могу найти способ сделать это, и чтобы четыре вершины тетраэдра не были каким-то странным набором букв.Итак, позвольте мне использовать букву «P» в качестве названия центроида.
Где находится P относительно точек A, B, C и D?
И вот где я даю часть ответа. Начните с размещения тетраэдра в удобном месте. Это был бы пол. Установите тетраэдр так, чтобы грань треугольника ABC находилась в плоскости xy. То есть все точки A, B и C имеют координату z, равную 0. Точка D имеет координату z, отличную от нуля. Позвольте мне назвать эту координату h. Меня не волнует, каковы координаты x и y для любых из этих точек.Что меня волнует, так это то, какова координата z для центроида P.
Свойство центроида, которое было полезно в прошлый раз, заключалось в том, что он разбивал правильный тетраэдр на четыре меньших неправильных тетраэдра, каждый с одинаковым объемом. Каждый из них в четверть объема оригинала. Центроид P делает то же самое и с тетраэдром. Итак, как далеко должна быть точка P от треугольника ABC, чтобы получился тетраэдр с четвертью объема оригинала?
Ответ исходит из того же трюка, который использовался в прошлый раз.Объем конуса равен одной трети площади основания, умноженной на его высоту. Объем тетраэдра ABCD, например, в три раза больше площади треугольника ABC, умноженной на то, как далеко точка D находится от треугольника. Это число я обозначил h. Объем тетраэдра ABCP в три раза больше площади треугольника ABC, умноженной на то, как далеко точка P находится от треугольника. Таким образом, точка P должна быть на одну четверть дальше от треугольника ABC, чем точка D. Его координата z равна четверти часам.
Кстати, обратите внимание, что, хотя я ничего не знаю о координатах x и y любой из этих точек, я знаю координаты z.Все A, B и C имеют координату z, равную 0. D имеет координату z, равную h. А у P координата z равна четверти h. Четверть h наверняка выглядит как среднее арифметическое 0, 0, 0 и h.
На этом я убежден. Координаты центроида должны быть средним значением координат вершин. Но вы также видите, насколько адресован , а не . Вы, вероятно, согласитесь, что я вычислил координату z, когда три вершины имеют одинаковую координату z. Или где три вершины имеют одинаковую y-координату или одинаковую x-координату.Вы можете допустить, что если я могу повернуть тетраэдр, я могу получить три точки с одной и той же координатой z (или y- или x-, если хотите). Но это по-прежнему только одна координата центроида P.
Я уверен, что немного алгебры завершит это. Но я бы хотел этого избежать, если смогу. Я подозреваю, что способ аргументировать это геометрически зависит от знания прямой, соединяющей вершину D и центроид тетраэдра P, если он расширен, проходит через центр тяжести треугольника ABC. То же самое относится и к вершинам A, B и C.Я также подозреваю, что существует связь между вектором, указывающим направление от D к P, и суммой трех векторов, указывающих направления от D к A, B и C. Однако я не совсем понял.
Я дам тебе знать, если подойду ближе.
Нравится:
Нравится Загрузка …
Связанные
Автор: Джозеф Небус
Я родился 198 лет спустя после Джонни Эпплсид. На этом различия между нами не заканчиваются.Он / он. Просмотреть все сообщения Джозефа Небуса
Как найти площадь тетраэдра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.

как рисовать тетраэдр — 3 рекомендаций на Babyblog.ru

Пирамида карандашом с тенью. Как нарисовать пирамиду карандашом поэтапно

Правило метода изображений.

Читабельность рисунка.

Фронтальное изображение тетраэдра. Правило репетитора.

Рисуем карандашом

Поэтапный пример

Египетская пирамида

Гробница Хеопса

Египетский пейзаж

Треугольная пирамида

Как сделать пирамиду из бумаги. Пошаговая инструкция

Материалы и приспособления

Определяем параметры

Строим чертеж

Завершение моделирования

Способ 2

Способ 3

Способ 4

Как сделать пирамиду из картона?

«Золотое сечение» в пропорциях пирамиды

Как сделать развертку четырехугольной пирамиды?

Как выполнить развертку правильной пирамиды?

Сложные фигуры: объемные макеты

Моделирование различных многогранников

Видео о том, как сделать пирамиду из бумаги

Пирамида. AutoCAD 2010

Читайте также

Пирамида автоматизации тестирования

Пирамида конверсии

§ 153. Пирамида Лебедева

Пирамида

Пирамида

Пирамида

Пирамида

Пирамида

Пирамида

Пирамида

Пирамида

Пасьянс «Пирамида»

Простое моделирование Монте-Карло для решения математической задачи конкурса Путнэм

Шаг 1: Импортируйте необходимые модули

Шаг 2: Определите образец пространства

Шаг 3: Создайте функции, чтобы определить, находится ли центр внутри тетраэдра

Шаг 4: Инициализация

Шаг 5: Бег

Шаг 6: Построение графика

Заключительные мысли

как из бумаги сделать тетраэдр

Как правильно рисовать геометрические фигуры. Рисование геометрических фигур

Основные геометрические фигуры:

Упражнения

Первый вариант

Второй вариант

Несколько цилиндров

Рисуем цилиндр на столе

Как нарисовать композицию с несколькими предметами

Базовый рисунок цилиндра

Темный цилиндр с бликом

Два цилиндра с тенью

Черно-белый цилиндр

Построение сечений тетраэдра. 10-й класс

Нарисуйте тетраэдр на бумаге изометрических точек, математика класса 8 CBSE

Тетраэдр — определение, свойства, формулы, примеры

Определение тетраэдра

Сетка для тетраэдра

Свойства тетраэдра

Площадь поверхности тетраэдра

Площадь боковой поверхности тетраэдра

Общая площадь тетраэдра

Объем тетраэдра

Часто задаваемые вопросы о тетраэдре

Что такое тетраэдр?

Каковы свойства тетраэдра?

Тетраэдр — это пирамида?

В чем разница между тетраэдром и треугольной пирамидой?

Является ли квадратная пирамида тетраэдром?

Что такое основание тетраэдра?

Как найти объем тетраэдра?

архивы designcodingtetrahedron — designcoding