Как нарисовать конус в перспективе
В этом пошаговом руководстве объясняется, как нарисовать конус в перспективе.
Прежде чем перейти к этому учебному пособию, вам следует проверить учебник по перспективному рисунку для начинающих, если вы этого еще не сделали.
Шаг 1 – установить основание конуса
Конусное перспективное изображение
Начните рисовать конус, сначала проведя вертикальную линию через то, что позже будет центром фигуры.
Основываясь на этой линии, спроектируйте две симметричные перспективные линии вниз от уровня глаза, чтобы создать квадрат в перспективе.
После завершения этого шага вы можете стереть линии перспективы и верхнюю часть вертикальной линии.
Шаг 2 – Получить центр базы
Конус перспективный горизонтальный центр
От каждого конца основания нарисуйте прямую линию к поперечной. Это должно создать форму «X». Точка пересечения между этими двумя линиями будет серединой конуса.
Шаг 3 – Нарисуйте закругленную форму основания
Конус перспективный круглый базовый рисунок
На предыдущем шаге нарисуйте горизонтальную линию, проходящую через центр «Х», и на основе этой линии нарисуйте две половины округлого основания.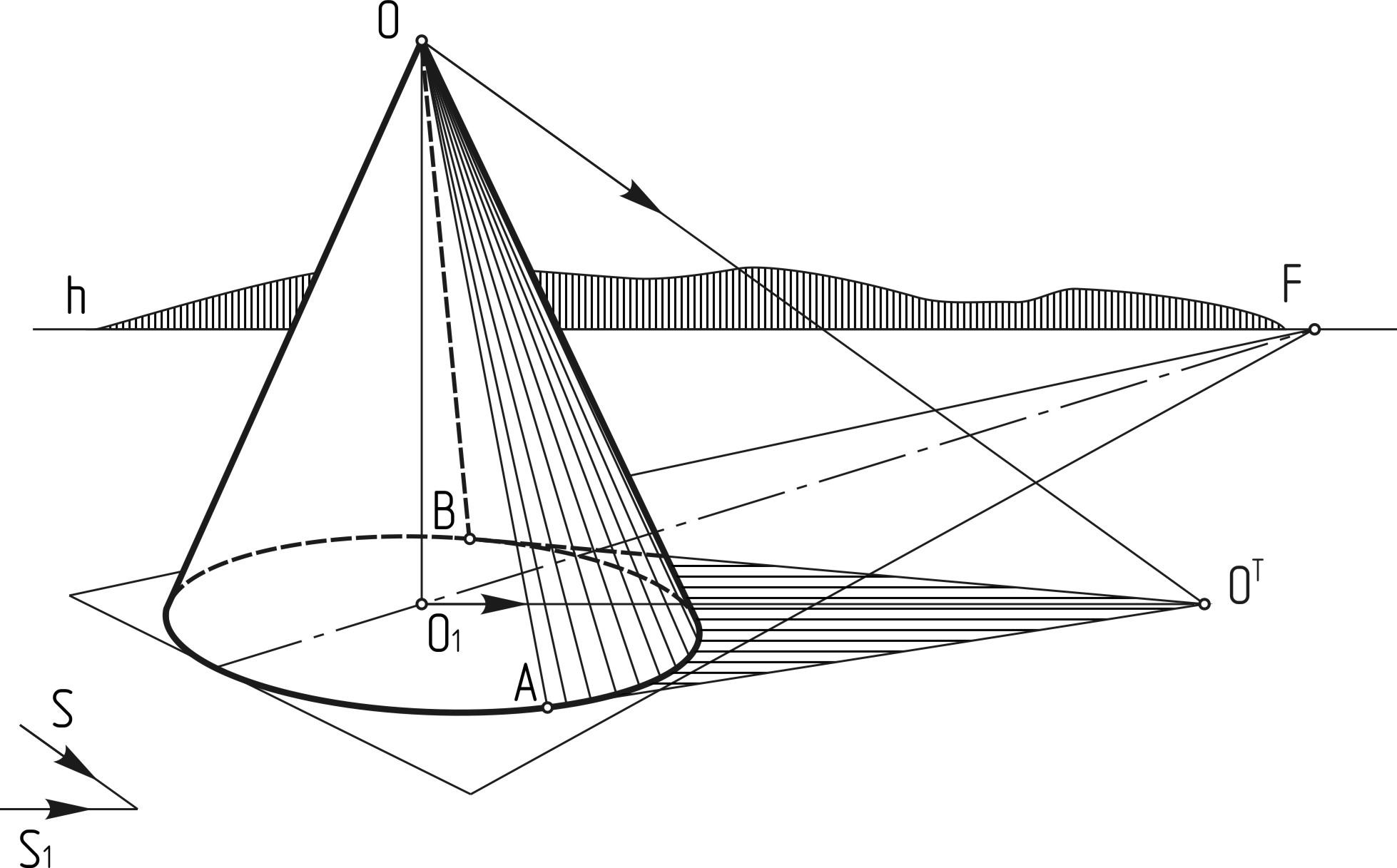 Половина, которая находится ближе к «зрителю», будет больше, чем половина дальней половины.
Половина, которая находится ближе к «зрителю», будет больше, чем половина дальней половины.
Шаг 4 – Нарисуй стороны
Конус, перспективный чертеж строительных сторон
Теперь вы можете нарисовать пару линий, идущих от вертикальной осевой линии к краям круглого основания конуса.
Шаг 5 – Готовый рисунок
Конус увидеть хотя перспективный рисунок
Очистите направляющие линии, и вы должны иметь законченный рисунок конуса. Если вам нужен «прозрачный» рисунок, вы можете оставить видимой дальнейшую часть основания, как в примере выше. Если нет, вы можете стереть скрытую часть базы и сделать простой рисунок линии, как в примере ниже.
Конус в перспективе
Заключение
Конус – очень распространенная форма, поэтому очень полезно иметь возможность нарисовать его в правильной перспективе. Хотя в этом уроке показан только один пример, вы всегда можете отрегулировать высоту и размер в соответствии с тем, что вы рисуете.
Для более основных форм вы можете проверить:
Как нарисовать конус в перспективе
0. 00 (0%) 0 votes
00 (0%) 0 votes
ПОНЯТИЕ О ПЕРСПЕКТИВЕ.
ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ ТЕЛА.
Первое занятие, посвященное объемно-пространственному рисунку. На простейших геометрических телах рассматриваются принципы изображения в перспективе. Это скорее схемы, неоспариваемые «азбучные» истины, которые необходимо запомнить на данном этапе, чтобы, впоследствии не задумываясь, механически применять в работе. Именно поэтому не используются постановочные предметы. Как правило, ученики справляются со всеми заданиями в течение одного учебного дня.
ПОНЯТИЕ О ПЕРСПЕКТИВЕ
Дать понятие перспективного изображения на примере построения остроугольной перспективы параллелепипеда. Рисунок выполняется преподавателем в присутствии ученика поэтапно и сопровождается комментариями.
Материалы: писчая бумага А-4, простые карандаши, ластик.
Этапы
1. Провести линию горизонта (в любом месте писчего листа) и восстановить перпендикуляр (любой длины) ближайшего ребра параллелепипеда, пересекающий линию горизонта.
2. Отметить на линии горизонта две точки схода А и В по разные стороны от ребра-перпендикуляра на любом расстоянии. Соединить концы отрезка, обозначающего ребро параллелепипеда, с точками А и В.
3. Между линиями соединения восстановить еще два ребра на произвольных расстояниях от ближайшего.
4. Соединить концы отрезков, обозначающих ребра с теми точками схода, с которыми они еще не соединены. Например, концы отрезка, ближайшего к точке А соединить с точкой В и наоборот. Точки пересечения вновь проведенных
линий будут являться вершинами последнего четвертого ребра параллелепипеда.
5. Выявить утолщенными линиями получившееся геометрическое тело, считая его прозрачным, причем видимые ребра выделить жирнее. Обозначить вершины параллелепипеда буквами CDEFGKLM.
6. Рассмотреть полученное изображение и отметить, что параллельные в реальной жизни ребра DM, CL, FK, EG сходятся в точке А и на рисунке параллельными не являются. Аналогичная ситуация с другой четверкой ребер DF, CE, MK, LG. Вертикальные же ребра сохраняют свою параллельность и перпендикулярность линии горизонта (так как мы принимаем, что параллелепипед лежит на горизонтальной поверхности и размеры его сравнительно невелики). Сходиться «вертикальные» ребра будут только при отображении длинномерного предмета: например, высотный жилой дом.
. Перпендикулярность относительно линии горизонта будет нарушаться в случае наклона предмета по отношению к горизонтальной плоскости.
. Прежде, чем начать упражнения, посвященные построению геометрических тел, необходимо отметить, что остроугольная перспектива гротескна и в обычной жизни встречается нечасто (перспектива уличной застройки в городском пейзаже, умышленное искажение формы, усиливающее эмоциональное восприятие и т.д.). Однако она наиболее наглядно демонстрирует основное правило перспективы: ближайший предмет (ребро) всегда больше следующего за ним, аналогично фонарным столбам вдоль дороги. Соответственно линии, ограничивающие горизонтальные плоскости или параллельные им,
никогда не параллельны на рисунке и будут иметь соответствующие общие точки схода, т.е. будут сближаться, удаляясь от ближайшего предмета (линии, ограничивающие дорогу и сходящиеся в точке О на горизонте).ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ ТЕЛА
Построение простейших геометрических тел: куб (параллелепипед), цилиндр, конус, «лежащий» цилиндр.
Задание 1
«Куб (параллелепипед)»
По-возможности стараться изобразить куб, хотя, как правило, все равно получается параллелепипед.
Материалы: писчая бумага А-4, простые карандаши, ластик, угольники, линейка.
Этапы
1. Взять лист А-4 писчей бумаги. Начать построение с ближайшего ребра.
2. Далее нарисовать «открытую книжку», учитывая, что пары линий, расположенных по одну сторону от «корешка» обязательно должны сходиться. Рисунок невелик, куб – небольшой предмет, поэтому сближение исчисляется долями миллиметра, но оно необходимо, дабы избежать обратной перспективы, когда предмет «выворачивается» на зрителя, встает дыбом (см. рис. в конце подпункта 5).
. Может возникнуть вопрос: «Почему мы не ищем точек схода и, вообще, не повторяем построения разобранного ранее рисунка?» Дело в том, что это была просто «наглядная картинка», иллюстрация к теории: столь
сложное построение очень редко используется в рисовании малых форм: натюрморты, элементы интерьера и т. п. На основе нее нужно просто понять и запомнить, как аксиому, принципы изображения в перспективе.
п. На основе нее нужно просто понять и запомнить, как аксиому, принципы изображения в перспективе.
3. Восстановить перпендикуляры между линиями, идущими по обе стороны от « корешка», тем самым, обозначив две видимые грани и три вертикальных ребра куба.
. Пока условно принята фронтальная перспектива на ближайшее ребро, поэтому вновь появившиеся ребра будут расположены на приблизительно одинаковом расстоянии от него, а последнее, четвертое, может и вовсе совпасть с ближайшим (см. рис. в подпункте 4). «Фронтальность» заключается в том, что ближайшее ребро расположено «лоб в лоб» к зрителю и, соответственно, две видимые грани куба равны, а линии, их ограничивающие, имеют попарно одинаковые углы наклона относительно ближайшего ребра.
. «Условность» же предполагает, что это все-таки рисунок, а не чертеж, поэтому углы могут оказаться чуть разными, что изменит общий вид изображения.
4. Учитывая основные правила перспективного построения, дорисовать оставшиеся «горизонтальные» ребра куба и, соединив их точки пересечения, получить последнее вертикальное ребро.
Фронтальный рисунок куба
(ребра ближайшее — первое
и дальнее — четвертое совпадают)
На данном этапе преподаватель обязательно должен проверить правильность рисунка. Если есть искажения, неточности (линии расходятся, строго параллельны, вертикальность нарушена и т.п.), ученику выдаются угольник и линейка, чтобы он мог предметно убедиться в ошибке и исправить ее (иногда используя эти же чертежные инструменты).
ПРИМЕРЫ НЕПРАВИЛЬНО ВЫПОЛНЕННЫХ ЗАДАНИЙ
Вертикальные ребра не поддерживают перпендикулярность к горизонтальной оси,
горизонтальные же ребра не «сходятся», а «расходятся»,
направляясь к предполагаемой линии горизонта
Слишком активное схождение горизонтальных ребер
Верхние горизонтальные ребра расходятся
(жирной линией выделено правильное направление ребра)
5. Выделить получившийся рисунок геометрического тела разнотолщинными линиями, сохраняя его прозрачность и не убирая линий построения. Видимые части — ярче, жирнее, невидимые – бледнее и тоньше. Сравнить с рисунком, иллюстрирующим
обратную перспективу, чтобы окончательно развеять сомнения по поводу «параллельности» в жизни и на листе.
Выделить получившийся рисунок геометрического тела разнотолщинными линиями, сохраняя его прозрачность и не убирая линий построения. Видимые части — ярче, жирнее, невидимые – бледнее и тоньше. Сравнить с рисунком, иллюстрирующим
обратную перспективу, чтобы окончательно развеять сомнения по поводу «параллельности» в жизни и на листе.
| Прямая перспектива | Обратная перспектива |
6. Самостоятельно нарисовать несколько кубиков-параллелепипедов (от двух до четырех, в зависимости от того, как будут получаться). Обсудить, при необходимости исправить (желательно по мере выполнения каждого рисунка).
ПРИМЕРЫ
Рисунок В.
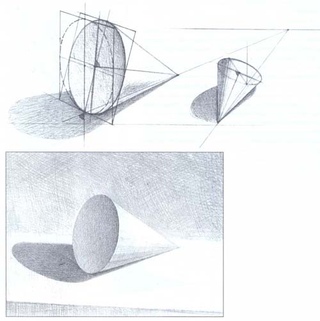 К.
К. Рисунок М.А.
Задание 2
«Цилиндр» Материалы: писчая бумага А-4, простые карандаши, ластик, угольники, линейка.
Этапы
1. На листе А-4 писчей бумаги провести вертикальную ось.
2. Произвольно показать горизонтальные оси, так как предмет строится не с натуры.
3. Отметить на горизонтальных осях точки, симметричные относительно вертикальной оси и соответствующие ширине цилиндра (произвольно).
4. На вертикальной оси, симметрично горизонтальным, отметить еще четыре точки, характеризующие степень раскрытия эллипсов-оснований.
5. В точках, расположенных на горизонтальных осях, нарисовать четыре «скобки».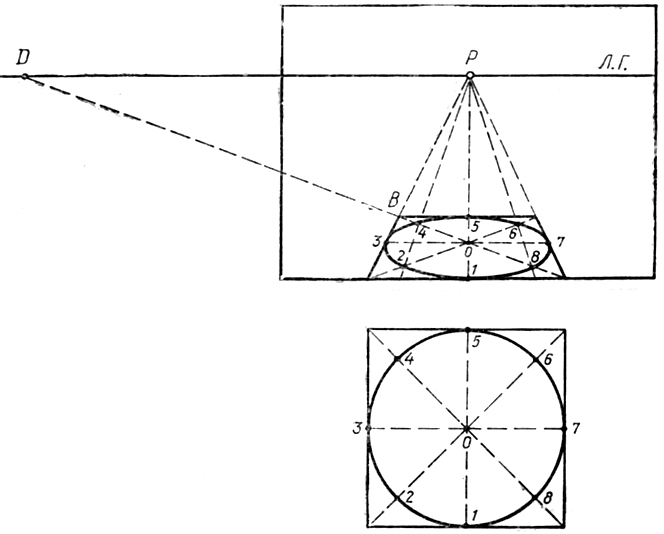
6. Соединить концы «скобок» и точки, расположенные на вертикальной оси. Придать получившимся фигурам форму правильного эллипса.
7. Соединить крайние точки эллипсов, расположенные на горизонтальных осях, вертикальными линиями.
8. Самостоятельно нарисовать несколько цилиндров (от двух до четырех, в зависимости от того, как будут получаться). Обсудить, при необходимости исправить (желательно по мере выполнения каждого рисунка).
ПРИМЕРЫ
| Рисунок Н.Ш. | Рисунок M. A. A. |
. Рассмотренный способ – упрощенный вариант рисования цилиндра, однако он, тем не менее, верен для отображения предметов сравнительно небольшого размера, какие, как правило, и встречаются в различных натюрмортах, бытовых постановках т.п. Но, если быть абсолютно последовательным в вопросах перспективы, то «стоящий» цилиндр, требуется вписывать в «стоящий» параллелепипед.
. В таком случае точки, расположенные над горизонтальными осями, будут к ним ближе, чем расположенные ниже (перспективное сокращение расстояний).
. Степень раскрытия верхнего эллипса уменьшится по сравнению с нижним. И вообще, они превращаются в сложные геометрические фигуры – «неправильные» эллипсы.
. Однако все эти нюансы бывают явными лишь при изображении большеразмерных предметов, например, заводская труба или колонна здания. Поэтому нецелесообразно загружать ученика знанием академического метода, излишне усложняющем
процесс построения на данном этапе. Если только он сам не проявляет активного интереса к этой проблеме.
Поэтому нецелесообразно загружать ученика знанием академического метода, излишне усложняющем
процесс построения на данном этапе. Если только он сам не проявляет активного интереса к этой проблеме.
Задание 3
«Конус»
Материалы: писчая бумага А-4, простые карандаши, ластик, угольники, линейка.
Задание можно предложить для самостоятельного выполнения по аналогии с построением цилиндра. При этом преподаватель должен внимательно отслеживать этапы работы: вертикальная ось, горизонтальная, построение эллипса, точка вершины и соединение ее с полученным основанием конуса. При нарушении последовательности надо вмешаться и поправить рисующего. После первого опыта следует сделать еще пару рисунков геометрического тела. Обсудить, если требуется, исправить (желательно по мере выполнения каждого рисунка).
Рисунок Н.
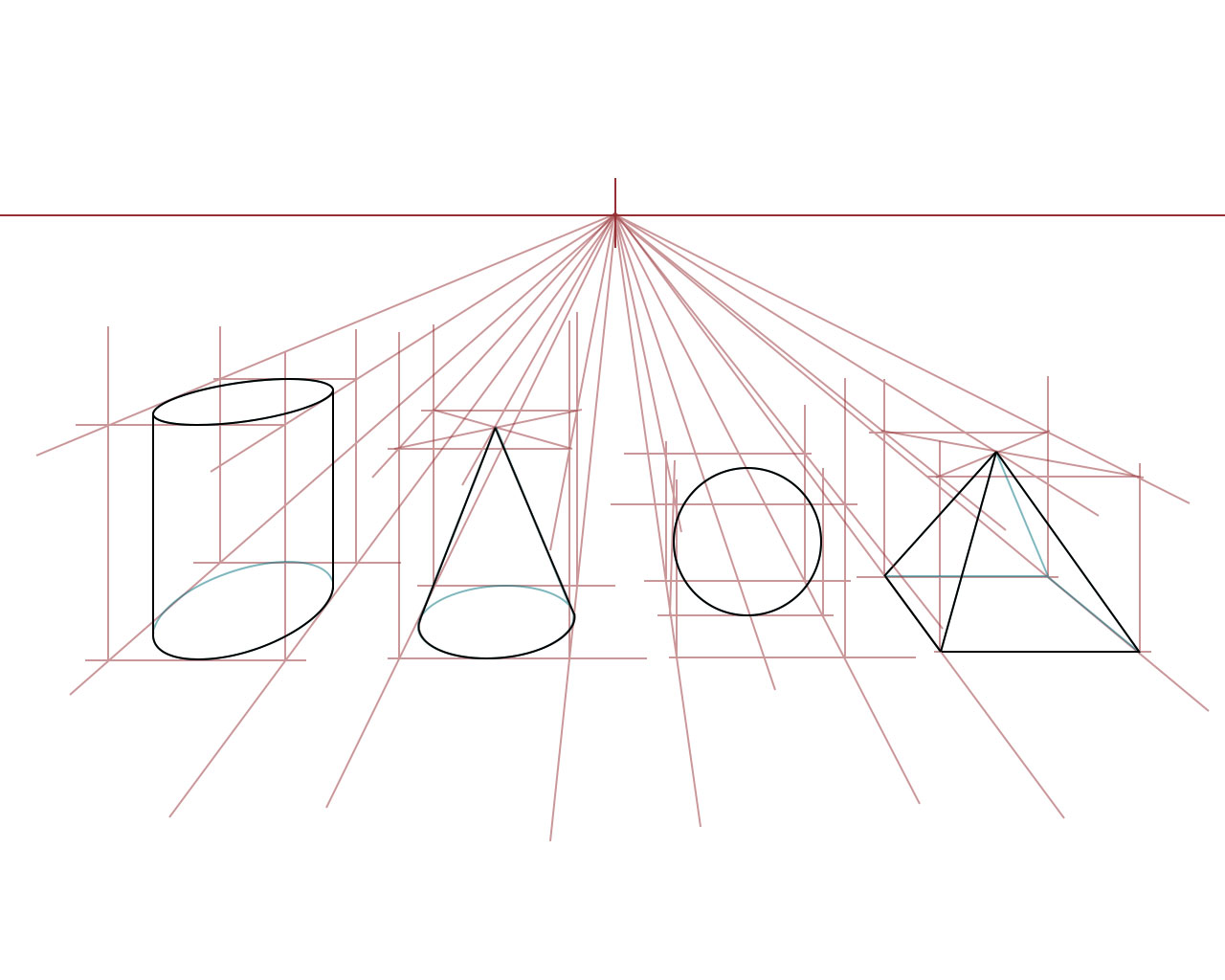 Ш.
Ш.Задание 4
«Лежащий» цилиндр»
Задание более сложное, чем предыдущие, поэтому рекомендуется учитывать состояние пациента. При необходимости можно выделить отдельный учебный день после темы «Простейшие бытовые предметы». Занятие заполнить не только прорисовкой «лежащего» цилиндра, но и построением бытового предмета подобной формы (баллончик из-под краски, бутылка) для закрепления полученных навыков.
Материалы: писчая бумага А-4, простые карандаши, ластик, угольники, линейка.
Этапы
1. Нарисовать произвольно повернутый параллелепипед, основанием которого является квадрат.
2. Разбить основания осями, причем вертикальные будут чуть смещены к дальним ребрам по законам перспективного построения. Выделить точки пересечения осей с ребрами.
Выделить точки пересечения осей с ребрами.
3. Пользуясь полученными точками, построить «неправильные» эллипсы.
4. В основаниях провести диагонали от дальнего верхнего угла к ближнему нижнему. Отметить точки пересечения с эллипсами.
5. Пользуясь полученными точками, построить «неправильные» эллипсы.
6. Самостоятельно нарисовать несколько цилиндров (от двух до четырех, в зависимости от того, как будут получаться). Обсудить, при необходимости исправить (желательно по мере выполнения каждого рисунка).
Рисунок М.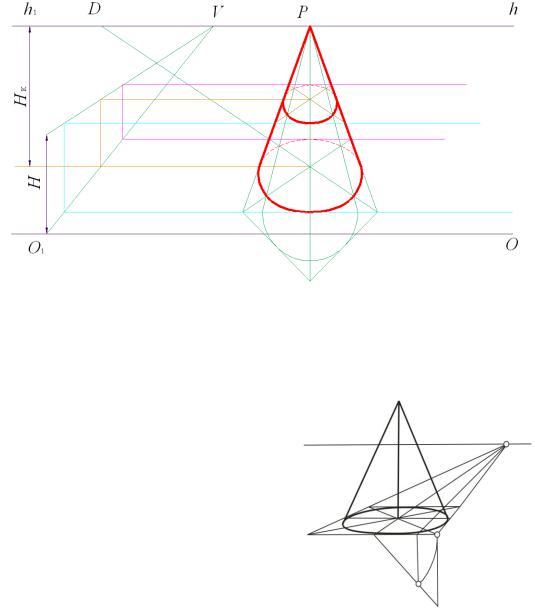 А. А. | ||
Задание 5
«Отрицательный» цвет в геометрическом теле»
Проявить «отрицательный» цвет в геометрическом теле (создать негативно заряженный образ в рамках простейшего геометрического тела). Задание дается для того, чтобы снять умственное напряжение, расслабить и эмоционально взбодрить ученика. Кроме того, оно служит для совершенствования полученных ранее знаний.
Материалы: писчая бумага А-4, шариковая ручка, простые карандаши, ластик, угольники, линейка, акварельная бумага (ватман), акварель, кисти, баночки для воды, тряпочка.
Этапы
1. Продемонстрировать выполненные ранее ученические работы на эту тему.
ПРИМЕР 1Рисунок Ж.О.
. «Я очень не люблю жаб. А у них на коже такие противные влажные бугры. Поэтому я и нарисовала слезящийся конус-выступ мерзкого зелено-бурмалинового цвета». Цель достигнута и вполне элегантно.
Поэтому я и нарисовала слезящийся конус-выступ мерзкого зелено-бурмалинового цвета». Цель достигнута и вполне элегантно.
Рисунок Г.Е.
(фломастеры по акварели)
. На вопрос: «Что это?», пациент ответил: «Да это просто гроб!» Без особых затей, но задача решена.
2. Предложить ученику придумать легенду, включающую какое-либо геометрическое тело, но не рассказывать ее.
3. Нарисовать на листе ватмана формата А-4 соответствующее геометрическое тело, учитывая правила размещения единичного предмета на листе. Преподавателю следует проверить правильность рисунка.
4. Подать его акварелью выбранных тонов.
5. Рассказать (после обсуждения записать) объяснение-эссе. Обсудить работу.
Домашнее задание
1.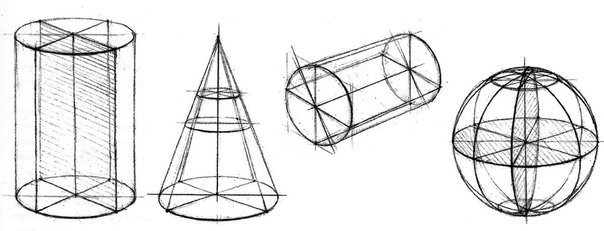 Нарисовать проработанные на занятиях геометрические тела (куб, параллелепипед, конус, цилиндр) на листах писчей бумаги формата А-4 в количестве не менее трех предметов каждого вида. Предметы должны быть разного размера,
прозрачны, построены и выявлены при сохраненных линиях построения.
Нарисовать проработанные на занятиях геометрические тела (куб, параллелепипед, конус, цилиндр) на листах писчей бумаги формата А-4 в количестве не менее трех предметов каждого вида. Предметы должны быть разного размера,
прозрачны, построены и выявлены при сохраненных линиях построения.
2. Построить геометрические тела: шар, призма, усеченный конус, предварительно самостоятельно продумав этапы и элементы построения. Предметы должны быть разного размера, прозрачны, построены и выявлены при сохраненных линиях построения. Работа выполняется на листах писчей бумаги формата А-4 в количестве не менее трех предметов каждого вида.
3. Поработать с отрицательными эмоциями.1). Выбрать наиболее актуальную на данный момент и отобразить ее красками в любой технике, стараясь вложить весь мыслимый и немыслимый негатив.
2). Не торопясь разорвать раскрашенный лист на мелкие кусочки.
Не торопясь разорвать раскрашенный лист на мелкие кусочки.
3). На чистом листе выложить из этих фрагментов «убегающего ежика». Недостающие элементы можно просто дорисовать в любом материале.
4). Придумать и записать историю о получившемся ежике.
Практическая работа № 2. Рисунок цилиндра и конуса в проекции
Практическая работа № 2. Рисунок цилиндра и конуса в перспективеЗадание № 1. Линейно-конструктивное построение геометрического тела — цилиндр. С частичной тоновой проработкой;
Задание № 2. Линейно-конструктивное построение геометрического тела — конус. С частичной тоновой проработкой.
Материал: простой карандаш различной твердости, акварельная бумага, ластик
Порядок выполнения:
Цилиндр — геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности.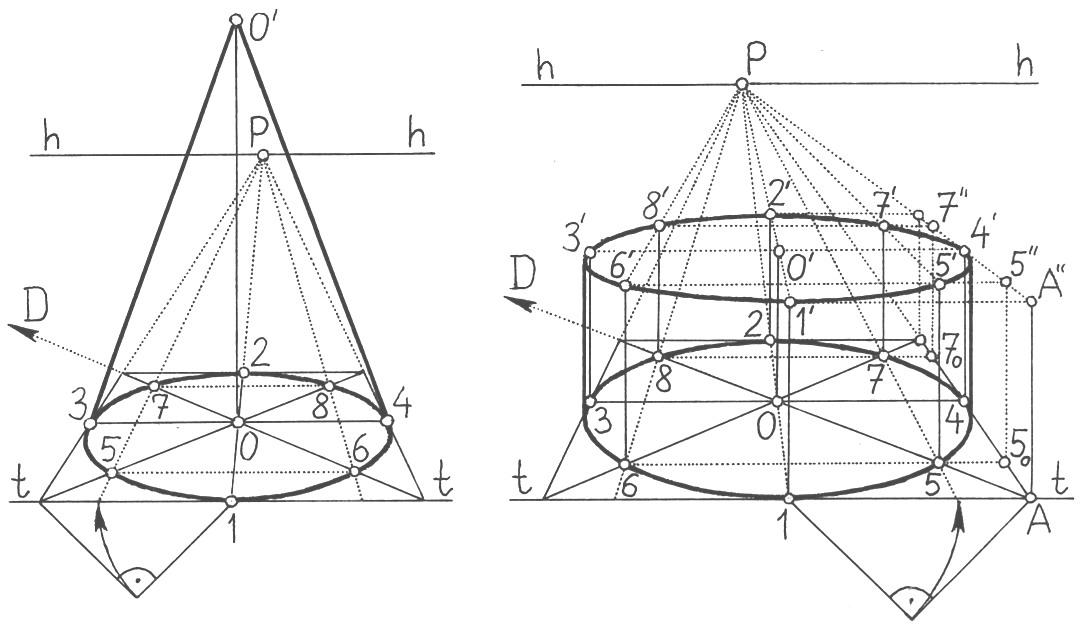 Форма цилиндра своеобразная. В отличие от куба свет по цилиндрической поверхности распределяется во многом сложнее. Основаниями цилиндра служат круглые плоскости, и если они находятся под каким-либо углом (в ракурсе), то выглядят уже эллипсами.
Форма цилиндра своеобразная. В отличие от куба свет по цилиндрической поверхности распределяется во многом сложнее. Основаниями цилиндра служат круглые плоскости, и если они находятся под каким-либо углом (в ракурсе), то выглядят уже эллипсами.
Последовательность рисования цилиндра:
Первый этап. Определение размеров цилиндра, основных пропорций (высоты и ширины). Нахождение его расположения на листе. Построение осевых линий. Для этого определяется положение вертикальной оси цилиндра. Перпендикулярно к ней строятся осевые линии верхнего и нижнего оснований цилиндра.
Второй этап. Прорисовка овалов, передающих перспективное сокращение верхнего и нижнего оснований цилиндра. Определение границ света и тени.
Третий этап. Нанесение светотени для выявления объема. Штрихи подчеркивают форму цилиндра. Обобщение и соблюдение верных тональных отношений в процессе завершения работы для достижения законченности рисунка.Построение цилиндра, расположенного вертикально, начните с компоновки общей формы тела.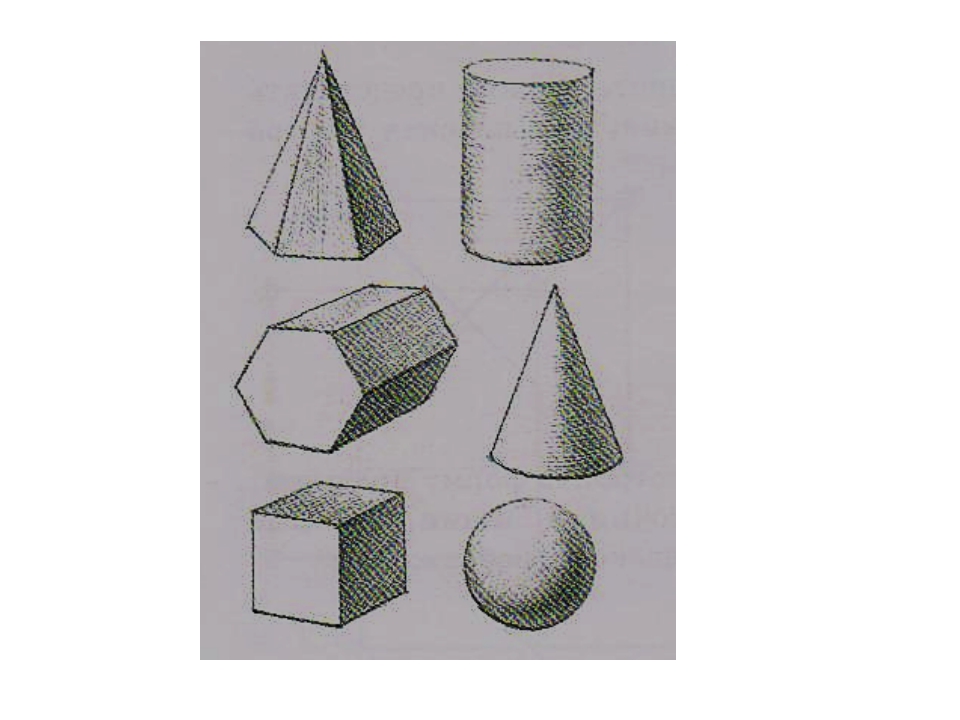 Чтобы не ошибиться в размещении общей формы (белого силуэта) цилиндра в вертикальном формате листа бумаги, проведите легкую вертикаль в середине и зрительно определите высоту изображаемого тела, а затем его ширину.
Чтобы не ошибиться в размещении общей формы (белого силуэта) цилиндра в вертикальном формате листа бумаги, проведите легкую вертикаль в середине и зрительно определите высоту изображаемого тела, а затем его ширину.
Далее построение формы цилиндра оказывается действенным средством развития знаний и практических навыков в рисовании, так как помогает хорошо усвоить правила перспективы и конструктивного строения предметов. Выполняя данную работу, вы должны действовать уверенно, свободно держать карандаш.
Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.

Изображение цилиндра следует начинать с определения основных пропорциональных величин — диаметра оснований и высоты.
Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей — вписыванием в квадрат.
Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра.
Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней.
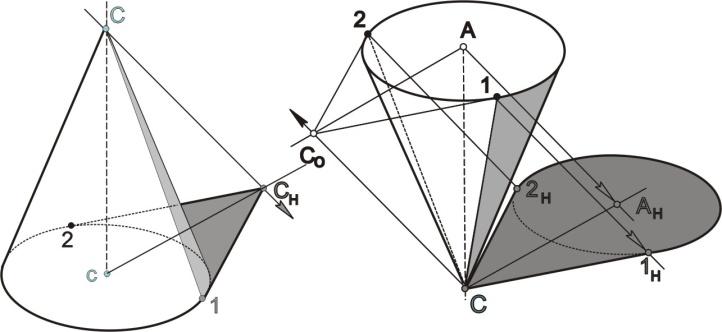
При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.
Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра — ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.
По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.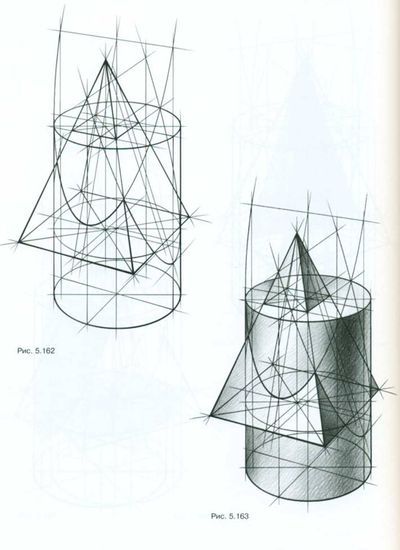
Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.
Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра. Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей.
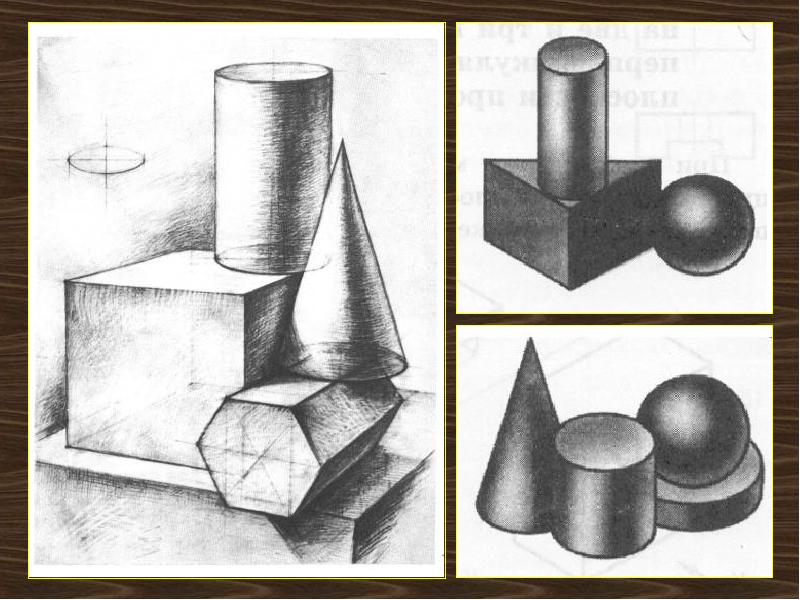 В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.
В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении. Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем — цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол между осью призмы и отрезком линии, которая и будет большой осью эллипса. Эта важная деталь, о ней следует всегда помнить студентам, является причиной грубых ошибок при изображении цилиндра в горизонтальном положении.
 При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.
При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.| Последовательность рисования цилиндра в горизонтальном положении |
Следует обратить внимание, что дальнее основание цилиндра по мере удаления от рисующего всегда несколько шире (по малой оси), чем переднее. Это обусловлено закономерностью перспективы.
Построив таким образом основания и дополнительно уточнив окружности (эллипсы), соединяют их образующими. В завершающей стадии построения изображения следует придать рисунку большую пространственность за счет усиления линий близлежащих и ослабления линий дальних форм.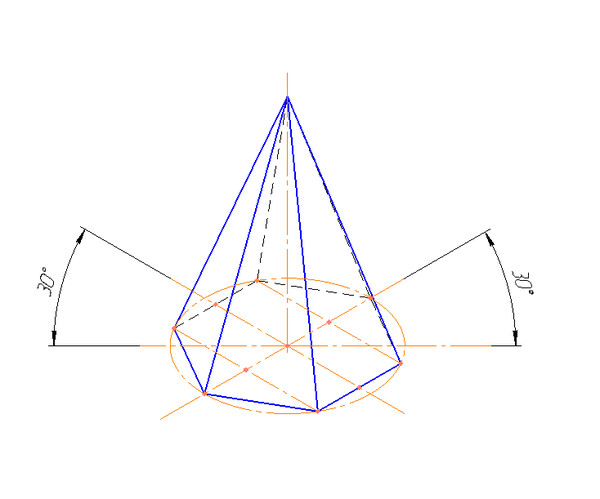
Завершив построение, следует непременно его проверить. Внимательно проверив возможные ошибки, допущенные в процессе построения, и исправив их (если таковые имеются), следует перейти к длительному рисунку с помощью света, тени, полутени и рефлекса.
Принцип освещения очередной модели для рисования с натуры остается прежним. На этот раз вы будете выполнять тоновой рисунок цилиндра — геометрического тела, образованного вращением прямоугольной плоскости вокруг единой оси.
Построив каркас цилиндра, в котором верно изображены в перспективе оба основания (нижнее — немного шире, как это смотрелось в натуре), сравните изображение с натурой и переходите к моделировке формы тоном. Если в тоновом рисунке куба была определенная сложность, вызванная передачей пропорциональных натур светотеневых отношений, то в тональной характеристике цилиндра нужны дополнительные усилия, чтобы понять степень распределения градаций света и тени по его специфической поверхности.
Обязательно разберитесь в градациях, так как вместо передачи объемной формы нарисованное изображение может выглядеть словно помятым или сплющенным.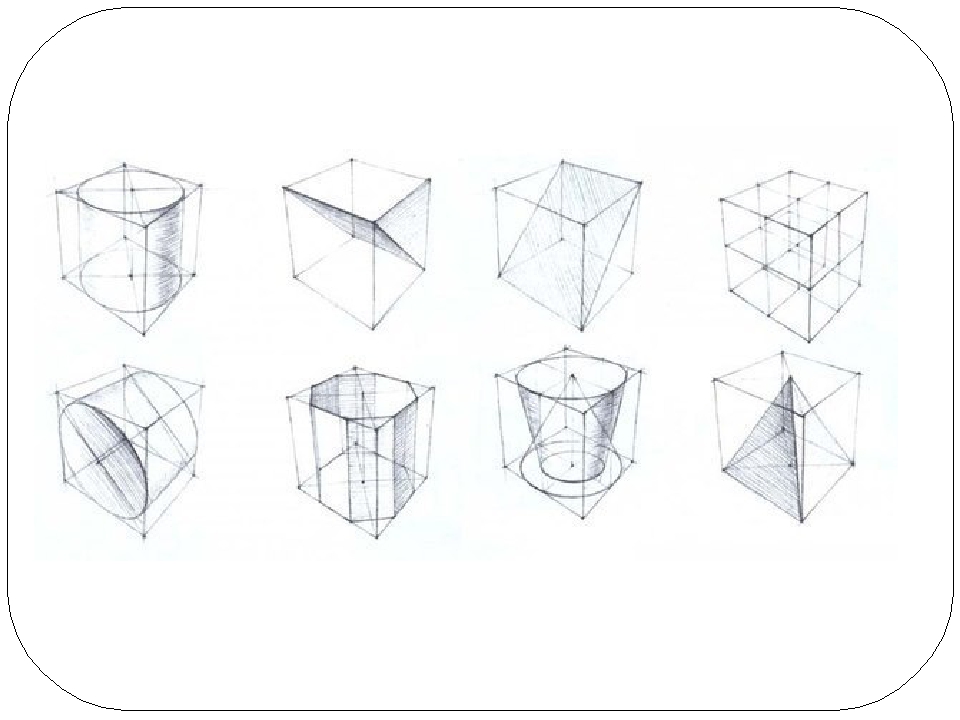 Чтобы этого не произошло, будьте предельно внимательны в моделировке поверхности построенного на бумаге цилиндра.
Чтобы этого не произошло, будьте предельно внимательны в моделировке поверхности построенного на бумаге цилиндра.
Светотеневое решение формы цилиндра подчиняется знаниям рисующего. Каждый видит, как распространяющийся по округлой поверхности цилиндра свет четко строит форму геометрического тела. Наиболее ярко выглядит на цилиндрической поверхности небольшой участок. Это блик, и его явление вызвано тем, что на эту часть объема световые лучи попадают строго перпендикулярно. Далее свет начинает, как бы скользить по закругляющейся поверхности и, разумеется, ослабляет освещенность предмета, пока его воздействие не прерывается заходящей за границу между ним и тенью областью, становящейся самым темным пятном. Следовательно, цилиндрическая поверхность дает четкое зрительное представление последовательного распределения светотеневых градаций примерно в таком чередовании: полутон, свет, блик, свет, полутон, тень, рефлекс. Конечно, переходы между ними совершенно не различимы, и это одна из сложностей передачи в рисунке объемной формы цилиндра.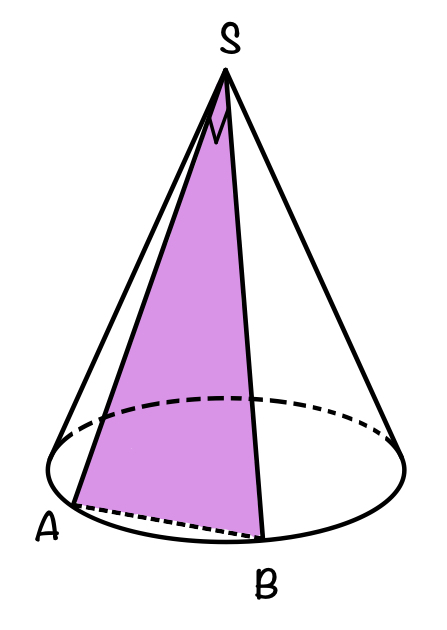 Значит, вам необходимо не добиваться абсолютного сходства нарисованного цилиндра с натурой, а следить за верной передачей пропорциональных ей отношений градаций тона.
Значит, вам необходимо не добиваться абсолютного сходства нарисованного цилиндра с натурой, а следить за верной передачей пропорциональных ей отношений градаций тона.
Фон в тоновом рисунке служит неотъемлемой частью
пространственного изображения. Кроме того, он влияет на общее состояние освещенности, оказываясь то нейтральным, то активно воздействующим на восприятие предмета.
Последовательность изображения вертикальностоящего цилиндра, расположенного ниже горизонта
Последовательность изображения горизонтального цилиндра,
расположенного ниже горизонтаОпределение тени
Рисование конуса
Конус определяется радиусом окружности основания и точкой вершины, поэтому при его построении, так же, как и при построении конструкции цилиндра, работу следует начинать с построения окружностей оснований в перспективном ракурсе.
Построив окружность (эллипс) основания конуса, необходимо определить его вершину.
 Для чего от центра основания эллипса проводят вверх вертикальную линию — ось вращения, перпендикулярную к большой оси эллипса. Следует напомнить, что ось вращения и есть ось конуса, которая, независимо от положения в пространстве относительно угла зрения рисующего, всегда перпендикулярна к кругу основания конуса. Определив ось конуса с учетом его пропорции, отмечают точкой его вершину. После этого на окружности основания симметрично намечают пространственные точки образующей и соединяют их с точкой вершины конуса.
Для чего от центра основания эллипса проводят вверх вертикальную линию — ось вращения, перпендикулярную к большой оси эллипса. Следует напомнить, что ось вращения и есть ось конуса, которая, независимо от положения в пространстве относительно угла зрения рисующего, всегда перпендикулярна к кругу основания конуса. Определив ось конуса с учетом его пропорции, отмечают точкой его вершину. После этого на окружности основания симметрично намечают пространственные точки образующей и соединяют их с точкой вершины конуса.При изображении конуса в горизонтальном положении, независимо от угла поворота и ракурсов, следует исходить из того, что поверхность круга основания конуса всегда должна быть перпендикулярна оси вращения. Поэтому большую ось эллипса, вписанного в квадрат основания конуса, необходимо строить на линиях, проведенных под прямым углом к оси конуса. Касаясь построения усеченного конуса, нужно отметить, что он, как и цилиндр, определяется нижним и верхним основаниями и их взаимным расположением, лишь с той разницей, что диаметры этих оснований различны, а большие оси эллипса по отношению к оси конуса располагаются по-прежнему под прямым углом, за исключением случаев, когда секущая плоскость проходит под другими углами.
:max_bytes(150000):strip_icc()/2pt3dpyramid4-56a26cd13df78cf77275809b.jpg)
1. Рисунок цилиндра с тональным решением ,
2. Рисунок конуса с тональным решением
Зрение — Перспектива. Все о перспективе.
Страница 6 из 17. Список главЗрение
Расстоянием наилучшего зрения называется расстояние, при котором человек с нормальным зрением свободно читает книгу, отчетливо видит детали предмета. Это расстояние обычно равно 25-30 см. Углом зрения называется угол, под которым человек может видеть предметы, причем предполагается неподвижность головы и глаза. Углом наилучшего зрения в этом случае называется угол, при котором предмет ясно виден, а именно угол, равный примерно 23 градуса.
Так как размеры картины К (на рисунке слева) всегда несколько больше изображаемого на ней предмета, угол зрения для картины принимается равным 28 градусов (нормальный угол зрения), откуда следует, что наибольший размер картины L (ширина или высота) должен быть вдвое меньше главного расстояния D, т. е. расстояния точки зрения С до картины: D=2L. Следовательно, чем больше картина (предмет), тем дальше должна быть расположена точка зрения. Ориентировочно расстояние D принимается равным от полутора до двух диагоналей картины.
е. расстояния точки зрения С до картины: D=2L. Следовательно, чем больше картина (предмет), тем дальше должна быть расположена точка зрения. Ориентировочно расстояние D принимается равным от полутора до двух диагоналей картины.
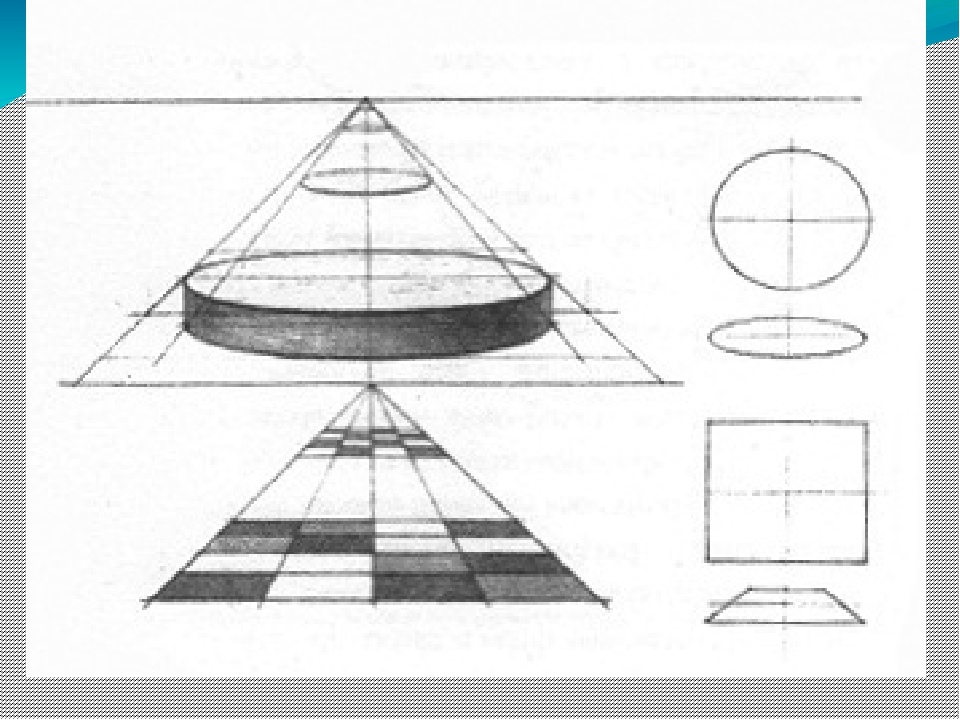
Направленные в точку зрения парные лучи, представляющие собой углы зрения, образуют круговой конус — конус видимости (на рисунке справа), который, пересекаясь с картиной, образует круг, называемый полем зрения. В действительности этот конус несколько неправильной формы, так как пределы движения глаз человека в разные стороны не одинаковы.
Полный угол зрения обоими глазами в вертикальной плоскости достигает 125 градусов, а в горизонтальной 176.
Чем больше угол зрения, принятый при построении перспективы, тем края изображения больше искажаются, кажутся уродливыми и неестественными, а поэтому считается, что на картине могут изображаться лишь те предметы, которые находятся внутри конуса с углом при вершине не более 28-30 градусов, т.е. угол зрения не должен превышать этой нормы.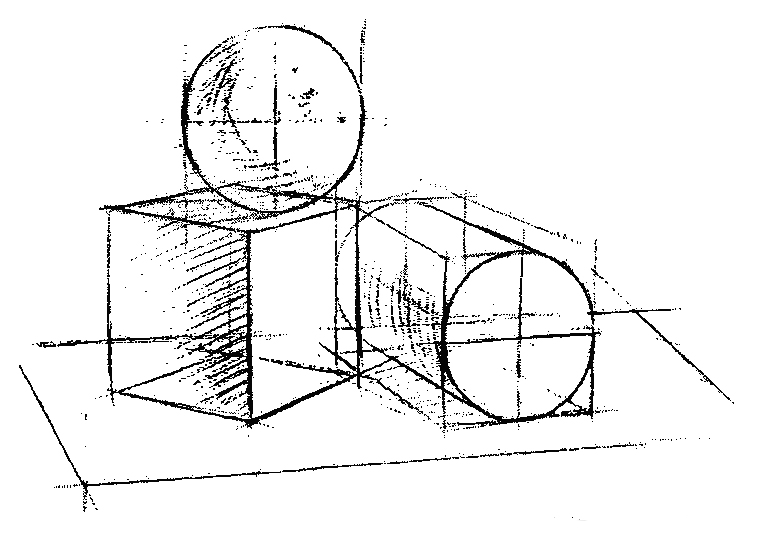 Более редко применяется угол 30-37 градусов и в исключительных случаях 45-50 градусов.
Более редко применяется угол 30-37 градусов и в исключительных случаях 45-50 градусов.
- Глава 5: «Отступления от правил»
- Глава 7: «Линия схода»
Тэг:
ПОЛЕ ЗРЕНИЯ — перспектива — LiveJournal
Наш глаз видит предметы, которые можно охватить взглядом по горизонтали в пределах угла зрения, не превышающего 53°. Все видимые точки предметов соединены с глазом так называемыми лучами зрения. Главный луч находится в центреугла зрения и делит его пополам. Если на картине построить перспективу так, что главный, или центральный, луч зрения будет находиться с краю листа бумаги, то зритель мысленно продолжит картину и за ее пределами, так как угол зрения от главного луча одинаковый и справа и слева. Исходя из этого, главный луч зрения не следует брать близко к боковым сторонам картины. Мы видим только те предметы, в сторону которых обращен наш взор, а видимость ограничена так называемым полем зрения. На близком расстоянии мы можем увидеть целиком только небольшие предметы, а крупные лишь частично уместятся в поле зрения. Яснее всего видны предметы в центральной части поля зрения. |
Построение окружностей и тел вращения в перспективе
1. Лекция 6. Построение окружностей и тел вращения в перспективе
1. Построение окружностей ввертикальных плоскостях
2. Построение горизонтальных
окружностей
3. Построение горизонтальных
окружностей с центром на оси Р
4. Рациональные способы построения
горизонтальных окружностей
2. Построение окружностей в вертикальных плоскостях
AB
A
B
F1
3. Построение полуокружности в вертикальной плоскости
k2h3
A
Построение
полуокружности
в вертикальной
плоскости
1
k1
В
k
h2
2
h С
A
1
k
4. Построение полуокружности в вертикальной плоскости
5. Построение толщины арки
в F2в F1
в F2
в F1
F1
P
F2
S
Построение толщины арки
6.
 Построение толщины арки в F2
Построение толщины арки в F2в F1
в F2
в F1
7. Построение толщины арки
в F2в F1
в F2
в F1
8. Построение горизонтальных окружностей: 1. построение перспективы квадрата, описанного вокруг окружности; 2. построение
F1K
Построение горизонтальных
окружностей:
1. построение перспективы квадрата,
описанного вокруг окружности;
2. построение окружности по 8-ми точкам
F1
3
4
2
1
9. Построение горизонтальных окружностей
в F2в F1
7
3
6
4
8
2
5
1
А
10. Построение горизонтальной окружности по 8 точкам
в F2в F1
11. Построение горизонтальных окружностей с центром на оси Р Использование Fд – дистанционной точки схода Fд – диагональная или
Построение горизонтальных окружностей с центром на оси РИспользование Fд – дистанционной точки схода
FД — точка схода для диагоналей квадрата,
у которого две стороны
картине, а две
FД
ей
SP=PFД
Fд – диагональная
или дистанционная
точка схода
FД
S
12.
 1. по вертикали Р откладывается НВ, на которой размещена горизонтальная окружность 2. на уровне НВ горизонтально откладывается Построение горизонтальных окружностей с
1. по вертикали Р откладывается НВ, на которой размещена горизонтальная окружность 2. на уровне НВ горизонтально откладывается Построение горизонтальных окружностей сцентром на оси Р:
O1
1. по вертикали Р откладывается
НВ, на которой размещена
горизонтальная окружность
2. на уровне НВ горизонтально
откладывается НВ диаметра
окружности
3. точка Р соединяется с концами
горизонтального диаметра
4. из центра окружности проводится
диагональ в точку схода Fд
h2 — h3
FД
13. Построение горизонтальных окружностей с центром на оси Р
А1
5
8
2
4
7
6
3
Построение
горизонтальных
окружностей с
центром на оси Р
14. Построение горизонтальных окружностей с центром на оси Р
А1
8
5
Rнат
4
6
2
7
3
Построение
горизонтальных
окружностей с
центром на оси Р
15. Построение горизонтальных окружностей одного диаметра, расположенных на разной высоте
O1Построение
горизонтальных
окружностей одного
диаметра, расположенных
на разной высоте
h2 — h3
FД
16.
 Рациональные способы построения горизонтальных окружностей одинакового диаметра Нат.R
Рациональные способы построения горизонтальных окружностей одинакового диаметра Нат.RНат. выс. расположения
окр. О 2 над линией горизон та
1
Нат.R
О2
2
О2
17. Рациональные способы построения горизонтальных окружностей одного диаметра
57
8
5
7
6
3
О2
О2
8
Нат. выс. расположения
окр. О2 над линией горизонта
6
4
О2
18. Построение соответственных точек
12
О2
Fx
О2
Fk
19. Построение горизонтальных окружностей, лежащих на поверхности конуса
О2S
S
20. Построение горизонтальных окружностей, лежащих на поверхности конуса
О2S
О2
S
Построение горизонтальных
окружностей, лежащих на
поверхности конуса
21. Построение горизонтальных окружностей, лежащих на поверхности конуса
О2S
О2
S
Построение горизонтальных
окружностей, лежащих на
поверхности конуса
22.
 Построение горизонтальных окружностей, лежащих на поверхности конуса 1
Построение горизонтальных окружностей, лежащих на поверхности конуса 12
1
О2
2
S
Построение
горизонтальных
окружностей,
лежащих на
поверхности конуса
Перспектива геометрических тел — Энциклопедия по машиностроению XXL
Глава XIV. ПЕРСПЕКТИВА ГЕОМЕТРИЧЕСКИХ ТЕЛ [c.111]Глава 18 ПЕРСПЕКТИВА ГЕОМЕТРИЧЕСКИХ ТЕЛ 66. ПЕРСПЕКТИВА ГРАННЫХ И КРУГЛЫХ ТЕЛ [c.246]
Контрольные вопросы. 1. С помощью каких элементов картины можно построить перспективу геометрических тел 2. Как строится перспектива куба, если одна из заданных его сторон расположена параллельно картине На картине даны точки Р и Д/2. 3. Объяснить построение перспективы параллелепипеда, стоящего на предметной плоскости под произвольным углом к картине, при условии, что на картине задана одна из его сторон и даны точки Р и 0/2. 4. С чего начинают построение прямого кругового цилиндра, стоящего на предметной плоскости, если известны размеры диаметра основания и высоты цилиндра
[c.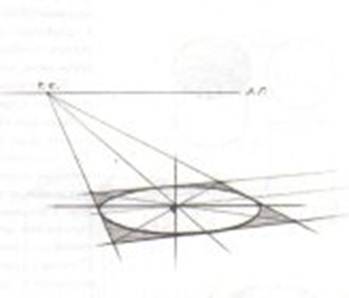 252]
252]
На черт. 358 даны ортогональные проекции двух геометрических тел, план которых тождествен ранее рассмотренной фигуре. Не повторяя объяснений, относящихся к построению вторичной проекции, опишем процесс создания перспективы предмета. [c.167]
Построить методом архитекторов перспективу группы геометрических тел при заданной линии горизонта (черт. 386). [c.179]
Рисование экстерьера или интерьера, как и рисование группы геометрических тел, строительных деталей или строительных узлов, начинают с разметки расположения отдельных элементов, изображения натуры на листе бумаги и определения положения линии горизонта и точек схода. Затем переходят к прорисовке контура всех входящих в экстерьер или интерьер объектов с учетом закона перспективы. [c.181]
Для построения перспективы отдельных геометрических тел, а также группы тел по заданным размерам необходимо пользоваться перспективными масштабами. [c.111]
Построить перспективу группы геометрических тел по их прямоугольным проекциям. [c.112]
Умение строить перспективы простейших геометрических тел таких, как куб, параллелепипед, призма, пирамида, конус, цилиндр, тор в значительной мере способствует реалистической передаче на картине окружающего предметного мира. [c.246]
Учитывая постепенность и индивидуальность развития пространственного мышления учащихся, следует больше выполнять упражнений с моделями (геометрическими телами, деталями несложной формы). Научившись понимать построение проекций геометрических тел и простых по форме деталей, можно в качестве упражнения задавать на поверхностях этих тел отдельные точки, отрезки и строить проекции этих точек и отрезков на всех видах. Весьма полезно делать упражнения на определение положения точки на аксонометрическом изображении геометрического тела (предмета) по заданному комплексному чертежу этого предмета, на котором задается искомая точка. Примеры построения подобных задач изложены в учебнике, а упражнения в достаточном количестве приведены в задачнике (см. Задачник по черчению и перспективе, 19), [c.312]
Из существующих типов фрикционных вариаторов с жесткими телами качения основные перспективы применения имеют а) для малых мощностей— шаровые вариаторы с регулированием скорости наклоном геометрических осей врашения шаров б) для средних мощностей — торовые вариаторы с регулированием скорости наклоном роликов (по схеме ЦНИИТМАШ конструкции завода. Красный пролетарий ). [c.443]
Мы ограничимся сказанным в отношении той части теории теней, которая имеет целью геометрическое определение их контуров нам остается рассмотреть ее другую часть, относящуюся к определению интенсивности оттенков, придаваемых различными частями затененных поверхностей, для лучшего изображения на рисунках света и тени, являемой данными предметами в действительности. Чтобы охватить подобный вопрос во всем его объеме, уже недостаточно ограничиться рассмотрением, как мы это делали до сих пор, светящегося тела, тела непрозрачного, и поверхности, на которую падает тень, но также нельзя не принимать во внимание различные дополнительные обстоятельства мы должны рассматривать предметы вместе со всем, что их окружает в действительности, и учитывать, помимо прочих вещей, также и положение наблюдателя и изменения, которые может испытать свет на пути к его глазу, — только тогда мы можем передать все ощущение картины, на которую направлен его взгляд. Эти соображения требуют, чтобы мы предпосылали тому, что хотим сказать по этому вопросу, изложение теории перспективы. [c.210]
Нужно также знать закономерности изображения в перспективе некоторых геометрических тел, которые являются основой изображаемых на рисунках пространственных форм (зданий, интерьеров, предметрв и т. п.). К таким телам следует отнести куб, прямоугольный параллелепипед, цилиндр, конус, шар. [c.204]
Большая ось — чертеж в перспективе
Это верно независимо от угла или положения эллипса.
Так что не делайте ошибки, рисуя квадрат в ракурсе и используя его центр для определения главной оси эллипса. В результате фигура будет выглядеть примерно так (справа).
Кроме того, если вы хотите нарисовать полукруг (или цилиндр), вы не можете нарисовать эллипс и рассматривать любую сторону большой оси как половину передней; укороченный круг. Например, цифра слева не половина, а меньше.
Однако две справа являются половинками, потому что диаметр круга используется в качестве разделительной линии.
Этот поразительный факт часто вызывает большие затруднения (даже в книгах по этой теме). Какая связь между центром круга и осями эллипса?
Цилиндры
Независимо от положения или угла эллипса, его большая и малая оси всегда оказываются под прямым углом.
ПРИ ЧЕРТОВАНИИ ЦИЛИНДРА — ЕГО ЦЕНТРАЛЬНАЯ ЛИНИЯ ВСЕГДА ДОЛЖНА БЫТЬ ПРОДОЛЖЕНИЕ МЛАДШЕЙ ОСИ СВЯЗАННОГО ЭЛЛИПСА.Следовательно, эта центральная линия (ось колес, перекладина грифов, вал гироскопа и т. Д.) Всегда оказывается под прямым углом к главной оси связанного с ней эллипса.
Но обратите внимание, что эта центральная линия соединяется с эллипсом в центральной точке круга, а не с центром эллипса. (В противном случае вал был бы эксцентричным — буквально «не по центру». См. Предыдущую страницу.)
Перерисовывая два объекта выше, мы видим, что квадраты с укороченным ракурсом в любом направлении могут быть построены как направляющие по кругу.Но в любом случае ПРОТИВОПОЛОЖНЫЕ ТОЧКИ ЗАЖИГАНИЯ (точки) ЗАКОНЧИВАЮТ ЛИНИИ ДИАМЕТРА ЧЕРЕЗ ЦЕНТР КРУГА. (На самом деле эти линии расположены под прямым углом.)
Большая ось эллипса (пунктирная) не имеет к этому никакого отношения — это просто направляющая линия для рисования эллипса. (Заметим еще раз, что центр эллипса ближе к наблюдателю, чем центр круга.)
Ниже приведены некоторые примеры применения этих принципов.
У конуса внутри цилиндра (справа), естественно, центральная линия параллельна столешнице.Следовательно, вершина конуса находится в воздухе. Чтобы нарисовать конус, лежащий на столе, его вершина должна опускаться (стрелки) так, чтобы его центральная линия приходилась примерно на пунктирную линию.
Конус справа нарисован с опущенной центральной линией. (Это движение немного сокращает длину и делает эллипс более округлым.)
ПОЭТОМУ, КОНУСЫ, РАСПОЛОЖЕННЫЕ НА СВОИХ СТОРОНАХ, ИМЕЮТ ЦЕНТРАЛЬНЫЕ ЛИНИИ, НАКЛОНЕННЫЕ К ПЛОЩАДКАМ, НА КОТОРЫХ ОНИ ОСТАВЛЯЮТСЯ.
Сходство эллипсов справа указывает на то, что эти конусы ориентированы одинаково, но разной длины.
Хотя здесь разные эллипсы и укороченная длина предполагают, что конусы направлены в разные стороны и примерно одинаковы. (Обратите внимание, что стороны конуса всегда соединяются с эллипсом по касательной.)
Рисование конусов аналогично рисованию цилиндров. Центральная линия конуса также является продолжением малой оси соответствующего эллипса … она лежит под прямым углом к большой оси эллипса. . . и он соединяется с эллипсом не в центральной точке эллипса, а за ним.Изучите эти различные принципы на рисунках выше.
Рисование конусов аналогично рисованию цилиндров. Центральная линия конуса также является продолжением малой оси соответствующего эллипса … она лежит под прямым углом к большой оси эллипса. . . и он соединяется с эллипсом не в центральной точке эллипса, а за ним. Изучите эти различные принципы на рисунках выше.
- Круги, эллипсы, конусы, цилиндры и сферы, нанесенные на рисунок «космической эры».
Глава 14: ТЕНЬ И ТЕНЬ
Во-первых, давайте проясним наши термины: SHADE существует, когда поверхность отворачивается от источника света. ТЕНЬ существует, когда поверхность обращена к источнику света, но не может получить свет из-за какого-то промежуточного объекта.
Например: этот подвесной куб имеет несколько поверхностей на свету и несколько в тени (те, которые отвернуты от света). Столешница повернута к свету и будет полностью «в свете», за исключением тени, «отбрасываемой» на нее кубом выше.Можно сказать, что затененная поверхность промежуточного объекта «отбрасывает» тень на освещенную поверхность.
ЛИНИЯ ТЕНИ — это линия, которая отделяет те части объекта, которые находятся «в тени», от тех, которые находятся «в свете». Другими словами, это граница между тенью и светом. Эта линия тени важна, потому что она, по сути, отбрасывает, формирует и определяет тень. (Справа)
Обратите внимание, что линия тени плоского двухмерного объекта является его непрерывной линией края.(Одна сторона объекта освещена, другая — в тени.)
Тень и тень естественным образом существуют только при свете. Обычно свет бывает двух типов, в зависимости от его источника. Один тип создает узор из параллельных световых лучей, другой — радиальный узор.
- Солнце, конечно, излучает свет во всех направлениях, но лучи, достигающие Земли, находящиеся на расстоянии 93 миллионов миль от источника, по сути, представляют собой небольшую горстку одиночных лучей, фактически параллельных друг другу.
Другой тип света исходит от местного точечного источника, такого как лампочка или свеча. Здесь близость источника света означает, что объекты получают световые лучи, которые излучаются наружу из одной точки. Поэтому при рисовании локальными точечными источниками лучи света должны быть радиальными.
Читать здесь: Top Vi
Была ли эта статья полезной?
Построение конуса в сложном виде: learnart
Предыдущие уроки по этой теме в конце.
Так как же на практике конструировать вещи в перспективе, используя все, что мы узнали? Например, я хочу нарисовать конус. Конус — это трехмерный объект вращения прямоугольного треугольника — повернувшись вокруг прямоугольного треугольника, вы получите конус. Во-первых, я хочу построить его в простой фронтальной позиции:
Нарисуйте линию ширины (центральная ось круглой основы).
Поместите точку на горизонте прямо над его центром: в фронтальном положении конус всегда изображается так, как если бы основная точка находилась прямо на его центральной вертикали.
Проведите две линии глубины.
Постройте квадрат — проведите линии от точек D через центр конуса, разрезая линии глубины так, чтобы их сечения равнялись половине ширины линии.
Нарисуйте эллипс.
Соедините концы секции ширины линии с точкой на вертикали центра конуса.
Я хочу поставить конус на бок. Что мне делать?
Во-первых, мне нужно знать, какой угол он будет образовывать с горизонтальной плоскостью.Но я не использую транспортир, и никто не хочет пользоваться даже линейкой. Мы хотим измерять вещи на глаз. Максимум, на что мы способны, — это нарисовать приблизительно 90 ° или ∠45 °. Итак, представьте, что образующая (боковая линия) конуса горизонтальна, нарисуйте перпендикулярную линию и разделите ее на отдельные единицы, как показано на рисунке выше. С этим методом нам не нужен транспортир или линейка.
Также опустите перпендикуляр с одного из концов базовой оси, нам также нужно, чтобы он пересекал образующую.
Вот как выглядит этот конус, поставленный на бок.Как видите, базовая плоскость не видна, потому что основная точка находится слева. Также он может быть построен без линейки, чего мы и хотим.
Теперь я хочу повернуть этот конус на 45 °, сдвинув его кончик.
Постройте квадрат со сторонами, равными образующей конуса.
Контур круга с радиусом, равным стороне этого квадрата, разрезает его диагональ на части с соотношением 1: 3.
Перпендикуляр, падающий из верхней точки основания, по-прежнему разрезает образующую конуса с соотношением 1: 6.
Горизонтальная ось основания конуса направлена в точку D, так как ее угол составляет 45 °. Основание представляет собой нормальный эллипс, поэтому его можно вписать в квадрат.
Предыдущие руководства по перспективе:
Getting started from learnart
https://www.reddit.com/r/ learnart / comments / f0nlmh / depth_lines_constructing_a_cube_in_detail /
https: //www.reddit.com / r / learnart / comments / f1eg1p / trigonometry_but_you_are_an_artist /
Horizontal lines. Constructing a right angle. from learnart
900psit www. r / learnart / comments / f56nep / lines_of_special_and_general_positions /
Серия уроков по рисованию в линейной перспективе [2 из 6] — Точки схода, линия горизонта, конус видения и другие объяснения элементов перспективы
Здравствуйте, и добро пожаловать обратно в модель . второй видеоролик из этой серии уроков о том, как рисовать перспективу.
На случай, если вы пропустили предыдущий урок, не забудьте щелкнуть ссылку ниже, чтобы посмотреть его сейчас:
Урок с перспективой 1 — Введение в рисунок в перспективе
Итак, в сегодняшнем уроке мы разберем все основные компоненты перспективного рисунка, чтобы вы могли получить действительно исчерпывающий обзор всей картины и действительно знать, как все сочетается друг с другом.
Итак, вот все элементы перспективного чертежа, о которых вам нужно знать:
(Примечание: ниже приводится краткое изложение определений всех элементов перспективы.Для более подробного объяснения, пожалуйста, обратитесь к видео выше.)
Наблюдатель
Каждый перспективный рисунок или изображение рассматривается с точки зрения наблюдателя. Наблюдатель похож на главного героя, и мы, по сути, видим сцену его глазами.
Конус зрения
Конус зрения определяется как объем того, что наблюдатель может ясно видеть, глядя на сцену.
Конус зрения важен, потому что он определяет то, что будет на нашем перспективном рисунке.
Уровень глаз / линия горизонта
Уровень глаз — это просто высота глаз наблюдателя от земли. Если глаза наблюдателя находятся на высоте 6 футов от земли, то уровень глаз будет на высоте 6 футов.
Уровень глаз также совпадает с линией горизонта на перспективном чертеже.
Некоторым художникам нравится определять линию горизонта как линию, где небо встречается с землей. Это верное и полезное определение для пейзажных рисунков на открытом воздухе, где эта линия четко видна.
Но это определение не подходит для сцен в помещении, где небо и земля закрыты.
Поэтому гораздо лучше помнить, что линия горизонта всегда совпадает с уровнем глаз наблюдателя.
Плоскость изображения
Плоскость изображения может использоваться как сама бумага для рисования. Он принимает все трехмерные изображения сцены и преобразует их в двухмерный рисунок.
Точки исчезновения
Точки исчезновения возникают из-за того, что по мере того, как объекты удаляются от наших глаз, они кажутся меньше.
Следовательно, на перспективном рисунке, когда предметы удаляются от наблюдателя, они становятся все меньше и меньше, пока не покажется, что исчезают (или исчезают) в точке схода.
Точки схода — важный компонент перспективного рисования, потому что они помогают художнику определить, как рисовать все прямые линии на рисунке.
Мы еще поговорим о точках схода в будущих уроках.
Итак, это в основном все элементы перспективного рисунка.Надеюсь, это не запутало.
В завтрашнем видео, , мы собираемся погрузиться в различные типы перспективы, и я объясню, как работает одноточечная перспектива.
Теперь, если вы уже подписаны на мой бесплатный информационный бюллетень по рисованию, все, что вам нужно сделать, это посмотреть в свой почтовый ящик, чтобы получить письмо от меня завтра.
Но если вы еще не зарегистрировались, вы можете сделать это бесплатно, введя свой адрес электронной почты в форму ниже…
Итак, это все для сегодняшнего урока перспектив.
Если вам понравился этот урок, нажмите кнопку «НРАВИТСЯ» на этой странице, а также поделитесь им со всеми своими друзьями с помощью кнопок социальных сетей на этой странице.
Пожалуйста, оставьте комментарий ниже, чтобы сообщить мне, что вы думаете.
Спасибо, что зашли, увидимся завтра!
Вопрос о перспективе: Cone of Vision
Скотт — великий художник, и эта страница о перспективе верна (я могу за это поручиться) и определенно имеет свое собственное применение.Но я рекомендую читать его умеренно, потому что он очень технический, и вам также необходимо разбираться в фотографии (поэтому Скотт также говорит о фотографии). Единственное, что отличает 60- и 90-градусное зрение, — это их соответствующий охват (или, на жаргоне фотографии, поле зрения). Зрение в меньшей степени создает меньшее покрытие, в то время как зрение в большей степени создает большее покрытие. Покрытие — это то, насколько большим физически (это важно, физически, а не визуально) должен быть объект, чтобы поместиться в кадр.Лицо физически маленькое, а небоскребы физически большие. В основном это и есть «короткий объектив» и «длинный объектив», охват (длинный объектив также называется телеобъективом, а короткий объектив также называется широким объективом). Для небольших вещей, таких как портреты, мы использовали бы длинный объектив, в то время как для пейзажей, таких как здания, мы будем использовать короткие линзы. Длинные линзы дают диапазон от 20 до 5 градусов зрения, нормальные линзы (например, 50 мм) дают что-то около 45 градусов (я думаю, Скотт ошибается, называя 50 мм, чтобы иметь 60 градусов зрения), в то время как короткие линзы производят от 60 до 140 градусов. зрение.Теперь вы начинаете понимать, почему, когда мы снимаем портреты, мы использовали бы длинный объектив, потому что тот факт, что он дает небольшой (всего от 20 до 5) градус зрения, соответствует физическому размеру лица на портретах, которое также небольшой. Если вы попытаетесь использовать короткие линзы (от 60 до 140 градусов) для портретов, это то, что также замечает Скотт, вы получите искажение, потому что вы пытаетесь использовать зрение с большим углом для кадрирования небольшого объекта. Лицо будет выглядеть шире, чем должно быть (это то, на что многие стрелки в Instagram жалуются, что их щеки выглядят большими, потому что у нашего телефона обычно короткие линзы).Как я уже упоминал, какими бы увлекательными ни были цифры, от этой информации будет меньше пользы, когда дело доходит до реального рисования.Если вы хотите использовать эту информацию, возьмите зеркалку и начните делать снимки самостоятельно, а затем изучите фотографии своей зеркальной фотокамерой. берет. Таким образом, вы сможете узнать, как работают эти числа, и не только это, а также увидеть, как эти числа влияют на внешний вид объектов, которые вы фотографируете.
Основные трехмерные формы
На трехмерном уровне существует пять основных форм: сфера, конус, цилиндр, тор и куб.Все трехмерные объекты могут быть построены из частей этих пяти форм. Вещи с плоскими поверхностями и резкими изменениями плоскости поверхности, такие как углы дома или шестигранная головка болта, относятся к кубам. Изогнутые плоскости, такие как округлые подлокотники дивана или рябь флага, относятся к конусам или цилиндрам. Неровности, вмятины и холмы относятся к сферам. Барбекю состоит из сфер и цилиндров; почтовый ящик — это полуцилиндр и куб. Закругленный круглый обод чашки относится к тору, который также является основной формой спиральной змеи или звеньев цепи.
Изучая основные формы, вы также должны учитывать, как они проявляются в негативе. Например, кратер — это отрицательная сфера; колея или канавка — отрицательный цилиндр; пустой прямоугольный бассейн — часть отрицательного куба.
Сфера
Сфера — это самая легкая из форм для рисования, потому что независимо от вашего угла зрения она всегда рисуется как круг. Почти чистые примеры сферических форм — это апельсины, луна, футбольные мячи и пузыри.
Th e sph e r e нарисовано в строке i s simp l y a ci rcle.
Конус
Конус — следующий по сложности рисунок. Это просто буква V с кружком между концами. Если смотреть под углом, круг представляет собой эллипс. Линия, проведенная от центра круглого основания до точки буквы V, является средней линией конуса.Если основание конуса перпендикулярно средней линии, стороны конуса отрисовываются от узких концов эллипса. В противном случае будет видно, что основание конуса срезано под углом. Практически чистые примеры конических форм — это карандаши, рождественские елки, корабельные мачты и шляпы ведьм.
Конус изображен в виде треугольника с эллипсом на одном конце. Линия, проведенная от середины эллипса до точки конуса, называется средней линией. Если линия, проведенная через самую широкую часть эллипса, не перпендикулярна средней линии, конус не будет стоять прямо.
C o m ple x формы можно использовать e n as c o mbin a tation he b a s i c fo r мс.
Цилиндр
Цилиндр нарисован с параллельными линиями для сторон и окружностями между параллельными линиями.(Как и в случае с конусом, круги становятся эллипсами, если смотреть под углом.) Если верх и низ цилиндра перпендикулярны его сторонам, параллельные линии проводятся от узких концов эллипсов. Линия от центра одного эллипса до центра другого — это средняя линия цилиндра. Линия, проведенная через самую широкую часть эллипса, будет перпендикулярна средней линии цилиндра. Важно помнить, что, хотя верхняя и нижняя поверхности цилиндра параллельны, они не изображаются как одинаковые эллипсы.Чем ближе одна из этих поверхностей НАХОДИТСЯ на уровне ваших глаз (также известная как линия горизонта), тем уже будет эллипс; Чем дальше от уровня глаза , тем округлее будет эллипс. (Подробнее об этом см. В главе об эллиптической перспективе.) У укороченного в ракурсе цилиндра — цилиндра, который сужается с одного конца, чтобы создать иллюзию проекции или расширения в пространство — будет казаться, что его стороны не параллельны, потому что они обращается в перспективе. В перспективе кажется, что параллельные линии сходятся, уходя в пространство.Почти чистыми примерами цилиндрических форм являются банки, ручки от метел и карнизы для штор.
A c y lin d e r i s d ra w na 9025 9025 9025 9025 9025 9025 9025 a ir из p ara llel li n e s w iith he ellipse ellipse ellipse 9025 ellipse e nd b e tween t h e pa r a llel line s . T he elli ps e n eare r to y ou r eye l e vel will 9025 a r n a rr o wer th an the o ne fa r th e r level 0259
На этом рисунке цилиндр №1 слева изображен правильно, а три других — неверно. В № 2 верхний и нижний эллипсы одинаковы, но этого не может быть, потому что они видны на разных уровнях. Цилиндр №3 неправильный, потому что, даже если он стоит на плоской поверхности, нижнюю часть не следует рисовать плоской, потому что нижняя часть самой формы изогнута. В цилиндре №4 верхний эллипс должен быть уже, потому что он ближе к уровню наших глаз, чем нижний эллипс.
Тор
Тор имеет форму бублика. Если смотреть сверху, это всего лишь два круга, один внутри другого. С точки зрения трех четвертей середина внешнего края представляет собой среднюю часть или эллипс; концы — это части двух маленьких кружков. Внутренняя часть тора (отверстие в бублике) изображена двумя дугами, которые образуют яйцевидную (овальную) форму с заостренными концами. Почти чистые примеры тора — рогалик, свернутый в спираль садовый шланг или змея и звено цепи.
Тор — это , нарисованный либо как два эллипса, один внутри другого, либо как эллипс с двумя противоположными дугами, образующими острие эллипса t ed. Видно (сбоку тор может быть две параллельные мелкие части с половиной — Окружность на с обоих концов.
Куб
Куб — это коробка с шестью квадратными сторонами. Чистыми примерами кубиков являются игральные кости, шкафы для хранения документов, навесы и стиральные машины.Куб — это самая сложная форма для правильного рисования, потому что она связана с линейной перспективой. Более подробное объяснение линейной перспективы будет представлено позже в этой книге, но на следующих страницах вы найдете некоторые основные концепции.
Куб представляет собой шестигранную форму — ; ea c сторона h — плоский квадрат . Это mo s t сложная из пяти основных форм для рисования, потому что она требует понимания линейной перспективы .
© Авторские права Билл Мартин 2007-2014 • Почтовый ящик 511, Альбион, Калифорния 95410 • info@guidetooilpainting.com
Геологическая служба США: Кратерное озеро, Орегон: Перспектива Конуса Мерриама
Вид под углом, смотрящий на север, в сторону Конуса Мерриам. Расстояние в нижней части изображения составляет около 1,8 км (1,1 мили).
Конус Мерриам, симметричный холм, сложенный андезитом, был назван в честь бывшего директора Вашингтонского института Карнеги.Особенности его поверхности и отсутствие кратера (по сравнению с шлаковым конусом Острова Волшебников) указывают на то, что он образуется под водой. Андезитовый состав конуса Мерриам похож на глубоко затопленные части острова Волшебников вулкан и к юго-востоку от центральной платформы.
На стене кальдеры к северу от конуса крутые обнажения (A) которые простираются далеко под поверхностью озера. Скамейки на обнажения, вероятно, соответствуют значительным перерывам в росте горы Мазама.Над озером такие разломы разделяют горы. извержение истории в «пакеты» лав, полученных из специальные вентиляционные отверстия для источников. Большинство скал в этой части возраст береговой линии составляет более 120 000 лет, что позволяет предположить, что самые глубокие обнажения под поверхностью происходят от ранних горных история (см. Chaski Bay и Phantom Корабль ).
На дне озера между Клитвуд-Коув и Мерриам-Коун находится углубление (B), которое отмечает примерное расположение небольшого бассейны с относительно теплой водой.Эти бассейны, открытые в 1988 г. и 1989 г. исследователями на борту одноместного подводного аппарата. корабль Deep Rover плотнее, чем вода в озере, потому что более высокой концентрации растворенных солей. Это место также отмечает область самого высокого измеренного теплового потока в Кратерном озере (Уильямс и фон Герцен, 1983).
Источник: Гарднер, Джеймс В., Питер Дартнелл, Лоран Хеллекин, Чарльз Р.Бэкон, Ларри А. Майер и Дж. Кристофер Стоун. 2001 г. Батиметрия и избранные виды в перспективе озера Кратер, штат Орегон. Отчет USGS по исследованию водных ресурсов 01-4046.
Определение конуса прогноза следа NHC
Определение конуса прогноза колеи NHC
Определение:
Конус представляет собой вероятный след центра тропического циклона и образован окружающими область, обозначенная набором кругов (не показаны) вдоль пути прогноза (в 12, 24, 36 часов и т. д.).Размер каждого круга установлен таким образом, чтобы две трети исторических ошибок официального прогноза за 5-летний период образец попадает в круг. Радиусы окружностей, определяющие конусы в 2021 году для Атлантического океана, восточной Бассейны северной части Тихого океана и центральной части северной части Тихого океана приведены в таблице ниже.
Можно также изучить исторические следы, чтобы определить, как часто остается весь 5-дневный путь циклона полностью в области конуса. Это другая точка зрения, которая игнорирует большинство ошибок синхронизации.Например, шторм, движущийся очень медленно, но в ожидаемом направлении, все равно будет в пределах области конус, даже если ошибка прогноза траектории может быть очень большой. На основе прогнозов по сравнению с предыдущими 5 лет, можно ожидать, что весь путь тропического циклона останется в пределах конуса примерно на 60-70% времени.
Радиусы кругов конусов прогноза NHC и CPHC на 2021 год, основанные на статистике ошибок за 2016-2020 годы:
Период прогноза | 2/3 Круг вероятности, | 2/3 Круг вероятности, | 2/3 Круг вероятности, |
| 12 | 27 | 25 | 34 |
| 24 | 40 | 37 | 49 |
| 36 | 55 | 51 | 66 |
| 48 | 69 | 64 | 81 |
| 60 | 86 | 77 | 95 |
| 72 | 102 | 89 | 120 |
| 96 | 148 | 114 | 137 |
| 120 | 200 | 138 | 156 |
Пример графика конуса 5-дневного прогноза трека:
.

 Для того чтобы увидеть их целиком, надо отойти дальше. Рекомендуется рисовать предметы, удаленные от точки зрения на расстояние, равное не менее полутора, двум или даже трем наибольшим их измерениям. Если же отойти от них дальше, то они будут выглядеть значительно уменьшенными, и объемность их будет мало выявлена. Отраженные от находящегося перед зрителем предмета лучи света попадают в глаз в виде пучка, имеющего форму конуса, вершина которого находится в зрачке. Поле зрения находится в пределах конуса зрения. Смотря на предметы обоими глазами, мы имеем два конуса зрения. Если смотреть на очень близко расположенный небольшой предмет только одним правым, а затем только левым глазом, то мы увидим его с разных сторон, так как зрачок правого глаза находится на некотором расстоянии от зрачка левого глаза. Когда мы смотрим на этот же, но более удаленный предмет одновременно обоими глазами, то воспринимаем его как единый объем.
Для того чтобы увидеть их целиком, надо отойти дальше. Рекомендуется рисовать предметы, удаленные от точки зрения на расстояние, равное не менее полутора, двум или даже трем наибольшим их измерениям. Если же отойти от них дальше, то они будут выглядеть значительно уменьшенными, и объемность их будет мало выявлена. Отраженные от находящегося перед зрителем предмета лучи света попадают в глаз в виде пучка, имеющего форму конуса, вершина которого находится в зрачке. Поле зрения находится в пределах конуса зрения. Смотря на предметы обоими глазами, мы имеем два конуса зрения. Если смотреть на очень близко расположенный небольшой предмет только одним правым, а затем только левым глазом, то мы увидим его с разных сторон, так как зрачок правого глаза находится на некотором расстоянии от зрачка левого глаза. Когда мы смотрим на этот же, но более удаленный предмет одновременно обоими глазами, то воспринимаем его как единый объем.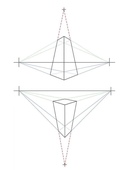 Для того чтобы четко увидеть находящийся сбоку предмет, надо изменить направление взгляда.
Для того чтобы четко увидеть находящийся сбоку предмет, надо изменить направление взгляда.