Конус вид сверху: Построение конуса с вырезом — Чертежик

Содержание

Формулы объема цилиндра, шара, конуса — площадь поверхности и основания

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу.

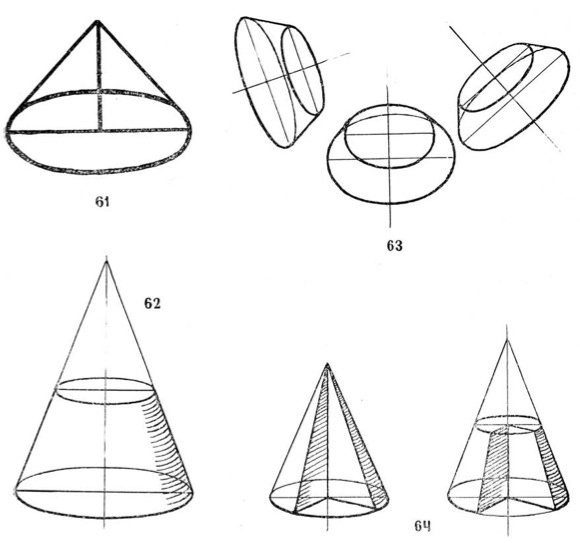Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.

Мы тоже расскажем о ней.

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Формулы объема и площади поверхности. Цилиндр, конус и шар» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Форсунки с факелом в виде полого конуса для распыливания воды и технических жидкостей

НАЗНАЧЕНИЕ

Форсунки с факелом в виде полого конуса предназначены для мелко- и среднедисперсного распыливания воды и технических жидкостей в системах доувлажнения и кондиционирования.

ОПРОСНЫЙ ЛИСТ Скачать

Общий каталог на форсунки центробежные

Форсунки с факелом в виде полого конуса типа ТР, ТФ06 и ТН

Материал форсунки — Латунь ЛС59. По специальному заказу форсунки изготавливаются из нержавеющей стали 08Х18Н (или аналога).

Тип форсунки

Эскиз

Расход жидкости (кг/ч)

Каталог форсунок

ТР45, ТР60, ТР90

11…231

ТФ06

12…90

ТН

20.

..260

ТН

60…790

ТН

175…2690

ТН

645…28500

Уважаемые коллеги!

Если Вы по каким-либо причинам не смогли подобрать для своих задач форсунки, из представленных на нашем сайте, напишите нам, и наши специалисты обязательно Вам помогут.

Пожалуйста, не забудьте при изложении Ваших требований рабочую среду и ожидаемые параметры форсунки, в том числе давление, расход, вид факела, угол раскрытия, особые требования (дисперсность и т.д.). Чем больше информации о стоящей перед Вами задаче Вы предоставите, тем точнее мы сможем реализовать Ваши пожелания.

Что такое конус? Определение, формула, свойства, примеры

Колбочки можно найти во множестве вещей, которые мы видим каждый день. Рожок для мороженого, дорожный конус и кепка на день рождения — это лишь некоторые распространенные примеры формы конуса.

Несмотря на то, что конусы в изобилии присутствуют в нашей повседневной жизни, мы все еще не можем понять основы конусов в геометрии.

Чтобы помочь вам понять чудо шишек, мы подготовили руководство, которое познакомит вас со всеми основами. Давай начнем!

Что такое конус в математике?

В математике конус определяется как характерная трехмерная геометрическая фигура с плоской изогнутой поверхностью, направленной вверх.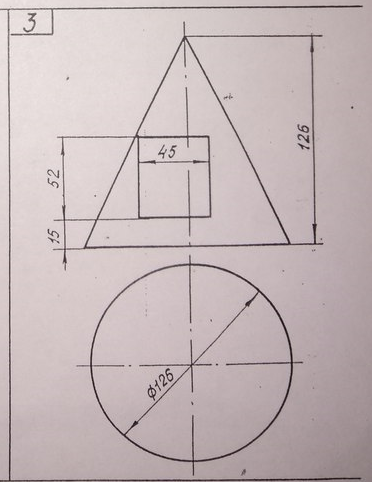 Термин «конус» происходит от греческого слова «конос», что означает клин или пик. Заостренный конец называется вершиной, а плоская поверхность называется основанием.

Три основных свойства конуса:

Он имеет одну круглую грань.
Не имеет ребер.
Имеет одну вершину (угол).

Родственные игры

Какие элементы конуса?

Тремя основными элементами конуса являются его радиус, высота и наклонная высота.

Радиус конуса

Радиус определяется как расстояние между центром круглого основания и любой точкой на окружности основания.

Высота конуса

Высота представляет собой расстояние от вершины конуса до центра круглого основания.

Высота наклона конуса

Наклонная высота конуса — это расстояние от вершины конуса до точки на внешнем краю круглого основания. Формула для наклонной высоты получена с использованием теоремы Пифагора.

Здесь l — наклонная высота конуса, r — радиус, h — высота конуса.

Связанные рабочие листы

Типы конусов

При изучении конусов в геометрии мы обычно рассматриваем правильный круглый конус. Но конус может быть двух категорий, в зависимости от положения вершины на основании:

Прямой круговой конус — это конус, вершина которого перпендикулярна основанию. Здесь ось образует прямой угол.

Если положение вершины находится где-то за пределами центра основания, это наклонный конус. Здесь ось неперпендикулярна.

Несколько интересных фактов о конусах

1. Конус и пирамида связаны между собой. Формулы их площади поверхности также схожи!

2. Наши глаза имеют 6–7 миллионов колбочек, которые помогают им приспосабливаться к цветовой чувствительности.

Конус формируется набором линий, которые соединяются с одной точкой, называемой вершиной.

Давайте изучим различные формулы, связанные с конусом, которые помогут вам решить некоторые интересные задачи в будущем.

Изогнутая поверхность конуса

Конус имеет как плоскую, так и криволинейную поверхности. Когда мы говорим о площади криволинейной поверхности конуса, это относится только к площади изогнутой части конуса, а не к круглому основанию.

Площадь криволинейной поверхности конуса определяется по формуле:

Площадь криволинейной поверхности = π ✕ r ✕ l квадратных единиц,

где r = радиус основания конуса, l = наклонная высота конуса и π = 3,14

Общая площадь поверхности конуса

Полная площадь поверхности конуса равна сумме площадей его круглого основания и криволинейной поверхности.

Площадь криволинейной поверхности конуса определяется по формуле:

Общая площадь поверхности = площадь криволинейной поверхности + площадь круглого основания

TSA = π ✕ r ✕ l + π ✕ r²

или, TSA = π ✕ r ✕ (l + r) квадратных единиц.

Объем конуса

Объем конуса в геометрии — это количество пространства, которое занимает конус. Объем конуса также можно определить как вместимость жидкости, которую может удержать конус, если бы он был полым изнутри. Поскольку конус имеет круглое основание, мы можем легко рассчитать объем конуса, измерив радиус «r» и высоту «h».

V = $\frac{1}{3}$ ✕ (π ✕ r² ✕ h) кубическая единица.

Решенные примеры

Пример 1: Найдите объем конуса, где r = 5 см и h = 7 см.

Решение : Используя формулу объема конуса, получаем:

V = (1/3)πr² h

Здесь r = 5 см, h = 7 см

V= $ \frac{1}{3}$ ✕ 3,14 ✕ 5 ✕ 5 ✕ 7

= $\frac{1}{3}$ ✕ 549,5 = 183,16 см³

Пример 2. Рассчитайте площадь криволинейной поверхности конуса, где радиус основания 8 см, высота наклона 24 см.

Решение . Мы можем найти площадь криволинейной поверхности конуса, используя формулу

Площадь криволинейной поверхности данного конуса = 3,14 ✕ 8 ✕ 24 = 602,88 см².

Пример 3: Если высота наклона конуса 25 см, а его радиус 7,5 см, найдите общую площадь поверхности конуса.

Решение :

Общая площадь поверхности конуса равна,

Общая площадь поверхности = π ✕ r ✕ (l + r)

Здесь r = 7,5 см, а l = 25 см.

Следовательно,

Общая площадь поверхности данного конуса = 3,14 ✕ 7,5 ✕ (7,5 + 25)

(32.5)

= 765,37 см²

Практические задачи

где радиус 8 см, а высота 13 см.

870,82 см³

335,54 см³

840,54 см³

820,53 см³

Правильный ответ: 870,82 см³
. Используя формулу для объема конуса, получаем: 3π16 r² ч
Здесь , r = 8 см, h = 13 см
V= $\frac{1}{3}$ ✕ 3,14 ✕ 8 ✕ 8 ✕ 13
= $\frac{1}{3}$ ✕ 2612,48 = 870,82 см³

Наклонная высота конуса 21 см, радиус 12 см. Найдите полную площадь поверхности конуса.

1298,67 см²

1349,50 см²

1243,44 см²

1344,67 см²

Правильный ответ: 1243,44 см² 12 см, а l = 21 см.
Следовательно,
Общая площадь поверхности данного конуса = 3,14 ✕ 12 ✕ (12 + 21)
= 37,68 ✕ 33
= 1243,44 см²

Найдите площадь криволинейной поверхности конуса, где r = 10 см высота 21см.

659,4 см²

782,4 см²

689 см²

679,6 см²

Правильный ответ: 659,4 см²
Площадь криволинейной поверхности конуса можно найти по формуле 10 см, l = 21 см
Следовательно,
площадь криволинейной поверхности данного конуса = 3,14 ✕ 10 ✕ 21 = 659,4 см².

Часто задаваемые вопросы

Сколько граней и вершин у конуса?

Конус имеет одну грань с одной вершиной. Заостренная вершина или вершина конуса также называется его вершиной.

Какие есть реальные примеры конусов?

Колбочки окружают нас повсюду. Шляпы, которые мы используем на вечеринках, рождественская елка, которую мы видим во время праздничных гуляний, а иногда даже морковь, которую мы едим, являются реальными примерами конуса.

Чем конус отличается от треугольника?

Конус представляет собой трехмерную геометрическую фигуру с круглым основанием и заостренным краем. Треугольник, с другой стороны, представляет собой двумерную фигуру, которая имеет три ребра и вершины.

Адаптер PowerFlare® Cone-Top — Traffic Safety Corp.

Установите фонари PowerFlare на любой стандартный дорожный конус.
Быстрая и простая установка и снятие.
Прикрепите ракеты PowerFlare с помощью магнитов или эластичных шнуров.
Загрузить техпаспорт (PDF, 272 КБ)

Узнать цену

Описание
Техническая спецификация
Видео

Описание

Области применения

Когда для управления дорожным движением, строительства или аварийных сцен требуется повышенное освещение для лучшей видимости, прожекторы PowerFlare можно установить поверх любого стандартного дорожного конуса с помощью нашего запатентованного конического адаптера (CTA-001). .

Адаптер Cone-Top может использоваться с магнитными фонарями PowerFlare, которые крепятся к внутреннему металлическому элементу, что обеспечивает быструю и легкую установку и снятие. Для немагнитных фонарей PowerFlare входящие в комплект эластичные шнуры позволяют легко закрепить свет!

Особенности

Приподнимает ракеты PowerFlare для лучшей видимости на больших расстояниях
Быстрая и простая установка и снятие
Совместим со всеми вспышками PowerFlare – магнитными и немагнитными

Магнитные раструбы PowerFlares

крепятся к внутреннему металлическому элементу адаптера Cone-Top.

Немагнитные раструбы PowerFlares крепятся к адаптеру Cone-Top с помощью прилагаемых эластичных шнуров.

Доступные комплекты включают по одному коническому адаптеру на каждую вспышку PowerFlare и доступны в упаковках по 2, 4, 8, 12 и 20 штук. Стандартные комплекты поставляются с красными, желтыми или красно-синими светодиодами желтого цвета. снаряды.

Конусные переходники также доступны в упаковках по 6, 12, 24 и 36 штук в индивидуальных сумках для переноски. Каждый адаптер Cone-Top поставляется с двумя эластичными шнурами. Доступны нестандартные количества.