Последовательность рисования дерева в теплом колорите
Класс: 3.
Тема: Последовательность рисования дерева в теплом колорите.
Тип урока: сообщение нового материала.
Цель урока: Во время урока учащиеся должны познакомится с новым термином “колорит”. Закрепить ЗУН при смешивании различных цветов, исключительно в теплом колорите красок. Воспитать к наблюдательности, внимании и усидчивости при заданной ими работой.
Оборудование учителя: План конспект, наглядное изображение, акварель, кисть, палитра.
Оборудование учащихся: Карандаш, альбом А4, акварель, кисть, палитра.
План урока.
- Организационная часть – 2 мин.
- Сообщение нового материала – 10 мин.
- Практическая часть – 30 мин.
- Заключительная часть – 3 мин.
Ход урока
Ребята, сегодня мы пройдем тему
“Последовательность рисования дерева в теплом
колорите”.
Для этого мы должны подбирать
доминирующие цвета и рисовать.
Вы наверно слово “колорит” слышите впервые. Гармоничное сочетание, взаимосвязь, тональное объединение различных цветов в картине называется колоритом. Колорит раскрывает нам красочное богатство мира. Он помогает художнику передать настроение картины: колорит может быть спокойным, радостным, тревожным, грустным и др. Колорит бывает теплым и холодным, светлым и темным.
Спокойствие
Радость
Тревога
Грусть
Светлым
Темным
Каждый художник имеет свой почерк. Кто-то любит
использовать светлые цвета, а кто-то темные.
Например, возьмем писателей. Они передают через
стихи и рассказов свои образы и взгляды с помощью
букв, а художники-живописцы передают красоту
окружающего мира с помощью красок.
Ребята, на сколько частей мы делили цвета? (Теплые, холодные)
Теплые: красные, желтые, оранжевые и все цвета, в которых имеется хотя бы частичка этих цветов. Теплые цвета напоминают цвет солнца, огня того, что в природе действительно дает тепло.
Холодные: синие, голубые, зеленые, сине-фиолетовые, сине-зеленые и цвета, которые можно получить от смещения с этими цветами. Холодные цвета ассоциируются в нашем представлении с чем-то действительно холодным льдом, снегом, водой, лунным цветом и т.п.
Практическая часть
Ребята, сегодняшняя работа делится на
несколько этапов.
Будем рисовать
последовательно.
1 этап. Рисование карандашом
Альбом (А4) держим в вертикальном положении. С вершины листа посередине проводим вспомогательную линию. На уроке линейкой не пользуемся. Примерно отметим высоту и ширину дерева. При построении дерева сначала рисуем твердым карандашом, так как линии должны быть нечеткими. Сначала рисуем дерево, потом задний фон – кусты. Кусты должны быть маленькими, так как они стоят далеко сзади.
2 этап. Подчеркивание рисунка
(рисование карандашом)
На этом этапе мы должны рисовать ветки и ствол дерева. Рисуем в небе облака. Чем ближе облака они увеличиваются (линия горизонта, воздушная перспектива)
3 этап. Покраска (акварель)
Для этого мы будем использовать теплые цвета.
Сначала берем светло-зеленый цвет и смешиваем
водой. В первую очередь будем красить дерево, а
после кусты и землю. У нас получилось картина из
одного цвета
4 этап. Тональное деление цветов
Сейчас будем делить дерево, землю, кусты на тона. Будем использовать только один цвет, разделяя их по тону: светлые и темные. Тем дальше, тем темнее. Из всех самым светлым будет земля, потом дерево и сзади стоящие кусты.
5 этап
На этом этапе будем рисовать верхушку дерева и небо.
Ствол дерева будем рисовать коричневым цветом. Для того чтобы рисовать небо смешиваем желтый цвет с водой. Небо синим цветом, опять же смешивая с водой.
Наш рисунок получился светлым, нарисованный теплыми цветами.
Ребята, что вы узнали нового на этом уроке? Как вы поняли слово “колорит”?
7.
Рисование деревьев и кустов.В рисовании дерева, как и любой другой натуры, существует этапность. Сначала мы изображаем ствол и, учитывая, что дерево растет из земли, намечаем легкими штрихами ее поверхность. Затем намечаем высоту выбранной натуры и ее характер. Далее намечаем толщину ствола у земли и прослеживаем, как он постепенно сужается к верхушке до тонких веточек. Плавными линиями отмечаем поочередное расположение крупных ветвей, определяя их длину, направление, с ответвлениями от них мелких веток. Намечаем толщину крупных веток и прослеживаем с помощью карандаша их соединение со стволом.
На
протяжении всего процесса рисования
необходимо помнить о том, что дерево —
это своеобразный сложный объем и
некоторые ветки расположены ближе,
другие дальше от нас. В зависимости от
этого, чтобы правдиво передать пространство
в рисунке и чтобы изображение не было
плоским и неинтересным, те элементы,
которые расположены ближе к нам, мы
прорисовываем более четко, в полную
силу карандаша, постепенно ослабляя ее
при изображении дальних планов.
У куста, в отличие от дерева, единого ствола нет — вместо него мы наблюдаем невысокие древовидные стебли, растущие от одного корня. Но у каждого кустарника своя пластика ветвей, как и у дерева: они то угловатые и хаотичные, как у терновника, то плавные и направленные к свету, как у ракиты.
Таким образом, наблюдая особенности строения деревьев и кустарников, с изобразительной точки зрения следует выделить основные моменты, которые определят характер дерева каждой породы, его внешнего облика. Это ствол, главные ветви, мелкие веточки и листва. Ставя перед собой задачу нарисовать дерево или куст, необходимо выделить три главных этапа.
1. Изображение натуры начинается снизу, от корней в сторону роста, с нанесением легких вспомогательных линий, ритмических осей, направляющих основное движение ствола и примыкающих к нему ветвей и веточек.
2.
Намечается обычная масса силуэта всей
кроны, детально прорисовывается легким
касанием карандаша пластика составляющих
элементов натуры.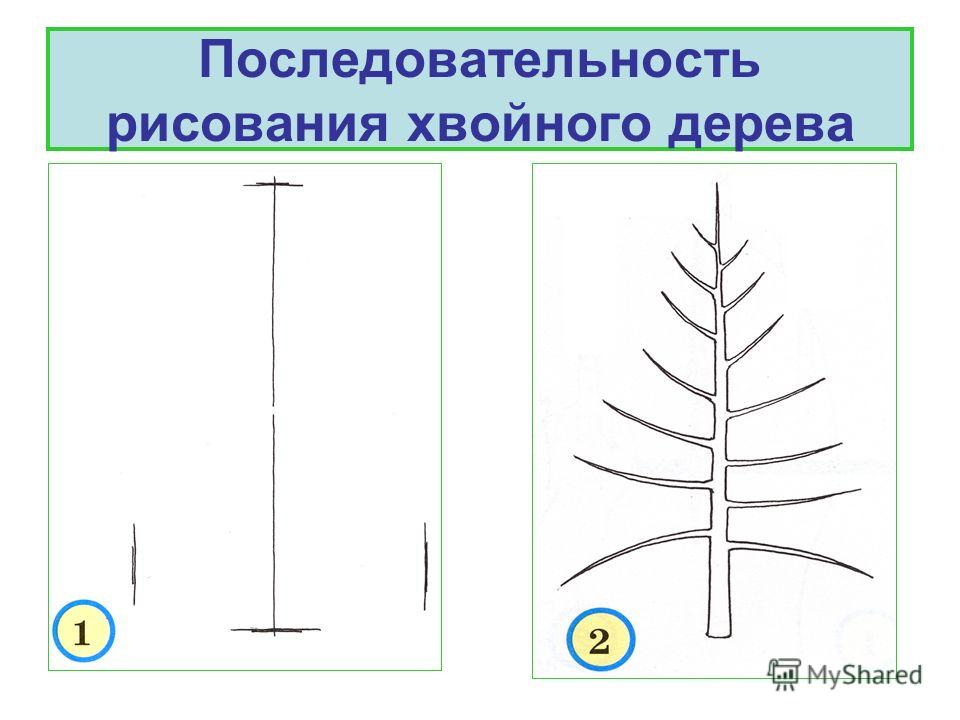
3. Уточняется обычная масса кроны, прорисовываются видимые части ствола дерева и веток, объединяются отдельные части кроны в одно целое, наносится посредством штриховки светотень отдельных масс листвы, ствола, веток, придавая объем изображаемому.
28 Основные, составные цвета. Локальный цвет. Законы цветового контраста и нюанса.
Все цвета цветового круга-храматические.
3осн. Цвета: красный (К), синий (С), желтый(Ж).
Составные цвета:
К+Ж=Оранжевый
Ж+С=Зеленый
С+К=Фиолетовый
Все цвета: теплые (К,О,Ж,Ж-З с цветом сонца огня тепла)
Холодные (С,Г,Ф,С-З- вода, лед, снег, т.е. холод).
Закон цветового контраста:
Пары контрастных цветов:
К-З
О-С
Ж_Ф
Закон цветового нюанса:
Это
плавный переход одного цвета в другой,
мягко сближена цветовая гамма.
Что такое последовательность Фибоначчи?
Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
Семена подсолнуха имеют золотую спираль, которая связана с последовательностью Фибоначчи. (Изображение предоставлено: Белтерц/Getty Images)Последовательность Фибоначчи — это ряд чисел, в котором каждое число является суммой двух предшествующих ему чисел. Начиная с 0 и 1, первые 10 чисел последовательности выглядят так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее до бесконечности. Последовательность Фибоначчи можно описать с помощью математического уравнения: Xn+2= Xn+1 + Xn
Люди утверждают, что у числовой последовательности есть много особых свойств, например тот факт, что это «секретный код природы» для создания совершенных структур, таких как Великая пирамида в Гизе или культовая морская ракушка, которая, вероятно, украшала обложку вашего школа математика учебник.
Но многое из этого неверно, и истинная история сериала немного более приземленная.
Кто открыл последовательность Фибоначчи?
Первое, что нужно знать, это то, что эта последовательность изначально не принадлежала Фибоначчи, который на самом деле никогда не носил этого имени. Итальянский математик, которого мы называем Леонардо Фибоначчи, родился около 1170 года и первоначально был известен как Леонардо Пизанский, сказал Кит Девлин, математик из Стэнфордского университета.
Только в 19 веке историки придумали прозвище Фибоначчи (примерно означающее «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского, сказал Девлин.
Почетный математик Стэнфордского университета Кит Девлин — почетный математик Стэнфордского университета, соучредитель и почетный исполнительный директор Стэнфордского института H-STAR, соучредитель Стэнфордской исследовательской сети mediaX и почетный старший научный сотрудник Центр изучения языка и информации.
Он является членом Всемирного экономического форума, членом Американской ассоциации содействия развитию науки и членом Американского математического общества. Он написал 33 книги и более 80 исследовательских статей.
Подробнее: Большие числа, определяющие Вселенную
Леонардо Пизанский на самом деле не открыл эту последовательность, сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски нового математического гения». Кто изменил мир» (Princeton University Press, 2017). Древние санскритские тексты, в которых использовалось число – это индуистско-арабская система счисления , впервые упоминаются в 200 году до н. э. на несколько столетий раньше Леонардо Пизанского.
«Это было всегда, — сказал Девлин Live Science.
Портрет Леонардо Фибоначчи, который, как считается, открыл знаменитую последовательность Фибоначчи. Однако в 1202 году в массивном томе он вводит последовательность с проблемой, связанной с кроликами.
(Изображение предоставлено: Stefano Bianchetti/Corbis через Getty Images)Однако в 1202 году Леонардо Пизанский опубликовал массивный фолиант «Liber Abaci», математическую «поваренную книгу о том, как выполнять вычисления», — сказал Девлин. . «Liber Abaci», написанная для торговцев, изложила индийско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков по кредитам и так далее, добавил он.
В одном месте книги Леонардо Пизанский вводит последовательность с задачей, включающей кроликов . Задача выглядит следующим образом: начните с самца и самки кролика. Через месяц они созревают и производят помет с еще одним кроликом-самцом и самкой. Месяц спустя эти кролики размножаются, и, как вы уже догадались, появляются еще один самец и самка, которые также могут спариваться через месяц. (Не обращайте внимания на крайне неправдоподобную биологию.) Сколько кроликов у вас будет через год?
Ответ, как оказалось, равен 144, и формула, которая использовалась для получения этого ответа, теперь известна как последовательность Фибоначчи.
Подробнее: 9 уравнений, которые изменили мир
«Liber Abaci» впервые представила последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо Пизанский больше никогда не упоминал об этой последовательности. На самом деле, о нем почти забыли до 19 века, когда математики больше проработали математические свойства последовательности. По словам Девлина, в 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи».
Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но они не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)(открывается в новой вкладке)
Почему важна последовательность Фибоначчи?
Помимо того, что последовательность Фибоначчи является прекрасным учебным пособием, она встречается в нескольких местах в природе.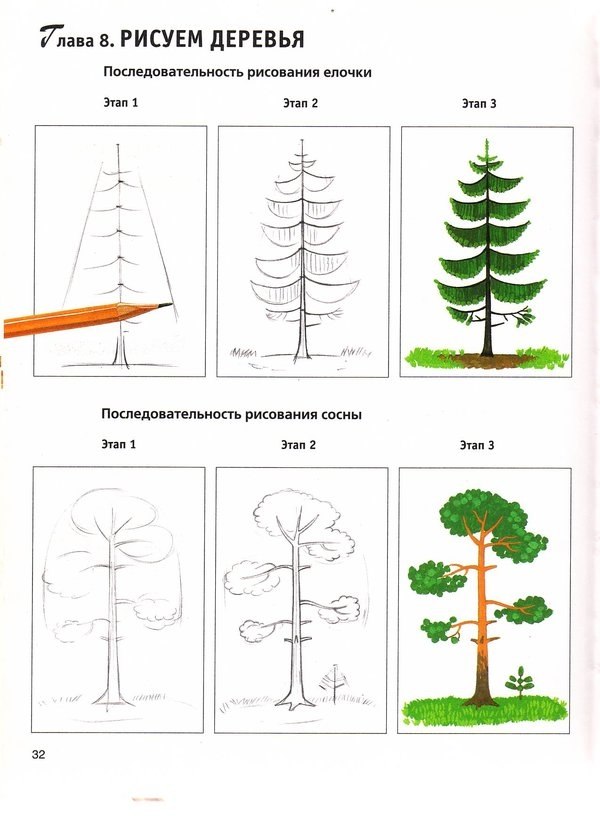
Однако Девлин сказал, что это не какой-то секретный код, управляющий архитектурой вселенной.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение, phi , иррациональное число , у которого много собственных сомнительных знаний. Отношение последовательных чисел в последовательности Фибоначчи становится все ближе к золотому сечению, которое равно 1,6180339887498948482…
Подробнее: типы роста растений, сказал Девлин. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнуха, согласно «9».0007 Phyllotaxis: A Systemic Study in Plant Morphogenesis » (Cambridge University Press, 1994). Но существует столько же растений, которые не следуют этому правилу.
«Это не единственное правило Бога для выращивание вещей, скажем так, — сказал Девлин.
Существуют ли примеры последовательности Фибоначчи в реальной жизни? «В соответствии с последовательностью Фибоначчи, — добавил он.
— Когда люди начинают проводить связи с человеческое тело , искусство и архитектура, ссылки на последовательность Фибоначчи из незначительных превращаются в совершенно вымышленные.«Потребуется большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — Джордж Марковски, математик, работавший в то время в Университете штата Мэн, . написал в статье 1992 года в журнале College Mathematics Journal.
Большая часть этой дезинформации может быть приписана книге 1855 года немецкого психолога Адольфа Цейзинга под названием «Эстетические исследования». Зейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. В последующие годы золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения.
С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, Леонардо да Винчи «Витрувианского человека» и множества зданий эпохи Возрождения.
По словам Девлина, всеохватывающие утверждения о том, что это соотношение «уникально приятно» для человеческого глаза, были сформулированы некритически. Он добавил, что все эти утверждения при проверке оказываются в значительной степени ложными.
«Мы умеем распознавать образы. Мы можем видеть узор независимо от того, есть он там или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».
Примечание редактора: Адам Манн внес свой вклад в эту статью .
Первоначально опубликовано на Live Science .
Тиа — главный редактор, а ранее — старший писатель журнала Live Science. Ее работы публиковались в журналах Scientific American, Wired.com и других изданиях. Она имеет степень магистра биоинженерии Вашингтонского университета, диплом о высшем образовании в области научного письма Калифорнийского университета в Санта-Круз и степень бакалавра машиностроения Техасского университета в Остине. Тиа была частью команды журнала Milwaukee Journal Sentinel, которая опубликовала серию «Пустые колыбели» о преждевременных родах, получившую множество наград, в том числе медаль Кейси 2012 года за заслуги перед журналистикой.
Рисование бинарного дерева на основе последовательности обхода
Задавать вопрос
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 3к раз
$\begingroup$
Мне дана последовательность символов из предварительного обхода двоичного дерева. Мне не дан двоичный файл, но мне нужно нарисовать двоичное дерево на основе последовательности символов из обходов
Из этого двоичного дерева обход по предварительному заказу:
NZLADRUGBY
Обход по порядку:
ALDZNURYBG
Я думал, что последовательность обхода в предварительном порядке будет проще всего вывести бинарное дерево, и я обнаружил, что дерево имеет высоту 3, и из обхода в предварительном порядке я вижу, что корнем будет N, а слева поддерево будет Z, но после этого я не уверен, что делать, так как есть вероятность, что одно поддерево может быть пустым и т.
д.
Есть ли более простой способ сделать это?
$\endgroup$
$\begingroup$
Из последовательности предварительного заказа вы знаете, что корнем является N. Затем последовательность в порядке говорит вам, что A, L, D и Z находятся в левом поддереве, а U, R, Y, B и G находятся в правом поддереве. Теперь вернитесь к последовательности предварительного заказа: она говорит вам, что Z — это корень левого поддерева. Затем последовательность в порядке говорит вам, что все три других узла левого поддерева находятся слева от Z. Таким образом, у Z нет правого потомка, а последовательность в прямом порядке говорит вам, что L является его левым потомком. Затем обе последовательности подтверждают, что A является левым дочерним элементом, а D — правым дочерним элементом L, а последовательность предварительного порядка сообщает вам, что R является корнем правого поддерева. В этот момент у вас есть такая часть дерева:
Н
/ \
З Р
/
л
/ \
А Д
Продолжайте в том же духе, и вы сможете закончить построение дерева без особых проблем.