Pngtree PNG рисунок и векторы картинки
Силуэт стрекоза
милый привет сентябрь текстовое изображение
акварель мультфильм растет дерево
Симпатичная мусульманская иллюстрация шеф повара для счастливого дня труда на прозрачном фоне
значок напиток апельсиновый сок
Всемирный день сердца 2022 г
мальчик читает книги
развевающийся флаг сша с текстурой
loy krathong разные цвета цветов лотоса на воде
акварельные мультяшные утки в ванне
Национальный день Саудовской Аравии дизайн с силуэтом города
Новогодняя Вечеринка Пожелания Модном Стиле Черное Золото Плакат
всплывающее диалоговое окно представления бизнес элементов
маркетинговый анализ бизнеса
черная пятница со значком стрелки
тыква в виде вампира
рамка из коричневых листьев
рыба динозавр
желтый уведомление колокольчик 3d значок рендеринга
английский алфавит i для векторной иллюстрации инъекций
одобрить кнопка галочка галочка да символ положительный принять значок изолированный клипарт
синий современный шаблон дизайна удостоверения личности
тыква в хэллоуин
Призрачный череп тыквенный фонарь хэллоуин мультяшный бордюр
тыква Хэллоуина ужасно
абстрактный радужный вихревой эффект дыма
2023 год почерк
значок телевизора наброски hd
английский алфавит p для векторной иллюстрации грушевой корзины
Октоберфест рисованной элементы иллюстрации
Проект Хэллоуина
милая иллюстрация бортпроводника с простым самолетом для приветствия дня труда
бело синий дизайн визитной карточки
вечеринка флаги цветная бумага треугольные флаги собраны и украшены гирляндами с днем рождения
нижняя третья иллюстрация
лента баннер синий клипарт дизайн изолированные
простая радужная рамка
Первомайская детская уборка
Золотая градиентная геометрия с плавающей точкой
Милая радуга
Бархатцы Венок Горизонтальные Иллюстрации Празднования
кофейные зерна реалистично
круг золотая рамка
Национальный день Саудовской Аравии twibbon с рамными воротами
свадебная рамка цветы акварель
черная пятница с красной биркой
бутылка с ядом с векторной иллюстрацией тюбетейки
счастливая осень зеленый лист концепция cirlce подарок праздник
Простой дизайн векторного удостоверения личности
сывороточный протеин
B-tree / Хабр
Введение
Деревья представляют собой структуры данных, в которых реализованы операции над динамическими множествами. Из таких операций хотелось бы выделить — поиск элемента, поиск минимального (максимального) элемента, вставка, удаление, переход к родителю, переход к ребенку. Таким образом, дерево может использоваться и как обыкновенный словарь, и как очередь с приоритетами.
Из таких операций хотелось бы выделить — поиск элемента, поиск минимального (максимального) элемента, вставка, удаление, переход к родителю, переход к ребенку. Таким образом, дерево может использоваться и как обыкновенный словарь, и как очередь с приоритетами.
Основные операции в деревьях выполняются за время пропорциональное его высоте. Сбалансированные деревья минимизируют свою высоту (к примеру, высота бинарного сбалансированного дерева с n узлами равна log n). Большинство знакомо с такими сбалансированными деревьями, как «красно-черное дерево», «AVL-дерево», «Декартово дерево», поэтому не будем углубляться.
В чем же проблема этих стандартных деревьев поиска? Рассмотрим огромную базу данных, представленную в виде одного из упомянутых деревьев. Очевидно, что мы не можем хранить всё это дерево в оперативной памяти => в ней храним лишь часть информации, остальное же хранится на стороннем носителе (допустим, на жестком диске, скорость доступа к которому гораздо медленнее).
B-деревья также представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Но, в отличие от остальных деревьев, они созданы специально для эффективной работы с дисковой памятью (в предыдущем примере – сторонним носителем), а точнее — они минимизируют обращения типа ввода-вывода.
Структура
При построении B-дерева применяется фактор t, который называется минимальной степенью. Каждый узел, кроме корневого, должен иметь, как минимум t – 1, и не более 2t – 1 ключей. Обозначается n[x] – количество ключей в узле x.
Ключи в узле хранятся в неубывающем порядке. Если x не является листом, то он имеет n[x] + 1 детей. Если занумеровать ключи в узле x, как k[i], а детей c[i], то для любого ключа в поддереве с корнем c[i] (пусть k1), выполняется следующее неравенство – k[i-1] ≤k1≤k[i] (для c[0]: k[i-1] = -∞, а для c[n[x]]: k[i] = +∞). Таким образом, ключи узла задают диапазон для ключей их детей.
Таким образом, ключи узла задают диапазон для ключей их детей.
Все листья B-дерева должны быть расположены на одной высоте, которая и является высотой дерева. Высота B-дерева с n ≥ 1 узлами и минимальной степенью t ≥ 2 не превышает logt(n+1). Это очень важное утверждение (почему – мы поймем чуть позже)!
h ≤ logt((n+1)/2) — логарифм по основанию t.
Операции, выполнимые с B-деревом
Поиск
Поиск в B-дереве очень схож с поиском в бинарном дереве, только здесь мы должны сделать выбор пути к потомку не из 2 вариантов, а из нескольких. В остальном — никаких отличий. На рисунке ниже показан поиск ключа 27. Поясним иллюстрацию (и соответственно стандартный алгоритм поиска):
- Идем по ключам корня, пока меньше необходимого. В данном случае дошли до 31.
- Спускаемся к ребенку, который находится левее этого ключа.

- Идем по ключам нового узла, пока меньше 27. В данном случае – нашли 27 и остановились.
Операция поиска выполняется за время O(t logt n), где t – минимальная степень. Важно здесь, что дисковых операций мы совершаем всего лишь O(logt n)!
Добавление
В отличие от поиска, операция добавления существенно сложнее, чем в бинарном дереве, так как просто создать новый лист и вставить туда ключ нельзя, поскольку будут нарушаться свойства B-дерева. Также вставить ключ в уже заполненный лист невозможно => необходима операция разбиения узла на 2. Если лист был заполнен, то в нем находилось 2t-1 ключей => разбиваем на 2 по t-1, а средний элемент (для которого t-1 первых ключей меньше его, а t-1 последних больше) перемещается в родительский узел. Соответственно, если родительский узел также был заполнен – то нам опять приходится разбивать. И так далее до корня (если разбивается корень – то появляется новый корень и глубина дерева увеличивается).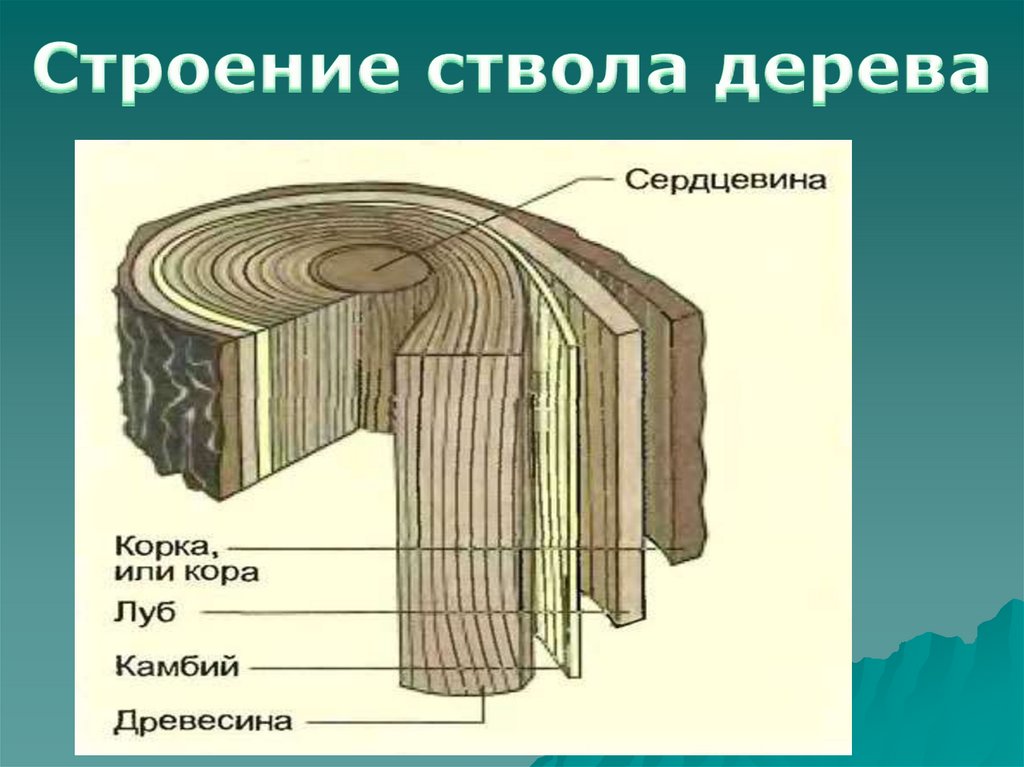 Как и в случае обычных бинарных деревьев, вставка осуществляется за один проход от корня к листу. На каждой итерации (в поисках позиции для нового ключа – от корня к листу) мы разбиваем все заполненные узлы, через которые проходим (в том числе лист). Таким образом, если в результате для вставки потребуется разбить какой-то узел – мы уверены в том, что его родитель не заполнен!
Как и в случае обычных бинарных деревьев, вставка осуществляется за один проход от корня к листу. На каждой итерации (в поисках позиции для нового ключа – от корня к листу) мы разбиваем все заполненные узлы, через которые проходим (в том числе лист). Таким образом, если в результате для вставки потребуется разбить какой-то узел – мы уверены в том, что его родитель не заполнен!
На рисунке ниже проиллюстрировано то же дерево, что и в поиске (t=3). Только теперь добавляем ключ «15». В поисках позиции для нового ключа мы натыкаемся на заполненный узел (7, 9, 11, 13, 16). Следуя алгоритму, разбиваем его – при этом «11» переходит в родительский узел, а исходный разбивается на 2. Далее ключ «15» вставляется во второй «отколовшийся» узел. Все свойства B-дерева сохраняются!
Операция добавления происходит также за время O(t logt n). Важно опять же, что дисковых операций мы выполняем всего лишь O(h), где h – высота дерева.
Удаление
Удаление ключа из B-дерева еще более громоздкий и сложный процесс, чем вставка.
1)Если удаление происходит из листа, то необходимо проверить, сколько ключей находится в нем. Если больше t-1, то просто удаляем и больше ничего делать не нужно. Иначе, если существует соседний лист (находящийся рядом с ним и имеющий такого же родителя), который содержит больше t-1 ключа, то выберем ключ из этого соседа, который является разделителем между оставшимися ключами узла-соседа и исходного узла (то есть не больше всех из одной группы и не меньше всех из другой). Пусть это ключ k1. Выберем ключ k2 из узла-родителя, который является разделителем исходного узла и его соседа, который мы выбрали ранее. Удалим из исходного узла нужный ключ (который необходимо было удалить), спустим k2 в этот узел, а вместо k2 в узле-родителе поставим k1.

Рис. 1.
2)Теперь рассмотрим удаление из внутреннего узла x ключа k. Если дочерний узел, предшествующий ключу k содержит больше t-1 ключа, то находим k1 – предшественника k в поддереве этого узла. Удаляем его (рекурсивно запускаем наш алгоритм). Заменяем k в исходном узле на k1. Проделываем аналогичную работу, если дочерний узел, следующий за ключом k, имеет больше t-1 ключа. Если оба (следующий и предшествующий дочерние узлы) имеют по t-1 ключу, то объединяем этих детей, переносим в них k, а далее удаляем k из нового узла (рекурсивно запускаем наш алгоритм). Если сливаются 2 последних потомка корня – то они становятся корнем, а предыдущий корень освобождается.
Рис.2.
Операция удаления происходит за такое же время, что и вставка O(t logt n). Да и дисковых операций требуется всего лишь O(h), где h – высота дерева.
Итак, мы убедились в том, что B-дерево является быстрой структурой данных (наряду с такими, как красно-черное, АВЛ). И еще одно важное свойство, которое мы получили, рассмотрев стандартные операции, – автоматическое поддержание свойства сбалансированности – заметим, что мы нигде не балансируем его специально.
Базы Данных
Проанализировав, вместе со скоростью выполнения, количество проведенных операций с дисковой памятью, мы можем сказать, что B-дерево несомненно является более выгодной структурой данных для случаев, когда мы имеем большой объем информации.
Очевидно, увеличивая t (минимальную степень), мы увеличиваем ветвление нашего дерева, а следовательно уменьшаем высоту! Какое же t выбрать? — Выбираем согласно размеру оперативной памяти, доступной нам (т. е. сколько ключей мы можем единовременно просматривать). Обычно это число находится в пределах от 50 до 2000. Разберёмся, что же дает нам ветвистость дерева на стандартном примере, который используется во всех статьях про B-tree. Пусть у нас есть миллиард ключей, и t=1001. Тогда нам потребуется всего лишь 3 дисковые операции для поиска любого ключа! При этом учитываем, что корень мы можем хранить постоянно. Теперь видно, на сколько это мало!
е. сколько ключей мы можем единовременно просматривать). Обычно это число находится в пределах от 50 до 2000. Разберёмся, что же дает нам ветвистость дерева на стандартном примере, который используется во всех статьях про B-tree. Пусть у нас есть миллиард ключей, и t=1001. Тогда нам потребуется всего лишь 3 дисковые операции для поиска любого ключа! При этом учитываем, что корень мы можем хранить постоянно. Теперь видно, на сколько это мало!
Также, мы читаем не отдельные данные с разных мест, а целыми блоками. Перемещая узел дерева в оперативную память, мы перемещаем выделенный блок последовательной памяти, поэтому эта операция достаточно быстро работает.
Соответственно, мы имеем минимальную нагрузку на сервер, и при этом малое время ожидания. Эти и другие описанные преимущества позволили B-деревьям стать основой для индексов, базирующихся на деревьях в СУБД.
Upd: визуализатор
Литература
«Алгоритмы. Построение и анализ» Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн (второе издание)
«Искусство программирование. Сортировка и поиск» Дональд Кнут.
Сортировка и поиск» Дональд Кнут.
Композит
Эй, я только что снизил цены на все товары. Давайте подготовим наши навыки программирования к эпохе после COVID. Проверьте это »
/ Шаблоны проектирования / Структурные модели
Также известен как: Дерево объектов
IntentComposite — это структурный шаблон проектирования, который позволяет объединять объекты в древовидные структуры, а затем работать с этими структурами, как если бы они были отдельными объектами.
ПроблемаИспользование составного шаблона имеет смысл только в том случае, если базовая модель вашего приложения может быть представлена в виде дерева.
Например, представьте, что у вас есть два типа объектов: Товары и Коробки . Ящик
Ящик может содержать несколько продуктов , а также несколько меньших ящиков . Эти маленькие коробки также могут содержать несколько продуктов или даже меньшие коробки и так далее.
Допустим, вы решили создать систему заказов, использующую эти классы. Заказы могут содержать как простые товары без какой-либо упаковки, так и коробки с продуктами… и другие коробки. Как бы вы определили общую стоимость такого заказа?
Заказ может состоять из различных продуктов, упакованных в коробки, которые упакованы в большие коробки и так далее. Вся конструкция выглядит как перевернутое дерево.
Вы можете попробовать прямой подход: разверните все коробки, просмотрите все продукты и подсчитайте сумму. Это было бы выполнимо в реальном мире; но в программе это не так просто, как запустить цикл. Вы должны знать классы Товары и Ящики , которые вы перебираете, уровень вложенности ящиков и прочие неприятные подробности заранее. Все это делает прямой подход либо слишком неудобным, либо даже невозможным.
Все это делает прямой подход либо слишком неудобным, либо даже невозможным.
Составной шаблон предполагает, что вы работаете с продуктами и ящиками через общий интерфейс, который объявляет метод расчета общей цены.
Как работает этот метод? Для продукта он просто возвращает цену продукта. Для коробки он просматривает каждый предмет, содержащийся в коробке, спрашивает его цену, а затем возвращает общую сумму для этой коробки. Если бы одним из этих предметов была коробка меньшего размера, эта коробка также начала бы перебирать свое содержимое и так далее, пока не были бы рассчитаны цены всех внутренних компонентов. Коробка может даже добавить некоторые дополнительные расходы к окончательной цене, например стоимость упаковки.
Шаблон Composite позволяет рекурсивно запускать поведение для всех компонентов дерева объектов.
Наибольшее преимущество этого подхода заключается в том, что вам не нужно заботиться о конкретных классах объектов, составляющих дерево. Вам не нужно знать, является ли объект простым продуктом или сложной коробкой. Вы можете работать с ними одинаково через общий интерфейс. Когда вы вызываете метод, объекты сами передают запрос вниз по дереву.
Вам не нужно знать, является ли объект простым продуктом или сложной коробкой. Вы можете работать с ними одинаково через общий интерфейс. Когда вы вызываете метод, объекты сами передают запрос вниз по дереву.
Пример военной постройки.
Армии большинства стран имеют иерархическую структуру. Армия состоит из нескольких дивизий; дивизия — это совокупность бригад, а бригада состоит из взводов, которые могут быть разбиты на отделения. Наконец, отряд — это небольшая группа настоящих солдат. Приказы отдаются наверху иерархии и передаются на каждый уровень до тех пор, пока каждый солдат не узнает, что нужно делать.
СтруктураИнтерфейс компонента описывает операции, общие как для простых, так и для сложных элементов дерева.
Лист — это базовый элемент дерева, не имеющий подэлементов.
Обычно конечные компоненты выполняют большую часть реальной работы, поскольку им некому делегировать эту работу.

Контейнер (он же составной ) — это элемент, который имеет подэлементы: листья или другие контейнеры. Контейнер не знает конкретных классов своих потомков. Работает со всеми подэлементами только через интерфейс компонента.
При получении запроса контейнер делегирует работу своим подэлементам, обрабатывает промежуточные результаты и затем возвращает конечный результат клиенту.
Клиент работает со всеми элементами через интерфейс компонента. В результате клиент может одинаково работать как с простыми, так и со сложными элементами дерева.
В этом примере шаблон Composite позволяет реализовать наложение геометрических фигур в графическом редакторе.
Пример редактора геометрических фигур.
Класс CompoundGraphic — это контейнер, который может содержать любое количество подформ, включая другие составные формы. Составная форма имеет те же методы, что и простая форма. Однако вместо того, чтобы делать что-то самостоятельно, составная фигура рекурсивно передает запрос всем своим дочерним элементам и «суммирует» результат.
Составная форма имеет те же методы, что и простая форма. Однако вместо того, чтобы делать что-то самостоятельно, составная фигура рекурсивно передает запрос всем своим дочерним элементам и «суммирует» результат.
Клиентский код работает со всеми фигурами через единый интерфейс, общий для всех классов фигур. Таким образом, клиент не знает, работает ли он с простой формой или сложной. Клиент может работать с очень сложными структурами объектов, не привязываясь к конкретным классам, формирующим эту структуру.
// Интерфейс компонента объявляет общие операции для обоих
// простые и сложные объекты композиции.
Интерфейс Графика есть
метод переместить (х, у)
метод рисования()
// Листовой класс представляет конечные объекты композиции. А
// листовой объект не может иметь подобъектов. Обычно это лист
// объекты, выполняющие реальную работу, а только составные объекты
// делегировать их подкомпонентам.
класс Dot реализует графику
поле х, у
конструктор Dot(x, y) { . .. }
метод move(x, y)
это.х += х, это.у += у
метод draw() есть
// Нарисуйте точку в точках X и Y.
// Все классы компонентов могут расширять другие компоненты.
класс Circle extends Dot is
радиус поля
конструктор Circle(x, y, радиус) { ... }
метод draw() есть
// Нарисуйте окружность по X и Y с радиусом R.
// Составной класс представляет сложные компоненты, которые могут
// есть дети. Составные объекты обычно делегируют фактическую
// работаем со своими детьми, а потом "суммируем" результат.
класс CompoundGraphic реализует графику
дочерние поля: массив графических
// Составной объект может добавлять или удалять другие компоненты
// (как простой, так и сложный) в или из его дочернего списка.
метод add(child: Graphic)
// Добавляем дочерний элемент в массив дочерних элементов.
метод удаления (дочерний элемент: графика)
// Удалить дочерний элемент из массива дочерних элементов.
метод move(x, y)
foreach (ребенок в детях) делать
ребенок.
.. }
метод move(x, y)
это.х += х, это.у += у
метод draw() есть
// Нарисуйте точку в точках X и Y.
// Все классы компонентов могут расширять другие компоненты.
класс Circle extends Dot is
радиус поля
конструктор Circle(x, y, радиус) { ... }
метод draw() есть
// Нарисуйте окружность по X и Y с радиусом R.
// Составной класс представляет сложные компоненты, которые могут
// есть дети. Составные объекты обычно делегируют фактическую
// работаем со своими детьми, а потом "суммируем" результат.
класс CompoundGraphic реализует графику
дочерние поля: массив графических
// Составной объект может добавлять или удалять другие компоненты
// (как простой, так и сложный) в или из его дочернего списка.
метод add(child: Graphic)
// Добавляем дочерний элемент в массив дочерних элементов.
метод удаления (дочерний элемент: графика)
// Удалить дочерний элемент из массива дочерних элементов.
метод move(x, y)
foreach (ребенок в детях) делать
ребенок. двигаться (х, у)
// Композит выполняет свою основную логику в конкретном
// путь. Он рекурсивно проходит через всех своих потомков,
// сбор и подведение их итогов. Поскольку
// потомки композита передают эти вызовы своим
// дочерние элементы и т. д., просматривается все дерево объектов
// как результат.
метод draw() есть
// 1. Для каждого дочернего компонента:
// - Нарисовать компонент.
// - Обновить ограничивающий прямоугольник.
// 2. Нарисуйте пунктирный прямоугольник, используя ограничивающий
// координаты.
// Клиентский код работает со всеми компонентами через их базу
// интерфейс. Таким образом, клиентский код может поддерживать простой лист.
// компоненты, а также сложные композиты.
класс ImageEditor
поле все: CompoundGraphic
метод загрузки ()
все = новый CompoundGraphic()
all.add (новая точка (1, 2))
all.add(новый круг(5, 3, 10))
// ...
// Объединение выбранных компонентов в один сложный композит
// составная часть.
двигаться (х, у)
// Композит выполняет свою основную логику в конкретном
// путь. Он рекурсивно проходит через всех своих потомков,
// сбор и подведение их итогов. Поскольку
// потомки композита передают эти вызовы своим
// дочерние элементы и т. д., просматривается все дерево объектов
// как результат.
метод draw() есть
// 1. Для каждого дочернего компонента:
// - Нарисовать компонент.
// - Обновить ограничивающий прямоугольник.
// 2. Нарисуйте пунктирный прямоугольник, используя ограничивающий
// координаты.
// Клиентский код работает со всеми компонентами через их базу
// интерфейс. Таким образом, клиентский код может поддерживать простой лист.
// компоненты, а также сложные композиты.
класс ImageEditor
поле все: CompoundGraphic
метод загрузки ()
все = новый CompoundGraphic()
all.add (новая точка (1, 2))
all.add(новый круг(5, 3, 10))
// ...
// Объединение выбранных компонентов в один сложный композит
// составная часть. метод groupSelected (компоненты: массив графики)
группа = новый CompoundGraphic()
foreach (компонент в компонентах) делать
group.add(компонент)
все.удалить(компонент)
все.добавить(группа)
// Будут отрисованы все компоненты.
все.рисовать()
метод groupSelected (компоненты: массив графики)
группа = новый CompoundGraphic()
foreach (компонент в компонентах) делать
group.add(компонент)
все.удалить(компонент)
все.добавить(группа)
// Будут отрисованы все компоненты.
все.рисовать()
ПрименимостьИспользуйте шаблон Composite, когда необходимо реализовать древовидную структуру объекта.
Шаблон Composite предоставляет два основных типа элементов с общим интерфейсом: простые листья и сложные контейнеры. Контейнер может состоять как из листьев, так и из других контейнеров. Это позволяет создавать вложенную структуру рекурсивных объектов, напоминающую дерево.
Используйте шаблон, если вы хотите, чтобы клиентский код одинаково обрабатывал как простые, так и сложные элементы.
Все элементы, определенные шаблоном Composite, имеют общий интерфейс. Используя этот интерфейс, клиенту не нужно беспокоиться о конкретном классе объектов, с которыми он работает.
Используя этот интерфейс, клиенту не нужно беспокоиться о конкретном классе объектов, с которыми он работает.
Убедитесь, что основная модель вашего приложения может быть представлена в виде древовидной структуры. Попробуйте разбить его на простые элементы и контейнеры. Помните, что контейнеры должны содержать как простые элементы, так и другие контейнеры.
Объявите интерфейс компонента со списком методов, подходящих как для простых, так и для сложных компонентов.
Создайте конечный класс для представления простых элементов. Программа может иметь несколько разных конечных классов.
Создайте класс контейнера для представления сложных элементов. В этом классе предоставьте поле массива для хранения ссылок на вложенные элементы. Массив должен иметь возможность хранить как листья, так и контейнеры, поэтому убедитесь, что он объявлен с типом интерфейса компонента.

При реализации методов интерфейса компонента помните, что контейнер должен делегировать большую часть работы подэлементам.
Наконец, определите методы добавления и удаления дочерних элементов в контейнере.
Имейте в виду, что эти операции могут быть объявлены в интерфейсе компонента. Это нарушило бы принцип разделения интерфейса , потому что методы в листовом классе будут пустыми. Однако клиент сможет относиться ко всем элементам одинаково, даже при составлении дерева.
- Вы можете более удобно работать со сложными древовидными структурами: используйте полиморфизм и рекурсию в своих интересах.
- Открытый/Закрытый принцип . Вы можете вводить в приложение новые типы элементов, не нарушая существующий код, который теперь работает с деревом объектов.
- Возможно, будет сложно предоставить общий интерфейс для классов, функциональность которых слишком сильно различается.
 В некоторых сценариях вам потребуется чрезмерно обобщить интерфейс компонента, что усложнит его понимание.
В некоторых сценариях вам потребуется чрезмерно обобщить интерфейс компонента, что усложнит его понимание.
Вы можете использовать Builder при создании сложных составных деревьев, потому что вы можете запрограммировать его этапы построения для рекурсивной работы.
Chain of Responsibility часто используется в сочетании с Composite. В этом случае, когда листовой компонент получает запрос, он может передать его по цепочке всех родительских компонентов до корня дерева объектов.
Вы можете использовать итераторы для обхода составных деревьев.
Вы можете использовать Visitor для выполнения операции над всем составным деревом.
Вы можете реализовать общие конечные узлы составного дерева как приспособленцы, чтобы сэкономить немного оперативной памяти.
Composite и Decorator имеют схожие структурные диаграммы, поскольку оба полагаются на рекурсивную композицию для организации неограниченного количества объектов.

Decorator подобен Composite , но имеет только один дочерний компонент. Есть еще одно существенное отличие: Decorator добавляет дополнительные обязанности обернутому объекту, а Composite просто «суммирует» результаты своих дочерних элементов.
Однако шаблоны также могут взаимодействовать: вы можете использовать Decorator для расширения поведения определенного объекта в Composite дереве.
Проекты, в которых интенсивно используются Composite и Decorator, часто могут выиграть от использования Prototype. Применение шаблона позволяет клонировать сложные структуры вместо того, чтобы воссоздавать их с нуля.
Построение с помощью шаблонов: древовидный шаблон
Многие из рассмотренных нами ранее шаблонов проектирования схем подчеркивали, что экономия времени на операциях JOIN является преимуществом. Данные, к которым обращаются вместе, должны храниться вместе, и некоторое дублирование данных допустимо. Хорошим примером является шаблон проектирования схемы, такой как расширенная ссылка. Однако что, если данные, которые нужно объединить, являются иерархическими? Например, вы хотите определить цепочку отчетности от сотрудника до генерального директора? MongoDB предоставляет оператор $graphLookup для навигации по данным в виде графиков, и это может быть одним из решений. Однако, если вам нужно выполнить много запросов к этой иерархической структуре данных, вы можете применить то же правило хранения вместе данных, к которым осуществляется доступ вместе. Здесь мы можем использовать шаблон дерева.
Данные, к которым обращаются вместе, должны храниться вместе, и некоторое дублирование данных допустимо. Хорошим примером является шаблон проектирования схемы, такой как расширенная ссылка. Однако что, если данные, которые нужно объединить, являются иерархическими? Например, вы хотите определить цепочку отчетности от сотрудника до генерального директора? MongoDB предоставляет оператор $graphLookup для навигации по данным в виде графиков, и это может быть одним из решений. Однако, если вам нужно выполнить много запросов к этой иерархической структуре данных, вы можете применить то же правило хранения вместе данных, к которым осуществляется доступ вместе. Здесь мы можем использовать шаблон дерева.
Шаблон дерева
Существует множество способов представить дерево в устаревшей табличной базе данных. Наиболее распространенные из них для узла в графе, чтобы перечислить своего родителя и для узла, чтобы перечислить своих дочерних элементов. Оба эти представления могут потребовать множественного доступа для построения цепочки узлов.
В качестве альтернативы мы можем сохранить полный путь от узла к вершине иерархии. В этом случае мы в основном будем хранить «родителей» для каждого узла. В табличной базе данных это, скорее всего, будет сделано путем кодирования списка родителей. Подход в MongoDB состоит в том, чтобы просто представить это как массив.
Как видно здесь, в этом представлении есть некоторое дублирование данных. Если информация относительно статична, как в генеалогии, ваши родители и предки не изменятся, что упрощает управление этим массивом. Однако в нашем примере с корпоративной структурой, когда что-то меняется и происходит реструктуризация, вам нужно будет обновить иерархию по мере необходимости. Это все еще небольшие затраты по сравнению с преимуществами, которые вы можете получить, если не будете все время рассчитывать деревья.
Пример использования
Каталоги товаров — еще один очень хороший пример использования шаблона «Дерево». Часто товары относятся к категориям, которые являются частью других категорий. Например, твердотельный накопитель может находиться в разделе Жесткие диски , который находится в разделе Хранилище , который находится в разделе Компьютерные комплектующие . Иногда организация категорий может меняться, но не слишком часто.
Обратите внимание в документе выше на поле ancestor_categories , которое отслеживает всю иерархию. У нас также есть поле родительская_категория . Дублирование непосредственного родителя в этих двух полях — это передовой метод, который мы разработали после работы со многими клиентами, использующими древовидный шаблон. Включение поля «родительский» часто бывает удобным, особенно если вам нужно поддерживать возможность использования $graphLookup в ваших документах.
Хранение предков в массиве дает возможность создать многоключевой индекс для этих значений.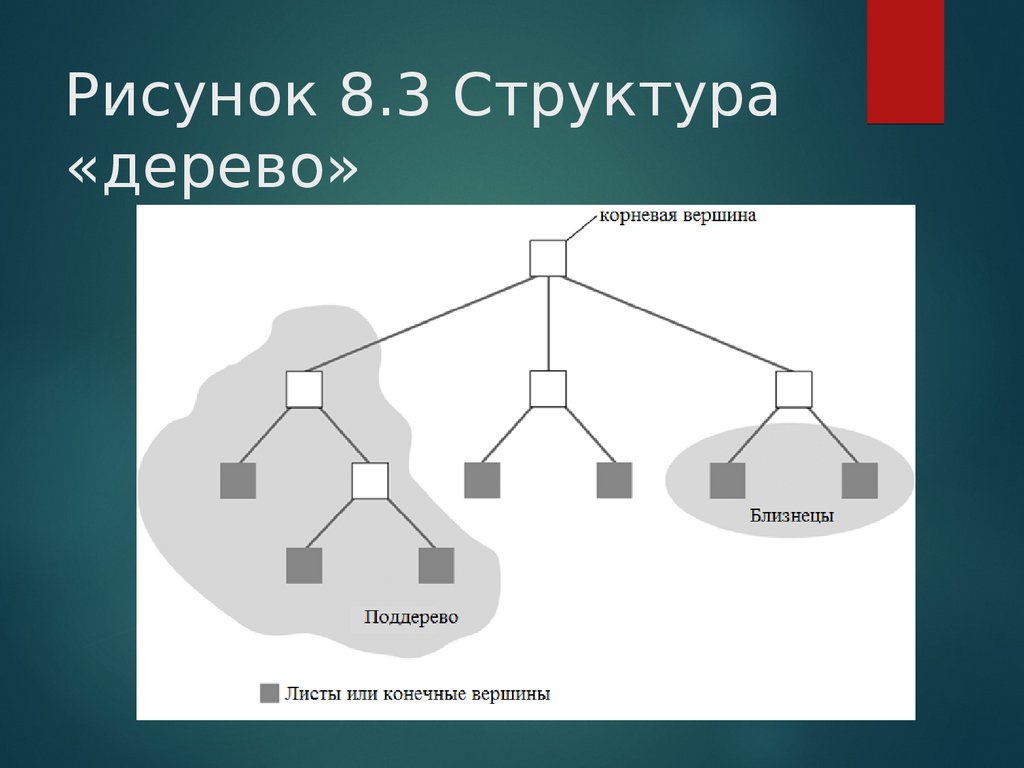


 .. }
метод move(x, y)
это.х += х, это.у += у
метод draw() есть
// Нарисуйте точку в точках X и Y.
// Все классы компонентов могут расширять другие компоненты.
класс Circle extends Dot is
радиус поля
конструктор Circle(x, y, радиус) { ... }
метод draw() есть
// Нарисуйте окружность по X и Y с радиусом R.
// Составной класс представляет сложные компоненты, которые могут
// есть дети. Составные объекты обычно делегируют фактическую
// работаем со своими детьми, а потом "суммируем" результат.
класс CompoundGraphic реализует графику
дочерние поля: массив графических
// Составной объект может добавлять или удалять другие компоненты
// (как простой, так и сложный) в или из его дочернего списка.
метод add(child: Graphic)
// Добавляем дочерний элемент в массив дочерних элементов.
метод удаления (дочерний элемент: графика)
// Удалить дочерний элемент из массива дочерних элементов.
метод move(x, y)
foreach (ребенок в детях) делать
ребенок.
.. }
метод move(x, y)
это.х += х, это.у += у
метод draw() есть
// Нарисуйте точку в точках X и Y.
// Все классы компонентов могут расширять другие компоненты.
класс Circle extends Dot is
радиус поля
конструктор Circle(x, y, радиус) { ... }
метод draw() есть
// Нарисуйте окружность по X и Y с радиусом R.
// Составной класс представляет сложные компоненты, которые могут
// есть дети. Составные объекты обычно делегируют фактическую
// работаем со своими детьми, а потом "суммируем" результат.
класс CompoundGraphic реализует графику
дочерние поля: массив графических
// Составной объект может добавлять или удалять другие компоненты
// (как простой, так и сложный) в или из его дочернего списка.
метод add(child: Graphic)
// Добавляем дочерний элемент в массив дочерних элементов.
метод удаления (дочерний элемент: графика)
// Удалить дочерний элемент из массива дочерних элементов.
метод move(x, y)
foreach (ребенок в детях) делать
ребенок. двигаться (х, у)
// Композит выполняет свою основную логику в конкретном
// путь. Он рекурсивно проходит через всех своих потомков,
// сбор и подведение их итогов. Поскольку
// потомки композита передают эти вызовы своим
// дочерние элементы и т. д., просматривается все дерево объектов
// как результат.
метод draw() есть
// 1. Для каждого дочернего компонента:
// - Нарисовать компонент.
// - Обновить ограничивающий прямоугольник.
// 2. Нарисуйте пунктирный прямоугольник, используя ограничивающий
// координаты.
// Клиентский код работает со всеми компонентами через их базу
// интерфейс. Таким образом, клиентский код может поддерживать простой лист.
// компоненты, а также сложные композиты.
класс ImageEditor
поле все: CompoundGraphic
метод загрузки ()
все = новый CompoundGraphic()
all.add (новая точка (1, 2))
all.add(новый круг(5, 3, 10))
// ...
// Объединение выбранных компонентов в один сложный композит
// составная часть.
двигаться (х, у)
// Композит выполняет свою основную логику в конкретном
// путь. Он рекурсивно проходит через всех своих потомков,
// сбор и подведение их итогов. Поскольку
// потомки композита передают эти вызовы своим
// дочерние элементы и т. д., просматривается все дерево объектов
// как результат.
метод draw() есть
// 1. Для каждого дочернего компонента:
// - Нарисовать компонент.
// - Обновить ограничивающий прямоугольник.
// 2. Нарисуйте пунктирный прямоугольник, используя ограничивающий
// координаты.
// Клиентский код работает со всеми компонентами через их базу
// интерфейс. Таким образом, клиентский код может поддерживать простой лист.
// компоненты, а также сложные композиты.
класс ImageEditor
поле все: CompoundGraphic
метод загрузки ()
все = новый CompoundGraphic()
all.add (новая точка (1, 2))
all.add(новый круг(5, 3, 10))
// ...
// Объединение выбранных компонентов в один сложный композит
// составная часть. метод groupSelected (компоненты: массив графики)
группа = новый CompoundGraphic()
foreach (компонент в компонентах) делать
group.add(компонент)
все.удалить(компонент)
все.добавить(группа)
// Будут отрисованы все компоненты.
все.рисовать()
метод groupSelected (компоненты: массив графики)
группа = новый CompoundGraphic()
foreach (компонент в компонентах) делать
group.add(компонент)
все.удалить(компонент)
все.добавить(группа)
// Будут отрисованы все компоненты.
все.рисовать()

 В некоторых сценариях вам потребуется чрезмерно обобщить интерфейс компонента, что усложнит его понимание.
В некоторых сценариях вам потребуется чрезмерно обобщить интерфейс компонента, что усложнит его понимание.