Соты как нарисовать – Как нарисовать улей для пчел, соты карандашом или красками поэтапно?

Содержание

Проект по геометрии «Геометрия пчелиных сот» – Документ 1 – УчМет

МОУСОШ№2 имени Героя Советского Союза А.В.Ляпидевского гЕйска МО Ейский район.

«Геометрия пчелиных сот»

Выполнила:

Дроздова Яна , ученица 8Б класса

Руководитель:

Бобровникова Т.В.

учитель математики

гЕйск 2012г

Актуальность работы. Умение применять знания школьного курса геометрии в жизни, что способствует расширению кругозора и уделение более пристального внимания школьному материалу.

Цель работы. Для полного раскрытия темы ставится следующая цель: умение решать задачи практического характера, с применением приобретенных знаний в школе; расширение кругозора в ходе исследования, а так же показать связь математики с жизнью и эффективность математики.

Постановка задач. Достижение поставленной цели возможно путем рассмотрения следующих задач: 1) доказательство составления паркета из правильных многоугольников: 2) выявления правильного многоугольника с наименьшим периметром; 3) применение геометрических построений при рассмотрении пчелиных ячеек сот;

4) выявление наименьшей площади поверхности многогранника.

Объект исследования. Объектом изучения работы является пчела, ее соты.

Содержание работы.

— начало исследования – знакомство с интересной задачей про пчел, а так же наблюдение

за строительством пчелиных сот;

— причины, по которым строительство ячеек сот соответствует правильному

шестиугольнику;

— принцип построения паркетов из правильных многоугольников;

— выявление наименьшего периметра правильного многоугольника с применением формул

нахождения площадей, сторон и периметров этих многоугольников;

— построение одной ячейки с применением геометрических построений и знанием

пространственных тел- многогранников.

— сравнение площадей поверхности многогранников и пчелиной ячейки;

— геометрические способности пчел помогают им экономить время, воск и силы.

Выводы по работе.

В заключении мне бы хотелось сказать, что геометрический подход к природным явлениям позволяет увидеть внутренний мир, гармонию, структуру этого явления.

А исследования, проведенные в ходе работы, знакомят и сближают нас с гармонией

и целесообразностью природы.

Оглавление.

1. Вступление.

Связывая природу, математику, и искусство, можно убедиться

в том, что для тех, кто стоял у истоков искусства, природа и

человек были образцами для подражания. Есть такие творения

природы, которых человек порой не замечает___________________стр2.

2. Основная часть.

1) Сеть правильных шестиугольников_______________________стр3.

2) Паркет:

а) формулировка задачи о составлении паркета____________стр3.

б) доказательство задачи_______________________________стр4.

в) составление паркета из правильного треугольника,

квадрата и правильного шестиугольника_______________стр5.

3) Расчетливая геометрия:

а) доказательство того, что периметр правильного

шестиугольника наименьший из периметров

остальных правильных многоугольников ______________стр6.

б) построение ячейки пчелиных сот, и их проекции_________стр8.

в) доказательство того, что площадь поверхности

пчелиной ячейки наименьшая из поверхностей

других многогранников, имеющих одинаковый

объем____________________________________________стр10.

3. Заключение.

Всесторонняя эффективность математики___________________стр11.

4. Список литературы ____________________________________стр12

1. Введение

Пчёлы – удивительные творения природы. Геометрические способности пчёл проявляются при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их рёбрам, то будет видна сеть правильных шестиугольников, уложенных в виде паркета.

Возникает вопрос: «Почему пчёлы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, казалось бы, гораздо проще сконструировать?»

В учебнике за пятый класс есть очень интересная задача о пчёлах. А так как мы сами разводим пчёл, то я решила обратить на неё наиболее пристальное внимание.

Задача №1:

Чтобы собрать 100 грамм мёда, пчела доставляет в улей 16 тысяч нош нектара. Вопрос задачи: какова масса одной ноши?

Решение:

100 : 16000=0,00625 (г) -масса одной ноши.

Ответ: 0,00625 грамм.

А умещает пчела свою ношу на своей ножке в мешочке.

Решив эту задачу, можно сделать следующий вывод: пчела очень трудолюбива, прикладывает огромные усилия для того чтобы, собрать мёд.

Собирая нектар с цветков, пчела «налетает» около трёхсот километров, посетив при этом девятнадцать миллионов цветков. А несколько килограммов мёда – это уже несколько километров. Скорость полёта пчелы – 6,5 километров в час. Продолжительность жизни пчелы 30-35 дней.

2.Основная часть.

Теперь попытаемся ответить на вопрос: «Почему пчелы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов?

Чтобы ответить на этот вопрос, необходимо предварительно выяснить, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пропусков, то есть уложить их в виде паркета.

Выполняя несложные расчёты, убеждаемся, что такими многоугольниками могут быть только квадраты, правильные треугольники и правильные шестиугольники.

Квадрат правильный треугольник правильный шестиугольник.

Задача №2:

Действительно, сумма внутренних углов выпуклого n-угольника равна

(n-2)·180º, где n-число сторон многоугольника. Сумма углов правильных n-угольников, сходящихся в одной вершине паркета, равна 360º. Тогда приравняв сумму внутренних углов к числу 360, мы получим следующее равенство: .

Решаем это уравнение относительно числа к, тогда получим:

или ,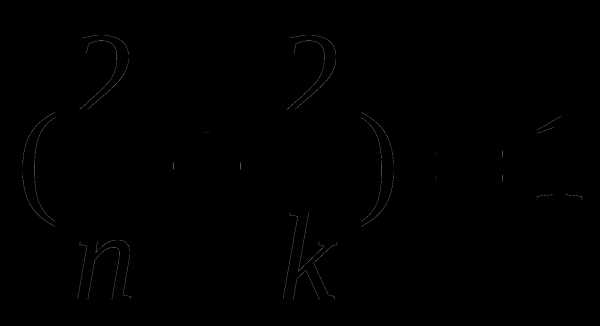

где k — число углов, сходящихся в одной вершине паркета.

Отсюда .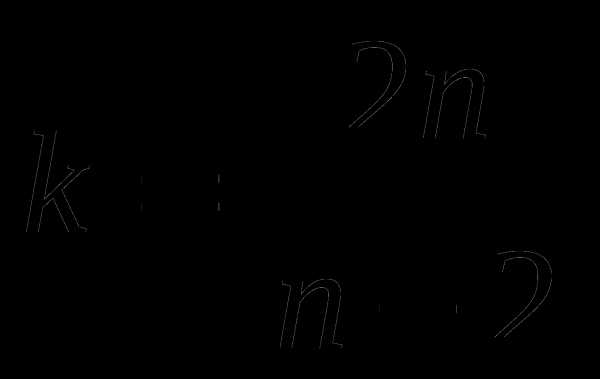

Рассмотрим некоторые правильные многоугольники.

1). Возьмём треугольник с количеством сторон равным трём.

Тогда, если n=3, то k=6. А это значит, что в одной вершине паркета могут сходиться шесть правильных шестиугольников;

2). Возьмём квадрат с количеством сторон равным четырём.

Тогда, если n=4, то k=4, то есть в одной вершине паркета могут сходиться четыре квадрата.

3). Возьмём пятиугольник с количеством сторон равным пяти.

Если n=5, то k=3,3. А так как k получили не целое число, то не существует паркета из правильных пятиугольников.

4). Возьмём шестиугольник с количеством сторон равным шести.

Тогда, если n=6, то k=3, то есть в одной вершине паркета могут сходиться три правильных шестиугольника;

5). Возьмём семиугольник с количеством сторон равным семи.

Если n=7, то k=2,8. А так как k получили не целое число, то не существует паркета из правильных семиугольников. И так можно продолжать дальше.

Теперь рассуждаем следующим образом: 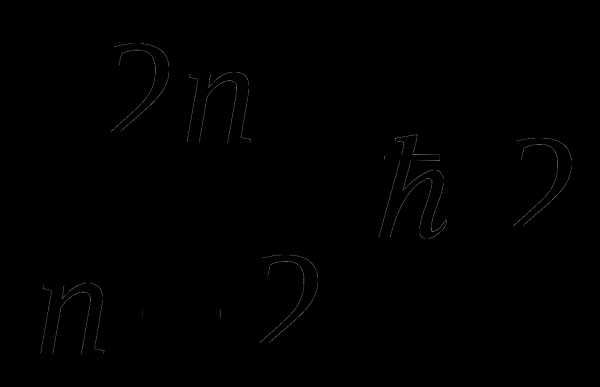,так как внутренний угол правильного многоугольника меньше 180º;

значит,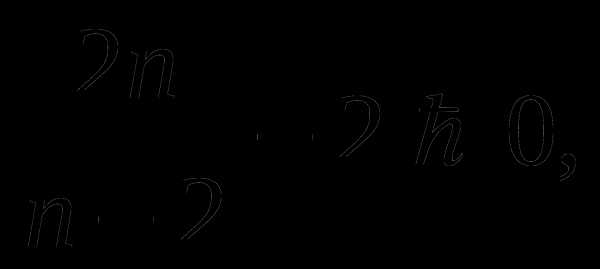

или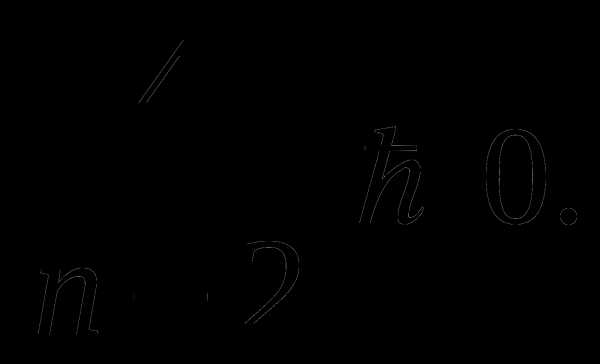

По смыслу задачи значения n, k и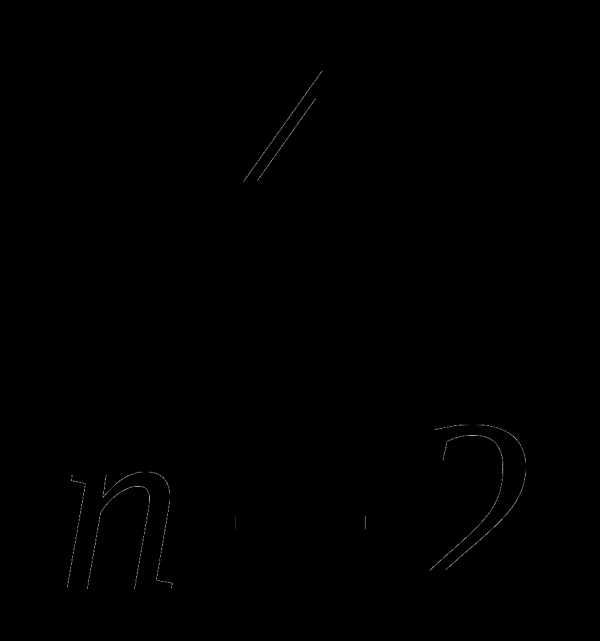

могут быть только целыми , поэтому 4 делится нацело на (n-2). Отсюда n = 3,4,6.

Итак, мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, или квадраты, или правильные шестиугольники. Только ими можно уложить паркет без пропусков.

Паркеты:

1) из правильных треугольников

2) из правильных четырехугольников

3) из правильных шестиугольников

Попробуем дальше развить «пчелиную» тему.

Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, рассмотрим вспомогательную задачу.

Задача №3:

Даны три равновеликие друг другу фигуры – правильный треугольник, квадрат, правильный шестиугольник. Какая из данных фигур имеет наименьший периметр?

Дано: правильный треугольник, квадрат, правильный треугольник. S – из правильных многоугольников. . S=4 см²

Найти: периметр каждого правильного многоугольника.

Решение:

Пусть S – площадь каждой из данных фигур.

а₃, а₄, а₆ — стороны соответствующих многоугольников.

S=4 см².

1). Тогда вычислим площадь треугольника по формуле:

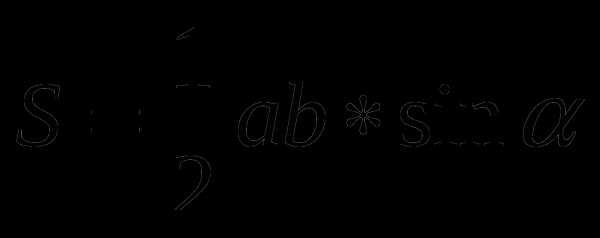
Подставив данные правильного треугольника в эту формулу, получим:

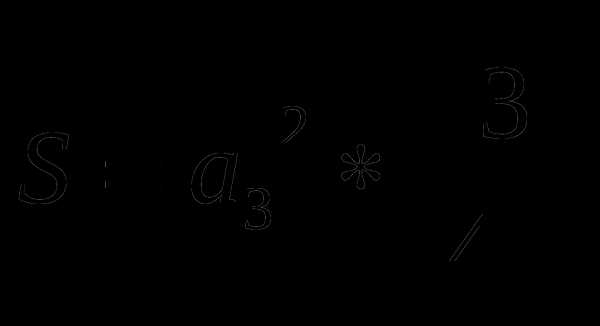
2). Площадь квадрата вычислим по формуле:

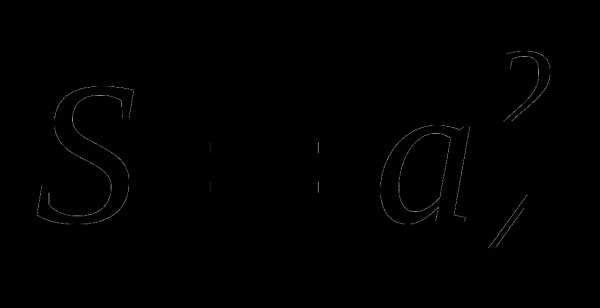
3). Площадь правильного шестиугольника состоит из шести площадей правильного треугольника. Тогда получим:

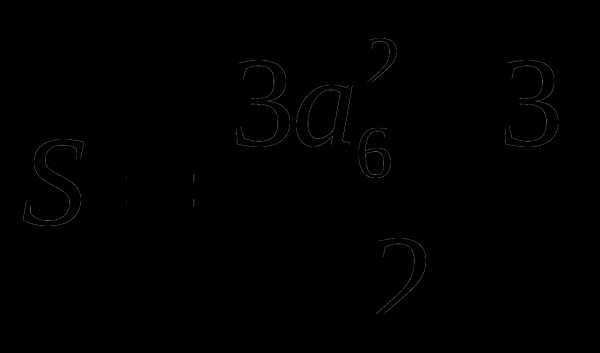
Теперь нетрудно вычислить периметр каждой фигуры, зная её площадь.

Сначала выразим сторону каждого многоугольника через его площадь, затем найдем периметр этого многоугольника:

, тогда .

Подставив в формулу значение площади, равное 4 см², получим, что

Р ≈ 9,1 см.

Аналогично выразим сторону квадрата через его площадь и найдем периметр квадрата при заданном значении его площади:

, тогда , значит

Р = 8 см.

Осталось выразить сторону правильного шестиугольника через его площадь и найти периметр:

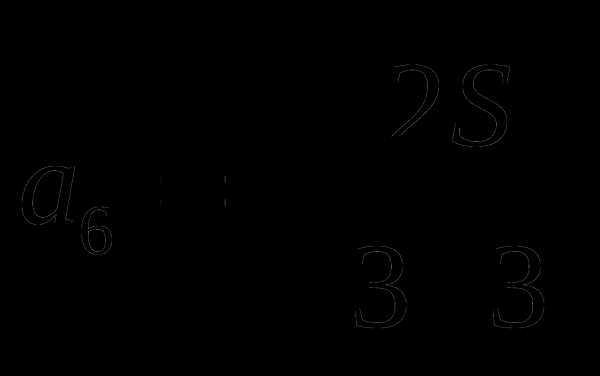, тогда , получим:

Р ≈ 4,6 см.

Для сравнения периметров фигур найдём их отношение:

Мы видим, что из трёх правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, выбрав правильный шестиугольник, мудрые пчёлы экономят воск и время для построения сот.

Надо сказать, что на этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот.

Соты в улье свешиваются сверху вниз наподобие занавесок:

пчёлы прикрепляют их к потолку смесью воска или пчелиного клея (прополиса). Ячейки уложены в пласты и соприкасаются общими донышками.

Но донышки ячеек не плоские, а представляют собой части трёхгранных углов, гранями которых являются равные ромбы.

Рис.2.

Рис. 1.

На рисунке 1 изображена пчелиная ячейка в общем виде, а на рисунке 2 – её проекции: вид сверху, вид спереди и вид сбоку.

Попробуем построить развёртку многогранника (одна ячейка сот). Но прежде чем начать построение сот развёрстки, необходимо рассмотреть чисто геометрически, как получается ячейка.

Сначала построим изображение правильной шестиугольной призмы. Проведём диагонали верхнего основания призмы и на оси призмы возьмём некоторую точку S. Через прямые и точку S проводим три плоскости, которые отсекают от призмы три равные треугольные пирамиды . Получившийся многогранник и является пчелиной ячейкой.

Поскольку боковая поверхность многогранника представляет собой шесть равных между собой трапеций, то для получения развёртки построим эти трапеции. Их размеры возьмём такими же, как на рисунке 2 , причём отрезок MS на рисунке 2, a-это диагональ ромба в верхней части ячейки.

Построим отрезок AA´=AB+BC+CD+DE+EF+FA (рисунок 4). На продолжении ребра CL от точки L отложим отрезок LS и из точки L проведём окружность радиусом, равным, например, отрезку. После этого построим середину отрезка LS, проведём через неё перпендикулярную к нему

Рис. 4.

прямую, которая пересекает дугу окружности в двух вершинах ромба. Два других ромба строим следующим образом: из вершины ромба проводим окружность радиусом, равным стороне построенного ромба, а из вершины S – окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают ещё одну вершину ромба. Остальные построения очень просты. Развёртка пчелиной ячейки показана на рисунке 4.

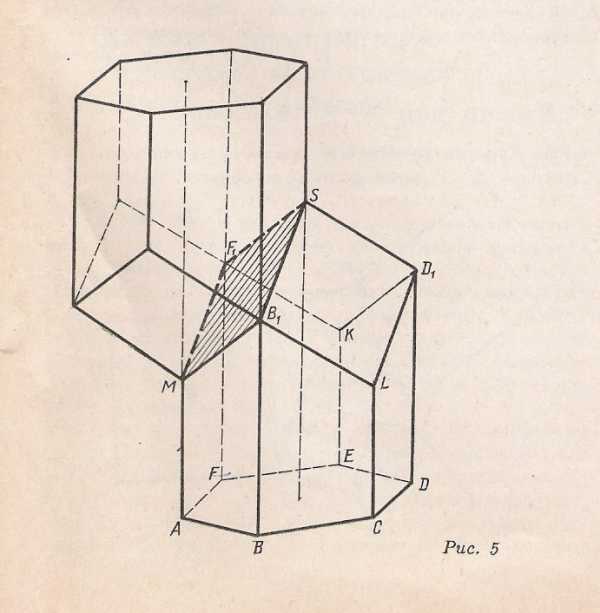
. А на рисунке 5 можно увидеть, как соприкасаются ячейки в улье; их общая часть является ромбом.

Когда говорят о пчёлах, то чаще всего демонстрируют рисунок 6 , показывающий соты в разрезе плоскостью, перпендикулярной боковому ребру и пересекающей все соты по правильным шестиугольникам.

Рис.6.

Если продолжить одну из боковых граней ячейки так, чтобы она пересекала остальные соты, то сечение будет таким, как показано на рисунке 7.

Рис. 7.

Небезынтересен вопрос, почему пчёлы строят донышки своих ячеек в форме части трёхгранного угла, в качестве граней которого служат ромбы. Нельзя ли было поступить проще, сделать дно сот плоским, то есть обычным правильным шестиугольником? Какая же здесь выгода для пчёл?

Вернёмся к ячейке-многограннику на рисунке 3. Объём многогранника

равен объёму правильной шестиугольной призмы. Как нетрудно заметить, объём пирамиды равен утроенному объёму одной из равных пирамид.

Пирамиды и равны (они симметричны относительно точки Т). Мы можем самостоятельно провести доказательство равенства названных пирамид, оно несложно. Итак, объёмы пчелиной ячейки и правильной шестиугольной призмы равны.

Зато площадь ее поверхности меньше площади поверхности шестиугольной призмы.

3. Заключение.

В имеющейся литературе приводятся сведения о том, что благодаря такой «математической» работе расчётливые «геометры» экономят около 2 % воска. Количество воска, сэкономленного при постройке 54 ячеек, может быть использовано для одной такой же ячейки.

В итоге необходимо сказать, что пчелиные соты представляют собой пространственный паркет, поскольку заполняют пространство так, что не остаётся просветов.

Как в заключение не согласиться с мнением Пчелы из сказки «Тысяча и одна ночь»:

«Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».

Так с помощью геометрии и математического анализа мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики.

4. Список литературы:

1) А.И.Азевич «Двадцать уроков гармонии» — гуманитарно – математический

цикл;

2)Журнал: «Математика в школе» №1 1995 г.

3) Журнал: «Пчеловод», подшивка за 2001 год.;

4) Детская энциклопедия: «Что? Где? Почему?»

5) Учебник: «Геометрия 7-11 класс» Погорелов;

6) Учебник: « Математика 5 класс» Виленкин.

www.uchmet.ru

НЕТРАДИЦИОННЫЕ ТЕХНИКИ РИСОВАНИЯ. ПЧЁЛКИ и СОТЫ.

НЕТРАДИЦИОННЫЕ ТЕХНИКИ РИСОВАНИЯ. ПЧЁЛКИ и СОТЫ.

Создание рисунка сот методом оттиска и отпечатка.
Задачи:
Познакомить детей с вариантами использования нетрадиционных техник рисования.
Продолжать совершенствовать умения работать с гуашью.
Закреплять умение создавать декоративный рисунок.
Развивать воображение.
Развивать мелкую моторику
Воспитывать аккуратность при выполнении рисунка
Воспитывать уважительное отношение к насекомым-пчелам.

Пчелиные соты — восковые постройки пчёл, предназначенные для хранения запасов мёда и выращивания потомства; являются также гнездом пчелиной семьи. Пчелиные соты состоят из шестиугольных призматических ячеек, расположенных по обе стороны от общего средостения, которое может быть искусственным
Шестиугольная форма является наиболее экономичной и эффективной фигурой для строительства сот.
Пчелиные соты — наиболее совершенные постройки насекомых. Соты строятся с двух сторон, и способ «крепления» каждой из ячеек не предусматривает каких-либо зазоров и нестыковок во всех трёх измерениях.

Сейчас я хочу представить вашему вниманию мастер класс по изображению сот с пчелами.
Материалы:
1. Альбом(лист формата А4) для рисования
2. Гуашь
3. Губка
5. Палитра или блюдце
6. Кисти №1 , №2 и №4
7. Целлофан с пупырышками
8. Вода
9. Салфетка тканевая

Целлофан с пупырышками бывает разный. Есть такой, в котором обе стороны гладкие , а пупырышки внутри. Он не подойдет. В работе я использовала целлофан , у которого одна сторона гладкая, а другая с пупырышками. Вот на фото я изогнула его ,чтоб видно было. Такой я нашла в упаковке от пластмассовой подставки для зубочисток.Пупырышки должны быть целыми.
Ход работы:
1.Разведем при помощи широкой кисти гуашь на блюдце. В моем первом варианте два вида рисунка. Сначала покажу один из них. Для него нужна гуашь бледно желтого цвета(смешиваем желтую ,белую гуашь и воду) . Наносим гуашь при помощи губки на альбомный лист . Стараемся нанести равномерно и без нажима .Даем подсохнуть.
2.Покрываем пупырчатую сторону целлофана губкой оранжевой, желтой или красной гуашью (я не разводила ее водой, т.к. она у меня достаточно жидкая). Стараемся это сделать достаточно быстро , чтобы гуашь не высохла. Припечатываем на подкрашенный лист (аккуратно, без сдвигов). Проглаживаем при помощи салфетки. Нам нужно получить хороший отпечаток. Вот такие соты у нас получились.
3. Теперь нам не хватает пчел. Какие же соты без пчел? Берем кисточку любого размера и рисуем полуовалы. Так же можно взять ластик и покрыть штамп желтой гуашью при помощи широкой кисти. Делаем оттиски в нескольких местах ,каждый раз прокрашивая штамп.
4. Кистью №2 белой гуашью примакиванием рисуем крылышки. Нужно просто приложить кисть к бумаге горизонтально. Если мы рисуем пчелу летающую, нарисуем ей 4 крыла. Если пчела ходит по сотам ,то 2 крыла и они чуть длиннее (показываем, что она сложила 4).
5. Тонкой кистью №1 прорисовываем каждой пчеле чёрной гуашью мелкие детали ( полоски ,ножки, жало).У летающих пчел ножки не прорисовываем (они поджаты снизу во время полёта).
Рисунок готов! Можно вставить в рамку.

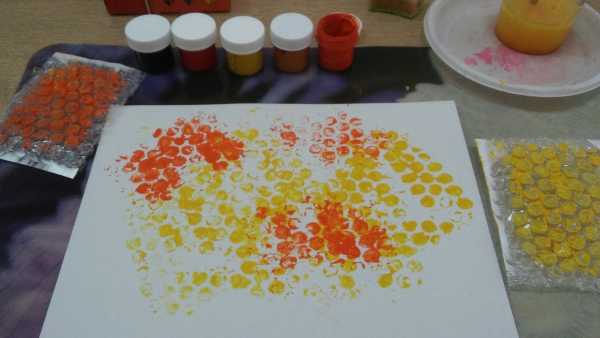
infourok.ru

Как нарисовать мёд акварелью: мастер-класс с фото

Пчелиный мед кроме своих вкусовых качеств, славится еще и уникальными полезными свойствами. О целебных свойствах продукта знали еще в древности, поэтому люди уже на протяжении многих веков занимаются пчеловодством. Мед широко используется не только в кулинарии и пищевой, но в косметологической промышленности тоже. Ведь продукт считается настоящим эликсиром молодости. И сегодняшний урок мы посвятим рисованию этого полезного лакомства. Чтобы сделать сюжет интересным и уникальным мы изобразим два кусочка пчелиных сот и ложку с красивыми медовыми потеками. Рядышком нарисуем маленькую полосатую труженицу – пчелу. Ознакомьтесь со списком инструментов и переходите к созданию рисунка.

Чтобы нарисовать мед акварелью понадобятся следующие инструменты:

бумага для рисования акварелью;
палетка акварельных красок;
палитра;
простой карандаш;
ластик;
колонковые или синтетические мягкие кисти № 4 и 3;
ножницы;
планшет и тонкий скотч;
емкость с водой.

Этапы рисунка

Шаг 1. Начнем, пожалуй, с создания наброска. Грубыми линиями намечаем в нижней части листа кусочки сот. Рядом дорисовываем медовые потеки. Над сотами рисуем ложку с медом. Сплющенным овалом обозначаем пчелу.

Постепенно вырисовываем более четкий и детальный набросок. Вспомогательные штрихи удаляем мягким ластиком.

Набросок рисунка готов. Прикрепляем края бумаги к планшету с помощью двух полос скотча. Таким образом, мы защитим бумагу от деформации.

Шаг 2. Подмалевок медового оттенка создаем с помощью кадмия желтого среднего. Прописываем полупрозрачным цветом ломтики сот, потеки и ложку. Насыщенными мазками оттеняем поверхность нижнего кусочка.

Шаг 3. Сиеной жженой прорабатываем деревянную текстуру ложки.

Шаг 4. Далее маленькой кистью выделяем мелкие ямки сот. Для этого замешиваем из сиены натуральной и золотистой теплый оттенок, и прорабатываем им все выделенные в наброске углубления. После чего смываем с кисти насыщенную краску и оставшимся легким тоном прорисовываем боковые части сот и лужицы меда.

Шаг 5. Кадмием желтым насыщаем базовый тон меда. При обработке не забываем оставлять блики, которые помогут правильно и реалистично передать глянцевую текстуру меда.

Шаг 6. Теперь насыщаем базовый цвет деревянной ложки с помощью сиены жженой. Этим же оттенком немного выделяем затененные участки в сотах.

Шаг 7. А пока слои краски подсыхают, прорисуем пчелу. Нейтрально-черным цветом заполняем контур лапок, крыльев и тельце. Оттеняем крошечные детали бледно-желтой акварелью.

Шаг 8. Далее в смесь из сиены и золотистой акварели добавляем небольшое количество окиси хрома. Проходимся этим тоном по затененным участкам рисунка. Оттеняем зеленоватые мазки бледно умброй жженой.

Шаг 9. Насыщаем контур и тени жженой умброй и нейтрально-черной. Сепией создаем падающую тень.

Шаг 10. Дополняем рисунок синими и желтыми брызгами. Выделяем самые яркие блики белой акварелью.

Рисунок готов. Осталось только дождаться полного высыхания бумаги и снять рисунок с планшета.

Фото:onwomen.ru

onwomen.ru

Модная тенденция — соты

Сегодня мы поговорим и проиллюстрируем такую набирающую обороты в скрап-мире форму, как шестиугольник или соты.
Все чаще и чаще встречаются работы, выполненные с этим узором.

Среди всего разнообразия скрап-материалов соты можно встретить и в виде рисунка на бумаге, и в виде чипборда, дырокола, наклеек, натирок, масок, оверлея и пр.

источник

поизводитель

Разнообразие мотивов и узоров скрап-бумаги с элементами сот позволяет создать различные неповторимые работы.
В скрап-работах можно встретить использование узора соты как в качестве основного фона

источник

А так же и в качестве декоративного дополняющего элемента

источник

Прекрасно смотрится узор соты в виде вырезанного шестиугольника, дополняющего скрап-работу

источник

Придать воздушность работе можно за счет вырезания не только внешней части соты, но внутренней

источник

Техника вырезания и в т.ч. этого узора позволяет создать уникальную двухслойную работу

источник

За отсутствием бумаги с таким узором, можно просто нарисовать на фоновом или дополняющем листе узор соты

источник

Этот узор можно сочетать с другими геометрическими фигурами, например, кругами

источник

Прием наслоения одной вырезанной фигуры соты на другую позволяет добавить объема работе и подчеркнуть отдельные элементы страницы

источник

Специально для этого обзоры я подготовила мини-альбом об одном замечательном событии маленькой девочки
Материалы:
Лист скрапбумаги My Mind’s Eye — Be AmazingHoney Blue
Лист скрапбумаги My Mind’s Eye — Be AmazingSociet
Лист скрапбумаги My Mind’s Eye — Be HappyHoney Pink
Лист картона Ivory, цвет слоновая кость
Лента Seam Binding Blue Jay
Брадсы Dovecraft — Jewel Brads – Blue and Turqoise
Шебби-лента SILKY/CRUSH, цвет GOLD
Набор карточек для журналинга Websters Pages — Journaling Cards — Yacht Club
Пудра для эмбоссинга Wow Primary Lemon — Regular
Бабочки из веллума с рисунком Jenni Bowlin Vellum Embellished Butterflies — Blue