Тень конуса: «Как изобразить тень конуса круг 1 класс?» – Яндекс.Кью

Тени в ортогональных проекциях — презентация онлайн

Тени в ортогональных проекциях
ТЕНИ
Рельефность «происходит от теней и
светов или, другими словами, от
светлого и темного.
Итак, кто избегает теней, избегает
славы искусства»
Леонардо Да Винчи
(Leonardo Da Vinci)
(1452-1519)
Форма предмета воспринимается
точнее, когда предмет освещен и
на его поверхности образуется
светотень
Изображение светотени на проекционных чертежах состоит
из двух графических операций:
— «геометрия теней»;
— «изображение светотени» («отмывка»)
Характер светотени зависит от положения предмета
относительно источника света
и направления лучей к поверхности
«геометрия теней» — это
определение границ (контуров)
собственных и падающих теней,
основанное на построении линии
прикосновения лучевой
поверхности с данной
поверхностью и определение
линии пересечения поверхностей
«изображение светотени» («отмывка»)- графические приемы
выявления светотени на изображении так, чтобы ее
восприятие наиболее близко подходило к восприятию в
натуре. Эта операция основана на физиологии зрительного
восприятия, т.е. на «воздушной перспективе»
4
ВОЗДУШНАЯ ПЕРСПЕКТИВА
Чем освещенное место ближе
к зрителю, тем оно кажется
светлее и ярче, а чем дальше
– тем бледнее и мягче
Светотеневой контраст
(различие между освещенной
и теневой частью
предмета) по мере удаления
от зрителя погашается,
делается менее резким

6. Тени при искусственном освещении

При освещении одной
светящейся точкой лучевая
поверхность будет конической
s
3
2
1
1Т
3Т
2Т
Тени могут быть построены при
искусственном освещении объекта
При искусственном освещении
источник света расположен на
незначительном расстоянии
Лучи света образуют при этом конический
пучок лучей — связку прямых, центром
которой является источник света S
6

7. Тени при естественном освещении

При освещении
параллельными лучами
лучевая поверхность будет
цилиндрической
В
A
BT
CT
b
c
S
C
AT
При естественном освещении источник света
удален в бесконечность и световые лучи
параллельны друг другу
Граница (линия) на поверхности предмета,
разделяющая освещенную часть от находящейся в
тени, называется контуром собственной тени
Контур собственной тени представляет собой
линию касания обертывающей лучевой
поверхности к поверхности предмета
Падающие тени
Тень, полученная от одного предмета на другой или от
одной части поверхности на другую ее часть ,
называется падающей тенью
А линия, ее ограничивающая, – границей или
контуром падающей тени
Граница падающей тени является тенью от границы
собственной тени
На проекционных чертежах (эпюрах) действие воздушной среды не
учитывается, однако зону собственной тени принято показывать
светлее падающей тени, что соответствует действительным условиям

9.

Направление световых лучей a2
A
a3
b3
35о
45о
S3
S2
45о
45о
45о
a1
a2
a3
B b
2
x
b3
b2
b1
45о
b1
S1
a1
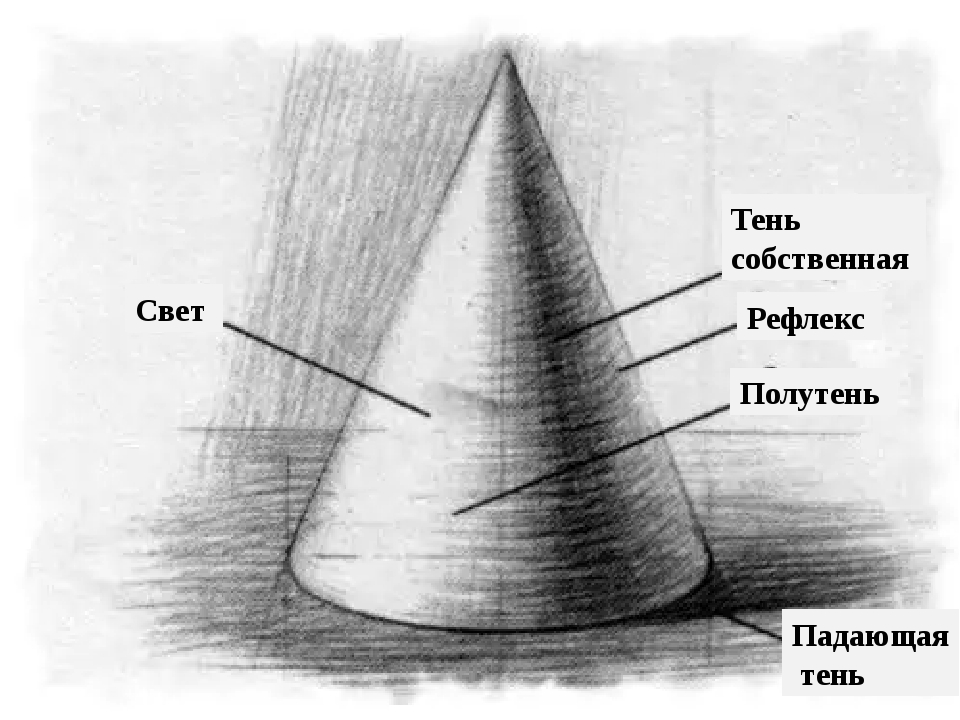
При построении теней на комплексных чертежах освещение считают солнечным, с
параллельными лучами
Источник света считают расположенным слева сверху сзади:
направление лучей света принимают параллельным диагонали куба, грани которого
совмещены с плоскостями проекций
Проекциями диагонали куба являются диагонали квадратов,
т. е. горизонтальная и фронтальная проекции светового луча составляют с осью проекции
х угол 45°, истинный угол наклона луча к плоскости проекций ~ 35°
Такое «стандартное» направление световых лучей создает преимущества при построении
теней и выполнении чертежа:
1) достигаются постоянство и простота построения проекций лучей и теней на чертежах
фасада и плана объекта;
2) облегчаются чтение чертежа и понимание форм, пропорций и размеров элементов
изображенного объекта.
9
a2
z
a2
a3
A
a3
b3
B b
2
b3
x
45о
b2
45о
b1
b1
45о
a1
S2
45о
45о
35о
S3
S1
a1
y
3
2
1
35о
45о
4
45о
5
0,7(0,707)
0,3(0,293)
Диагональ квадрата 1-3 совмещается с его стороной 1-4 и полученная точка 5
соединяется с точкой 2.
Линия 2-5 дает истинный угол наклона диагонали куба (35016I16II).
При построении теней часто приходится делить отрезок прямой в отношении
величин стороны квадрата к его диагонали

11. Построение падающей тени от точки

A
• Позиционная задача на
A2
пересечение прямой с
плоскостью
B2
Aт2
• Тенью, падающей от точки
B
x
A1
на плоскость проекций,
является соответствующий
след луча света,
проходящего через данную
точку
Bт1
B1
А2
В2
Ат2
45о
45о
Вт1
11
А1
В1
Задача
Построить тень от точек
A2
В2
A1
В1
12

13.

Построение падающей тени от точки A
• Позиционная задача на
A2
пересечение прямой с
плоскостью
Aт2
Aт1
A1
A2
Ст2
A1
13
(Aт1)
• Тенью, падающей от точки
на плоскость проекций,
является соответствующий
след луча света,
проходящего через данную
точку

14. Способ выноса

УА
А2
А2
А0
УА
Ат2
45о
А
У
45о
А1
•АА
1
Х1,2 =
АХ1,2
Ат2
А1
УА
У А – удаление точки А от фронтальной плоскости
проекций
14

15. Тени от прямых частного положения

А2
h3
S2
//
В2
• Тень, падающая на
//
Вт1
S1
Ат1
А1
15
h2
В1
плоскость проекций от
отрезка прямой,
параллельного этой
плоскости проекций, равна и
параллельна этому отрезку

16. Тени от прямых частного положения

А2 ≡В2 ≡Вт2
В2
S2
В1
А2
S1
Вт1
А1 ≡В1 ≡Ат1
16
А1
• Тень, падающая на
Ат2
плоскость проекций от
отрезка прямой,
перпендикулярного этой
плоскости проекций,
совпадает с направлением
проекции светового луча на
эту плоскость проекций.

17. Тень от прямой, расположенной под углом 450 к плоскости

y
y
h3
В1 – ВХ = у,
у – вынос
В2
//
y
А2
S2
Вт2
А1
//
45о
y
S1
ВХ
h2
В1
Тень, от горизонтальной
прямой, расположенной
под углом 450 к
фронтальной плоскости
проекций, на этой
плоскости получается с
уклоном 1:2

На данном примере дано
понятие выноса.
Применяется для построения теней поверхностей вращения с осью, занимающей
проецирующее положение и когда можно установить вынос характерных точек
границы собственной тени от плоскости, на которую падает тень.
Удаление В1-ВХ =у, у- вынос точки В относительно фронтальной плоскости.
Ширина тени равна «выносу» линии
17

18. Тени от прямых частного положения

РП2
А2
В2 ≡Вт2
S2
Ат2
45о
S1
А1
РП1
18
В1
Тень от отрезка (общего
положения), лежащего
в вертикальной лучевой
плоскости, совпадает со
следом этой плоскости,
следовательно на фасаде
будет расположена
вертикально.

19. Тени от прямых общего положения

В2
А2
45о
45о
Вт1
Ат1
В1
А1
19

20. Задача: Построить тень от отрезка

А2
В2
45о
45о
В1
А1
20

21. Тени от прямых общего положения

В2
С2
Вт2
А2
A2
A
Ст1
B2
Aт2
B
A1
21
B1
Ат1
(Aт1)
Bт1
Ст2
В1
С1
А1
(Вт1)

22. Задача: Построить тень от отрезка

В2
А2
45о
45о
В1
А1
22

23. Тень от плоскости частного положения

Тень от плоской фигуры на
плоскость, ей параллельную,
изображается фигурой
равной и одинаково
расположенной с исходной
Вт2 фигурой
А2
Ат2
В2
С2
S2
Ст2
S1
23
А1
С1
В1

24. Тень от плоскости частного положения

А2
РП2
В2
Вт2
Ат2
С2
S2
Ст2
45о
S1
С1
А1
РП1
24
В1
Тень от плоской фигуры
(общего положения),
лежащей в вертикальной
лучевой плоскости,
вырождается в отрезок
прямой (как совпадающий
с проецирующей
плоскостью).

25. Тень от плоскости общего положения

С2
В2
S2
Ст2
А2
(Ст1)
45о
45о
Вт1
S1
С1
Ат1
В1
А1
25
Задача: Построить тень от плоскости
С2
В2
S2
А2
45о
45о
S1
С1
В1
А1
26

27. Способ выноса

УА
А0
А2
у
у
УА
45о
АХ1,2
3I
4I
5I
А
• АА
Х1,2 =
2т
3т
УА
У А – удаление точки А от
фронтальной плоскости
проекций
27
2I
4т
А1
1
1I
У
45о
Ат2
• Тень о горизонтальной
полуокружности
• 2 – бликовая точка
• 3 – имеющая максимальный
вынос – фронтальная точка
• 4 – теневая точка

28. Тень от окружности частного положения

О2
d2
c2
I
8т 7 7т
6т
5т
1т
2т
d
8
c
7
6
5
1
2
a
28
aI
4
3
b
4т
3т
Окружность занимает
горизонтальное положение
Тень от окружности строится
на фронтальную плоскость
по характерным точкам
Вписываем окружность в
квадрат
Строим тень от квадрата.
Характерные точки
окружности: на диаметре и
bI на диагоналях
Тень точек на диагоналях
находятся из отношения
стороны квадрата к
диагонали =0,707
Задача: Построить тень от окружности
d2
х
29
О2
c2

30. Тень от точки на поверхность

А
Р
Для построения падающей
тени от точки на плоскость или
поверхность следует через
точку провести световой луч и
построить точку пересечения
его с плоскостью или
поверхностью.
Ат
а
30
Так как световой луч является
прямой линией, то
построение тени точки
сводится к построению
точки пересечения прямой с
плоскостью или
поверхностью

31. Тень от точки на плоскость общего положения

F2
B2
S2
45о
С2
A2т
A2
12
45о
S1
22
D2
B1
A1
21
A1т
11
Q1
F1
31
D1
C1
Построение проекций
падающей тени от
точки Е на плоскость
общего положения,
заданную
четырехугольником
АВСД

32.

Задача: Построить тень от точки на плоскость F2
B2
С2
S2
45о
A2
45о
S1
A1
D2
B1
D1
F1
32
C1

33. Тень от прямой на плоскость общего положения

B2
Тень от прямой на
плоскости П1 и
плоскость общего
положения 1, 2, 3
22
B2т
S2
45о
32
12
A2
21
45о
S1
11
B1т*
B1т
A1
B1
33
P1
31

34. Построение тени параллелепипеда

• Построение собственной и падающей
теней параллелепипеда сводится к
определению собственных и падающих
теней граней − плоских геометрических
объектов.
• В собственной тени находятся две грани
параллелепипеда АВЛК и ВСЛМ. Поэтому
падающей тенью параллелепипеда будет
совокупность падающих теней этих
граней.
• Грани АВЛК и ВСЛМ являются
прямоугольниками частного положения
относительно плоскостей проекций,
поэтому для построения их теней могут
быть использованы известные приемы
построения теней плоских фигур частного
положения.
34

35. Построение тени параллелепипеда на эпюре

35

36. Построение тени пирамиды

36
Построение собственной и
падающей теней пирамиды сводится
к определению собственных и
падающих теней граней − плоских
геометрических объектов.
В собственной тени находится одна
грань пирамиды АВД. Поэтому
падающей тенью параллелепипеда
будет падающая тень этой грани.
Грань является
треугольником общего положения
относительно плоскостей проекций.
Сторона ВД лежит на горизонтальной плоскости проекций, т.е.
совпадает со своей тенью.
Для нахождения теней отрезков АВ и АД требуется построить
падающую действительную и мнимую тени точки А.

37. Построение тени пирамиды на эпюре

37

38. Построение тени цилиндра

38
Для определения контура собственной
тени прямого кругового конуса
проведем две горизонтально
проецирующие лучевые плоскости,
касательные к поверхности цилиндра
и составляющие с фронтальной
плоскостью проекций угол 45о.
Образующие АВ и СД, по которым
плоскости касаются цилиндра, и
полуокружности верхнего и нижнего
оснований определяют контур
собственной тени.
Падающая тень цилиндра ограничена
тенью от контура собственной тени.
Тени от образующих строятся как тени вертикальных прямых.
Нижняя полуокружность совпадает с основанием цилиндра и
расположена на горизонтальной плоскости.
Верхняя полуокружность строится как тень от сектора
окружности, параллельной горизонтальной плоскости.

39. Построение тени цилиндра на эпюре

39
Задача: Построить тени цилиндра
S2

41. Построение тени цилиндра на эпюре без второй проекции

41
ТЕНИ ЦИЛИНДРА
12I
Тени строятся на
фронтальную
плоскость, проходящую
через ось цилиндра
ГСТ
ГПТ
ГСТ – граница
собственной тени
22
32
2т2
ГПТ – граница падающей
тени
12
1т2
3т2
Точки 1I и 2I определяют
положение образующих
цилиндра. 2I- невидимая
ТЕНИ КОНУСА

44. Построение тени конуса

44
Построение собственной и
падающей теней прямого
кругового конуса, основание
которого расположено в
горизонтальной плоскости,
выполняется в следующей
последовательности:
1. Определяем действительную
или мнимую тень от вершины А
на горизонтальную плоскость
проекций.
2. Из горизонтальной проекции полученной тени проводим две
прямые, касательные к окружности основания конуса. Точки
касания этих прямых к окружности основания конуса определяют
положение образующих конуса, которые являются контуром
собственной тени конуса.
3. Меньшая дуга окружности основания конуса и построенные
образующие определяют контур падающей тени.

45. Построение тени конуса на эпюре

45
S2
Задача: Построить тени конуса
S1
S2
ТЕНЬ КОНУСА
с углом наклона образующей к основанию
равным 45О

48. Тень конуса с наклоном образующей 45°

У конуса с наклоном образующей 45°
фронтальная проекция луча совпадает с
очерковой образующей.
S2
22
12
21
S1т
S1
11
Собственная тень занимает одну
четверть поверхности нижней полы конуса и
три четверти поверхности верхней полы.
Теневыми образующими являются
очерковая: правая фронтальная (S1) и
профильная невидимая (S2).
У обратного – левая фронтальная и
видимая профильная.
Границей собственной тени у
прямого 45о конуса являются
образующие: правая
фронтальная (S1) и профильная
невидимая (S2)
48
Касательным конусом с образующей под
45о будут определяться точки границы
собственной тени на фронтальном и
профильном очерках поверхности
вращения.

49. Тень конуса с наклоном образующей 45°

О2 ≡42
S2
3т1
Границей собственной тени у
обратного конуса – левая
фронтальная и видимая
профильная
От1
S1т
4т1
31
49
S1
41
Касательным конусом с образующей
под 45о будут определяться точки
границы собственной тени на
фронтальном и профильном
очерках поверхности вращения

51.

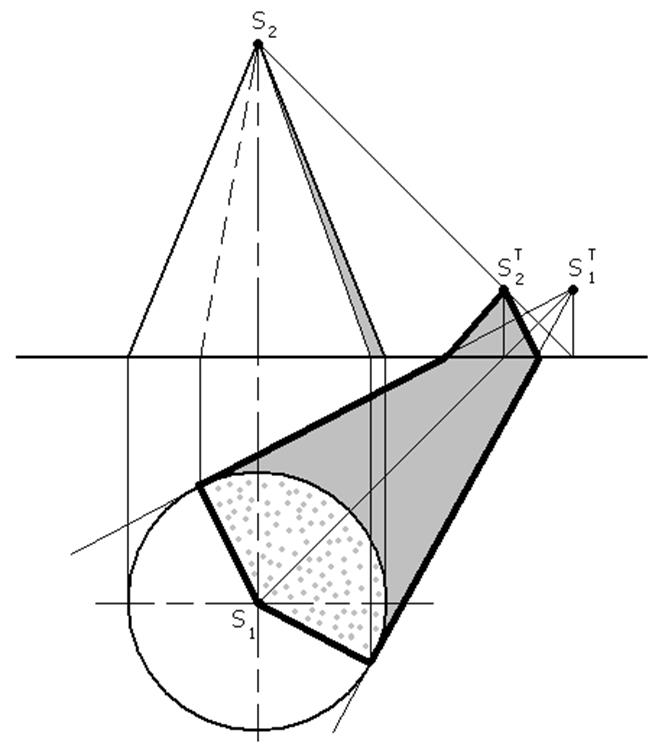Тень конуса с наклоном образующей 35° У конуса с наклоном
образующей 35° контуром тени
может служить единственная
образующая, которая на фасаде
имеет наклон 45°.
S2
S2т
S1т
S1
51
Поверхность нижней полы
конуса будет вся освещена, а
поверхность верхней полы
конуса — вся в тени.
Касательным конусом
с образующей под 35о будут
определяться высшая и низшая
точки границы собственной тени
на поверхности вращения

52. Собственные тени вспомогательных конусов общего вида

S2
1 способ
Е2
12
22
S1т Затем радиусом S Е
1 1
Е1
21
S1
52
Для более точного
определения точек
касания 1и 2 находят
точку Е- середину
горизонтальной проекции
луча S1S1т.
11
делают засечки на
окружности и определяют
точки 1 и 2

53. Собственные тени вспомогательных конусов общего вида

S2
2 способ
Е2
22
22
12
12
Е2
S2
53

54.

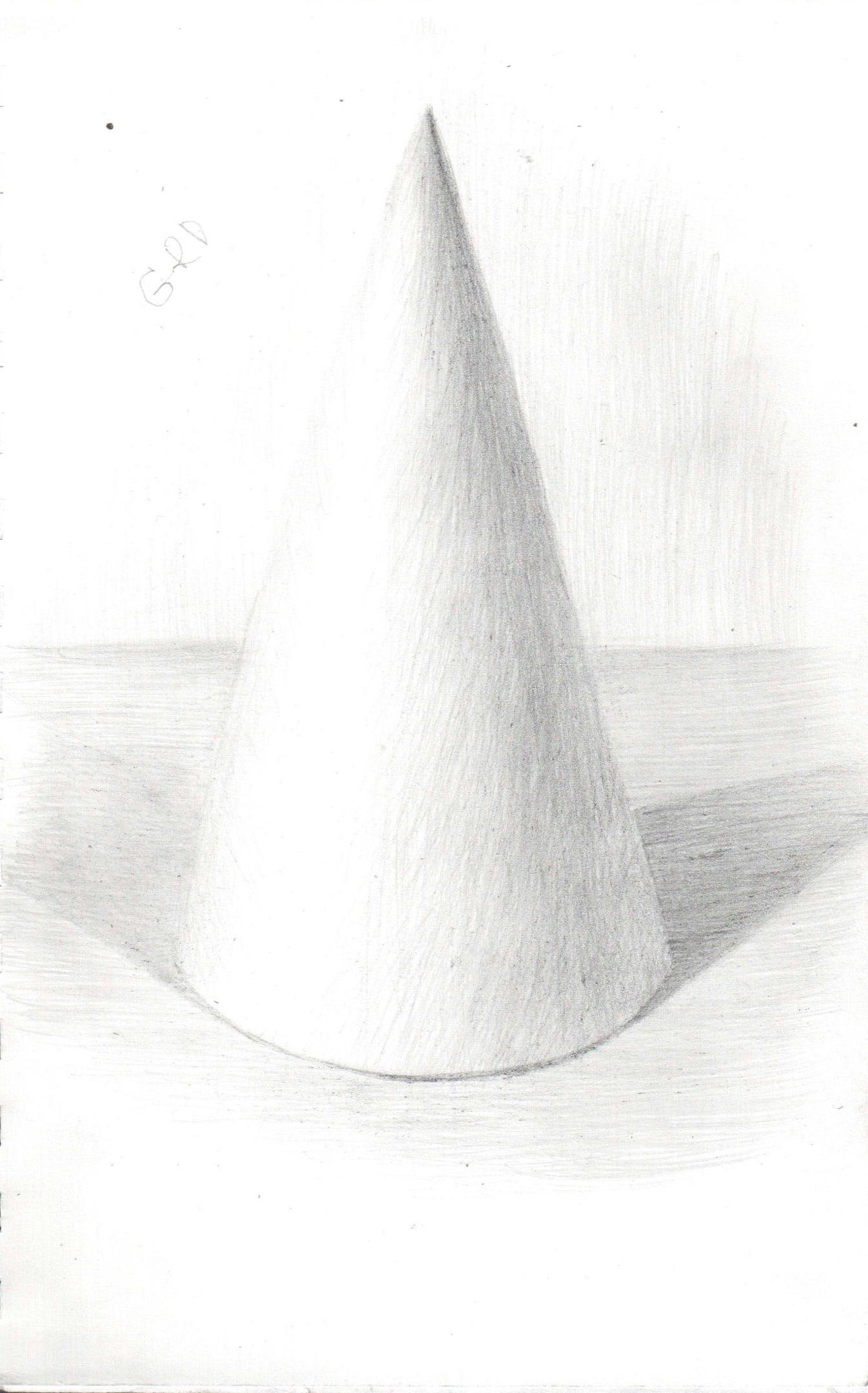Собственные тени вспомогательных конусов общего вида 3 способ
S2
Ат2 А2
12 22
1т2
54
Тени строятся на фронтальную
плоскость, проходящую через ось конуса.
Из точки тени от вершины конуса
проводится касательная к тени основания.
«Обратным» лучом из точки 4т2 находим
точку 42 и образующую S242, которая
будет являться контуром собственной
тени и Sт24т23т22т21т2Aт2- контур
падающей тени
К совмещенной с фасадом окружности
основания проводят горизонтальную
32
В2 Вт2 касательную до точки пересечения с
продолжением очерковой образующей. Из
42
4т2
полученной точки проводят луч под углом
3т2 в 45о, которая пересекаясь с
окружностью, дает необходимые точки 11
2т2
и 21 .
Их проекции 12 и 22 определят положение
границы собственной тени

55. Собственные тени вспомогательных конусов общего вида

3 способ
S2
N2
21
11
12
22
22
12
11
21
N2
S2
55

56.

Построение тени конуса на эпюре без второй проекции
56
Для определения тени на конусе нужно
построить к его фронтальной проекции
половину горизонтальной проекции.
Из точки 1 полуокружности проведем
прямую 1–2 параллельно проекции левой
очерковой образующей конуса до
пересечения с горизонтальным диаметром
в точке 2.
Через точку 2 построим прямую под углом
45° к диаметру, и отметим точку 3
пересечения прямой с окружностью.
Проведем через точку 3 вертикальную
прямую, найдем точку 4, через которую
проходит видимая граница собственной
тени конуса.
Если провести через точку 2 прямую 2–5
также под углом 45° к диаметру, а через
точку 5 – вертикальную прямую, то получим
точку 6, через которую проходит невидимая
граница собственной тени.

57. Построение собственной тени сферы

• Тень на шаре строится в такой
57
последовательности: проведем
вертикальный, горизонтальный и два
наклонных под углом 45° диаметра
окружности – фронтальной проекции
шара.
Через точку 1 наклонного диаметра 1–2
проведем горизонтальную и
вертикальную прямые, а также прямые,
наклоненные под углом 30° к диаметру
1–2.
В пересечении прямых с
соответствующими диаметрами получим
точки 3, 4, 7, 8.
Точки 5 и 6 получены в результате
проведения вертикальной и
горизонтальной прямых через точку 2.
Соединив плавной кривой построенные
точки, получим эллипс – фронтальную
проекцию границы собственной тени
шара (половина эллипса невидима).

58. Построение падающей тени сферы

58
Для построения падающей
тени от сферы применяем
метод замены плоскостей
проекций

59. Способ обратных лучей

Тени на ступенях лестницы
Тенеобразующими ребрами боковой стенки являются вертикальное,
наклонное и горизонтальное ребра.
Вертикальное ребро повторяет профиль лестницы до точки а0.
Тень от горизонтального ребра совпадает с проекцией луча.
59

60.

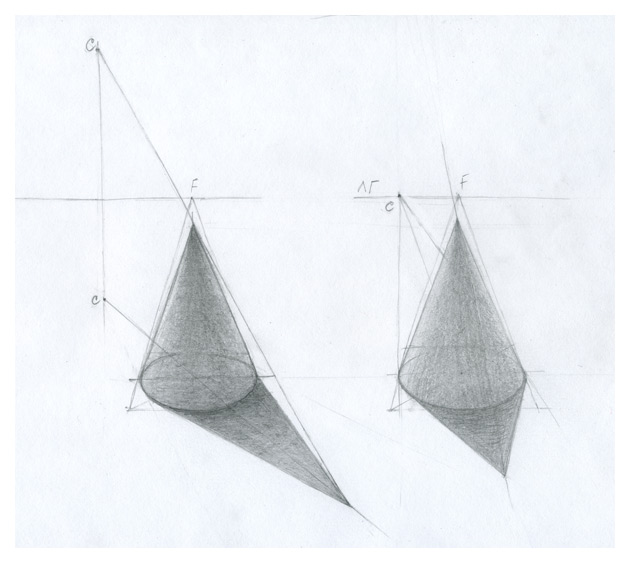Способ обратных лучей • Построим тень от наклонного ребра АВ на вертикальной
плоскости (подступенок) одной ступени.
• Проведем профильные проекции обратных лучей, затем
построим на фасаде тени 1 и 2 .
• Так как наклонное ребро АВ параллельно наклону лестничного
0
0
марша, проекции точек тени, аналогичные построенным, будут
60 располагаться на остальных ступенях на вертикальных прямых.

61. Способ обратных лучей

• Тени на ступенях лестницы
• Тенеобразующими ребрами боковой стенки являются
вертикальное, наклонное и горизонтальное ребра.
• Построим тень от наклонного ребра на вертикальной плоскости
(подступенок) одной ступени.
• Проведем профильные проекции обратных лучей, затем
61
построим на фасаде тени 12т и 22т.

62. Способ вспомогательных плоскостей уровня

62

63. Способ лучевых сечений

А
Р
Ат
а
63
Для построения падающей
тени от точки на плоскость
или поверхность следует
через точку провести
световой луч и построить
точку пересечения его с
плоскостью или
поверхностью.
Так как световой луч является
прямой линией, то
построение тени точки
сводится к построению
точки пересечения прямой
с плоскостью или
поверхностью

64. Способ лучевых сечений

64

65. Способ конусов и цилиндров

• Способ вспомогательных
касательных поверхностей
• Способ касательных (описанных или
65
вписанных) поверхностей конусов и
цилиндров применяется при
построении на фасаде контуров
собственных теней поверхностей
вращения без второй проекции.
Для построения точек,
принадлежащих контуру
собственной тени, используются
вспомогательные цилиндрические и
конические поверхности, тени
которых определяются просто.
Эти поверхности касаются заданной
поверхности вращения по
окружностям — параллелям.

66. Способ конусов и цилиндров

• Сначала применяют вспомогательные цилиндрические
поверхности, которые касаются поверхности вращения по
экватору или горловине, затем применяют касательные конусы,
соосные с данной поверхностью.
После этого определяют теневые образующие
вспомогательных поверхностей и отмечают точки их
соприкосновения с соответствующими параллелями данной
поверхности. Эти точки принадлежат контуру собственной тени
поверхности вращения. Полученные точки тени соединяют
плавной кривой.
При построении контура собственной тени прежде всего
необходимо построить характерные точки контура — точки
тени, лежащие на фронтальном и профильном очерках
поверхности (точки видимости), а также высшую и низшую
точки контура тени.
Первые две точки определяют с помощью касательных конусов
с углом наклона образующей 45°, а вторые две точки — с
66помощью конусов с углом наклона образующей 35 °

67. Построение собственной тени поверхности вращения

45о
350
35о
35о
45о
350
67
450
450

68. Построение собственной тени поверхности вращения

Применяя перечисленные выше
«стандартные» приемы построения теней
цилиндра и конусов, можно построить
необходимое число точек контура
собственной тени любой поверхности
вращения.
Рассмотрим пример построения контура
собственной тени выпуклой поверхности
вращения — о в о и д а.
Для построения точек тени на экваторе
поверхности опишем вокруг поверхности
соосный цилиндр и на окружности касания
определим общие точки тени 1′ и 2′.
Затем построим фронтальные проекции
вспомогательных касательных конусов с
углом наклона образующей 35°, проведя
касательные к очерку овоида до пересечения
с осью, а из этой точки — прямую под углом
45° к линии касания, получим высшую точку 3′
(невидимую) и низшую 4′.
68

69. Построение собственной тени поверхности вращения

• Конусы с углом наклона образующей
69
450 дадут на очерке поверхности
точки 5′ и 7′ и точки, совпадающие с
проекцией оси, 6′ (невидимая) и 8‘.
Если восьми точек окажется
недостаточно, проводят
дополнительную параллель
поверхности и строят касательный
конус произвольного вида (точки 9 и
10). Через полученные точки проводят
плавную кривую, в точках 5′ и 7′ она
должна коснуться очерка овоида.

70. Способ цилиндрических экранов

45о
35о
R1
R2
R3
R2
R3
70
R1

71. Задания для самопроверки Задачи

S2
45о
45о
S1
1. Построить тень вертикального круга
2. Построить тень горизонтального квадрата
3. Построить тень плоскости общего положения
71

72. Задания для самопроверки Задачи

S2
45о
45о
S1
1. Построить тень сферы
2. Построить тень параллелепипеда
3. Построить тень конуса
4. Построить тень пирамиды
72

Тени геометрических тел на ортогональных проекциях х х

Тени геометрических тел на ортогональных проекциях х х Разработала: Семенова Н. В.

Построение теней призм Собственная тень призмы х х Падающая тень призмы Падающая тень строится от неосвещенной части поверхности – собственной тени. Проекции световых лучей задают границы собственной тени, направление и ширину падающей тени. Световые лучи, направленные сверху вниз из наиболее значимых точек на фронтальной проекции, определяют длину падающей тени.

Построение теней призм Собственная тень призмы х х Падающая тень призмы Собственные и падающие тени призм представляют собой многоугольники. Падающая тень может преломляться и располагаться на двух плоскостях проекций.

Построение теней пирамиды Собственная тень пирамиды х Падающая тень пирамиды Собственная тень пирамиды

Построение теней пирамиды х х Падающая тень пирамиды

Построение теней конуса s’ s’ Собственная тень конуса S’т мн х Sт х Падающая тень конуса Собственная тень конуса При построении теней конуса вначале строится тень от вершины фигуры, затем определяются границы падающей и собственной тени.

Построение теней конуса о’ s ׳ Собственная тень конуса о’ х х Sт от от Падающая тень конуса

Построение теней цилиндра о’ 1′ 2′ 3’Ξ 5′ 4′ 2‘т х 1‘т 3‘т 4‘т 5‘т от х 1 Падающая тень невысокого цилиндра, расположенного на значительном расстоянии от фронтальной плоскости проекций находится на горизонтальной плоскости проекций 2 3 4 5 Падающая тень цилиндра преломляется. Она находится на горизонтальной и фронтальной плоскостях проекций

Построение теней цилиндра 1′ 2′ 3’Ξ 5′ 4′ 2‘т 1‘т 3‘т 4‘т 5‘т х 1 2 3 4 5

Построение теней цилиндра Боковая неосвещенная часть поверхности — собственная тень х Изображение падающей тени горизонтального цилиндра начинается с построения теней от оснований фигуры. Падающая тень такого тела состоит из теней от двух оснований (окружностей) и тени от боковой неосвещенной поверхности цилиндра.

ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ

Математика ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ

просмотров — 199

Как уже говорилось выше, падающая тень от геометрического образа является тенью от линии, являющейся контуром его собственной тени. По этой причине в общем случае вначале определяется контур собственной тени геометрического образа, а затем контур падающей. Далее рассматривается построение теней от простейших геометрических тел: параллелœепипеда, цилиндра, конуса, шара (сферы).

Тень от параллелœепипеда.Контур собственной тени параллелœепипеда ограничен прямыми линиями и в связи с этим построение теней от него не нуждается в комментариях (рис.4.1, 4.2). Необходимо лишь отметить, что если грани его параллельны плоскостям проекций, то ширина тени составляет величину a+b, ᴛ.ᴇ. сумму длин сторон основания.

Тень от цилиндра.Контур собственной тени вертикального цилиндра образован полуокружностью верхнего основания, полуокружностью нижнего основания и двумя образующими, которых касаются световые лучи (рис.4.3). По этой причине для построения падающей тени крайне важно построить в общем случае тени от верхней и нижней окружностей и двух образующих. На рис.4.4, 4.5, 4.6 показано построение теней для различных положений цилиндра в пространстве, а также половины цилиндра, примыкающего к фронтальной плоскости.

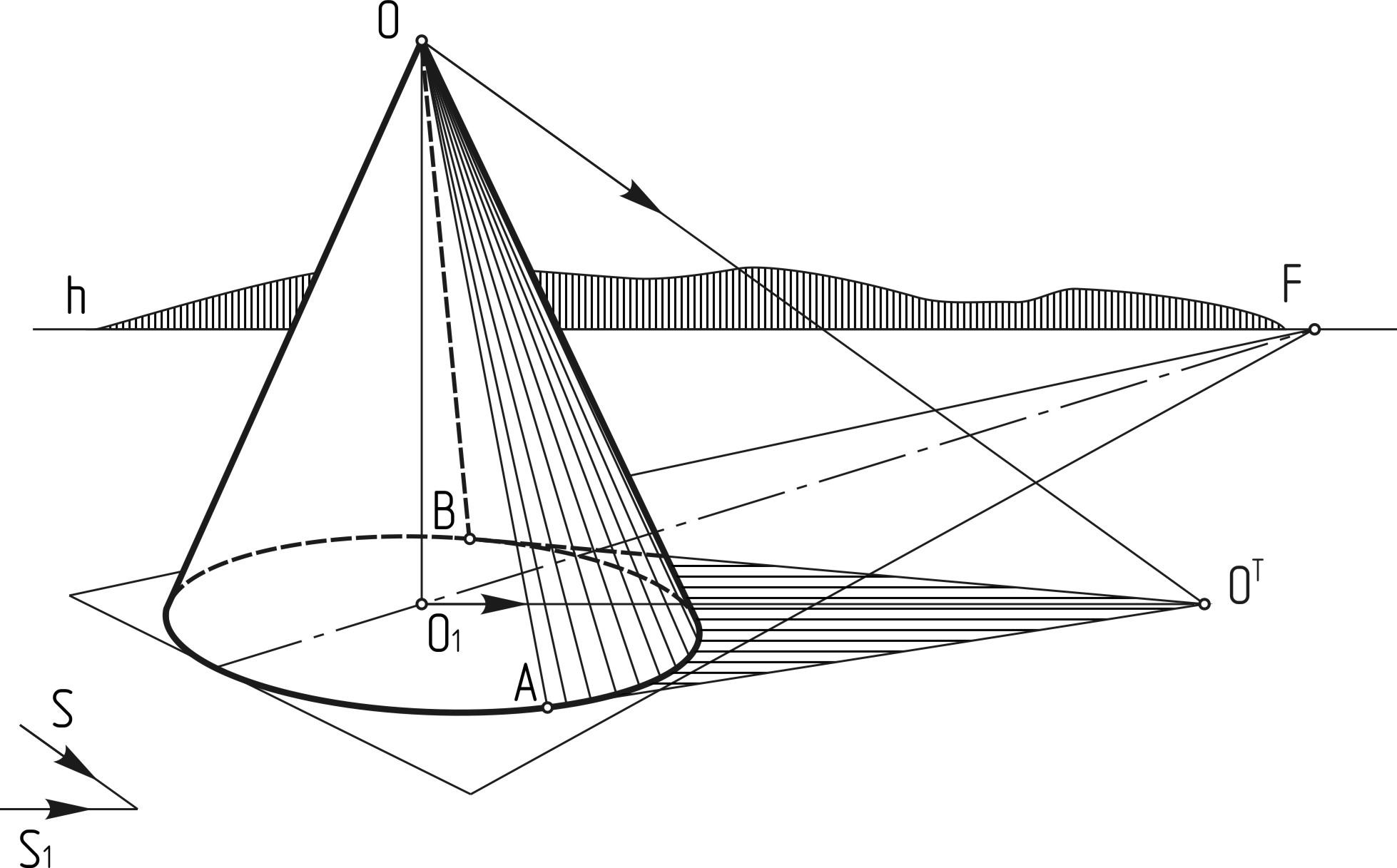
Тень от конуса.В отличие от других геометрических тел для конуса вначале строится падающая тень и лишь потом собственная. Для этого строится падающая тень от вершины конуса (рис.4.7). Из полученной точки S₁^т проводятся касательные прямые к основанию конуса. Контур, образованный этими касательными, и часть контура основания являются контуром падающей тени конуса. Образующие конуса, проведенные из точек касания, являются контуром собственной тени конуса. В случае если тень от вершины конуса падает на фронтальную плоскость, то строится, так называемая, фиктивная тень от вершины на горизонтальную плоскость, проводятся касательные к основанию конуса из этой точки, но только в пределах горизонтальной плоскости. Точки на линии пересечения плоскостей соединяются с истинной тенью от вершины (рис.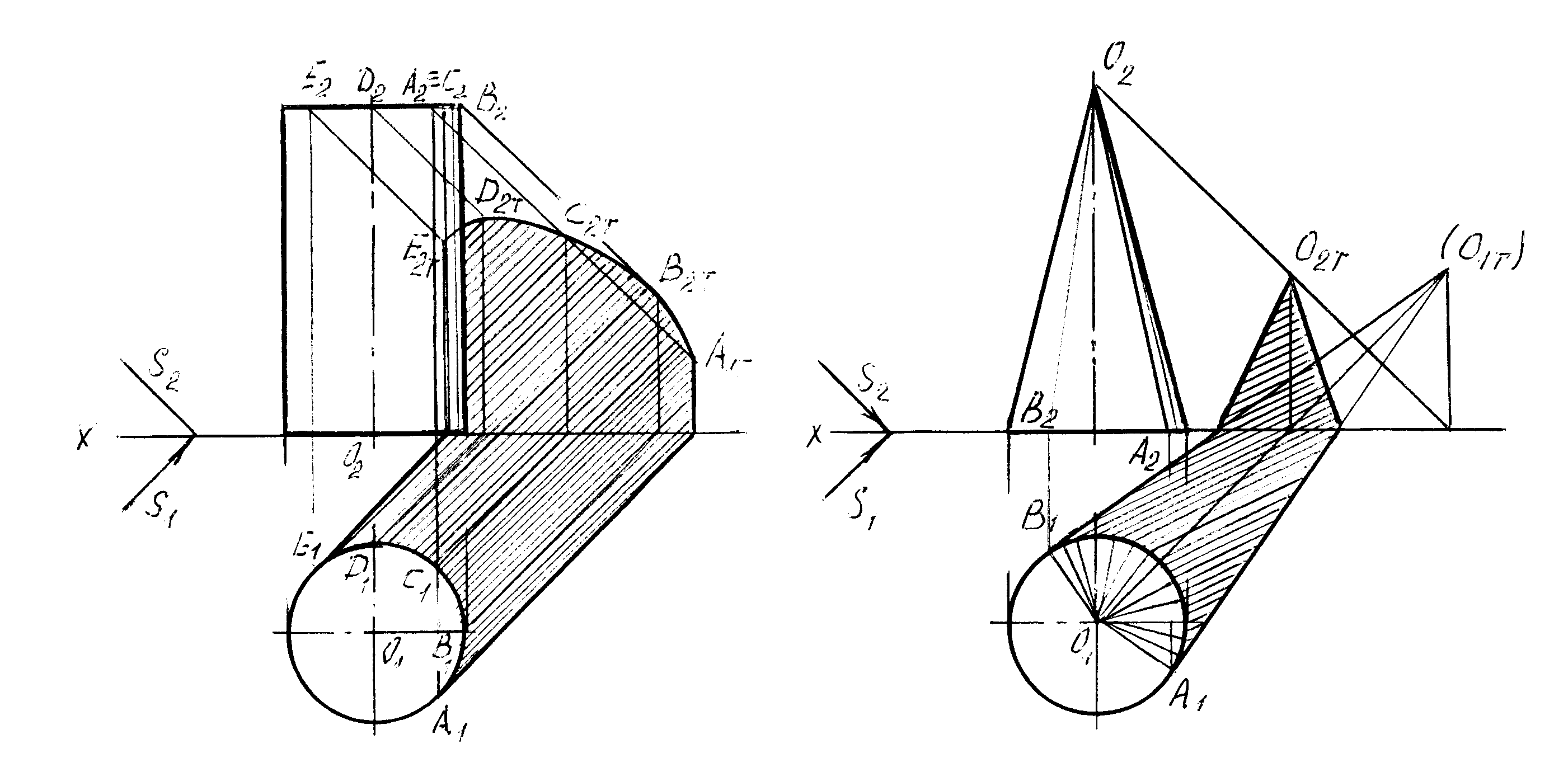 4.8).

В случае если конус обратный, для построения собственной тени строится фиктивная тень от вершины на плоскость, в которой находится основание конуса (рис.4.9) и из нее проводятся касательные к основанию конуса.

На рис.4.10 представлена половина конуса, примыкающего к фронтальной плоскости и отстоящего от горизонтальной плоскости. Контур падающей тени такого конуса образован контуром падающей тени окружности основания и прямой, исходящей из вершины, (т.к. вершина конуса лежит во фронтальной плоскости) и касательной к тени от окружности. В случае если из точки касания провести обратный луч до основания, то из полученной точки 1 можно провести образующую, являющуюся контуром собственной тени.

На рис.4.11 и 4.12 представлены два конуса, у которых углы при основании равны 45⁰ и 35⁰ соответственно. Контур собственной тени для конуса с углом 45⁰ при основанииобразуют профильная и контурная образующие. Контур собственной тени для конуса с углом 35⁰ при основании вырождается в прямую, являющуюся образующей, совпадающей со световым лучом. Конусы с углами, меньшими 35⁰, не имеют собственной тени. Боковая поверхность таких конусов полностью освещена и не дает падающей тени.

На рис.4.13 показано графическое построение угла 35⁰ .Для этого строится квадрат, размер диагонали 1 – 2 циркулем переносится на сторону квадрата͵ полученная точка 3 соединяется с точкой 4. Угол между отрезками 1 – 3 и 3 – 4 составляет 35⁰.

Конусы с углами при основании 45⁰ и 35⁰ в дальнейшем будут использоваться при построении теней более сложных форм, т.к. положение их собственных теней заведомо известно и легко строится.

Тень от сферы.Собственная тень сферы является эллипсом, большая ось которого равна диаметру сферы d, а малая ось приблизительно равна 0,6d (рис.4.14).

Дополнительные точки на контуре собственной тени можно построить проведением вертикальных и горизонтальных прямых из концов большой оси до пересечения с вертикальной и горизонтальной осями сферы. Смысл построений станет ясен при изучении способов построения теней. Падающая тень от сферы является эллипсом, для построения которого строится тень от центра сферы. Перпендикулярно направлению проекции светового луча расположена малая ось этого эллипса, равная по величинœе диаметру сферы. Величина большой оси определяется засечкой, равной диаметру сферы, из концов малой оси на направление большой и равна 1,7d. На рис.4.15 построена тень от полусферы на фронтальную плоскость проекций.

Читайте также

— ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ

Как уже говорилось выше, падающая тень от геометрического образа является тенью от линии, являющейся контуром его собственной тени. Поэтому в общем случае вначале определяется контур собственной тени геометрического образа, а затем контур падающей. Далее… [читать подробенее]

Рисование теней — Libtime

1. Главная
2. Рисование
3. Рисование теней

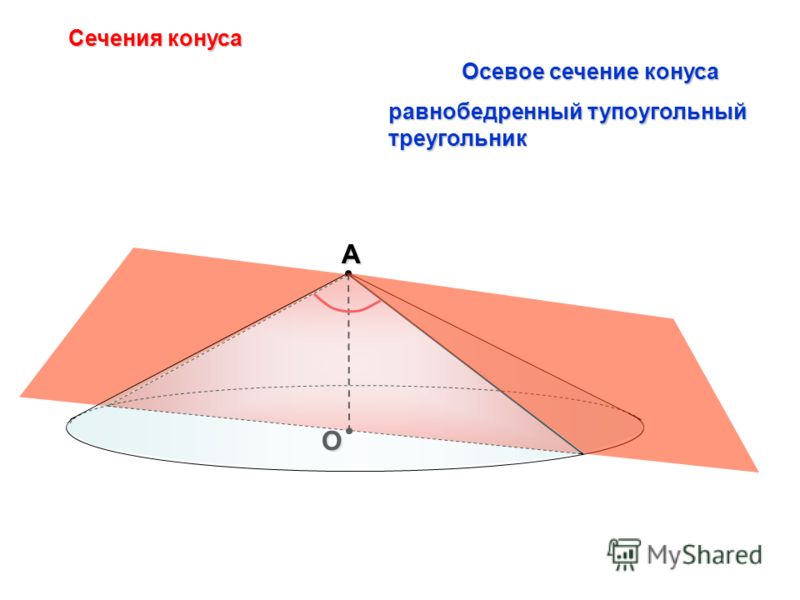libre14 Ноябрь 2012 13049 Обсуждение вопроса о рисовании теней выходит за рамки «проблемы изображения с натуры», но для полноты изложения сюда включены некоторые элементарные понятия об этом. Рисование теней грибов. Под интенсивностью тени мы подразумеваем степень затемненности предмета. Оттенки оказывают решающее влияние на развитие представления о пространственности тел. Различают тени собственные и падающие. Собственные тени мы наблюдаем на телах, под падающими подразумеваем тени, которые бросает источник света на места, куда лучи света вовсе не могут проникнуть или проникают лишь частично, так как им мешает тело. Иногда тень падает на край тела. Иногда части тела могут бросать тени на само тело. Тени различной степени затемненности нужно внимательно наблюдать и сравнивать, избрав одну площадь тела основной и сравнивая с ней степень затемненности крайних площадей. Тень мы наблюдаем, сильно прищурившись. Чем сильнее мы прищуримся, тем выразительнее выступят оттенки и пространственность тел. Рисунок 1 — Рисование тени карандашом. Недостатком школьных рисунков обычно бывает то, что они неточно отражают интенсивность затемненности падающих теней. На определении интенсивности теней можно упражнять изобразительное чувство учеников.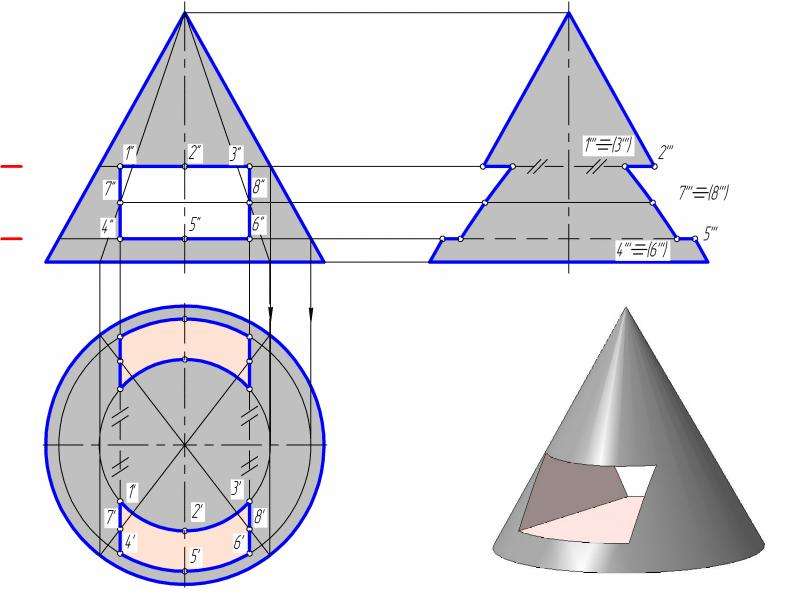 Давайте проведем небольшой урок рисования тени.

Рисование теней простым карандашом

На рис. 1А изображен античный дорический столб из белого мрамора, освещенный с левой стороны. Фоном его будет частично светлое небо, частично темная поверхность. Собственная тень будет на правой стороне столба. Самая темная тень окажется на краю, если фоном будет светлая площадь неба. Если за столбом находятся более темные поверхности, то на краю его появится отраженный свет, или световые рефлексы. Самая темная собственная тень в этом случае окажется левее от рефлексов, в интенсивность которых она будет постепенно переходить. Подобное явление наблюдается, как видно на рис. 1В, на круглых естественных предметах. Падающую тень круглого тела мы будем видеть эллипсовидной (рис. 3В). В связи с тем, что в классах больше окон, через которые проникает свет, за телом появляется больше эллипсовидных теней. Когда их прикрывают, возникает более темная теневая площадь. Наиболее темной падающая тень будет там, где прикрыты все эллипсы. Менее интенсивной будет тень там, где прикрывают тени двух эллипсов. Неприкрытые тени при освещении постоянной интенсивности будут наименее темными. Падающая тень дает на краю круглого стола отраженный свет, или рефлекс. На примере ребристых тел, пользуясь искусственным светом, преподаватель объясняет ученикам принцип построения падающих теней. Рисунок 2 — Принцип построения падающих теней. Рисунки следует выполнять теоретически. На рис. 2А освещен боковой стержень, падающую тень от которого мы должны наблюдать и изобразить. Падающая тень отходит от самой низкой точки стержня, и, так как осветительный прибор помещен на плоскости фасадной прямой, проходящей через самую нижнюю точку стержня, направление падающей тени на горизонтальной поверхности будет изображено горизонтально. Если бы осветительный прибор находился ближе к нам, направление падающей тени на рисунке отклонялось бы немного вверх. Если бы осветительный прибор был отодвинут несколько за фасадную плоскость (рис. 4А), тень отклонилась бы несколько вниз. Длина тени зависит от высоты осветительного прибора: если мы ведем касательную осветительным прибором к самой высшей точке стержня, световой луч в воздухе определяет длину падающей тени на поверхности. Падающая тень вершины В будет в конечной точке падающей тени стержня, в В’. Падающая тень точки А, точка А’, будет идентична с точкой А. В связи с тем, что при рисовании падающей тени с натуры мы предполагаем естественный осветительный прибор – солнце, от которого лучи расходятся центрально, во все стороны, мы должны были бы изображать тени по принципам центрального освещения. Но солнечные лучи излучаются на таком расстоянии, что в пучке они почти параллельны. Поэтому для упрощения при конструированных падающих тенях мы принимаем во внимание направление параллельных лучей. Для изображения направления падающих теней необходимы два элемента: направление падающей тени (на поверхность) и направление светового луча (в воздухе). Слова «в воздухе» и «на поверхность» мы применяем в школьном обучении для более наглядного объяснения понятий. Падающая тень стены (рис. 3А). Речь идет о падающих тенях двух стержней, вершины которых соединяем. Будет ли стена освещена или будет она в тени, определяем ее форму по направлению падающих теней. Сторона поверхности, на которую падает это направление, будет освещена, обратная – затемнена. Рисунок 3 — Рисование тени стены.

Рисование падающей тени ребристого тела

Строим падающие тени трех вертикальных ребер (рис. 3В). Подвинув направление падающей тени по поверхности к основанию тела, увидим, какие ребра образуют предел собственной тени. Прежде всего направление падающей тени натолкнется на точку А основания, затем на С, а потом на Е. Ребро в точке А будет передним пределом, ребро в точке Е – задним пределом собственной тени. Увидев, благодаря перемещению направления падающей тени на поверхности, что ребра АG к GЕ освещены, мы ставим перед собой задачу изображения падающих теней ребер АВ, СD и ЕF.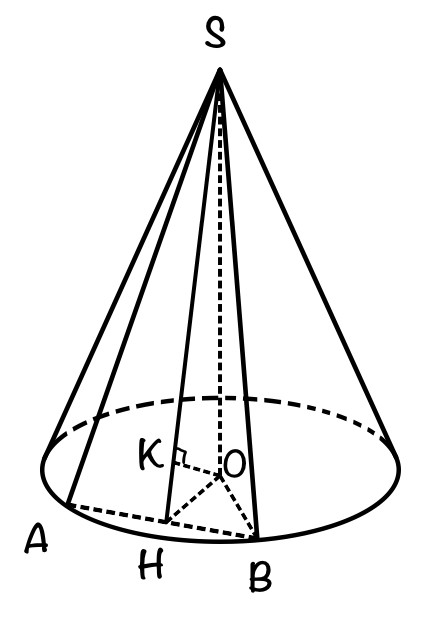 Падающие тени их вершин мы соединим и ограничим предел падающей тени.

Рисование падающей тени цилиндра

Для того чтобы установить поверхностные прямые, обозначающие предел собственной тени, мы снова подвинем направление падающей тени на поверхности к основанию цилиндра. Из первой точки соприкосновения A и из последней точки Z будут выходить пределы теней – собственной и падающей. Дуга падающей тени будет исходить из падающей тени вершины В и Y. Если бы восстановить поверхностные вертикальные абсциссы на дуге эллипса между точками А и Z и построить их падающие тени (падающие тени их вершин между В и Y), то они ограничили бы кривую часть эллипса на поверхности. Падающая тень вершины В будет в В’, точки Y – в Y’. Рисунок 4 — Рисуем падающую тень цилиндра и круглого тела. Куда падает падающая тень цилиндра, установим с помощью касательной, построенной к верхнему основанию, к верхнему эллипсу. Она будет параллельна направлению светового луча в воздухе.

Рисование падающей тени шара

К шару проводим касательные, параллельные направлению светового луча в воздухе. Соединение касательных является большой осью эллипса собственной тени. Продолженное направление касательных ограничит длину эллипса на поверхности. Падающая тень конуса. Строим падающую тень высоты конуса. Можете ознакомится с тем, как рисовать конус в статье 7 способов перспективного рисования. От точки А ведем линию, параллельную направлению падающей тени на поверхности, из вершины V – прямую линию, параллельную направлению светового луча. От падающей тени вершины, из V’, проводим касательные к основанию. Из точек соприкосновения строим поверхностные прямые к вершине V, образующие предел собственной тени на конусе.

Рисуем тень от конуса и пирамиды

Нужно обратить внимание учеников на то, что у тел формы конуса и пирамиды падающие тени ни в коем случае не бывают на поверхности прямыми. Рисунок 5 — Рисование падающей тени конуса и пирамиды. Падающая тень пирамиды строится подобным же образом. Прежде всего, строим падающую тень высоты пирамиды. От падающей тени вершины рисуем касательные к основанию. Они образуют предел падающей тени на горизонтальной площади. Ребра тела, выходящие из точек соприкосновения основания, образуют предел собственной тени пирамиды. Усеченная пирамида и конус. Прежде всего, строим падающую тень целого конуса и пирамиды без усечения, потом собственную и падающую тень внутреннего цилиндра или призмы. Последовательность работы описана выше. Ломаные тени. Ломаные тени, попадающие на вертикальную наклонную и цилиндрическую поверхность, изображены на рис. 6А, В, С. Рисунок 6 — Рисуем ломанные тени конуса и усеченного конуса Падающие тени, наблюдаемые на телах. На телах, которые изображаем с натуры, мы не конструируем ни падающих, ни собственных теней. Мы изображаем оттенки теней и рефлексов такими, какими они нам кажутся, когда мы опять прищуриваем глаза. Мы тщательно определяем оттенки краев соседних тел, сравниваем, где тень темнее, где она наиболее темная. Степень затемненности тени сравниваем с одной основной поверхностью.

Рейтинг: 5/5 — 2 голосов

«Построение границ света и тени. Конус»

Дата:

Класс: 1 «г»

Предмет: рисунок

Тема урока: «Построение границ света и тени. Конус» 3часа

Цель:

Задачи:

Тип занятия:

Материалы и оборудование:

Структура урока:

1 урок

Орг. момент

Актуализация

Объяснение нового материала

2 -3 урок

Практическая часть

Анализ работ:

Выполнить построение конуса в вертикальном положении

обучающая:научить строить конусный предмет, расширить представление о линейном рисунке;

развивающая: развить умение анализировать форму предмета, умение, наблюдательность и усидчивость, развить глазомер;

воспитывающая: воспитать любовь к изобразительному искусству, к предметам окружающего мира, культуру работы с графическим материалом;

комбинированный (рисунок с натуры)

для учителя: наглядные пособия- поэтапность построения конуса; работы учащихся ДХШ.

для учащихся: бумага, карандаш, ластик;

1. Орг.момент (1-2 мин)

2. Актуализация (10 мин)

3. Объяснение нового материала (35 мин)

4. Практическая работа (90 мин)

5. Анализ работ (3 мин)

Ход урока

Здравствуйте, ребята! (Проверяю готовность к уроку). Сегодня мы будем учиться выполнять построение конуса в вертикальном положении.

— Ребята, а какие геометрические тела вы знаете?

Ответы учащихся.

— Это ребята, цилиндр, конус, призма, шар, круг.

-Ребята, а что такое конус?

Конус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. В нашем случае конус прямой, его ось перпендикулярна основанию.

Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.

Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания.

Следующий этап — построение эллипса. При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина.

Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее.

Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму.

Композиционное размещение предмета на формате.

Снизу оставляем больше места. Предмет размещаем в середине листа, потому как он один. Предмет не должен быть слишком большим и слишком мелким. Также не забываем о падающей тени.

При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа.

Линии конструкции.

Определив высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса.

Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.

Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми.

Чтобы передать объём в линии, ближнюю часть овала сделаем темнее.

После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба.

Выполнение в тоне.

Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.

Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали. Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму. Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы

.

В процессе работы учеников, провожу индивидуальную работу. Анализирую характерные особенности.

Вывешиваем работы на доску. Задаю вопросы:

-Ребята, посмотрите на работы…

— Видите ли вы ошибки в работах? Какие?

— Чью работу можете назвать аккуратной?

-Как вы думаете, какая работа получилась правильно?

Ответы учащихся.

-А какие ошибки вы видите в работах?

Ответы учащихся.

— Почему так получилось?

Ответы учащихся.

— Как вы думаете, кому удалось передать светотеневые отношения в конусе?

Ответы учащихся.

Тень собственная — Энциклопедия по машиностроению XXL

В общем случае такая графическая модель содержит три различных тона свет, тень собственную и тень падающую. В частных случаях возможны объединения тонов любых двух областей. Для построения падающих теней требуется использование аппарата параллельного проецирования. Наглядность получаемого изображения зависит от характера пространственной сцены и от выбора направления проецирования (светового луча). В некоторых случаях конфигурация падающей тени привносит дополнительную геометрическую характеристику формы, ее пространственного расположения, тем самым в значительной мере повышая выразительность изображения. Но, с другой стороны, в световую зону и в зону собственной тени попадают грани, различным образом ориентированные в пространстве. Тональное же их решение в этой графической модели одинаково.  [c.55]
Можно отметить следующие элементы светотени (рис. 12.29) свет, полутень и тень (собственную и падающую). На затененной части имеется рефлекс, а на освещенной — блик.  [c.171]

Тень собственная — часть поверхности предмета, которую не достигают лучи света.  [c.172]

Различают собственные и падающие тени. Собственной тенью называется тень, получающаяся на неосвещенной части поверхности некоторого объекта при освещении его какими-либо источниками света тень же, отбрасываемая этим объектом на какую-либо другую поверхность, называется падающей. При этом, если световые лучи, освещающие объект, исходят из одной (собственной) точки А, то тень называется факельной-, если же световые лучи параллельны между собой (иначе исходят из бесконечно удаленной точки А ), то тень называется солнечной. Мы ограничимся построением лишь солнечных теней, которые имеют большее практическое значение.  [c.395]

Что такое тень падающая, тень собственная, блик  [c.41]

Сумма их служит для вычис.тения собственной частоты вертикальных колебаний рамы  [c.499]

Изображенная на рисунке освещенная часть поверхности предметов называется светом (рис. 257), а неосвещенная— тенью. Различают тени собственные — на поверхности предмета, куда не достигают лучи, идущие от источника света, и падающие, которые получаются на освещенной части поверхности из-за того, что на пути лучей света расположены другие предметы.  [c.208]

Тени однополостного гиперболоида вращения (рис. 229). Собственная тень поверхности построена способом касательных поверхностей. К четырем параллелям поверхности проведены касательные поверхности — цилиндр III), два прямых конуса I и II) и один конус, обращенный вершиной вниз IV), с помощью которых построены восемь точек контура тени. Г оризонтальная проекция собственной тени построена с помощью линий связи. Падающая тень от поверхности на плоскости Я построена с помощью теней трех параллелей. Плавные кривые, огибающие тени параллелей и основание поверхности, представляют собой контур падающей тени. Собственная тень поверхности могла быть также построена способом обратных лучей. Из точек касания контура падающей тени к теням параллелей, например из точек IVh V, проводят обратные лучи до пересечения с соответствующими проекциями параллелей (штриховые линии).  [c.172]

Светотень состоит из собственной тени, падающей тени, рефлекса, полутона и блика (рис. 192).  [c.104]

На рис. 1.5.1 представлен пример, требующий для светотеневой характеристики пространственной сцены построения трех областей области, непосредственно освещенной источником света, области отброшенной тени и области собственной тени (обращенной в сторону источника света).  [c.55]

К построению плоскости, параллельной данной прямой (световому лучу) и касательной к конусу или цилиндру, приходится прибегать при определении контуров собственной и падающей тени. Если эти тела стоят на горизонтальной плоскости (земле), удобно пользоваться горизонтальными следами плоскостей (см. черт. 291).  [c.132]

Исследуя взаимное расположение световых лучей относительно плоскости данной фигуры, определяют освещенность проекций этой фигуры. Пример определения собственной тени треугольника AB приведен на черт. 447. Прежде всего через точку D, лежащую внутри контура треугольника, проводят световой луч DK. Далее устанавливают относительное располо-  [c.202]

ABS, которая окажется освещенной, так как она обращена к источнику света. Остальные грани тетраэдра находятся в собственной тени. Эпюрное решение данной задачи представлено на черт. 453,, где сначала построена тень тетра-адра на П,, а затем с помощью реальной тени Хп2 найден контур падающей тени на П .  [c.207]

На черт. Л11-—А19 построены собственные и падающие тени прямоугольного параллелепипеда при трех различных положениях источник света.  [c.219]

На черт. 480 и 481 дано построение тени пирамиды и конуса. В обоих случаях прежде всего найдены тени вершин (точки Ц, ), из которых затем проведены прямые L A и Ln, D. На черт. 480 это будут тени тех ребер, а на следующем — тени тех образующих, которы.ми определяются контуры собственных теней рассматриваемых геометрических тел.  [c.219]

Описанный путь построения контура собственной тени дает более точный результат, чем тот, когда применяют обратные лучи.  [c.226]

I раней в собственной тени оказались правые.  [c.226]

При заданном направлении светового луча из видимых в собственной тени оказались правые грани. Построение падающих теней не вызывает затруднений.  [c.226]

Опреде.тение напряженного состояния в конструкции, т. е. определение величины и вида напряжений в элементах конструкций. Эти напряжения состоят из рабочих напряжений, возникающих от внешнего нагружения (вес груза, давление и др.) или связанных с условиями эксплуатации (например, температурные напряжения) собственных напряжений, возникающих при сборке, сварке и т. д.  [c.37]

Контур собственной тени  [c.171]

Иногда технический рисунок выполняют с еще большим упрощением показывают только собственную тень, а падающую нигде не показывают. Такое упрощение сильно облегчает построение, но при этом теряется выразительность изображения.  [c.172]

При построении падающей тени от параллелепипеда (рис. 423) сначала определяют падающие тени от его вертикальных ребер. Полученные на предметной плоскости точки Л , Е , 5 соединяют прямыми, которые определяют падающую тень от параллелепипеда. Ребра Л — 1 и Е — 3 являются границей собственной тени. Собственная тень наиболее темная на границе светораздела, т. е. возле ребра А — 1. Падающая тень должна быть темнее собственной. Наиболее темное место у падающей тени расположится возле ребра I—4. Далее тень несколько ослабевает, т. е. становится светлее.  [c.277]

Собственная тень — теиь, находящаяся в неосвещенной части предмета.  [c.104]

Рефлекс — высветление собственной тени благодаря отраженным лучам света.  [c.104]

Основная задача теории теней заключаегся в определении контуров собственной и падающей теней данного тела.  [c.199]

Условимся собственными нашвать тени, которые получаются на неосвещенной поверхности самого тела тени, отбрасываемые нреО-метом на плоскости проекций, а также на Ору-, ме поверхности, будем именовать падающи и.  [c.199]

Пример 2. no rpoHi b собственные и падающие тенн конусов и цилиндров, различно расположенных в пространстве.  [c.211]

Построение собственной и падающей юней цилиндра (черт, 463) отличается от пpг l..j i. ie-го только тем, что вместо тени верпшнь чри-пиюсь определить падающую тень вюр> 0 (верхнего) основания.  [c.211]

Пример 3. Построить собственную и падающую тени нелинейчаюй поверхности вращения общего вида (черт. 468).  [c.213]

Дополнительные построения, которые приходится выполнять, если световые лучи не параллельны плоскостям проекций, показаны на черт. 469. Здесь прежде всего построены новые проекции (s и. Vj) светового луча, поверну гого на угол Ф до положения, параллельною Hj. Затем, согласно изложенной выше методике, найдена проекция точки A , принадлежащей контуру собственной тени. Остается проделать обратное преобразование эпюра, )aкJlючaю-1цееся в повороте найде1шых точек вокру оси поверхности вращения на угол Ф против дни-жения часовой стрелки.  [c.215]

Менее удачным следует признать то положение точки. S , гфи котором вертикальные плоскости видимых граней параллелепипеда оказались в собственной тени, а падающая гень наплывом идет к зрителю (черт. 478). Очевидные удобства построения присущи случаю, когда световые лучи параллельны плоскости картины (черт. 479). Следует иметь в виду, что при этом параллельны между собой не только вторичные проекции, 1ю и сами световые. 1учи.  [c.219]

На черт. 482 представлен пример посл роения собственных и падающих теней прямого цилиндра, основание которого находится на плоскости П,.  [c.219]

Тс)чки касания /), и й, определяют те образующие АА, и 5iSi, которые принадлежат контуру собственной тени. Этот контур замыкается дугой ADB верхнего основания. Найдя тени точек указанной дуги на предметной плоскосги, заканчиваем поаросиис падающей i iin.  [c.219]

Рефлекс — высветление собственной тени за счет освещения теневой стороны предмета отраженными лучами от окружающих освещенных предметов или поверхностей данного предмета.  [c.172]

---

Как сделать тень в форме конуса?

К сожалению, я не думаю, что это возможно с любым из типов света по умолчанию в Unity. Направленный свет предназначен для локальных сцен на уровне земли, где солнце находится так далеко, что имеет смысл смоделировать его расстояние как бесконечное, то есть настолько далеко, что его лучи примерно параллельны. Очевидно, что это не сработает, если ваш прицел — это вся солнечная система.

Тени, которые вы описываете, требуют, чтобы вы смоделировали источник света, который, как вы правильно догадались, имеет ненулевую область .Точечные источники света — это именно то, что вам нужно — одна точка. Из любой другой заданной точки в вашей сцене существует либо полностью беспрепятственных линий от точки до источника света, либо объект таким образом, что полностью перекрывает источник света. Ничего среднего — источник света никогда не виден частично. По этой причине тени также не имеют автоматически физически правильной полутени. Без попытки подделать тень меняется от полной темноты («тени») до полностью освещенной области.

Ни один из источников света в Unity не использует сферическую область, как солнце. Единственная область Area Light Source Unity — это прямоугольная плоскость (например, поверхность люминесцентной потолочной лампы), которая работает не в реальном времени, а только при запекании карты освещения.

Итак, в заключение: вам не повезло — он не поддерживается из коробки в Unity. Если вы этого хотите, вам придется сделать это самостоятельно с нуля, что будет сложно и, несомненно, очень познавательно.Но с другой стороны, это звучит настолько полезным, что, если вы все-таки реализуете его, вы, вероятно, сможете упаковать и продать его в магазине активов. 😉

Изменить:

В качестве приближения, которое вы можете попробовать, которое не потребует от вас разработки локальных источников света с нуля, вы можете попытаться имитировать его, сделав свое солнце кластером точечных источников света вместо одиночного точечного света посередине. Поместите группу индивидуально более слабых точечных источников света на равномерно распределенных позициях на поверхности сферы, которую вы используете для солнца.Это может приблизить вас к желаемому результату без какого-либо программирования.

Если вы выберете это приближение, то помните, что шейдеры подчиняются верхнему пределу для пиксельного освещения, который установлен в настройках качества в меню Правка-> Настройки проекта-> Качество. По умолчанию — 4. Сбалансируйте это число с количеством источников света, которое вам нужно, чтобы повлиять на каждую планету, по сравнению с падением производительности.

теневой конус в предложении

SentencesMobile

• Ось теневого конуса едва проходит мимо юга Земли.
• Расчеты Паскуале Трикарико с использованием теневого конуса примерно за 40 минут до входа в атмосферу.
• Красный: определение формы теневого конуса; Зеленый: определение расстояния и направления поверхность-подповерхность с известной формой теневого конуса.
• Красный: определение формы теневого конуса; Зеленый: определение расстояния и направления поверхность-подповерхность с известной формой теневого конуса.
• Гиппарх наблюдал (во время лунных затмений), что на среднем расстоянии Луны диаметр теневого конуса равен 2+ лунным диаметрам.
• Также весьма вероятны события многократного рассеяния, что усложняет анализ. «Важно», что из-за используемых ионов с более низкой энергией LEIS обычно характеризуется «большими поперечными сечениями взаимодействия» и радиусами теневого конуса.
• В таблице указаны дата и время наибольшего затмения (в динамическом времени, которое в данном случае является временем, когда ось конуса тени Луны проходит ближе всего к центру Земли).
• Максимальное кольцевое пространство всегда будет превышать максимальное общее, потому что теневой конус в первом случае длиннее (поскольку Луна находится дальше от Земли) и расходится: таким образом, ширина тени намного больше.
• Список содержит дату и время наибольшего затмения (в динамическом времени, которое в данном случае является временем, когда ось конуса тени Луны проходит ближе всего к центру Земли; это во всемирном времени).
• «С научной точки зрения, красные лучи солнечного света изгибаются атмосферой Земли в теневой конус Земли» и все еще отражаются от затменной Луны, — сказал Джек Хоркхаймер, ведущий «Звездного наблюдателя» на PBS и директор космического транзитного планетария Майами. .«На самом деле мы видим все восходы и закаты вокруг Земли, одновременно отраженные от Луны.
• Трудно увидеть конус тени в предложении.

Что такое тень Земли и когда ее можно увидеть? | Земля

Посмотреть на фотографиях сообщества EarthSky.| Стефани Лонго сделала этот снимок утром 2 февраля 2020 года в государственном парке Элевен-Майл-Каньон в Колорадо. Она сказала: «Меня угостили демонстрацией тени Земли и пояса Венеры над континентальным водоразделом. Горы Разрыва были слишком далеко для быстрого выстрела, и мои пальцы онемели до боли, поэтому я решил снимать этот большой холм под названием Спинни-Маунтин ».

Как и все миры, вращающиеся вокруг Солнца, Земля отбрасывает тень. Тень Земли простирается примерно на 870 000 миль (1.4 млн км) в космос. Вы можете этого не осознавать, но с поверхности Земли вы можете видеть тень. На самом деле, это легко увидеть, и вы, вероятно, уже видели это много раз, когда день сменяется ночью.

Это потому, что сама ночь — это тень. Когда наступает ночь, вы стоите в тени Земли.

Лучшее время для наблюдения за земной тенью — это когда она подкрадывается к вашей части Земли … Как и все тени, тень Земли всегда находится напротив Солнца.Итак, вам нужно смотреть на восток после захода солнца в поисках тени (или на запад перед восходом солнца).

Тень Земли — это темно-синяя линия над горизонтом на фотографии Йоргена Андерссона из Швеции. Увеличить. | Ночь наступает, когда часть Земли, на которой вы стоите, входит в тень Земли. Изображение предоставлено НАСА.

Тень темно-сине-серая, она темнее синевы сумеречного неба. Розовая полоса над тенью называется поясом Венеры.

Тень Земли большая. Возможно, вам придется повернуть голову туда-сюда — вдоль дуги горизонта напротив солнца — чтобы увидеть все целиком.И, чтобы вам было легче распознать это, помните, что тень изогнута точно так же, как изогнута вся Земля.

И, как только вы его заметите, не возвращайтесь внутрь. Подождите немного и наблюдайте, как тень Земли поднимается на востоке с той же скоростью, что и солнце садится за ваш западный горизонт.

Тень Земли — это синяя линия у горизонта за голыми деревьями на этой фотографии Элис МакКлюр, сделанной в ноябре 2017 года. Розовая полоса над тенью — Пояс Венеры.Чтобы увидеть тень Земли, необязательно находиться в сельской местности. Сучета Випат поймала тень Земли и пояс Венеры облачным августовским вечером в Лондоне.

Тень Земли простирается так далеко в космос, что может касаться Луны. Вот что такое лунное затмение. Это луна в тени Земли.

Когда Солнце, Земля и Луна выровнены в пространстве (почти или идеально), а Земля между Солнцем и Луной, тогда тень Земли падает на лицо Луны. Именно тогда люди на Земле видят, что тень постепенно превращается в яркую полную луну в темную во время лунного затмения.

Если смотреть с поверхности Земли, обычно бывает два или более лунных затмения каждый год. Некоторые из них являются полными, некоторые частичными, некоторые представляют собой неуловимые затмения, известные как полутеневые.

Во время лунного затмения очень небольшое количество солнечного света просачивается через атмосферу Земли на тень Земли на Луне. Вот почему — в средней части полного лунного затмения — тень на Луне выглядит красноватой.

Гуру по затмениям Фред Эспенак из Аризоны, чьи расчеты затмений были основой наблюдений за затмениями на протяжении десятилетий, написал о полном лунном затмении 31 января 2018 года: «Какое чудесное полное лунное затмение! Это был мой 30-й и первый раз, когда я видел, где заходит луна во время полноты.Майк О’Нил представил этот великолепный снимок лунного затмения 31 января 2018 года. Он писал: «Не мог полностью добраться до полной, пока облака не накатились над северо-восточной Оклахомой».

Еще один способ узнать о тени Земли — просто подумать о ней так, как она видна из космоса.

На изображении ниже представлен прекрасный глобальный вид на Землю в ночное время. Это составное изображение, составленное из данных, полученных спутником Suomi National Polar-orbiting Partnership (Suomi NPP) за девять дней в апреле 2012 года и 13 дней в октябре 2012 года.

Темная часть, конечно же, тень Земли.

Изображение предоставлено НАСА.

Итог: ищите тень Земли как на вечернем, так и на утреннем небе. Это сине-серая тьма в направлении, противоположном солнцу, темнее сумеречного неба. Розовая полоса над тенью — на востоке после захода солнца или на западе перед рассветом — называется поясом Венеры.

Дебора Берд

Просмотр статей

Об авторе:

Дебора Берд создала серию радиостанций EarthSky в 1991 году и основала EarthSky.org в 1994 году. Сегодня она является главным редактором этого сайта. Она выиграла целую плеяду наград от радиовещательного и научного сообществ, в том числе за создание астероида 3505 Берд в ее честь. Бэрд, научный коммуникатор и педагог с 1976 года, верит в науку как в силу добра в мире и жизненно важный инструмент в 21 веке. «Работать редактором EarthSky — все равно что устраивать большую глобальную вечеринку для крутых любителей природы», — говорит она.

.