Тетраэдр как рисовать – Как построить тетраэдр 🚩 как собрать октаэдр 🚩 Математика

Как построить тетраэдр 🚩 как собрать октаэдр 🚩 Математика

25 мая 2011

Автор КакПросто!

Тетраэдр – это одна разновидностей многогранника, он состоит из четырёх граней, являющихся треугольниками, в каждой вершине тетраэдра сходятся по три грани. Тетраэдр называется правильным, если все его грани являются правильными треугольниками, все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.

Статьи по теме:

Инструкция

Для получения правильного тетраэдра необходимо построить куб – правильный многогранник, каждая грань которого является квадратом.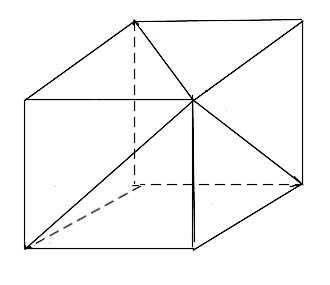 В построенном квадрате необходимо взять одну из его вершин, например, вершину A. К этой вершине сходятся три квадратные грани равны между собой как диагонали граней куба, поэтому фигура ABCD является правильным тетраэдром.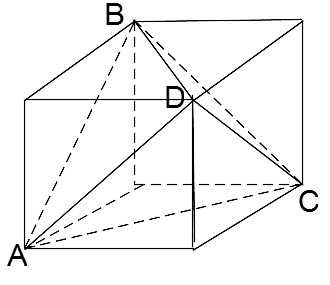

Обратите внимание

Тетраэдр является одним из пяти возможных правильных многогранников. К правильным многогранникам относятся так же: октаэдр, додекаэдр, икосаэдр и гексаэдр или куб. Куб – простейший для построения многогранник, все остальные могут быть построены с его помощью.

www.kakprosto.ru

Как нарисовать тетраэдр карандашом поэтапно. Пирамида

Одно из величайших чудес мира — пирамиды Египта, сохранились до наших дней. Более того, каждый год множество туристов отправляются в Гизу лишь для того, чтобы увидеть пирамиды и Сфинкса, который как будто охраняет сооружения, неподвижно застыв среди руин древнего храма.

Чтобы заинтересовать ребенка, можно рассказать ему следующее:

• До сих пор никто не знает, каким образом и для чего были построены пирамиды. Ученые выяснили, что это чудо света было построено намного раньше, чем появилось Египетское царство.
• Несмотря на то, что в древние времена не было современной техники, пирамиды построены с математической точностью.
• На протяжении трех тысяч лет пирамида фараона Хеопса была самым высоким сооружением в мире.

Нарисовать пирамиды очень просто. Следите за нашей инструкцией и у вас все получится. Вам понадобятся: лист бумаги; карандаш; ластик; линейка;
Шаг 1

Место для пирамид

Для начала рисуем прямоугольник, в котором будем размещать пирамиды. Чтобы облегчить процесс, можете воспользоваться линейкой.
Далее делим прямоугольник на три части. У вас должны получиться два прямоугольника слева и справа, а в центре квадрат, немного больше, чем прямоугольники.

Шаг 2

Первая пирамида

На этом этапе начинаем рисовать пирамиды. Для начала изображаем пирамиду в первом прямоугольнике. Ее еще называют пирамидой Хефрена. Она вторая по величине и находится перед остальными. Заметьте, что часть треугольника выходит за прямоугольник.

Шаг 3

Вторая пирамида

Пришла очередь Великой или пирамиды Хеопса. Она начинается в первом прямоугольнике и выходит за грани второго. Верх треугольника касается верхней стороны квадрата.

Шаг 4

Третья пирамида

Последняя пирамида фараона Микерина самая маленькая. Ее мы рисуем только в прямоугольнике, не выходя за грани. Часть этого сооружения спрятано за Великой пирамидой.

Шаг 5

Убираем лишние линии

Теперь нужно стереть все ненужные линии. Остаются лишь пирамиды. Полностью нарисована только первая, так как остальные спрятаны друг за другом.

Шаг 6

Рисуем кирпичи

От верхушек пирамид проводим прямые линии вниз, обозначая углы.
По всей первой пирамиде проводим горизонтальные линии.
Эти линии через небольшие промежутки разделяем вертикальными линиями, обозначая кирпичи.
Рисуем горизонтальные линии на оставшихся пирамидах.
Аналогично разделяем линии, чтобы получились кирпичи.

В древности люди были не особо дальновидными и оптимистическими, и вовсе считали, что люди от силы проживут до 2012 года, а потом будут гореть в геенне огенной. Поэтому способности объяснять вещи, или хотя бы намекать на их суть у них не было, в общем, как умения делать вещи простые. Майя сделали постапокалиптический календарь, вызвавший много мух из слона и мыслей о жизни в среднестатистического человека, а египтяне древние построили пирамиды, предназначение которых волнует даже художников. А раз так, мы будем учится как рисовать пирамиды карандашом. Пирамиды Хеопса — одно из чудес света, куча булыжников, приносящих большой доход от наплыва туристов, а также архитектурный шедевр, построенный еще до нашей с вами эры. В давние времена, за правления бога солнца Ра, их использовали для погребения фараонов, жертвоприношения, платонических контактов с потусторонним миром и других массовых развлечений. Пирамидообразная конструкция как оказалось очень надежная постройка, поэтому подобные здания сооружались и в Месопотамии, Китае, Марсе и Лас Вегасе. Если верить точным источникам из википедии, то пирамиды в Египте называются египетскими, в Китае китайскими и так дальше. Ну вы поняли.

Одно я знаю наверняка, рисовать мистические сооружения куда проще, чем строить, тем более, если делать это по таким шагам:

Как нарисовать пирамиду карандашом поэтапно

Шаг первый. Нарисуйте несколько треугольников, желательно, ровных, а снизу будет песочный фон с верблюдами. Пока что обозначим их окружностями.

Шаг второй. Аккуратно выделите формы пирамид, обведите контуры.
Шаг третий. Теперь добавим несколько бедуинов с верблюдами.
Шаг четвертый. Добавим немного штрихов для правдоподобности. Можно даже раскрасить цветными карандашами. Но это уже оставляю Вам:
Попробуйте нарисовать еще и другие загадочные места нашей планеты.

В этом уроке создадим рисунок пирамиды. Эта фигура из разряда легких, пожалуй, легче чем куб. Если вы внимательно прочитали , то этот урок для вас будет больше повторение пройденного материала. Еще раз хочу повторить, что изобразительное искусство начинается с , или пером, или ручкой… и с натуры.

Здесь мы просмотрим больше схематическое создание пирамиды, чем художественное. Вообще наши уроки больше схемы рису

fashionlife33.ru

Как сделать тетраэдр 🚩 Тетраэдр из бумаги 🚩 Математика

Причин создать пирамиду дома из бумаги достаточно много. Во-первых, это достаточно красивое и оригинальное решение для декора квартиры, особенно, если подойти творчески к оформлению наружной ее поверхности. Во-вторых, пирамида Золотого сечения (к таким относится и пирамида Хеопса), по утверждениям многих исследователей обладает удивительными свойствами: улучшает самочувствие, настроение, заряжает воду. В некоторых исследованиях даже пытались доказать, что находясь в пирамиде, продукты портятся значительно медленнее, чем вне нее.

Что нужно, чтобы сделать пирамиду из бумаги

Сделать пирамиду из бумаги достаточно просто, для этого необходимо подготовить лист ватмана форматом А0 (610 мм x 863 мм), ножницы, и клей.

Для начала следует сделать чертеж на ватмане. Из листа такого размера получится пирамида высотой примерно 50 см.

1. Расположите лист в горизонтальном положении.


2. Проведите вертикальную линию посередине листа, отступив на 2–3 см от верха, длиной 52,5 см. Это будет одно из ребер пирамиды, от которого будет выстроен дальнейший чертеж.


3. Проведите окружность с радиусом, равным длине ребра, центром окружности будет верхняя точка первого отрезка.


4. От нижней точки первого отрезка отложите вправо и влево по две хорды длиной 23,4 см.


5. Соедините полученные хорды с верхней точкой первого отрезка – это будут остальные ребра пирамиды.


6. Справа или слева от последнего ребра проведите параллельную ребру линию, это будет припуск на склеивание пирамиды.


7. Аккуратно вырежьте полученную фигуру и согните ее по граням. Чтобы грани получились ровные и острые, проведите по сгибу заостренным предметом несколько раз в одну и другую сторону.


8. Склеивайте пирамиду по припуску, используя резиновый клей или ПВА, главное условие – чтобы клей не стягивал бумагу после высыхания.

Итак, ваша пирамида готова!

 

www.kakprosto.ru

10 класс. Геометрия. Тетраэдр. Задачи на построение сечений в тетраэдре. — Тетраэдр. Задачи на построение сечений в тетраэдре.

Комментарии преподавателя

Как построить тетраэдр? Возьмем произвольный треугольник АВС. Произвольную точку D, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.

Рис. 1. Тетраэдр АВСD

Элементы тетраэдра
А, B, C, D – вершины тетраэдра.
AB, AC, AD, BC, BD, CD — ребра тетраэдра.
ABC, ABD, BDC, ADC — грани тетраэдра.

Замечание: можно принять плоскость АВС за основание тетраэдра, и тогда точка 

D является вершиной тетраэдра. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ – это пересечение плоскостей АВD и АВС. Каждая вершина тетраэдра – это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС, АВD, АDС. Точка А – это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВD ∩ АСD. 

Тетраэдр определение

Итак, тетраэдр — это поверхность, образованная четырмя треугольниками.

Ребро тетраэдра — линия перечесения двух плоскостей тетраэдра.

Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.

Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит ребру тетраэдра ВD и точка Р принадлежит ребру DС (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP.

Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью

Решение: 
Рассмотрим грань тетраэдра DВС. В этой грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP – это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е (Рис. 3.).

Рис. 3. Рисуно

www.kursoteka.ru

Лекция по математике на тему «Тетраэдр»

Лекция по теме «Тетраэдр»

Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».

Кристаллическая решетка метана

Тетрапакет для молока

Любимая игрушка моего детства Кубик Рубика

Уголковый отражатель

Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.

текст

Многоугольник- часть плоскости, ограниченная замкнутой линией без самопересечений, включая ее саму.

Необходим вот такой рисунок с пояснениями или чертеж треугольника.

Картинка

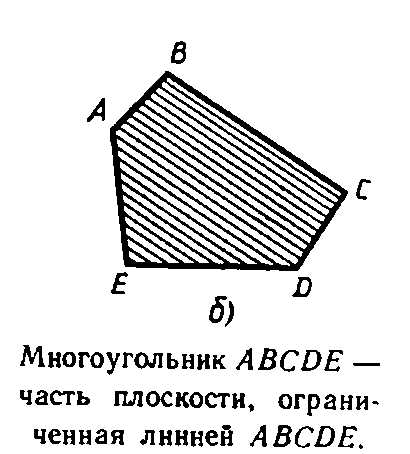
А именно о тетраэдре.

Нужна анимационная картинка тетраэдра, которая вращается, грани раскрашены в разные оттенки зеленого цвета.

ТЕТРА́ЭДР [фр. tétraèdre < греч. tetra четыре + hedra сторона, основание]. геом. Четырехгранник, треугольная пирамида.

(пауза)

Проводить изучение многогранников будем по плану:

1. определение тетраэдра

2. элементы тетраэдра

3. развертка тетраэдра

4. изображение на плоскости

План изучения многогранников:

1. определение тетраэдра

2. элементы тетраэдра

3. развертка тетраэдра

4. изображение на плоскости

1. построим треугольник АBC

2. точка D, не лежащая в плоскости этого треугольника

3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.

Пошагово появляется чертеж

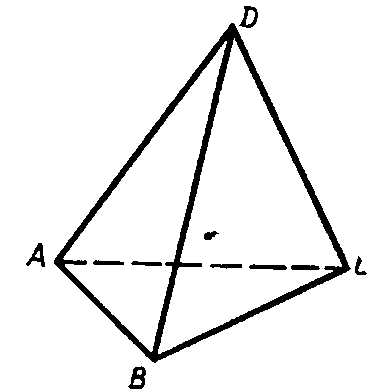
(пауза)

Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.

Обозначение: DABC.

Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.

Обозначение: DABC.

(Пауза)

Элементы тетраэдра

Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.

Сколько граней, ребер и вершин имеет тетраэдр?

Желательно чтобы появился предыдущий рисунок и элементы подписывались на чертеже и указывались стрелочками по мере их прочтения.

(пауза)

Тетраэдр имеет четыре грани, шесть ребер и четыре вершины

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.

На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB

Появляется предыдущий рисунок, по мере чтения текста цветом на рисунке выделяются противоположные вершины

Текст

противоположными ребра AD и BC, BD и AC, CD и AB

Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.

Развертка тетраэдра.

Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,

ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.

На экране появляется развертка тетраэдра.

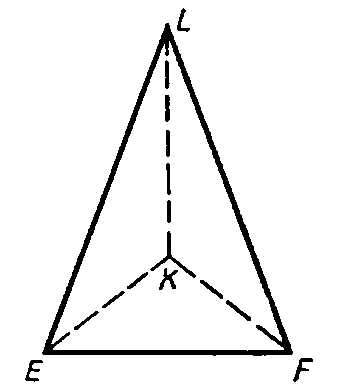
На плоскости тетраэдр изображается

В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.

На первом рисунке AC- невидимое ребро,

на втором – EK, LK и KF.

Изображение тетраэдра на плоскости:

Решим несколько типовых задач на тетраэдр:

Задача 1.

Найти площадь развертки правильного тетраэдра с ребром 5 см.

Решение. Начертим развертку тетраэдра

(на экране появляется развертка тетраэдра )

Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.

Площадь правильного треугольника ищем по формуле:

Задача 1. Найти площадь развертки правильного тетраэдра с ребром 5 см.

Площадь правильного треугольника:

Тогда получаем площадь тетраэдра равна:

Подставим в формулу длину ребра а=5 см,

получается

Ответ: Площадь развертки правильного тетраэдра

Площадь полной поверхности правильного тетраэдра

Задача 2

Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.

Задача 2

Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.

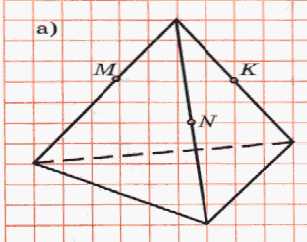
б)

а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.

а)

б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.

б) (Построение желательно делать поэтапно со словами диктора)

infourok.ru

Тетраэдр

Материал урока.

В начале изучения курса «Стереометрии» мы говорили, что все геометрические тела делятся на тела вращения и многогранники. В процессе изучения геометрии в десятом классе, мы будем подробно рассматривать с вами свойства тех или иных фигур.

Сегодня мы познакомимся с такой фигурой как тетраэдр. Прежде чем приступить к изучению пространственной фигуры, давайте вернемся в планиметрию и вспомним такую фигуру как многоугольник.

Напомню, что многоугольником называется либо замкнутая линия без самопересечений либо часть плоскости, ограниченная этой линией, включая ее саму.

Для стереометрии нам естественно подходит второе определение. Это определение показывает, что каждый многоугольник представляет собой плоскую поверхность.

Напомним, что простейшим многоугольником является треугольник. Возьмем треугольник ABC и точку D, которая не лежит в плоскости треугольника ABC. Соединим точку D с каждой вершиной треугольника ABC. Таким образом, мы получим три новых треугольника DAB, DBC, DCA. Тогда фигуру, которая состоит из четырех треугольников ABC, DAB, DBC, DCA, называют тетраэдром и обозначают так: DABC.

Треугольники, из которых состоит тетраэдр, называются гранями, стороны этих треугольников называют ребрами, вершины этих треугольников называются вершинами тетраэдра.

 Нетрудно посчитать, что тетраэдр имеет четыре грани, 6 ребер и четыре вершины. Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Давайте запишем пары противоположных ребер тетраэдра, который изображен на рисунке.

Это будут ребра AD и BC, BDи AC, CD и AB. Иногда одну из граней тетраэдра называют основанием, а три другие – боковыми гранями.

Слово тетраэдр произошло от древнегреческих слов теторес – четыре и эдра – основание или грань.

Если все грани тетраэдра – равносторонние треугольники, то такой тетраэдр называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями.

Последователи Пифагорейской философской школы форму тетраэдра придавали стихии огня.

Тетраэдр, все грани которого равные между собой треугольники, называется равногранным тетраэдром.

Если ребра тетраэдра, которые прилегают к одной вершине, перпендикулярны между собой, то такой тетраэдр называется прямоугольным.

Тетраэдры обычно изображаются в виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.

На этом рисунке невидимым является только ребро AC.

А на этом рисунке невидимыми являются ребра ЕК, KF, KL.

Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов.

Ярким примером тетраэдра является разработанное для Нового Орлеана «здание-город», которое возвышается на 360 метров, включает в себя 20000 квартир, суммарная жилая площадь которых 2040000 квадратных метров. Здание использует экологичное энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре помещаются коммерческие организации, три отеля, культурные объекты, школа, больницы и казино. И, учитывая место, под которое создавался проект, его немаловажная особенность — способность держаться на плаву.

Решим насколько задач.

Задача. Назовите все пары скрещивающихся рёбер тетраэдра . Сколько таких пар рёбер имеет тетраэдр?

Решение.

Напомним, что две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Нетрудно увидеть, что скрещивающимися будут ребра AB и СD, АC и BD, АD и BC. То есть в тетраэдре есть три пары скрещивающихся ребер.

Задача. В тетраэдре  , , , , , . Найти рёбра основания  данного тетраэдра.

Решение.

Задача. Пусть точки  и  – середины рёбер  и  тетраэдра . Доказать, что прямая  параллельна плоскости .

Доказательство.

Что и требовалось доказать.

Подведем итоги урока. Сегодня на уроке мы познакомились с пространственным многогранником – тетраэдром. Познакомились с элементами тетраэдра, решили несколько задач по данной теме.

videouroki.net

Как построить октаэдр 🚩 как начертить куб 🚩 Математика

12 марта 2012

Автор КакПросто!

Правильные многогранники были известны еще в Древней Греции. Они носят название «платоновых» тел. Четыре правильных многогранника – тетраэдр, икосаэдр, куб и октаэдр – олицетворяют четыре «сущности», стихии. Октаэдр символизирует воздух.

Статьи по теме:

Вам понадобится

• — бумага;
• — карандаш;
• — линейка.

Инструкция

Октаэдр состоит из восьми граней, являющихся правильными треугольниками. В правильном треугольнике все стороны равны между собой. Углы между сторонами такого треугольника составляют 60°. Высоты, медианы, биссектрисы совпадают. Для построения правильного октаэдра понадобится куб. Чтобы построить куб, начертите квадрат. Отступите некоторое расстояние вправо и вверх, постройте еще один такой же квадрат (левая и нижняя линии будут пунктирными). Соедините соответствующие парные точки обоих квадратов до визуализации куба. Поскольку на его основе вы будете строить октаэдр, сделайте его большим и четким.

Пусть дан куб. Необходимо построить октаэдр, вписанный в него. Проведите диагонали для каждой грани куба. Отметьте точки пересечения диагоналей. Соедините все полученные точки друг с другом. Правильный октаэдр, вписанный в куб, готов.

Для доказательства, что полученная фигура – правильный октаэдр, необходимо доказать правильность треугольников. Чтобы доказать, что треугольники-грани – правильные, проведите перпендикуляры от их вершин к ребрам куба. Используйте свойства прямоугольных треугольников и куба.

Можно также построить октаэдр, описанный около заданного куба. Пусть a – длина ребра куба. Найдите центры каждой грани (это точки пересечения диагоналей). Проведите прямые через центры противоположных граней. Они пересекутся в центре куба, который можно обозначить за точку О.

Итак, имеются две прямые, пересекающиеся в точке О. Отложите на каждой из прямых по обе стороны отрезок, равный 3a/2. Соедините концы полученных вами отрезков. Это и будет каркас правильного октаэдра, описанного около куба.

Полезный совет

Линии, которые не видны, должны быть пунктирными. Если вы сомневаетесь, виден ли тот или иной отрезок, лучше постройте пунктирный. Доделать пунктир до сплошной полосы легче, чем исправить сплошную линию на пунктир.

Додекаэдром называется правильный многогранник, грани которого представляют собой двенадцать правильных пятиугольников. Простейшим для построения правильным многогранником является гексаэдр или куб, все остальные многогранники можно построить, вписав или описав их около него. Додекаэдр можно построить, описав его около куба.

Видео по теме

Многогранник, у которого каждая грань представляет собой правильный многоугольник, т.е. многоугольник с равными сторонами, называется правильным многогранником. Всего существует пять правильных многогранников – тетраэдр, октаэдр, икосаэдр, гексаэдр(куб) и додекаэдр. Самым простым в построении является гексаэдр. Любой другой правильный многогранник можно построить, описав его около куба или вписав его в куб.

Инструкция

Рассмотрим построение правильного многогранника на примере октаэдра.
Октаэдром называется правильный многогранник, состоящий из восьми граней, каждая из которых представляет собой правильный треугольник.
Построение октаэдра, вписанного в куб.
Построим куб. Проведём диагонали AC, BD, AF и DE и обозначим точки их пересечения O и P.

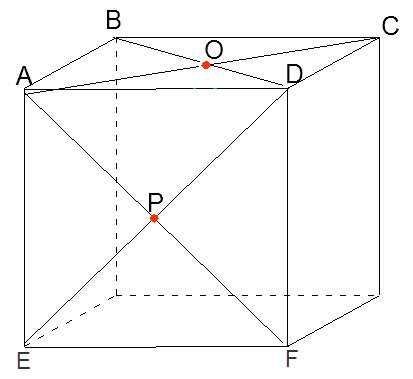
Соединив точки O и P, получим одно из рёбер строящегося октаэдра.

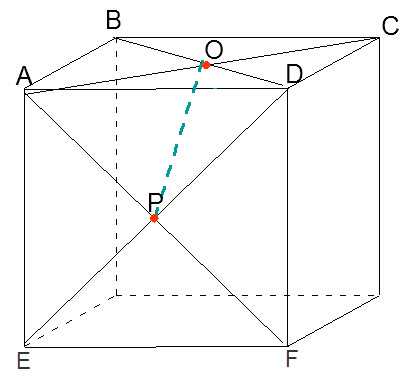
Повторив построения 1 и 2 для каждой грани куба получим октаэдр, вписанный в куб.

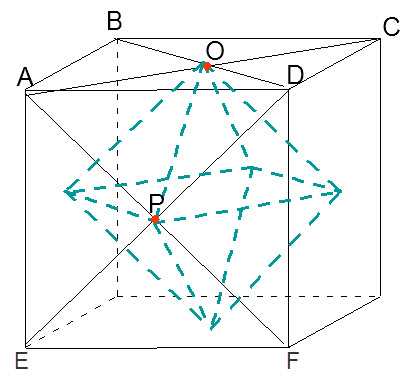
Построение октаэдра, описанного около куба.
Построим куб, через центры противолежащих граней проведём прямые. Эти прямые пересекутся в точке O – центре куба.

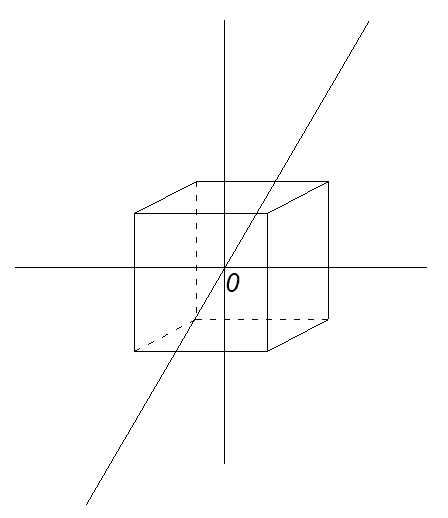
На проведённых прямых отложим отрезки так, чтобы точка O была их серединой. Длина отрезков будет равна 3 * a/2, где a — длина ребра куба.

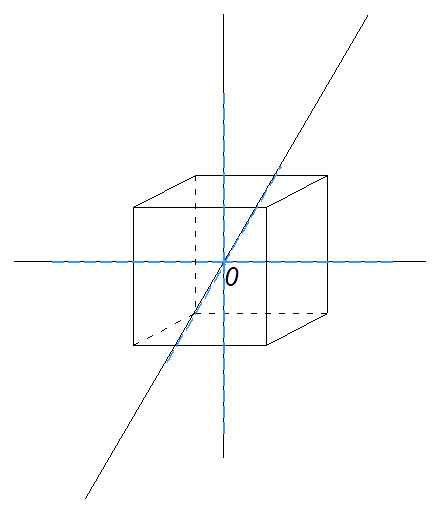
Соединив концы построенных отрезков, получим октаэдр, описанный около куба.

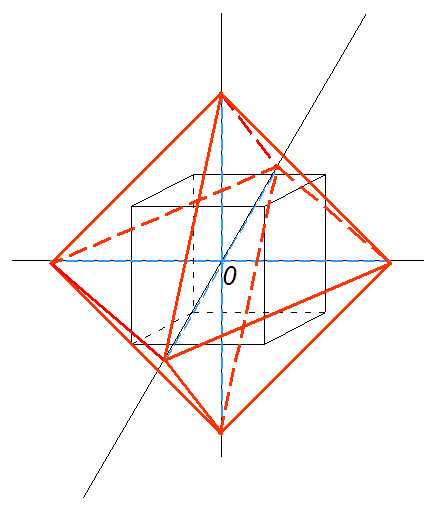
Видео по теме

Додекаэдр – это многогранная геометрическая фигура, которая состоит из двенадцати пятиугольников. Каждые три пятиугольника образуют одну из вершин этой замысловатой фигуры. Сегодня довольно часто используют додекаэдр при изготовлении различных сувениров и календарей.

Вам понадобится

• — макет додекаэдра;
• — ножницы;
• — линейка;
• — клей;
• — маркер;
• — картон;
• — карандаш;
• — бумага;
• — скрепки.

Инструкция

Купите готовые макеты календарей, имеющие форму додекаэдра, и соберите их. Получить такую фигуру несложно. Аккуратно вырежьте формы по намеченным границам. Затем при помощи линейки сложите додекаэдр в местах его сгиба (они изображены пунктиром) и склейте. Всевозможные потертости и небольшие визуальные дефекты замаскируйте с помощью маркера соответствующего цвета.

Смастерите додекаэдр. Для начала сложите ватман пополам с легким косым уклоном. На одной части картона нарисуйте в середине пятиугольник, а после от каждой грани нарисуйте еще по пятиугольнику. В итоге получится шесть нарисованных пятиугольников. Переколите ваш шедевр на вторую часть ватмана и нарисуйте точно такую же фигуру. Затем обозначьте места склейки. Когда основная работа будет завершена, вырежьте макет, разукрасьте и склейте его.

Приобретите тридцать листов бумаги (для красоты можно использовать бумагу трех цветов). Возьмите три листа бумаги и сделайте из них модули. Для этого сложите лист пополам, после чего каждую половинку еще раз пополам (в обратные стороны). То есть в итоге должен получиться веер. Заверните каждую сторону под прямым углом, а модуль немного наискосок. Отдельный модуль-трехлистник — вершина вашего додекаэдра. Продолжите конструирование из оставшихся двадцати семи листов. Лишь в конце сборки фигура станет устойчивой, поэтому во время творчества для большего удобства используйте скрепки.

Обратите внимание

Проверяйте качество склейки отдельных элементов додекаэдра!

Полезный совет

Из старых CD- дисков можно изготовить своими руками оригинальный подарок – светильник-додекаэдр, в котором один диск будет представлять отдельную грань фигуры. Для того чтобы собрать додекаэдр, наметьте на дисках линии пропилов, затем разрежьте их (ножовкой по металлу, раскаленной скрепкой или шилом) и сложите конструкцию.

Октаэдр – один из четырех правильных многогранников, которым люди придавали магическое значение еще в античные времена. Этот многогранник символизировал воздух. Демонстрационную модель октаэдра можно сделать из плотной бумаги или проволоки.

Вам понадобится

• — плотная бумага или картон;
• — линейка;
• — карандаш;
• — транспортир;
• — ножницы;
• — клей ПВА.

Инструкция

У октаэдра восемь граней, каждая из которых представляет собой равносторонний треугольник. В геометрии обычно строят октаэдр, вписанный в куб или описанный около него. Чтобы сделать модель этого геометрического тела, сложные расчеты не понадобятся. Октаэдр будет состоять из двух склеенных между собой одинаковых четырехгранных пирамид.

На листе бумаги начертите квадрат. На одной из его сторон постройте правильный треугольник, у которого все стороны равны, а каждый из углов составляет 60°. Треугольник удобно строить при помощи транспортира, отложив от двух прилегающих к одной и той же стороне углов квадрата по 60°. Через отметки проведите лучи. Точка из пересечения и будет третьим углом, а в дальнейшем – вершиной пирамиды. Такие же треугольники постройте на остальных сторонах квадрата.

Пирамиду вам придется склеивать. Для этого понадобятся припуски. Достаточно четырех припусков, по одному на каждый треугольник. Вырежьте то, что у вас получилось. Сделайте вторую такую же заготовку. Линии сгиба загните на изнаночную сторону.

Загните каждый из треугольников на изнаночную сторону. Припуски намажьте клеем ПВА. Склейте две одинаковые пирамидки и дайте им высохнуть.

Теперь нужно склеить пирамиды вместе. Намажьте квадратное дно одной из них клеем, прижмите дно второй, совместив стороны и углы. Дайте октаэдру просохнуть.

Чтобы сделать модель октаэдра из проволоки, вам понадобится картонный или деревянный квадрат. Впрочем, можно обойтись и обычным треугольником – чтобы согнуть заготовку под прямым углом, его вполне достаточно. Согните из проволоки квадрат. Отрежьте 4 одинаковых кусков проволоки размером в 2 стороны квадрата, плюс припуск на то, чтобы скрепить их в двух точках между собой, а при необходимости – прикрепить и к углам квадрата. Это зависит от проволоки. Если материал можно паять, длина граней равна удвоенной стороне квадрата без всяких припусков.

Найдите середину куска, примотайте или припаяйте его к углу квадрата. Таким же образом прикрепите остальные заготовки. Соедините находящиеся по одну сторону квадратного основания концы ребер между собой. Правильные треугольники получатся сами собой. Ту же операцию проделайте и с концами ребер, находящимися по другую сторону основания. Октаэдр готов.

Полезный совет

Проволоку для подобных моделей нужно выбирать такую, которая хорошо держит форму.

Источники:

• октаэдр как сделать

www.kakprosto.ru