Как нарисовать звезду карандашом (56 фото) — легкие мастер-классы по рисованию звезды
Главная » Полезные советы
Полезные советы0195
Звезда — одна из самых распространенных форм, которая адаптируется к любому виду бизнеса: рисованию, рукоделию, вышивке. Однако не всем удается нарисовать ровную звезду, как на картинке. Что делать, если вы хотите сделать подарочную карту своими руками? В этом случае есть четыре урока, которые могут помочь вам в работе.
Содержание:
- Звезда с компасом
- Звезда без компаса
- Детская версия звезды
- Звезда с тетрадными ячейками
- Фото-идеи и примеры рисования звезды
Содержание
- Звезда с помощью циркуля
- Звезда без использования циркуля
- Детский вариант звезды
- Звезда с помощью тетрадных клеток
- Фото идеи и примеры для рисования звезды
Звезда с помощью циркуля
С помощью привычных всем со школы циркуля нарисовать пятиконечную звезду довольно просто, тем более что для рисования понадобятся самые обычные вещи:
- бумага
- управлять.
- компас (механический или с карандашной вставкой)
Звездочка рисуется поэтапно:
- Укажите ось координат. То есть нарисуйте две линии, перпендикулярные друг другу.
- Поместите циркуль на пересечении линий и нарисуйте круг с радиусом, равным расстоянию от пересечения до края одной из линий.
- Поместите циркуль в любую из крайних точек пересечения основных линий. Чтобы определить радиус второй окружности, выберите точку на хорде немного дальше центра. Нарисуйте два круга по разные стороны от крайней точки.
- Укажите любую точку на оси пересечения. Соедините точку на верхнем поясе, точки пересечения главной оси и нижний пояс. Внутри четверти круга у вас должно быть еще две точки для дальнейшей работы. Соедините две точки внутри круга прямой линией.
- Повторите с другой стороны.
- Мысленно разделите свой круг на верхнюю и нижнюю половины, левую и правую, определите верхнюю часть звезд.
- От лука с помощью линейки проведите линию до точки, отмеченной циркулем на нижней правой струне.
- Из этой точки проведите линию, которая проходит через пересечение прямой из точки 4 и диаметра основной окружности.
- Проведите линию, параллельную диаметру круга. Он должен пересекаться с хордой вверху справа.
- Соедините его с точкой на хорде слева внизу.
- Завершите рисунок звезды, соединив прямую линию вверху.
Звезда без использования циркуля
Компас позволяет нарисовать ровно одну звездочку. Но что делать, если у вас под рукой нет компаса? Или просто лень? Также можно нарисовать прямую фигуру карандашом с линейкой.
- Заранее выберите, какой будет размер звезды — от этого зависит длина каймы.
- Основа рисунка — две параллельные линии на расстоянии, равном размеру границы (вы определяете ее сами), деленному на 1,55. Например, если длина 7 сантиметров, расстояние между линиями равно 4,5.
- Проведите вертикальную линию, перпендикулярную двум предыдущим и проходящую через их центры.
- Работаем с линией верха: отводим от центра количество сантиметров, равное выбранной длине стороны (7), делим пополам — в нашем случае это 3,5 сантиметра. Ставим точки по обе стороны от центра.
- По нижней строчке выполняем тот же узор, затем длину стороны (7) делим на три — получаем расстояние 2,3 сантиметра.
- Построим последний пункт: навершие. Для этого длину стороны (7) разбейте на 2,6 — расстояние будет 2,7 сантиметра.
- Соедините получившиеся точки и звезда готова!
Например, если длина 7 сантиметров, расстояние между линиями равно 4,5.Детский вариант звезды
Здесь больше не требуется детальная точность при выполнении. Работа над поделкой с детьми — это, прежде всего, возможность вместе весело провести время, поэтому трудностей возникнуть не должно.
Материалы потребуются те же: бумага, карандаши (можно и цветные), ластик
Размер звездочки выбирайте сами.
- Сначала проведите вертикальную линию. Вы можете стереть его позже, поэтому не нажимайте на карандаш слишком сильно.
- Определите центр линии и проведите два луча с одинаковым углом вверху, а затем внизу. Это «каркас» звезды.
Самое сложное позади! Теперь осталось только соединить полученные точки, но это тоже можно сделать оригинальным способом.
- Соедините получившиеся точки плавными непрямыми линиями — пусть края вашей звезды будут выпуклыми.
- Звезда завершена, но, пофантазировав, можно придумать лицо с глазами, носом, ртом, ресницами. Все зависит только от вашей фантазии.
- Последний шаг — раскрашивание. Помимо карандашей можно использовать краски, блестки и любые другие материалы.
Звезда с помощью тетрадных клеток
Идеально для тех, кто хочет скрасить скучное занятие или долгую беседу по телефону.
Главное в этой картинке — не запутаться в клетках.
- Обведите клетку в любом месте в центре листа — это будет верхушка.
- Обведите ячейку внизу справа и надрыв вверху.
- Затем сделайте шаг назад еще на одну ячейку вниз и вправо / влево и обведите две ячейки.
- Повторите шаг 3.
- Теперь спускайтесь на одну клетку вниз, но уже обведите клетки не снизу, а сбоку — это края звезды. Их длина составляет четыре-пять ячеек.
- Затем обведите ячейку по диагонали, двигаясь вниз и вправо / влево соответственно. Вы будете знать, когда остановиться.
- Определите две нижние точки звезды и нарисуйте клетки в любом количестве.
- Последнее, что осталось, это подключить. Вы можете использовать одиночные квадраты или обвести две ячейки.
Звезда готова.
Количество квадратов, размер звезды зависит только от вашего желания. Нарисовав саму рамку, можно приступать к раскрашиванию по клеточкам или придумывать рожицы звезде. С помощью цветных карандашей простой рисунок можно превратить в веселый образ.
Фото идеи и примеры для рисования звезды
Рейтинг
( Пока оценок нет )
admin/ автор статьи
Поделиться:Загрузка …
- Как вязать мотив спицами и крючком — описание схем вязания для начинающих
- Как вязать кардиган — описание схемы вязания крючком и спицами для начинающих
- Как упаковать подарок в подарочную бумагу — 62 фото идеи оригинальных украшений подарочных упаковок
Как нарисовать звезду (и не только) в полярных координатах / Хабр
Вопрос о формуле для многоугольника в полярных координатах регулярно возникает на тематических ресурсах — и так же регулярно остаётся без внятного ответа.
В лучшем случае попадается решение через функцию остатка от деления — что не является «чистым» с математической точки зрения, поскольку не позволяет производить над функцией аналитические преобразования. Видимо, настоящие математики слишком заняты решением проблем тысячелетия и поисками простого доказательства теоремы Ферма, чтобы обращать внимание на подобные банальные задачи. К счастью, в этом вопросе воображение важнее знания, и для решения этой задачи не нужно быть профессором топологических наук — достаточно знания школьного уровня.
Формула для равностороннего многоугольника в полярных координатах выглядит очень просто
и имеет следующие параметры:
— угол;
— количество выпуклых вершин;
— определяет, через какое количество вершин стороны будут лежать на одной прямой. Для него допустимы и отрицательные значения — от знака будет зависеть, в какую сторону будет выгибаться звезда;
— жёсткость — при мы получим окружность вне зависимости от прочих параметров, при — многоугольник с прямыми линиями, при промежуточных значениях от до — промежуточные фигуры между окружностью и многоугольником.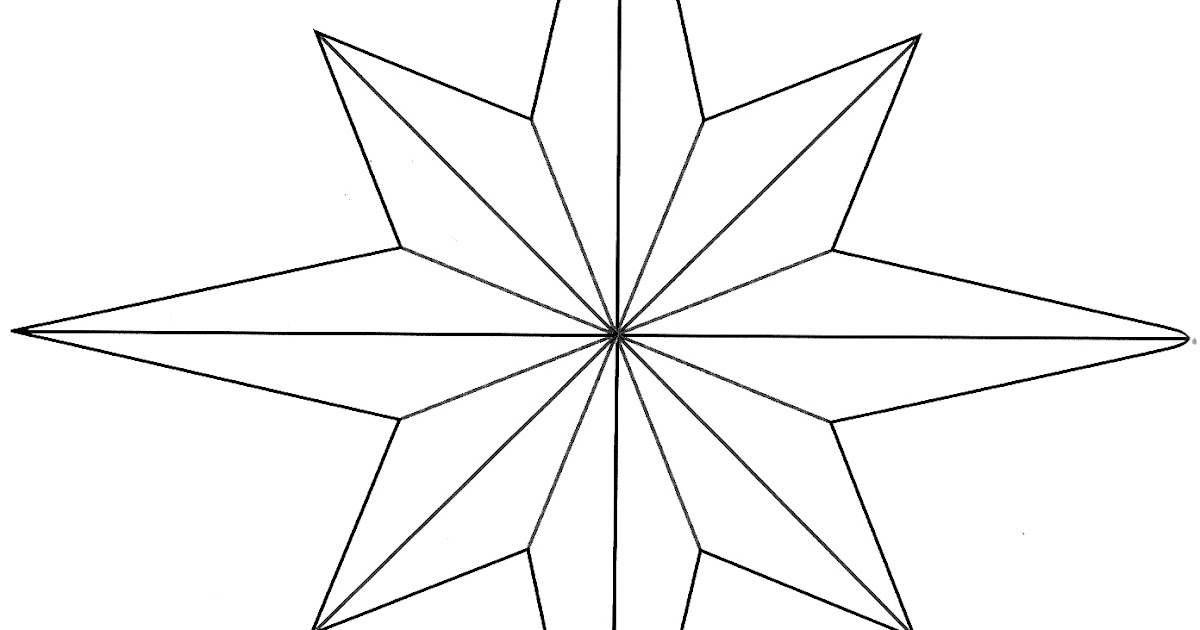
С этой формулой можно нарисовать звезду двумя путями:
1)
2) . В этом случае требуется сделать два оборота вместо одного:
Параметр влияет на многоугольник следующим образом (здесь он изменяется от -1 до 5):
Параметр в анимации:
Комплексная форма и модификации
Можно переписать исходную формулу в комплексном виде, и, несмотря на наличие в ней мнимых единиц, значение радиуса по-прежнему будет оставаться действительным:
На первый взгляд это может показаться бессмысленным, поскольку формула стала чуть более громоздкой — но не стоит спешить с выводами. Во-первых, в ней отсутствует арксинус, что полностью меняет математический смысл формулы и позволяет по-другому посмотреть на построение звёздчатого многоугольника. Во-вторых, из неё также можно получить компактные формулы для частных случаев, например . В-третьих (и самое интересное), её можно творчески модифицировать и получать другие, неожиданные формы.
Как вы наверняка заметили, вращение вектора перестало быть равномерным — и именно из-за появления мнимой составляющей в радиусе.
Квадрокруги и прочее
У нашей формулы есть замечательный частный случай — квадрат, формулу для которого можно выписать как
или
(выбирайте, какая больше нравится).
В чуть более развёрнутом случае можно определить промежуточные фигуры между кругом и квадратом через точку на плоскости
Можно также добавить вариативности этим фигурам с сохранением условия прохождения их через точку — модулируя непосредственно сам параметр в зависимости от угла таким образом, чтобы при прохождении через диагонали его множитель был равен единице.
Например, подставив вместо функцию , мы получим дополнительный параметр , которым можно регулировать дополнительные изгибы. В частности, для получится следующее:
В ещё более развёрнутом случае можно определить не просто квадрат — а прямоугольник, и по прежнему в полярных координатах:
И даже посчитать его площадь (через эллиптические интегралы):
Примечание
Для крайних значений ( и ) эта функция имеет особые точки, которые можно посчитать через предел и они ожидаемо будут равны и .
Это позволит делать профили с переходом из окружности в прямоугольник с контролируемой площадью сечения. Здесь площадь константна:
А здесь площадь расширяется по экспоненциальному закону:
Переход к декартовым координатам
Любую формулу в полярных координатах можно выразить через уравнение в декартовых координатах, причём как минимум двумя способами — в зависимости от чего будет изменяться вид градиента на границе фигуры.
Для этого достаточно посчитать угол через арктангенс от координат и привести формулу к константе через радиус-вектор вычитанием
или делением
Второй вариант предпочтительнее, поскольку даёт прямые градиенты вдоль сторон многоугольника.
Примечание
Здесь также нужно помнить, что в точке (0,0) возникает неопределенность из-за деления на ноль — которая, впрочем, легко разрешается через предел (который будет равным в первом случае и нулю во втором).
Выражение также можно упростить до , коэффициенты числителя которого при разложении образуют знакочередующий вариант последовательности A034839.
Значение формулы из правой части уравнения (во 2-м случае) будет меняться от до если точка попадает внутрь фигуры, и от до бесконечности — если нет. Выбирая различные функции для преобразования её в яркость, можно получать различные варианты растеризации.
Для экспоненты ( для первого и для второго варианта) получим
или, если с насыщением
Можно использовать классический фильтр нижних частот , в котором — порядок фильтра, определяющий степень затухания.
Для первого варианта:
И для второго:
Можно использовать и кусочно-непрерывную функцию, явно задавая границы интерполяции.
Помимо растеризации как таковой, можно задавать и деформации — например, сжать шахматную доску в круг:
Или даже натянуть её на сферу:
Формула
Классический стиль повествования в математических текстах состоит из чередования лемм/теорем и их доказательств — как если бы доказуемые утверждения появлялись у авторов в голове откровением свыше. И хотя в этом и бывает доля истины, чаще появлению формул предшествует некоторая исследовательская работа, описание которой может дать большее понимание их смысла, чем формальное доказательство; а верность утверждений, в свою очередь, можно проследить через верность шагов, к ним приведших.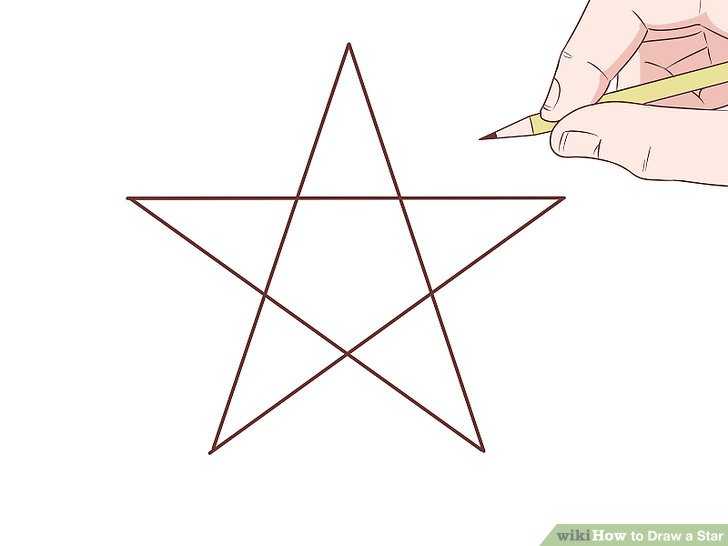
Так и здесь — если бы статья началась с формулы в комплексной форме, то её появление было бы неочевидным и контр-интуитивным, а заявленные свойства требовали бы дополнительных доказательств. Но в тригонометрической форме записи историю её появления вполне возможно проследить.
1) начинаем с самого простого случая — задаче начертить прямую в полярных координатах. Для этого нужно решить уравнение , решение которого очевидно .
2) далее аргумент секанса нужно «зациклить», чтобы обеспечить изломы в прямой. Именно на этом этапе другие решения используют «грязный хак» в виде остатка от деления. Здесь же используется последовательное взятие прямой и обратной функции синуса —
Такой подход позволяет производить стандартные математические операции над получившейся формулой,
например
можно её продифференцировать и получить функцию для прямоугольной волны:
Благодаря этой же записи можно упростить функцию квадрата в полярных координатах до более эстетического вида, используя представление тригонометрический функций в комплексном виде.
2))] /. \[Phi] -> ArcTan[x, y]
// TrigToExp // Simplify
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} &
// TrigToExp // Simplify // FullSimplify
↓
Заключение
Как видите, даже в такой простой и банальной вещи как многоугольник, можно найти и придумать что-то новое. И на этом история не заканчивается — осталась неизвестной формула площади для общего случая, осталась неизвестной формула для произвольного, а не только правильного многоугольника, остались без рассмотрения разложения в степенные и тригонометрические ряды. Также, вероятно, подобного рода формула существует и для 3-мерного случая.
Поэтому если вам говорят, что в математике уже всё придумано и остались лишь задачи недоступные пониманию обычного человека — не верьте. Есть много сугубо практических задач, о существовании которых настоящие математики не подозревают, или их решение им не интересно из-за отсутствия достаточного хайпа вокруг них, или потому что у них уже есть примерное представление путей достижения для их решения.
Не бойтесь браться за задачи, решение которых отсутствует в википедии, не бойтесь публиковать их решения и не бойтесь читать комментарии под статьями о бесполезности всего сущего.
P.S. скачать оригинальный документ для Mathematica можно здесь.
Как рисовать мультяшных звезд
122 акции
Узнайте, как нарисовать красивую мультяшную звезду , и пошаговые инструкции по рисованию, а также видео-учебник с простыми пошаговыми инструкциями.
Следуя простым шагам, вы тоже сможете легко нарисовать красивую мультяшную звезду.
Перейти к пошаговым инструкциям.
Полный рисунок мультяшной звездыУзнайте, как нарисовать милую мультяшную звезду, которую обычно можно увидеть на наклейках с наградами в классе.
Кто не любит звезды? Они волшебные, чудесные и напоминают о мерцающих ночах и далеких землях.
Когда вы видите звезду, вы обычно можете поспорить, что происходит что-то великое или даже волшебное.
Этот супер-милый урок покажет вам, как нарисовать очаровательную звезду за 10 простых шагов.
Рисунок звезды состоит из пяти точек, которые почти похожи на руки и ноги. У него также большие глаза, маленький нос, счастливая улыбка и все такое!
Прокрутите вниз, чтобы загрузить PDF-файл этого руководства.
Хотите нарисовать милую звезду? Это простое пошаговое руководство по рисованию мультфильмов поможет вам в этом.
Все, что вам понадобится, это ручка, ручка, маркер или мелок и лист бумаги.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Падающая звезда, Невозможная звезда и Звезда.
Пошаговые инструкции по рисованию милой звезды
Как нарисовать красивую мультяшную звезду для детей, начинающих и взрослых. Шаг 1
1. Начните с рисования изогнутой линии. Это формирует вогнутые стороны двух рукавов звезды.
Легкий рисунок мультяшной звезды. Шаг 2
2.
Продолжайте рисовать изогнутую линию, завершая одну из ветвей звезды.
Easy Cartoon Star Drawing — Шаг 3
3. Продолжайте рисовать изогнутую линию, завершая вторую руку.
Easy Cartoon Star Drawing — Step 4
4. Продолжайте рисовать изогнутую линию, завершая третью из пяти ветвей.
Easy Cartoon Star Drawing — Шаг 5
5. Продолжайте рисовать изогнутую линию, завершая две оставшиеся руки и окружая фигуру. Теперь у вас есть контур пятиконечной звезды.
Easy Cartoon Star Drawing — Step 6
6. Чтобы сделать звезду милой и мультяшной, мы добавим черты лица.
Нарисуйте две короткие толстые изогнутые линии внутри звезды. Они образуют брови звезды.
Easy Cartoon Star Drawing – Шаг 7
7. Вложите несколько кругов меньшего размера один в другой, чтобы получились глаза. Заштрихуйте второй по величине, указав на зрачок.
Добавьте больше деталей к изображению мультяшной звезды — шаг 8
8. Нарисуйте почти полный круг, чтобы сформировать нос звезды.
Завершите контур вашего рисунка мультяшной звезды – Шаг 9
9. Нарисуйте широкую U-образную линию, чтобы сформировать улыбающийся рот звезды. Нарисуйте короткие изогнутые линии на каждом конце. Контур вашего милого звездного рисунка готов.
Раскрась свою мультяшную звезду
Раскрась свою звезду. В природе звезды могут казаться желтыми, оранжевыми, красными, белыми или даже синими. В мультяшном контексте они могут быть любого цвета, так что будьте изобретательны!
Вы можете найти больше забавных персонажей для рисования или заполнить небо дополнительными звездными объектами.
Дополнительные уроки по рисованию мультфильмов см. в посте «51 простая и забавная идея рисования мультфильмов».
Простое пошаговое руководство по рисованию мультяшной звездыНажмите ЗДЕСЬ, чтобы сохранить урок в Pinterest!
Учебное пособие по рисованию мультяшной звезды — легко и весело Страницы для печати
УСТРАНЕНИЕ НЕИСПРАВНОСТЕЙ ДЛЯ УЧАСТНИКОВ
Все еще видите рекламу или не можете загрузить PDF-файл?
Во-первых, убедитесь, что вы вошли в систему.
Вы можете войти на странице входа в систему.
Если вы по-прежнему не можете загрузить PDF-файл, вероятное решение — перезагрузить страницу.
Это можно сделать, нажав кнопку перезагрузки браузера.
Это значок в виде круглой стрелки в верхней части окна браузера, обычно расположенный в верхней левой части (вы также можете использовать сочетания клавиш: Ctrl+R на ПК и Command+R на Mac).
Рисование многоугольников и звезд | CorelDRAW
Рисование многоугольников и звезд
CorelDRAW позволяет рисовать многоугольники и два типа звезд: идеальные и сложные. Совершенные звезды — это звезды традиционного вида, к которым можно применить заливку по всей форме звезды. Сложные звезды имеют пересекающиеся стороны и дают оригинальные результаты с примененной заливкой.
Слева направо: многоугольник, идеальная звезда и сложная звезда, каждая с фонтанной заливкой
Вы можете изменять многоугольники и звезды. Например, вы можете изменить количество сторон многоугольника или количество вершин звезды, а также заострить вершины звезды.
Вы также можете использовать Shape Инструмент для изменения формы многоугольников и сложных звезд так же, как и для любого другого кривого объекта. Дополнительные сведения о работе с объектами кривых см. в разделе «Использование объектов кривых». Совершенные звезды также могут быть изменены, но с некоторыми ограничениями.
Чтобы нарисовать многоугольник |
• |
| В наборе инструментов щелкните инструмент Многоугольник и перетащите его в окне рисования, пока многоугольник не станет нужного размера. |
• |
| Вы можете нарисовать многоугольник из его центра, удерживая Shift при перетаскивании. |
• |
| Вы можете нарисовать симметричный многоугольник, удерживая Ctrl во время перетаскивания. |
Нарисовать звезду |
| от до | Сделайте следующее |
|---|---|
Нарисуй идеальную звезду | В наборе инструментов щелкните инструмент Star и перетащите его в окно рисования, пока звезда не станет нужного размера. |
Нарисовать сложную звезду | В наборе инструментов щелкните инструмент Сложная звезда и перетащите в окно рисования, пока звезда не станет нужного размера. |
• |
| Вы можете нарисовать звезду из ее центра, удерживая Shift при перетаскивании. |
• |
| Вы можете нарисовать симметричную звезду, удерживая Ctrl при перетаскивании. |
Чтобы изменить многоугольник |
| от до | Сделайте следующее |
|---|---|
Изменить количество сторон многоугольника | Выберите многоугольник, введите значение в поле Число точек или сторон многоугольника, звезды или сложной звезды на панели свойств и нажмите Введите . |
Преобразование многоугольника в звезду | Выберите многоугольник, нажмите кнопку Инструмент Форма и перетащите узел на многоугольнике, пока звезда не примет нужную форму. |
Слева направо: Инструмент Shape использовался для преобразования многоугольника в звезду, которой можно придать форму кривого объекта. Затем линейные сегменты звезды были преобразованы в кривые и скорректированы для получения формы морской звезды.
Для модификации звезды |
| от до | Сделайте следующее |
|---|---|
Изменить количество точек на звезде | Выберите звезду, введите значение в поле Количество точек или сторон многоугольника, звезды или сложной звезды на панели свойств и нажмите Введите . |
