Цилиндр. Виды, объём цилиндра, площадь поверхности :: SYL.ru
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
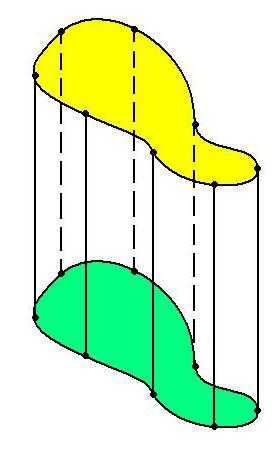
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.
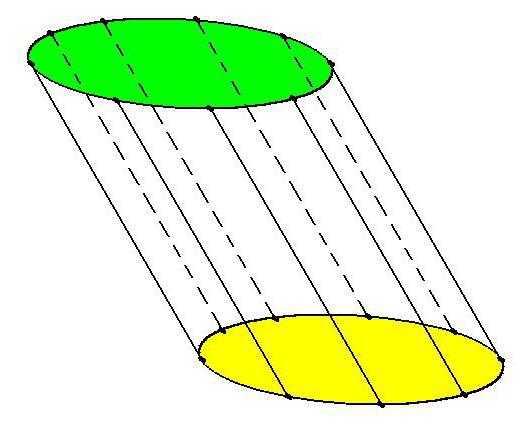
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
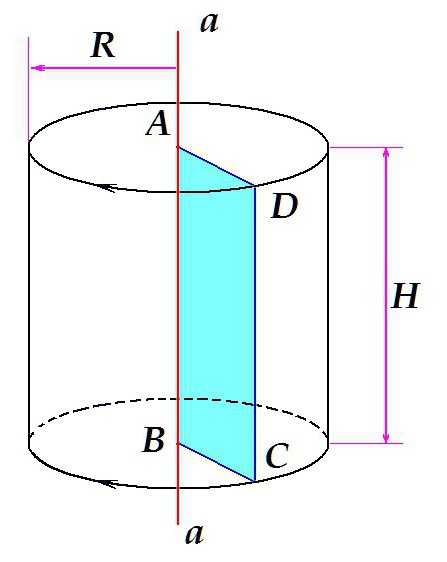
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
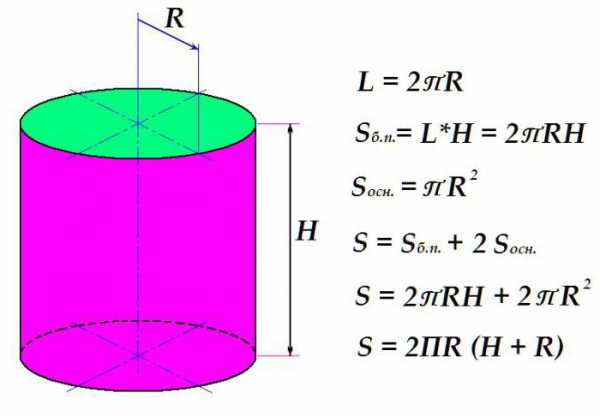
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
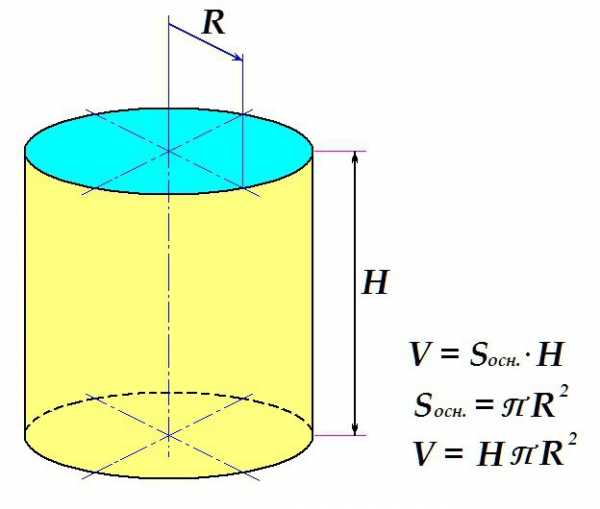
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
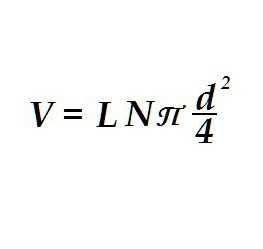
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
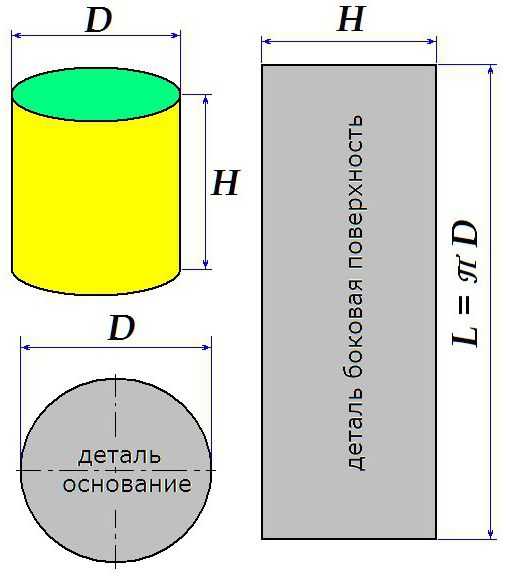
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
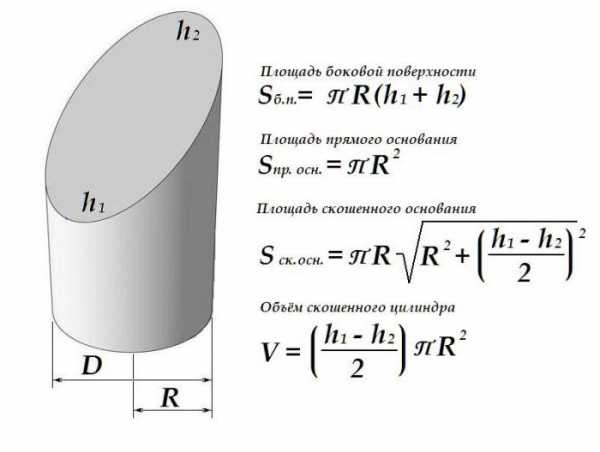
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
www.syl.ru
Цилиндр как геометрическая фигура
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.
На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О1 являются его основаниями.
Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.
Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
Sb = Ph.
В частности, для прямого кругового цилиндра:
P = 2πR, и Sb = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
Sp = 2πRh + 2πR2 = 2πR(h + R)
Для нахождения объёма наклонного цилиндра существуют две формулы.
Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):
V = Sh = S l sin α,
где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.
Формула для нахождения объёма кругового цилиндра выглядит следующим образом:
V = π R2 h = π (d2 / 4)h,
где d – диаметр основания.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Построение цилиндра в перспективе, вид сбоку — Урок 13.5
Положим один кирпич поверх другого. Предположим, что их торцы образуют квадрат. Нарисуем на торцах диагонали и тем самым найдем центр. Это центр круга, который касается всех четырех сторон квадрата.
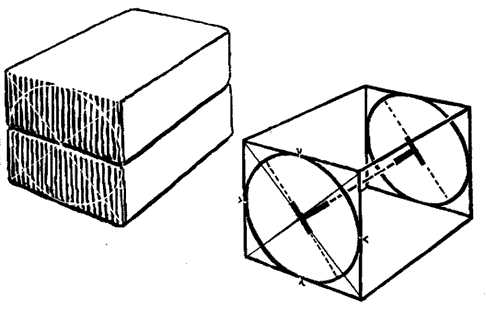
Рис 1. Построение цилиндра в черчении без перспективы
Этот круг можно расценивать как торец цилиндра, который проходит через всю толщу кирпича. На противоположном торце нарисуем еще один круг.
Линия, проведенная между центрами двух окружностей, — это центральная/осевая линия цилиндра или в нашем случае — ось двух колес. Эта ось — продолжение коротких осей двух эллипсов и ножка двух букв Т.
Длинная ось образует перекладину буквы Т.
Мы начали с предположения, что торцы двух кирпичей, положенных один на другой, образуют квадрат.
Теперь попробуем рисовать цилиндр в перспективе
Нарисуем кирпичи с применением законов перспективы. Круг, вписанный в квадрат, становится эллипсом, касающимся сторон квадрата (нарисованного в перспективе) в центре каждой из сторон.
Рис 2. Построение цилиндра в перспективе
Линия, проведенная через центр круга до точки схода, должна быть центральной линией цилиндра или осью для двух колес.
Большая ось всегда образует прямой угол с центральной осью цилиндра.
Нет никакой разницы, в каком направлении лежит цилиндр и лежит ли он на боку или стоит на торце, большая ось эллипса всегда будет образовывать букву Т с центральной/осевой линией цилиндра. Малая ось эллипса лежит вдоль этой центральной/осевой линии цилиндра. Малая ось эллипса становится центральной линией цилиндра, т.е. они должны совпадать.
Рис 3. Правильное положение осей эллипса цилиндра в пространстве
Нарисуйте/начертите цилиндр с соблюдением правил перспективы. Затем поверните бумагу так, чтобы цилиндр оказался в вертикальном положении.
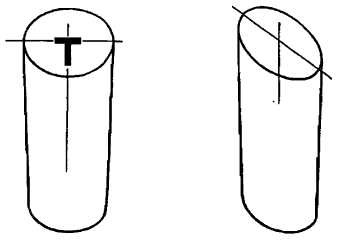
Рис 4. Цилиндр в перспективе в вертикальном положении
Первое изображение цилиндра является правильным, второе — неправильное.
risovatlegko.ru
Практическая работа № 2. Рисунок цилиндра и конуса в проекции
Практическая работа № 2. Рисунок цилиндра и конуса в перспективеЗадание № 1. Линейно-конструктивное построение геометрического тела — цилиндр. С частичной тоновой проработкой;
Задание № 2. Линейно-конструктивное построение геометрического тела — конус. С частичной тоновой проработкой.
Материал: простой карандаш различной твердости, акварельная бумага, ластик
Порядок выполнения:
Цилиндр — геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности. Форма цилиндра своеобразная. В отличие от куба свет по цилиндрической поверхности распределяется во многом сложнее. Основаниями цилиндра служат круглые плоскости, и если они находятся под каким-либо углом (в ракурсе), то выглядят уже эллипсами.
Последовательность рисования цилиндра:
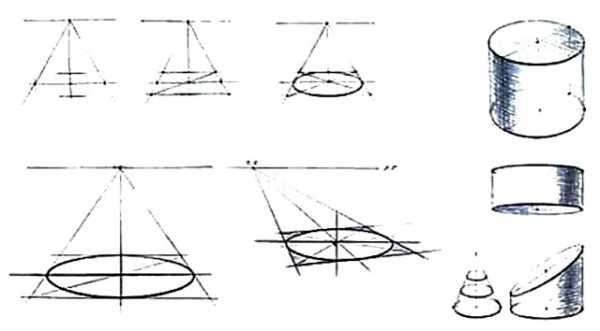
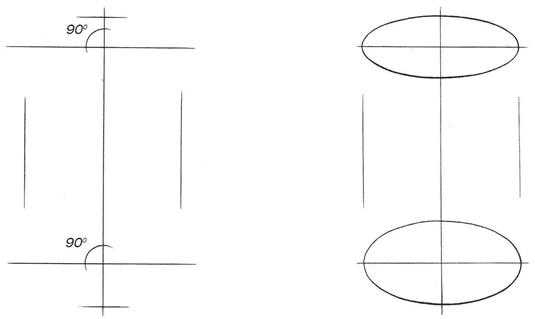
Первый этап. Определение размеров цилиндра, основных пропорций (высоты и ширины). Нахождение его расположения на листе. Построение осевых линий. Для этого определяется положение вертикальной оси цилиндра. Перпендикулярно к ней строятся осевые линии верхнего и нижнего оснований цилиндра.
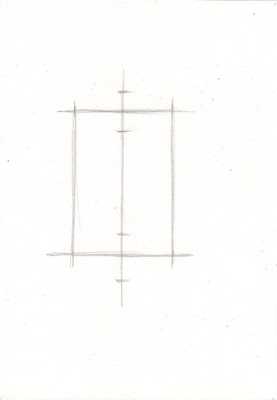
Второй этап. Прорисовка овалов, передающих перспективное сокращение верхнего и нижнего оснований цилиндра. Определение границ света и тени.
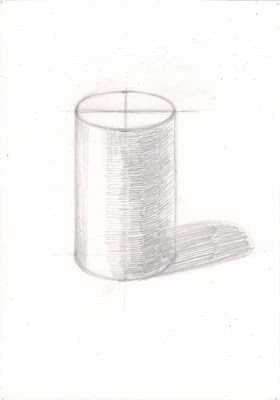
Третий этап. Нанесение светотени для выявления объема. Штрихи подчеркивают форму цилиндра. Обобщение и соблюдение верных тональных отношений в процессе завершения работы для достижения законченности рисунка. Построение цилиндра, расположенного вертикально, начните с компоновки общей формы тела. Чтобы не ошибиться в размещении общей формы (белого силуэта) цилиндра в вертикальном формате листа бумаги, проведите легкую вертикаль в середине и зрительно определите высоту изображаемого тела, а затем его ширину.Далее построение формы цилиндра оказывается действенным средством развития знаний и практических навыков в рисовании, так как помогает хорошо усвоить правила перспективы и конструктивного строения предметов. Выполняя данную работу, вы должны действовать уверенно, свободно держать карандаш.
Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей — вписыванием в квадрат.
Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра.
Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней. 
При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра — ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.
По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.
Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.
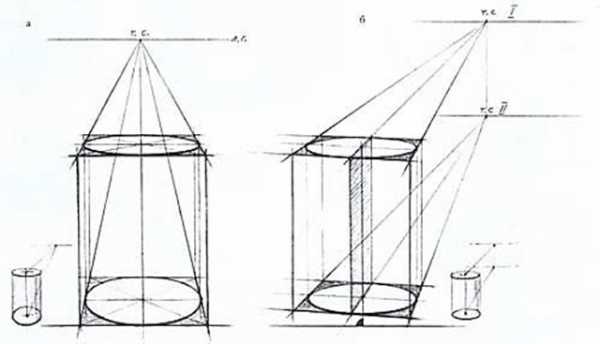
Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра. Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей. В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.
Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем — цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол между осью призмы и отрезком линии, которая и будет большой осью эллипса. Эта важная деталь, о ней следует всегда помнить студентам, является причиной грубых ошибок при изображении цилиндра в горизонтальном положении. При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.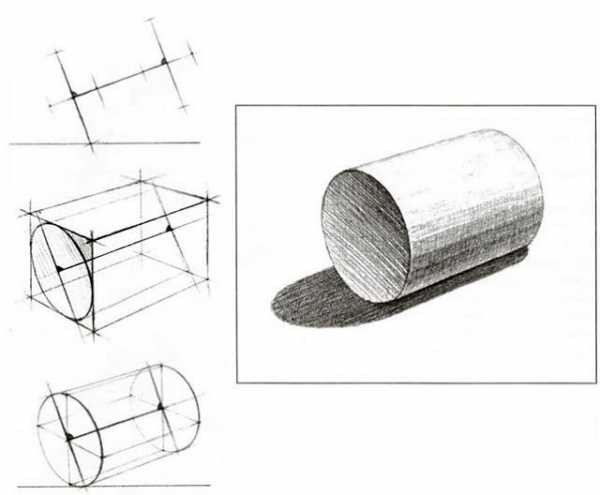
| Последовательность рисования цилиндра в горизонтальном положении |
Следует обратить внимание, что дальнее основание цилиндра по мере удаления от рисующего всегда несколько шире (по малой оси), чем переднее. Это обусловлено закономерностью перспективы.
Построив таким образом основания и дополнительно уточнив окружности (эллипсы), соединяют их образующими. В завершающей стадии построения изображения следует придать рисунку большую пространственность за счет усиления линий близлежащих и ослабления линий дальних форм.
Завершив построение, следует непременно его проверить. Внимательно проверив возможные ошибки, допущенные в процессе построения, и исправив их (если таковые имеются), следует перейти к длительному рисунку с помощью света, тени, полутени и рефлекса.
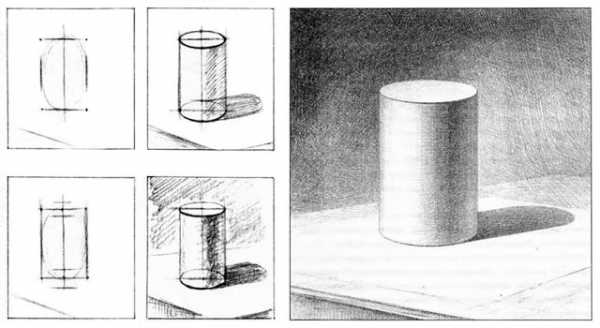
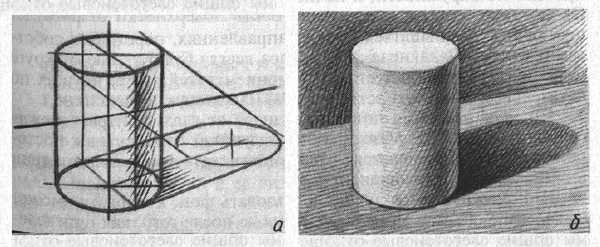
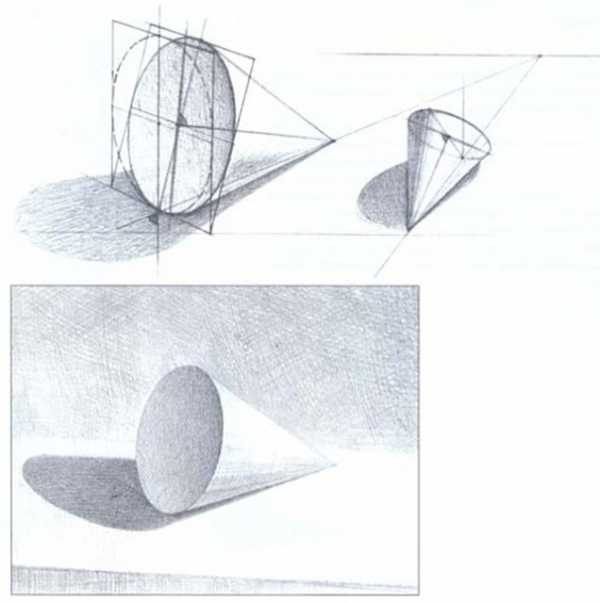
Принцип освещения очередной модели для рисования с натуры остается прежним. На этот раз вы будете выполнять тоновой рисунок цилиндра — геометрического тела, образованного вращением прямоугольной плоскости вокруг единой оси.
Построив каркас цилиндра, в котором верно изображены в перспективе оба основания (нижнее — немного шире, как это смотрелось в натуре), сравните изображение с натурой и переходите к моделировке формы тоном. Если в тоновом рисунке куба была определенная сложность, вызванная передачей пропорциональных натур светотеневых отношений, то в тональной характеристике цилиндра нужны дополнительные усилия, чтобы понять степень распределения градаций света и тени по его специфической поверхности.
Обязательно разберитесь в градациях, так как вместо передачи объемной формы нарисованное изображение может выглядеть словно помятым или сплющенным. Чтобы этого не произошло, будьте предельно внимательны в моделировке поверхности построенного на бумаге цилиндра.
Светотеневое решение формы цилиндра подчиняется знаниям рисующего. Каждый видит, как распространяющийся по округлой поверхности цилиндра свет четко строит форму геометрического тела. Наиболее ярко выглядит на цилиндрической поверхности небольшой участок. Это блик, и его явление вызвано тем, что на эту часть объема световые лучи попадают строго перпендикулярно. Далее свет начинает, как бы скользить по закругляющейся поверхности и, разумеется, ослабляет освещенность предмета, пока его воздействие не прерывается заходящей за границу между ним и тенью областью, становящейся самым темным пятном. Следовательно, цилиндрическая поверхность дает четкое зрительное представление последовательного распределения светотеневых градаций примерно в таком чередовании: полутон, свет, блик, свет, полутон, тень, рефлекс. Конечно, переходы между ними совершенно не различимы, и это одна из сложностей передачи в рисунке объемной формы цилиндра. Значит, вам необходимо не добиваться абсолютного сходства нарисованного цилиндра с натурой, а следить за верной передачей пропорциональных ей отношений градаций тона.
Фон в тоновом рисунке служит неотъемлемой частью
пространственного изображения. Кроме того, он влияет на общее состояние освещенности, оказываясь то нейтральным, то активно воздействующим на восприятие предмета.
Последовательность изображения вертикальностоящего цилиндра, расположенного ниже горизонта
Последовательность изображения горизонтального цилиндра,
расположенного ниже горизонта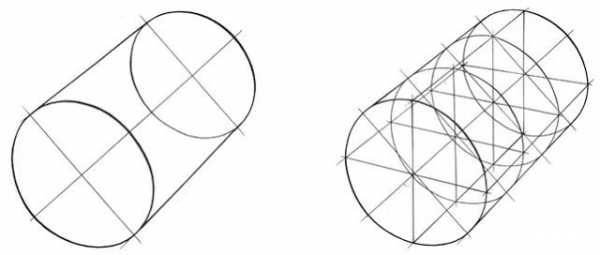
Определение тени
Рисование конуса
Конус определяется радиусом окружности основания и точкой вершины, поэтому при его построении, так же, как и при построении конструкции цилиндра, работу следует начинать с построения окружностей оснований в перспективном ракурсе.
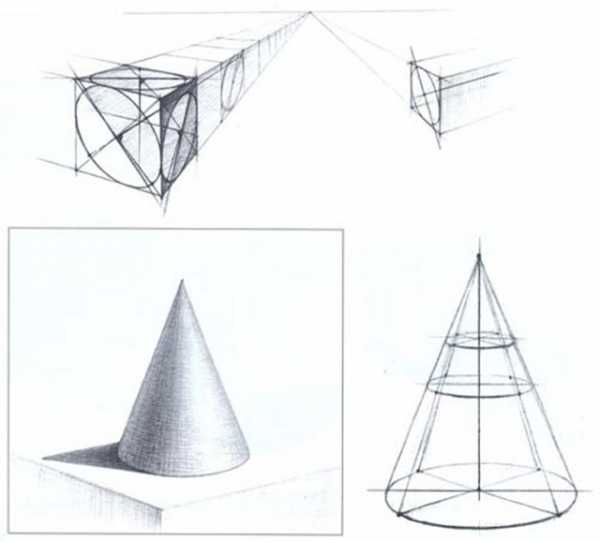
Построив окружность (эллипс) основания конуса, необходимо определить его вершину. Для чего от центра основания эллипса проводят вверх вертикальную линию — ось вращения, перпендикулярную к большой оси эллипса. Следует напомнить, что ось вращения и есть ось конуса, которая, независимо от положения в пространстве относительно угла зрения рисующего, всегда перпендикулярна к кругу основания конуса. Определив ось конуса с учетом его пропорции, отмечают точкой его вершину. После этого на окружности основания симметрично намечают пространственные точки образующей и соединяют их с точкой вершины конуса.
При изображении конуса в горизонтальном положении, независимо от угла поворота и ракурсов, следует исходить из того, что поверхность круга основания конуса всегда должна быть перпендикулярна оси вращения. Поэтому большую ось эллипса, вписанного в квадрат основания конуса, необходимо строить на линиях, проведенных под прямым углом к оси конуса. Касаясь построения усеченного конуса, нужно отметить, что он, как и цилиндр, определяется нижним и верхним основаниями и их взаимным расположением, лишь с той разницей, что диаметры этих оснований различны, а большие оси эллипса по отношению к оси конуса располагаются по-прежнему под прямым углом, за исключением случаев, когда секущая плоскость проходит под другими углами.
1. Рисунок цилиндра с тональным решением ,
2. Рисунок конуса с тональным решением
pedagogipt.blogspot.com
Цилиндр [wiki.eduVdom.com]
Цилиндром (прямым круговым цилиндром) называется тело, состоящее из двух кругов (оснований цилиндра), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Цилиндр является телом вращения.
Цилиндр
Рис.1
Вот другое определение:
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
Рис.1 мини
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр (просто цилиндр) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон.
См.Рис.1.
Радиус цилиндра – радиус его основания.
Образующая цилиндра — образующая цилиндрической поверхности.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Рис.2
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_{бок}=2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.
Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_{полн}=2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.
Объем всякого цилиндра равен произведению площади основания на высоту:
$$V = S\cdot h$$ Объем круглого цилиндра:
$$V=\pi r^2 \cdot h$$
, где (r — радиус основания).
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
wiki.eduvdom.com
Перспектива цилиндра в уроке рисунка на блоге «Иллюзион»
Давайте перейдем от перспективы куба к обзору — перспектива цилиндра, или скажем к фигуре цилиндрической формы. Это так же простое, не сложное задание.
Если рассмотреть мир вокруг нас — то эту форму имеют разные предметы это столб цилиндр, это труба цилиндр, это ваза цилиндр и даже шляпа цилиндр и т. д. А рисунок это умение строить, и тут уже не далеко и до гениальности, как написано в начале сайта.
Что бы правильно изобразить эту фигуру, нам необходимо будет вписать ее в прямоугольный параллелепипед.
Основа построения такая же, как и в уроке, перспектива куба.
Перспектива цилиндра
Вначале произвольно рисуем на листе линию горизонта, это прямая линия вдоль листа. Линия горизонта всегда находится на уровне глаз художника. На предметы выше этой линии художник смотрит снизу, на предметы ниже этой линии художник смотрит сверху. В данном уроке предмет у нас будет ниже линии горизонта, поэтому мы на него смотрим сверху. Все картинки кликабельны:
Дальше рисуем произвольно квадрат. В данном случае нарисуем фигуру ниже линии горизонта:
Потом на линии горизонта произвольно находим точку схода F , и луч соединяет углы нашего квадрата. Смотрим ниже:
Теперь прорисовываем квадрат сзади, и соединяем линиями углы заднего квадрата и переднего. Смотрим вниз:
Теперь необходимо найти центр верхней и нижней плоскости параллелепипеда. Для этого проводим новые линии с углов плоскостей, крест — накрест. В пересечении крестов будут центры плоскостей. Теперь прямая линия делит верхнюю и нижнюю плоскости пополам. Смотрим на нижнюю картинку:
Мы поделили параллелепипед вдоль. Необходимо поделить его поперек. Для этого проводим линию от точки схода F через центр плоскостей параллелепипеда.
Смотрим вниз:
Итак, мы нашли необходимые нам точки верхней плоскости A, B, C, D, и нижней плоскости цилиндра A1, B1, C1, D1.
Рисунок внизу:
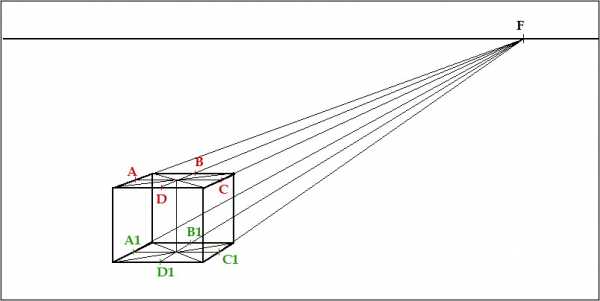
Теперь наша задача плавно вписать эллипс, соприкасаясь с точками верхней плоскости A, B, C, D .
Смотрим на рисунок ниже:
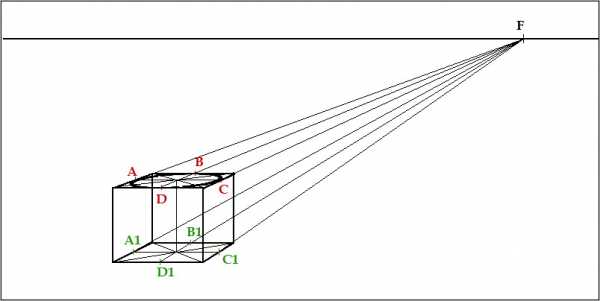
И так же поступаем с точками нижней плоскости цилиндра A1, B1, C1, D1. Таким образом мы очертим основание цилиндра :
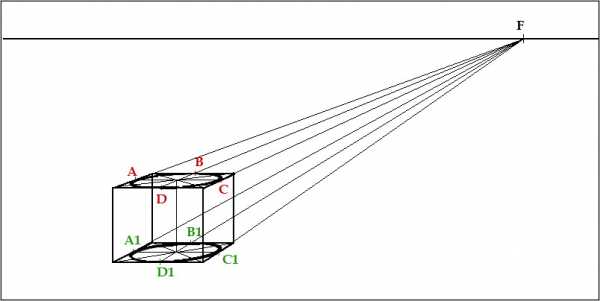
Теперь соединяем два эллипса, верхнее и нижнее основание цилиндра :
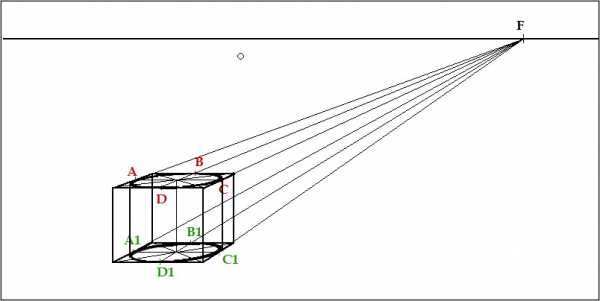
Убираем все вспомогательные линии, и получаем цилиндрическую форму :
Причем чем выше линия горизонта, тем плоскость эллипса будет больше и больше стремится к кругу. Или к форме — окружность.
artatac.ru
Цилиндр — урок. Геометрия, 11 класс.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Прямоугольник AOO1A1 вращается вокруг стороны OO1.
OO1 — ось симметрии цилиндра и высота цилиндра.
AA1 — образующая цилиндра, длина которой равна длине высоты цилиндра.
\(AO\) — радиус цилиндра.
Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра.
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается прямоугольник.
На рисунке изображён цилиндр, пересечённый плоскостью, которая параллельна оси цилиндра OO1.
ABB1A1 — прямоугольник.
\(OA = OB = R\) — радиусы.
\(OC\) — расстояние от оси цилиндра до плоскости сечения.
Дуга \(AB\) равна центральному углу \(AOB\).
При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.
Если представить, что боковая цилиндрическая поверхность разрезана по образующей AA1 и развёрнута, получаем прямоугольник.
Сторона AA1 равна высоте \(H\), а другую сторону образует развёрнутая окружность основания длиной 2πR.
Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:
Sбок.=2πR⋅H
Основания цилиндра — два круга с общей площадью 2⋅πR2.
Полная поверхность цилиндра определяется по формуле:
Sполн.=2πRH+2πR2=2πR⋅H+R
www.yaklass.ru