Построение звезды с помощью циркуля – Как нарисовать звезду циркулем 🚩 как рисовать знаменитостей 🚩 Математика

Нарисовать правильный пятиугольник онлайн вписанный в окружность

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

1. Циркуль
2. Карандаш
3. Линейка
4. Резинка

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

 

Как выглядит пятиугольник и звезда

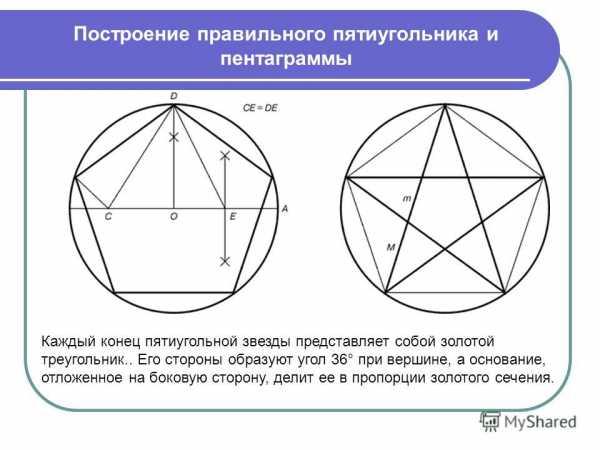
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

 

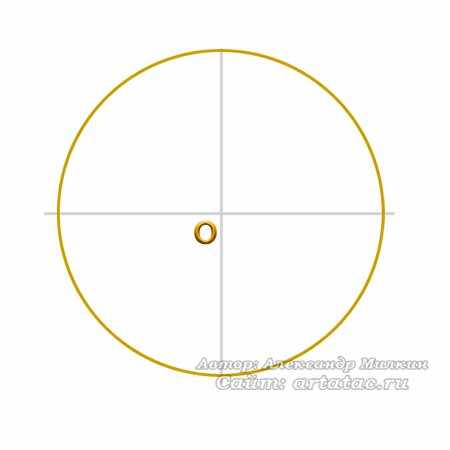
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

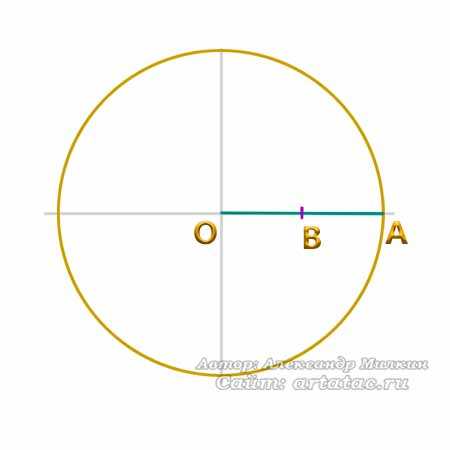
Теперь от точки В до точки С проведем прямую.

 

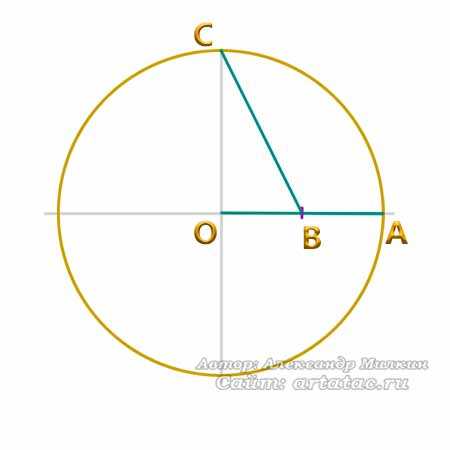
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

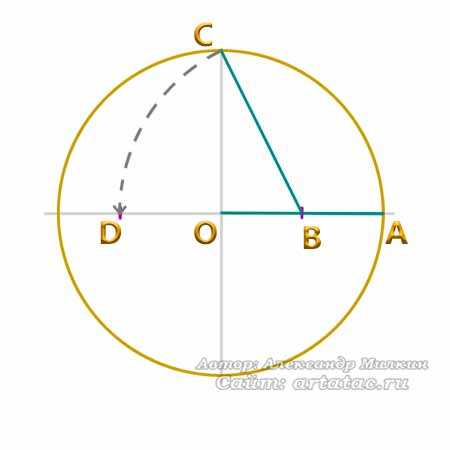
И отрезок DB. Картинка внизу.

 

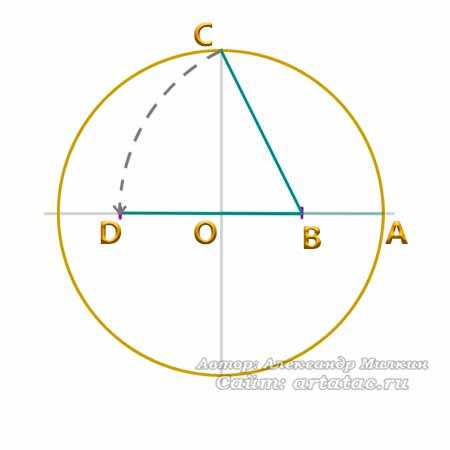
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

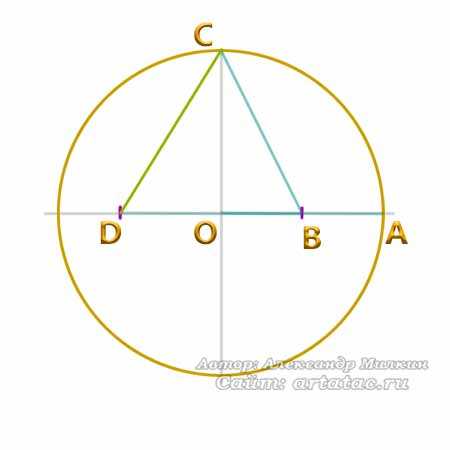
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

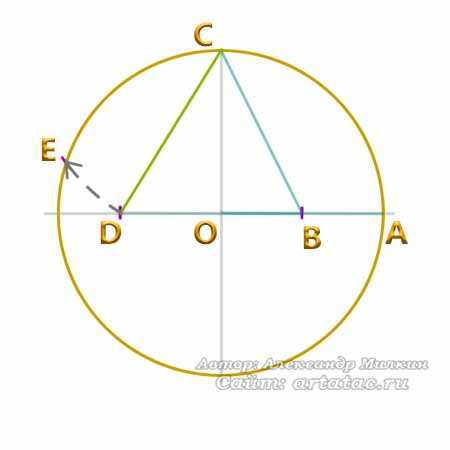
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

 

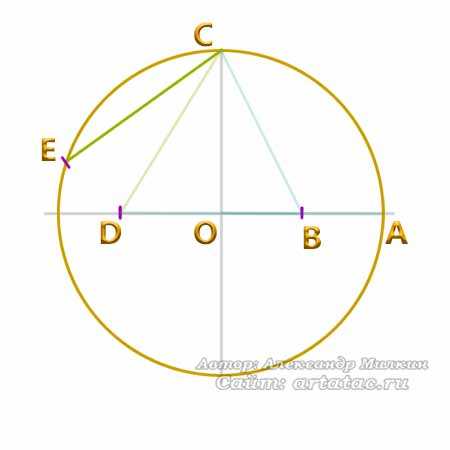
Такие же отрезки наносим на всей части круга. Смотрим картинку.

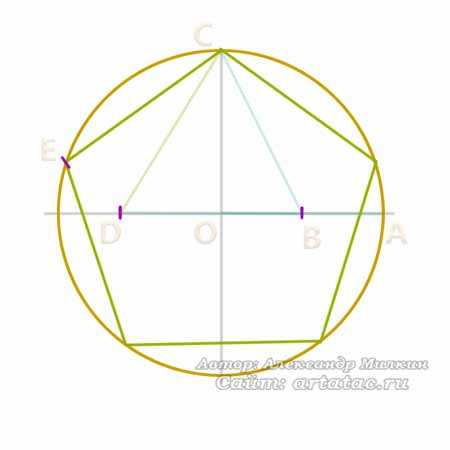
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

 

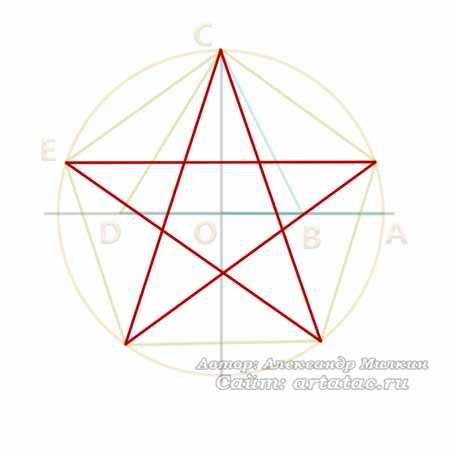
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника,  разделение на восемь частей, деление круга на семь частей, десять равных частей.

 

artatac.ru

КАК ЧЕРТИТЬ ПЯТИУГОЛЬНИК… Способ построения пятиугольника с помощью циркуля и линейки

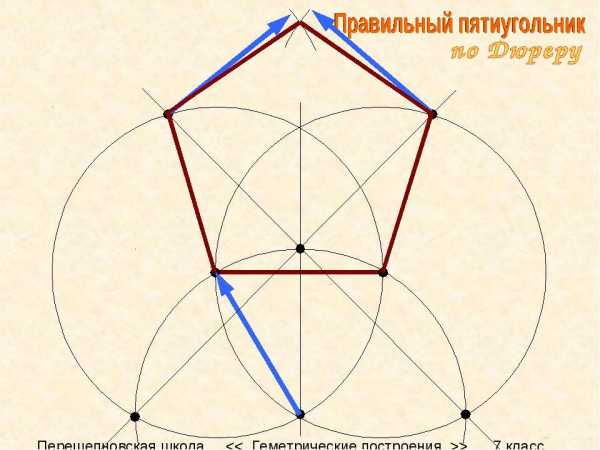Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника. Дальше этот отрезок можно отложить на окружности. Такие же отрезки наносим на всей части круга. Смотрим картинку.

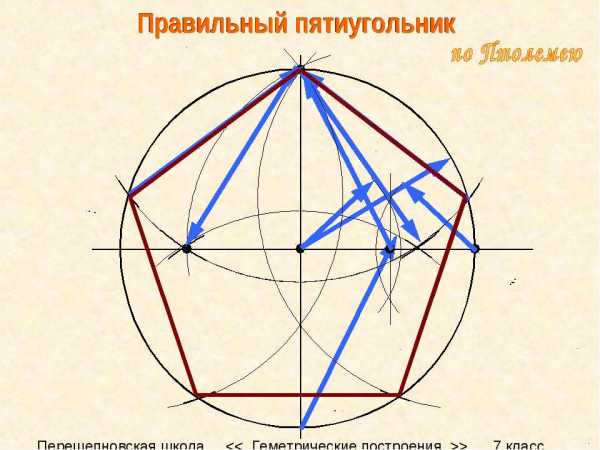
Совет 4: Как начертить луч

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Получение с помощью полоски бумаги

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.

С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».

В тренде:

• Специалисты – кто это?Специалисты – это специализированные работники, которые занимаются разработкой тактики действий. В большинстве случаев сотрудники этой категории взаимодействуют с информацией, благодаря […]
• Распечатать алфавитТрафареты букв — это шаблон формата А4 для распечатки и вырезания из бумаги. Красивый шрифт, большие буквы, печатные и прописные вызовут неподдельный интерес у детей, начните развивать […]
• ЛУЧШИЕ ПРИТЧИ О ЛЮБВИ И ДРУЖБЕ НА САЙТЕ ПО ПРОСМОТРАМ ЧИТАТЕЛЕЙНедаром говорят, дерево живёт корнями, а человек — друзьями. Сегодняшние притчи о дружбе расскажут, кто такие настоящие друзья, как правильно их выбирать и насколько важно уметь дружить […]

estortenok.ru

Как нарисовать звезду циркулем

Если вам необходимо нарисовать правильную пятиконечную звезду, то вы можете воспользоваться простыми инструментами — транспортиром и линейкой. Сложнее изобразить звезду при отсутствии транспортира. Здесь вам на помощь придет обычный циркуль. Вооружайтесь им, возьмите лист бумаги и приступайте к выполнению задания.

Вам понадобится

• Лист бумаги, циркуль, линейка, карандаш

Инструкция

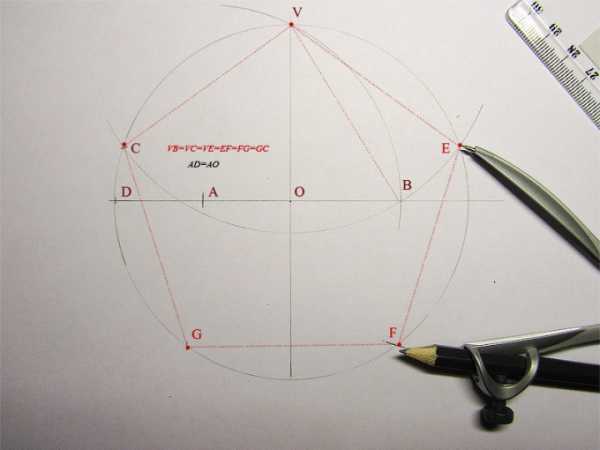
• При помощи циркуля начертите на листе бумаги окружность нужного диаметра с центром в точке O. Построение правильной пятиконечной звезды представляет собой задачу, аналогичную вписыванию в окружность правильного пятиугольника.
• Проведите через окружность диаметр АВ, расположив его горизонтально.
• Восстановите перпендикуляр CD к прямой АВ в точке О. Для этого проведите окружности с центрами в точках А и В с одинаковыми радиусами, а затем проведите прямую линию через точки пересечения этих окружностей.
• Аналогично разделите отрезок АО точкой Е пополам. Для деления отрезка проведите окружности одинакового радиуса с центрами в точках А и О. Теперь соедините точки пересечения окружностей линией — она разделит отрезок АО точно пополам.
• Проведите из точки Е окружность радиусом СЕ и найдите точку F пересечения с отрезком АВ. Отрезок CF является искомым отрезком, равным стороне вписанного пятиугольника.
• Из точки С, расположенной в верхней части окружности, нанесите последовательно по всей окружности отметки так, чтобы они располагались на расстоянии друг от друга, равном CF. Окружность будет разделена на пять равных частей. Точное деление возможно лишь при аккуратном построении при помощи хорошего циркуля.
• Соедините получившиеся на окружности пять точек таким образом, чтобы получилась пятиконечная звезда. Для этого вам понадобится линейка.
• При необходимости вспомогательные линии внутри окружности сотрите ластиком, чтобы они не портили вид звезды. Также можно удалить все остальные штрихи, использованные при построении фигуры.

completerepair.ru

Черчение для лепки

Категория: Лепка

Черчение для лепки

При лепных работах приходится выполнять всевозможные изделия с прямо- или криволинейным очертанием, например розетки круглой, эллиптической и овальной формы, а также квадратные, прямоугольные, многогранные, треугольные. Многогранные изделия бывают с четным и нечетным числом граней, поэтому любую окружность надо уметь точно разделить на нужное количество граней. Размеры граней (длина, ширина) должны быть одинаковыми, в крайнем случае — с допусками не более 2 мм.

Большое распространение в лепных работах имеют арки: коро-бовые, стрельчатые, полуциркульные, овальные и др. В этом случае приходится вычерчивать спиралевидные кривые.

Часто бывает, что рисунок надо увеличить или уменьшить. О том, как все это делается, мы и расскажем ниже. Для работы необходим чертежный инструмент: циркуль, измеритель, угольники, транспортир, линейка и некоторые другие. Самым простым циркулем является так называемая козья ножка. Этим циркулем пользуются при вычерчивании рисунков или чертежей небольших размеров. Для больших рисунков применяют большие циркули, а если обычные, то с удлиненной ножкой.

Деление прямых линий и окружностей

Деление прямой линии на четыре равные части (рис. 1). Прямую линию АБ необходимо разделить на четыре равные части. Для этого применяют способ засечек. Радиусом, несколько большим половины длины данного отрезка, из концов точек А к Б проводят дуги, которые пересекутся в точках 01 и 02. К точкам пересечения приставляют угольник или линейку и проводят прямую, которая в точке В точно разделит прямую АБ на две равные части.

Затем точно так же полученные половины прямой делят на две равные части и находят точки Г и Д. Таким образом делят прямые линии на любое четное число отрезков.

Точно так же делят на четное число и кривые линии.

Деление прямой на нечетное число равных частей (рис. 2). Прямую линию АБ требуется разделить, например, на семь частей. Для этого на бумаге, картоне, фанере, гипсовой плите и т. д. проводят горизонтальную линию и откладывают на ней циркулем семь одинаковых частей, примерно равных будущим семи частям, и в точки ставят цифры 1…7. К этой линии проводят под любым углом линию АБ нужной длины. К точкам Б я 7 ставят угольник, а под него — линейку и проводят между точками первую линию Б7. Затем угольник передвигают влево до точки 6 и проводят вторую линию и так повеем точкам. Этим способом можно делить только прямые линии.

Рис. 1. Деление прямой линии на четыре равные части

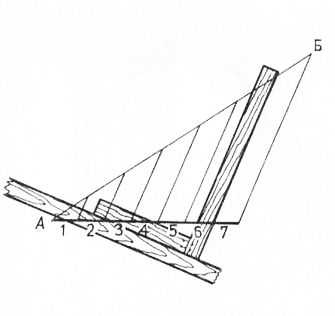
Рис. 2. Деление прямой линии на нечетное число равных частей

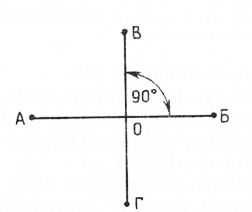
Рис. 3. Построение горизонтальной и вертикальной осей

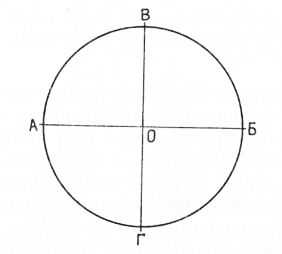
Рис. 4. Деление окружности на четыре равные части

Построение горизонтальной и вертикальной осей.

При вычерчивании многих геометрических фигур необходимо сначала построить (начертить) горизонтальную и вертикальную оси. Для этого проводят горизонтальную линию нужной или произвольной длины и ставят точки АиБ. Делят эту линию на две равные части и ставят точку (центр) О. Через точку О проводят строго вертикальную линию ВГ, которая должна быть под прямым углом, т. е. 90°.

Деление окружности на четыре равные части.

Если через точку О на горизонтальной оси провести строго под прямым углом вертикальную ось, а затем из центра О с помощью циркуля провести окружность, то осями она будет точно разделена на четыре равные части.

Построение разных фигур

Построение треугольника с криволинейными гранями (сторонами), вписанного в окружность. Проводят оси и ставят точку О в месте их пересечения. Из точки О радиусом необходимого размера проводят окружность и делят ее ровно на пять частей по ранее рассмотренному примеру. В местах деления окружности ставят цифры и проводят кривые линии из точки 1 между точками 3 и 5, из точки 3 между точками 1 и 5 и из точки 5 между точками 7 и 3. Таким образом получается треугольник с криволинейными гранями.

Построение окружностей в треугольнике с криволинейными гранями. Если в таком треугольнике необходимо построить три одинаковых окружности, то сначала на осях 1…4, 2…5 и 3…6 следует найти точки (центры) Ov 02 и Оъ, из которых можно было бы выполнить окружности, находящиеся между осями и криволинейными гранями треугольника, т. е., чтобы они вписались в треугольник и только касались друг друга.

Построение десятиконечной звезды. Прежде всего проводят горизонтальную и вертикальную оси, место пересечения осей обозначают точкой О. Затем из этой точки выполняют две окружности радиусом требуемого размера, делят их на десять равных частей, находят точки и соединяют линиями, получая концы звезды.

Построение восьмиконечной звезды. Сначала проводят горизонтальную и вертикальную оси, место их пересечения обозначают точкой О. Затем из центра выполняют две окружности требуемого радиуса, делят каждую из них на восемь равных частей, проводят оси и прямые линии, образуя концы звезды.

Построение розетки с вогнутыми к центру гранями. Проводят горизонтальную и вертикальную оси. Место их пересечения обозначают точкой О. Из центра циркулем выполняют окружность нужного диаметра и делят ее на шесть равных частей. Через каждое деление проводят из центра прямые линии — радиусы 1…6.

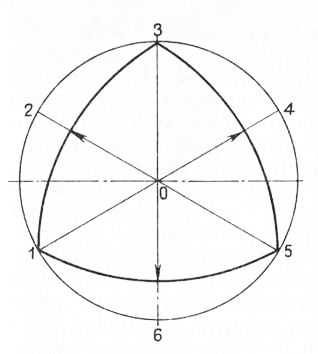
Рис. 5. Построение треугольника с криволинейными гранями, вписанного в окружность

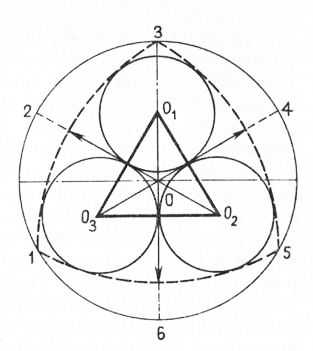
Рис. 6. Построение в окружности, треугольника с криволинейными гранями

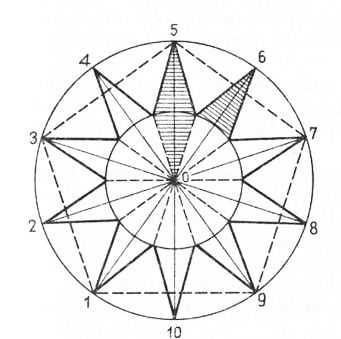
Рис. 7. Построение десятиконечной звезды

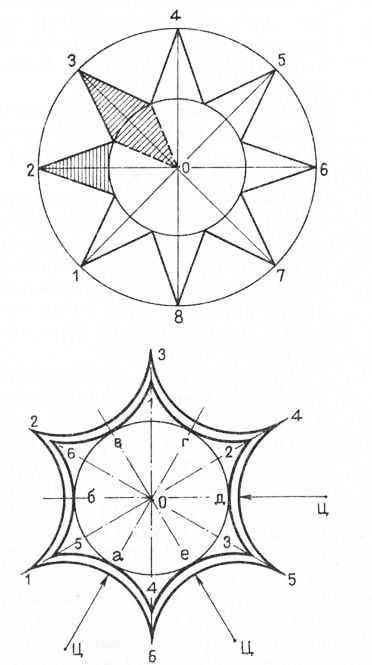
Рис. 8. Построение восьмиконечной звезды

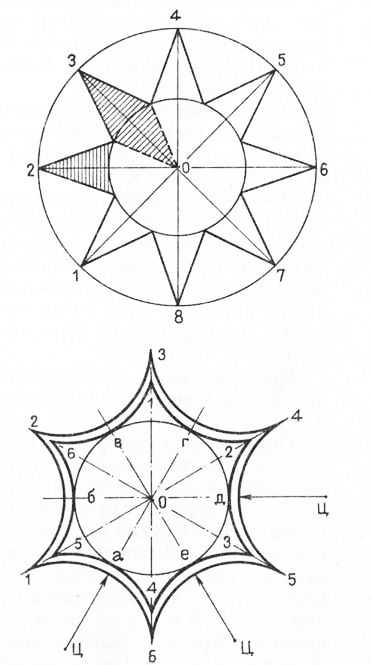
Рис. 9. Построение розетки с вогнутыми к центру гранями

Эти радиусы, или линии ограничения, ограничивают участки для вытягивания граней розетки. Каждую шестую часть окружности делят пополам и на их середине ставят точки а, б, в, г, д, е. Через эти точки из центра проводят линии, которые назовем центровыми осями ц. На центровых осях откладывают от центра отрезки заданной длины, из которых вычерчивают грани (стороны) розетки.

Построение розетки с выпуклыми от центра гранями. Сначала проводят горизонтальную и вертикальную оси. Место пересечения осей обозначают точкой 0. Из этой точки проводят окружность, делят ее на шесть равных частей тем же радиусом, которым была выполнена окружность, и метят точки деления цифрами 1…6. После этого каждую шестую часть окружности делят пополам и на точках деления ставят буквы А…Е. Затем через точки деления проводят прямые и находят центры, с которых будут выполнять выпуклые грани розетки. В середине розетки можно вычертить окружности разного диаметра. Они могут быть просто линиями или подобраны из архитектурных обломов.

Построение розетки с шестнадцатью лепестками. Сначала проводят оси, находят центр, проводят окружность и делят ее на шестнадцать равных частей. Из центра проводят оси, определяющие размеры лепестков. Затем находят центры для больших и малых лепестков.

Построение звезды с прямыми концами. Описывают окружность по размеру звезды и делят ее на пять равных частей. Затем проводят линии из точки 1 в точки 4 и 3, из точки 2 в точку 3, из точки 2 в точку 4.

Построение звезды с закругленными концами. Часто концы звезды имеют не прямую, а закругленную форму. В этом случае сначала строят обыкновенную звезду с прямыми концами. Затем из конечных точек проводят линии ограничения через точки пересечения двух противоположных концов звезды. Из точки 3 линию проводят через точку пересечения концов 1 и 5 звезды, из точки 2 — через точку пересечения концов 4 и 5 (см. пунктирные линии).

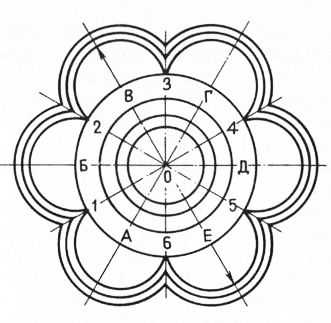
Рис. 10. Построение розетки с вътуклы-ми от центра гранями

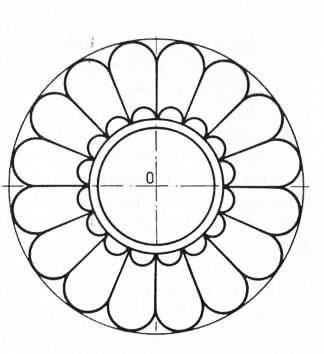
Рис. 11. Построение розетки с шестнадцатью лепестками

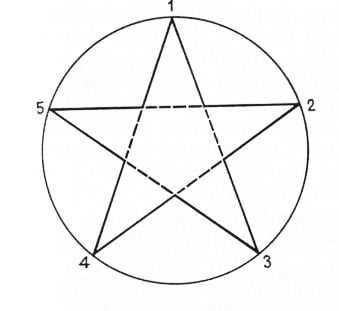
Рис. 12. Построение звезды с прямыми концами

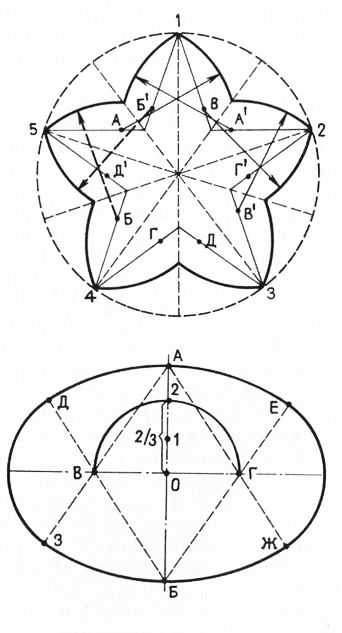
Рис. 13. Построение звезды с закругленными концами

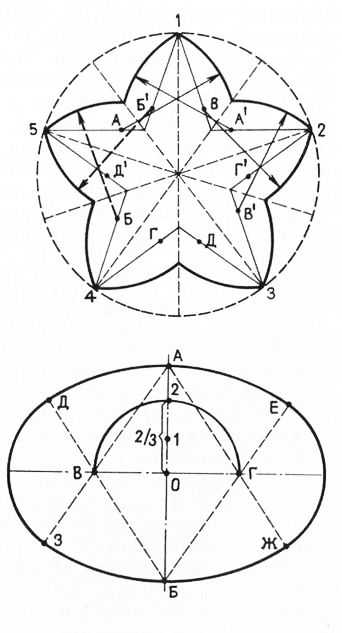
Рис. 14. Построение эллипса по заданной короткой оси

Построение эллипса по заданной длинной оси. В этом эллипсе отношение длинной оси к короткой составляет 1:0,57. Прежде всего проводят горизонтальную и вертикальную оси, и в месте их пересечения находят центр 0 эллипса. Отмеряют от центра две половины оси и ставят на их концах точки А и Б. Каждую половину оси делят на две равные части и находят центры 01 и 02. Радиусом А0Х из центров 0Х и 02 очерчивают окружности, соприкасающиеся в центре 0, и проводят через этот центр короткую ось. Этим же радиусом из центра 0 проводят третью окружность. Выполненные окружности пересекаются в точках В, Г, Д, Е. Из центра 0Х через точки В и Д, а из центра 02 — через точки Г и Е проводят лучи такой длины, чтобы они пересеклись с малой осью (точки Ж и 3) и с окружностью (точки И, М, К, Л). Радиусом, равным отрезку ЖМ, проводят дуги: И К из точки 3 и МЛ из точки Ж до пересечения с ранее проведенными лучами. Затем радиусом 0ХИ из центров 0Х и 02 проводят дуги МИ и KJI, соединяя их с ранее проведенными дугами. Таким образом, для построения указанного эллипса также требуются четыре точки (центры): 0Х, 02, Ж и 3. Точки Ж и 3 вынесены за длинные дуги, вбитые в них гвозди в дальнейшем не мешают вытягиванию эллипса из материала. Напоминаем еще раз, что построение эллипса должно быть очень точным.

Построение эллипса по заданной длинной оси.

В этом эллипсе отношение длинной оси к короткой составляет 1:0,43.

Прежде всего длинную ось эллипса АБ делят пополам, находят центр 0, через который проводят короткую ось. Затем половину длинной оси делят на две равные части и получают два центра: 0х и 02. Радиусом А0Х проводят из этих центров окружности. Параллельно большой оси проводят прямые линии, которые касаются обеих окружностей и пересекаются с малой осью, образуя точки В и Г. Из этих точек через центры 0Х и 02 проводят лучи так, чтобы они пересекли окружности. Из точки Г радиусом ГЕ проводят дугу ЕЖ до пересечения с лучами, а из точки В таким же радиусом — дугу ДЗ также до пересечения с лучами. Из центра 0Х радиусом 0ХЕ проводят дугу ДЕ, а из центра 02 — дугу ЖЗ.

Таким образом, для построения такого эллипса также требуются четыре точки (центры): 0Х, 02, В и Г.

Построение эллипса с двух точек по длинной оси. Проводят горизонтальную ось длиной, несколько большей длины эллипса, и ставят точки А и Б. На этой оси на некотором расстоянии один от другого крепят два гвоздя (две точки): 1 и 2. На эти гвозди надевают шнур 3 со связанными концами, но чтобы шнур был длиннее, чем расстояние между двумя гвоздями. Если связанный шнур вытянуть в какую-то сторону, то он образует как бы угольник. Если этот «угольник» натянуть карандашом и провести вокруг вбитых гвоздей окружность, получится эллипс.

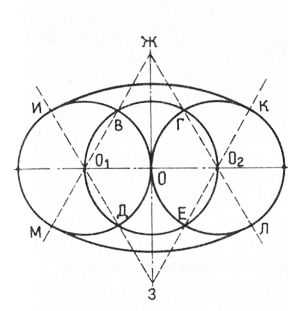
Рис. 15. Построение эллипса по заданной длинной оси

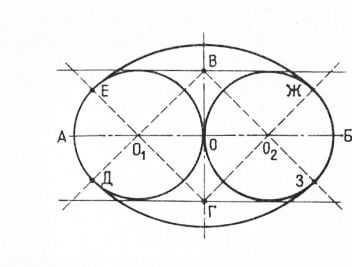
Рис. 16. Построение эллипса по заданной длинной оси с четырех точек

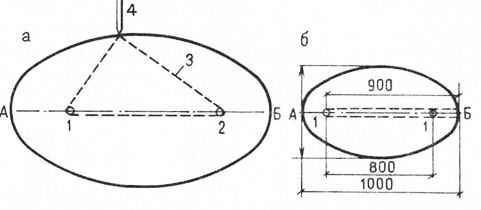
Рис. 17. Построение эллипса с двух точек по длинной оси с помощью шнура а — вытягивание эллипса; б — построение эллипса длиной 1000 мм

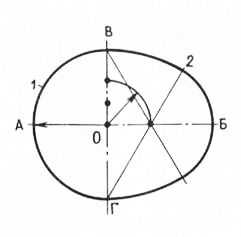
Рис. 18. Построение овала

Форма эллипса зависит от расстояния между гвоздями. Этим же расстоянием определяют необходимую длину шнура. Предположим, что надо вытянуть эллипс с длинной осью 1000 мм. Расстояние между гвоздями должно быть меньше на 100—200 мм, т. е. равняться 800 мм. Длина шнура определяется длиной эллипса плюс расстояние между гвоздями: 1000 + 800 = 1800 мм (без учета узлов). Принято указывать длину шнура, сложенного вдвое, — в данном случае 900 мм.

Зависимость высоты (ширины) эллипса от расстояния между гвоздями при его длине 1000 мм приведена в табл. 1. Чем меньше расстояние между гвоздями, тем ближе форма эллипса к окружности. Зависимость формы эллипса от длины шнура при постоянном расстоянии между гвоздями 1000 мм приведена в табл. 2. Таким образом, чем длиннее шнур при данном расстоянии между гвоздями, тем длиннее эллипс.

Построение овала. Овал состоит как бы из двух частей: одна часть является половиной эллипса, а вторая — половиной круга. Сначала рекомендуется вычертить половину эллипса, а затем разделить ширину эллипса на две части, пересекающие горизонтальную ось, наметить точку 0, из которой выполнить половину круга.

Может возникнуть вопрос, нужно ли рассматривать всю группу эллипсов, не достаточно ли ограничиться построением одного эллипса, так как ширина эллипсов по отношению к длине или наоборот совершенно различные (см. табл.). Еще раз напоминаем, что строить эллипсы надо очень тщательно, чтобы не нарушить их форму. Лепщикам приходится иметь дело не столько с чертежами, сколько с материалом. В этом случае необходимо выполнять так называемое вытягивание, а это большая разница в технике выполнения вытягивания по сравнению с черчением.

В штукатурных работах эллипсы чаще всего вытягивают с помощью креста или патрона Леонардо да Винчи, который дает возможность получать эллипсы разной формы, т. е. при одинаковой длине они могут быть разной ширины.

Построение арок

Полуциркульные арки вычерчивают из одного центра. Сначала проводят горизонтальную и вертикальную оси, определяют центр 0. Из центра радиусом необходимого размера описывают половину окружности, т. е. до уровня центра, с которого вытягивали, а затем идут вертикальные стороны арки.

Пологие арки вычерчивают из одного центра, который находится гораздо ниже самой верхней части арки. Все зависит от того, насколько должна быть поднята криволинейная часть.

Коробовые (лучковые) арки вычерчивают из трех центров, которые подбираются опытным путем или дают в проекте.

Первый центр 0 находится гораздо ниже верхней части арки.

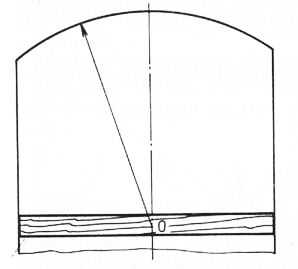
Рис. 19. Построение полуциркульной арки

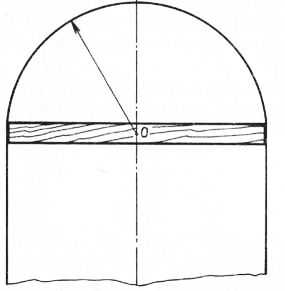
Рис. 20. Построение пологой арки

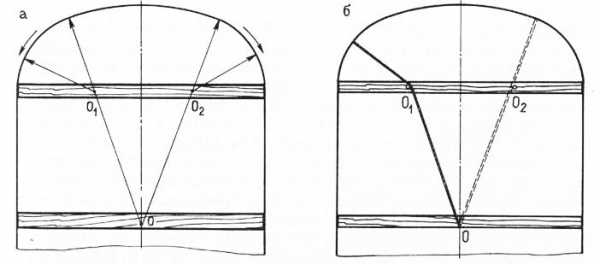
Рис. 21. Построение коробовой лучковой арки а — с помощью шаблона; б — с помощью шаблона на веревке

Рис. 22. Построение стрельчатой простой арки с разным расположением точек а — узкой; б — широкой

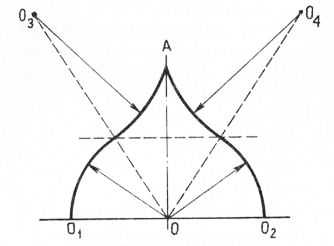
Рис. 23. Построение стрельчатой сложной арки

Рис. 24. Построение арок разной формы

Остальные два центра 0Х и 02 находятся ближе к самой верхней части арки. Чтобы вычертить эту часть арки, проводят три вертикальных оси: одну центральную и две боковых, определяющих ширину арки. Затем к верхней стороне арки проводят две или три горизонтальных оси и по ним подбирают кривую согласно проекту. Сначала вычерчивают самую пологую верхнюю часть, а затем к ней подбирают боковые, закругленные части арки. Для работы необходим циркуль, но можно обойтись и ниткой, рыболовной леской или шпагатом (рис. 56, б). Если в верхнюю горизонтальную ось вбить два гвоздя на одинаковом расстоянии от вертикальных боковых осей или линий арки, а внизу на необходимом расстоянии от верха арки — один гвоздь с закрепленной на нем ниткой, натянуть ее и вращать влево и вправо, то нитка, перегнувшись через точки 0Х и 02, вычертит требуемую кривую.

Стрельчатые простые арки вычерчивают из двух центров. Сначала проводят горизонтальную ось, а перпендикулярно ей — вертикальную, образуя при этом точку 0. От этой точки (центра) отмеряют половину ширины арки и ставят точки 01 и 02. Эти точки в зависимости от ширины арок и кривизны стрелы могут быть около стен арки или с отступом от них. Во избежание вычерчивания стрел различной кривизны точки должны быть определены очень точно.

Стрельчатые сложные арки вычерчивают из четырех или более центров, что зависит от формы арки, т. е. кривизны ее очертаний. Сначала проводят одну горизонтальную ось, а перпендикулярно ей — вертикальную, образуя при этом точку 0. Затем от вертикальной оси отмеряют по половине ширины арки и ставят точки 01 и 02. Из точки 0 вычерчивают часть арки до определенной ее высоты и ставят точки или проводят горизонтальную ось (пунктиром), ограничивая вычерченные арки до нужной высоты. Затем с наружной стороны арки подбирают точки 0Ъ и 04 так, чтобы они дали возможность вытянуть кривые, которые бы сошлись с ранее вытянутыми нижними частями арки и в ее верху, или в так называемом замке.

Разной формы арки встречаются в новом строительстве и в реставрационных работах. Их формы и размеры самые различные. Бывают арки гладкие или состоящие из архитектурных обломов.

Лепка — Черчение для лепки

gardenweb.ru

Построение правильных многоугольников — Техническое черчение

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

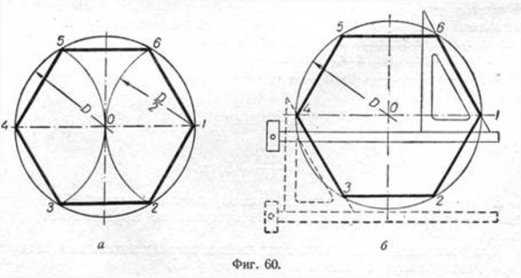
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

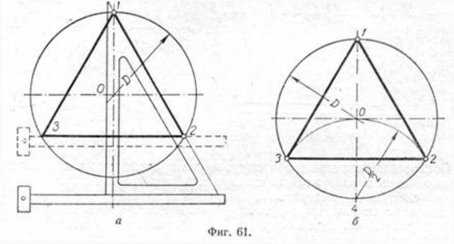
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

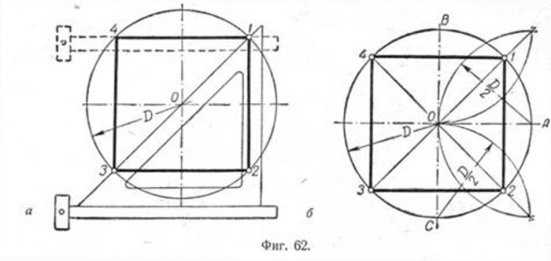
Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

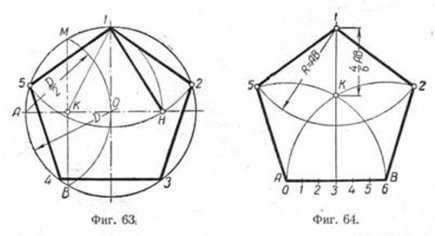
Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

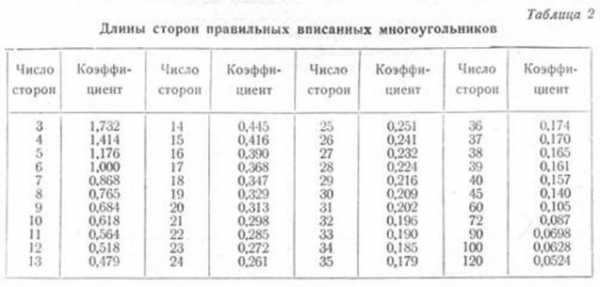
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

www.nacherchy.ru

Реферат Построение с помощью циркуля и линейки

Опубликовать

скачать Реферат на тему: План: Введение 1 Пример 2 Формальное определение 3 Известные задачи 3.1 Построение правильных многоугольников 3.2 Неразрешимые задачи 4 Возможные и невозможные построения 5 Вариации и обобщения 6 Интересные факты 7 См.также Примечания Литература Введение Построения с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности: Линейка не имеет делений и имеет только одну сторону бесконечной длины. Циркуль может иметь сколь угодно большой или сколь угодно малый раствор. 1. Пример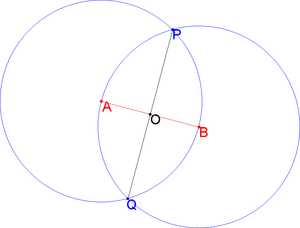 Разбиение отрезка пополам Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке: Циркулем проводим окружности с центром в точках A и B радиусом AB. Находим точки пересечения P и Q двух построенных окружностей (дуг). По линейке проводим отрезок или линию, проходящую через точки P и Q. Находим искомую середину отрезка AB — точку пересечения AB и PQ. 2. Формальное определение В задачах на построение рассматриваются множество всех точек плоскости, множество всех прямых плоскости и множество всех окружностей плоскости, над которыми допускаются следующие операции: Выделить точку из множества всех точек: произвольную точку произвольную точку на заданной прямой произвольную точку на заданной окружности точку пересечения двух заданных прямых точки пересечения/касания заданной прямой и заданной окружности точки пересечения/касания двух заданных окружностей «С помощью линейки» выделить прямую из множества всех прямых: произвольную прямую произвольную прямую, проходящую через заданную точку прямую, проходящую через две заданных точки «С помощью циркуля» выделить окружность из множества всех окружностей: произвольную окружность произвольную окружность с центром в заданной точке произвольную окружность с радиусом, равным расстоянию между двумя заданными точками окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками В условиях задачи задается некоторое множество точек. Требуется с помощью конечного количества операций из числа перечисленных выше допустимых операций построить другое множество точек, находящееся в заданном соотношении с исходным множеством. Решение задачи на построение содержит в себе три существенные части: Описание способа построения заданного множества. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом. 3. Известные задачи Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений. Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам. 3.1. Построение правильных многоугольников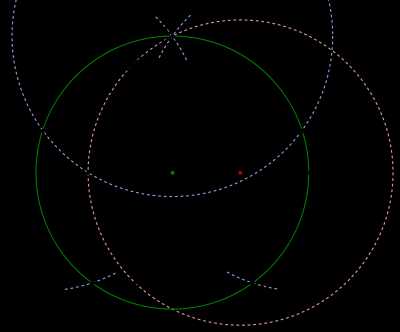 Построение правильного пятиугольника Античным геометрам были известны способы построения правильных n-угольников для , , и . В 1796 году Гаусс показал возможность построения правильных n-угольников при , где — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. 3.2. Неразрешимые задачи Следующие три задачи на построение были поставлены ещё в античности: Трисекция угла — разбить произвольный угол на три равные части. Удвоение куба — построить ребро куба вдвое большего по объёму, чем данный куб Квадратура круга — построить квадрат, равный по площади данному кругу. Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа. Другая известная неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным биссектрисам.[1] Причём эта задача остаётся неразрешимой даже при наличии трисектора.[2] 4. Возможные и невозможные построения Все построения являются ничем иным, как решениями какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований возможны следующие построения: Построение решений линейных уравнений. Построение решений квадратных уравнений. Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например, Если задан только отрезок длины 1, то невозможно представить в таком виде (отсюда невозможность удвоения куба). Возможность построить правильный 17-угольник следует из выражения на косинус угла: 5. Вариации и обобщения Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки. Построения с помощью одной линейки. Легко заметить, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности, невозможно даже разбить отрезок на две равные части, либо найти центр нарисованной окружности. Но при наличии на плоскости заранее проведённой окружности с отмеченным центром с помощью линейки можно провести те же построения, что и циркулем и линейкой (теорема Понселе — Штейнера (англ.)), 1833. Если на линейке есть две засечки, то построения с помощью неё эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон). Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу. Построения с помощью плоского оригами. см. правила Худзита 6. Интересные факты Узор на флаге Ирана описывается как построение с помощью циркуля и линейки[3]. 7. См.также Программы динамической геометрии позволяют выполнять построения с помощью циркуля и линейки на компьютере. Примечания Кто и когда доказал невозможность построения треугольника по трем биссектрисам? — www.mccme.ru/ask/qa/bissect.html. Дистанционный консультационный пункт по математике МЦНМО. Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор — www.mccme.ru/ask/qa/bissect1.html. Дистанционный консультационный пункт по математике МЦНМО. Стандарт флага Ирана — www.isiri.org/std/1.htm (перс.) Литература А. Адлер Теория геометрических построений — ilib.mccme.ru/djvu/geometry/adler.htm / Перевод с немецкого Г. М. Фихтенгольца. — Издание третье. — Л.: Учпедгиз, 1940. — 232 с. И. И. Александров Сборник геометрических задач на построение — ilib.mccme.ru/djvu/geometry/alexandrov.htm. — Издание восемнадцатое. — М.: Учпедгиз, 1950. — 176 с. Б. И. Аргунов, М. Б. Балк Геометрические построения на плоскости. Пособие для студентов педагогических институтов — ilib.mccme.ru/djvu/geometry/geopost.htm. — Издание второе. — М.: Учпедгиз, 1957. — 268 с. А. М. Воронец Геометрия циркуля — ilib.mccme.ru/djvu/geometry/voronec.htm. — М.-Л.: ОНТИ, 1934. — 40 с. — (Популярная библиотека по математике под общей редакцией Л. А. Люстерника). В. А. Гейлер Неразрешимые задачи на построение — www.pereplet.ru/nauka/Soros/pdf/9912_115.pdf // СОЖ. — 1999. — № 12. — С. 115—118. В. А. Кириченко Построения циркулем и линейкой и теория Галуа — www.mccme.ru/dubna/2005/notes/kirichenko.ps.gz // Летняя школа «Современная математика». — Дубна: 2005. Ю. И. Манин Книга IV. Геометрия // Энциклопедия элементарной математики — ilib.mccme.ru/djvu/encikl/enc-el-4.htm. — М.: Физматгиз, 1963. — 568 с. Ю. Петерсен Методы и теории решения геометрических задач на построение — ilib.mccme.ru/djvu/geometry/krutikov.htm. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — 114 с. В. В. Прасолов Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга — www.math.ru/lib/book/plm/v62.djvu. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике). Я. Штейнер Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга — ilib.mccme.ru/djvu/geometry/shteiner.htm. — М.: Учпедгиз, 1939. — 80 с. Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3 скачать Данный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 09.07.11 10:03:45 Похожие рефераты: Список звёзд созвездия Циркуля, Каре (построение), Колонна (построение), Сторожевая башня (построение), Как питаться с помощью задницы, С помощью зеркал (роман). Категории: Геометрические построения. Текст доступен по лицензии Creative Commons Attribution-ShareAlike.

wreferat.baza-referat.ru