Фото цилиндр фигура – Ой!

Цилиндр, конус, шар, развёртка цилиндра и конуса

Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.

Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).

Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.

Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.

В курсе математики для б класса рассматриваются только прямые цилиндры и конусы

.

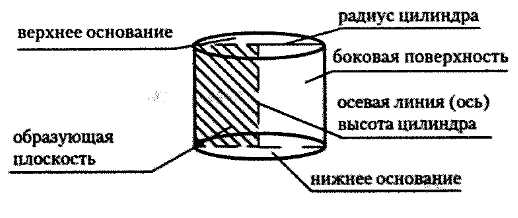
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.

Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.

Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.

Развертки цилиндра и конуса

Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.

Развертка цилиндра приведена схематически.

Развертка конуса приведена схематически.

Площади боковой поверхности цилиндра и конуса

Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.

где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.

Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Площадь поверхности шара

Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.

где R — радиус шара.

Объемы цилиндра, конуса и шара

Правило. Объем цилиндра равен произведению площади основания н высоты.

где R — радиус основания, H — высота цилиндра.

Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.

где R — радиус основания, H — высота конуса.

Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.

где R — радиус шара.

shkolo.ru

§9. Изображение цилиндра

1. Пусть цилиндр-оригинал F; ¯ расположен так, что его ось O; ¯O1;¯ параллельна плоскости изображений . Направление прое­цирования выберем следующим образом. Через ось цилиндра проведём плоскость  и выберем направление проецирования параллельно этой плоскости, но не параллельно основаниям цилиндра (иначе изображение будет выглядеть, как прямоугольник, и не будет наглядным).

Пусть (;¯ – окружность верхнего основания цилиндра, A; ¯B; ¯ и C; ¯D; ¯ – взаимно перпендикулярные диаметры этой окружности, причём A; ¯B; ¯||, C; ¯D; ¯. Тогда C; ¯D; ¯. Проведём образующие A; ¯A1;¯, B; ¯B1;¯, которые будем называть контурными. Пусть l1;¯ и l2;¯ – касательные к окружности (;¯ в точках A; ¯ и B; ¯. При проецировании окружность (;¯ переходит в эллипс  с осями

AB и CD. Отрезок A; ¯A1;¯ и прямая l1;¯ лежат в плоскости, параллельной направлению проецирования, поэтому они проецируются на одну прямую l₁. При этом, прямая l1;¯ была касательной к (;¯. Следовательно, изображение AA₁ контурной образующей лежит на каса­тельной к эллипсу . Аналогично ВВ₁ тоже лежит на касательной к эллипсу .

Дополнительно потребуем, чтобы угол между вектором p;\s\up8(( и осью цилиндра был больше 45. Тогда на изображении будет |AB|>|CD|. Итак, мы окончательно имеем следующее изображение.

10 Изоброжение конуса

2. Выберем плоскость изображения  параллельно оси S; ¯O; ¯ данного конуса (; ¯. Пусть  – плоскость основания конуса, а  – плоскость, проходящая через ось цилиндра, перпендикулярно . Направление прое­цирования выберем следующим образом. Через вершину S; ¯ проведём прямую l;¯ в плоскости , так чтобы она пересекала плоскость  в точке K; ¯, расположенной вне основания конуса, и так чтобы угол между высотой S; ¯O; ¯ и прямой l;¯ был больше 45. Теперь выберем направление проецирования параллельно l;¯.

Пусть (;¯ – окружность основания конуса, A; ¯B; ¯ и C; ¯D; ¯ – взаимно перпенд-ые диаметры этой окружности, причём A; ¯B; ¯||, C; ¯D; ¯. Тогда C; ¯D; ¯. Проведём касательные K; ¯M; ¯, K; ¯N; ¯ к (;¯. Образующие S; ¯M; ¯ и S; ¯N; ¯ назовём контурными.

При проецировании окружность (;¯ переходит в эллипс с осями AB и CD. Прямые S; ¯O; ¯ и C; ¯D; ¯ лежат в плоскости  параллельной направлению проецирования, поэтому S; ¯O; ¯ и C; ¯D; ¯ проецируются на одну прямую. Точки S; ¯ и K; ¯ проецируются в одну точку, поэтому проекции отрезков K; ¯M; ¯ и S; ¯M; ¯ совпадают. Значит, изображение

SM контурной образующей будет касательной к . Аналогично, SN – тоже касательная. Хорда M; ¯N; ¯ параллельна A; ¯B; ¯. Поэтому и на изображении MN||AB.

Самое главное, что следует уяснить: изображения контурных образующих ни в коем случае не проходят через концы главного диаметра эллипса.

§11. Изображение шара.

Пусть (; ¯ – шар-оригинал. Проведём все возможные касательные к шару параллельные направлению проецирования. Они образуют цилиндрическую поверхность, которая касается шара по большой окружности (;¯. В пересечении цилиндрической поверхности с плоскостью изображений

получится эллипс _o, который наз.очертанием шара. Этот эллипс вместе со своей внутренностью будет проекцией шара (обозначаем _o).

Если направление проецирования p;\s\up8(( не перпендикулярно плоскости изображений, то _o не является окружностью. Не будет окружностью и любая подобная 

o фигура. Такое изображение не будет наглядным. Поэтому мы рассмотрим только изображение шара в ортогональной проекции.

Для того, чтобы сделать изображение более наглядным, кроме очертания шара рисуют ещё изображение какой-либо большой окружности (;¯ – экватора. Плоскость экватора не должна быть перпендикулярна плоскости . В противном случае, экватор будет изображаться отрезком, и изображение не будет наглядным. Также принято изобр-ть полюса – концы диаметра шара N; ¯S; ¯, перпендик-ого плоскости экватора.

Изучим, как правильно изображать экватор и полюса. Пусть A; ¯B; ¯ и D; ¯ – взаимно перпендикулярные диаметры экватора, причём A; ¯B; ¯||. Пусть A_oB_o и C_oD_o – проекции этих диаметров. Тогда |A_oB_o|=|A; ¯B; ¯|. Обозначим R; ¯ – радиус шара,  – угол между C; ¯D; ¯ и плос­костью . Тогда

|O_oA_o|=R; ¯,

|O_oC_o|=R; ¯·cos, |O_oN_o|=R; ¯·sin.

Изображение шара подобно его проекции. Поэтому на изображении тоже выполняются соотношения

|OC|=|OA|·cos, |ON|=|OA|·sin. (_*)

Проведём через точку C половину хорды CK, а через точку N – половину хорды NM. В OCK и ONM

|OK|=|OM|=|OA|,

|OC|=|OK|·cosKOC=|OA|·cosKOC.

|ON|=|OM|·sinOMN =|OA|·sinOMN.

След, KOC=OMN= и треугол.KOC,

OMN равны. Поэтому|KC|=|ON|,|OC|=|NM|. (3)

Итак.

1. Если дано изображение экватора , мы можем однозначно определить, где располагаются точки

N и S, изображающие полюсы. Пусть AB – большой диаметр для , CD – малый диаметр. Проведём через точку C половину хорды CK параллельно AB. На перпендикуляре к AB, проходящем через точку O отложим отрезки ON и OS, равные CK.

2. Если дано изображение полюсов N и S, мы можем построить изображение экватора. Большой диаметр изображения экватора – это диаметр очертания шара, перпендикулярный NS. Малый диаметр CD лежит на прямой NS. Проведём через точку N – половину хорды NM. Тогда |OC|=|OD|=|NM|.

Ещё раз подчеркнём, чтополюсы лежат на очертании шара тогда и только тогда, когда экватор изображается отрезком.

При построении изображения шара вместе с декартовой СК следует учесть, что оси

Ox и Oy должны проходить через сопряжённые диаметры экватора, а ось Oz – через полюс. Если у нас уже изображена ось Ox, мы проводим вспомогательную хорду изображения экватора, параллельную Ox, и через середину хорды должна проходить Oy.

studfiles.net

Цилиндры — геометрия и искусство

Дом-мастерская архитектора К.С. Мельникова
1927—1929 гг.

Уникальным в доме Мельникова является уже то, что в конце 1920-х годов, когда в СССР шло сворачивание НЭПа, а по всей стране началось строительство домов-коммун, одному человеку разрешили построить частный дом в центре столицы. Конструкции стен и перекрытий дома-мастерской не только оригинальны, но и выполнены на уровне технических изобретений, несколько из которых были Мельниковым впоследствии запатентованы.

Объёмная композиция дома представляет собой два разновысоких вертикальных цилиндра одинакового диаметра, врезанных друг в друга на треть радиуса, образуя тем самым необычную форму плана в виде цифры «8», ориентированную по направлению «север — юг». Более низкий цилиндр со срезанной по вертикали южной частью завершён плоской крышей с открытой террасой. Возвышающийся над ним задний цилиндр имеет покатую кровлю, понижающуюся от центра здания к его северной части.

К. С. Мельников подробно обосновывает преимущества цилиндрической конструкции: «Экономия материалов: Прямая связь архитектурного изучения геометрии с экономическим эффектом. Задача состоит в том, чтобы… площадь пола была окружена минимальным периметром стен. Требуемая площадь, скажем, 1600 кв. м. Высота — величина постоянная… Возьмем параллелепипед, куб и цилиндр… Итак, по трем вариантам периметр составит соответственно 200, 160 и 140 м. Совершенно реальная экономия от формы объема».

Обращённый к Кривоарбатскому переулку главный фасад дома-мастерской имеет строго фронтальную симметричную композицию. В центре срезанной части малого цилиндра находится единственный вход в дом, по сторонам которого расположены два крупных прямоугольных окна. Основную плоскость фасада здания занимает огромное окно-экран, протянувшееся на всю высоту второго этажа.

Более свободно решены фасады заднего, северного цилиндра. Его стены прорезаны 57 шестигранными вертикальными окнами, образующими единый орнамент со своеобразным ритмом повторяющихся элементов, расположенных пятью ярусами. Нижний ряд окон отделён более высоким отрезком глухой стены от четырёх верхних. Второй ярус соответствует второму этажу, три верхних яруса — третьему. Динамику в общую композицию северного фасада вносит необычный рисунок оконных переплётов трёх типов: один у окон первого яруса, другой во втором и четвёртом ярусах и третий — в третьем и пятом ярусах окон.

(википедия)

geometry-and-art.ru

Цилиндр. Формулы и свойства

Определение.

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра).

Цилиндрическая поверхность — поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.

Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Круговой цилиндр

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Прямой круговой цилиндр можно описать, как объёмного фигуру, образующуюся вращением прямоугольника вокруг своей стороны на 360°.

Определение. Радиус цилиндра r — это радиус основания цилиндра.

Определение. Диаметр цилиндра d — это диаметр основания цилиндра.

Определение. Высота цилиндра h — это расстояние между основаниями цилиндра.

Определение. Ось цилиндра — это прямая O₁O₂, которая проходит через центры оснований цилиндра.

Определение. Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.

Определение. Осевое сечение цилиндра — это сечение цилиндра плоскостью, проходящей через ось цилиндра.

Определение. Касательная плоскость к цилиндру — это плоскость, которая проходит через образующую цилиндра и перпендикулярно к осевому сечении цилиндра.

Формула. Объём цилиндра:

V = πr2h = π	d2	h ,
	4

где r — радиус основы, h — высота цилиндра, d — диаметр основы. Формула. Площадь ,боковой поверхности цилиндра:

S_b = 2πrh = πdh

Формула. Полная площадь поверхности цилиндра:

S = 2πr(h + r)

Косой цилиндр — цилиндр, основы которого не параллельны (Рис.2)

Наклонный цилиндр — цилиндр, у которого образующие не перпендикулярно основам цилиндра (Рис.3 — наклонный круговой цилиндр).

ru.onlinemschool.com

Цилиндр с картинками | mamadelkimamadelki

Маленьким детям очень полезно рассматривать картинки, но бумажные картинки они мнут, рвут и обслюнявливают. Выход – сделать картинки на цилиндрах. Когда малыш вращает цилиндр, перед ним появляются разные картинки. Так ребенок знакомится с животным миром. У меня два таких цилиндра – один с животными наших лесов, а второй с животными других континентов. Нужно выбирать картинки, которые знакомы Вашему ребенку. Это могут быть и фрукты, овощи, игрушки и даже фотографии близких.

Как я это сделала.

Взяла цилиндрическую коробку от чипсов (можно так же коробку из под чая для кормящих мам HIPP или Тип-Топ). Приклеила три полосы двухстороннего скотча по диаметру. Обернула блестящей переливающейся пленкой для подарков. (Удобно так же взять самоклеющуюся блестящую бумагу). Картинки наклеила поперек цилиндра с помощью все того же двухстороннего скотча. Сверху весь цилиндр обклеила прозрачным широким скотчем. Во внутрь положила горох, чтобы игрушка еще и гремела как погремушка. Крышку тоже проклеила скотчем, чтобы ребенок, побуждаемый огромным любопытством, не открыл.

Для тех, кто загорелся сделать своему малышу такую же игрушку, но боится, что будет долго искать подходящие картинки – я предлагаю рисунки, которые использовала сама. Распечатайте на фотобумаге во весь лист.

Играем с ребенком – крутим банку и показываем разные картинки. Называем их и рассказываем о них. Попросите малыша найти какую-нибудь картинку. Например: «Где собачка?», «Где обезьянка?» и т.п.

Вот такая простая в изготовлении развивающая игрушка.

 

Вам будет интересно:

Запись опубликована в рубрике Из ненужных вещей. Добавьте в закладки постоянную ссылку.

mamadelki.ru

Развёртки геометрических фигур

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура – ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

modelmen.ru