Пошаговое построение сечения: треугольная пирамида.
В этой статье мы построим несколько сечений треугольной пирамиды, будем при этом использовать метод следов. Сначала мы рассмотрим самые простые случаи: когда точки, через которые должно пройти сечение, принадлежат ребрам пирамиды. Потом – случаи сложнее, когда одна или две из точек плоскости сечения принадлежат граням пирамиды. Поехали!
Задача 1. Построить сечение пирамиды, проходящее через точки P, Q, R.
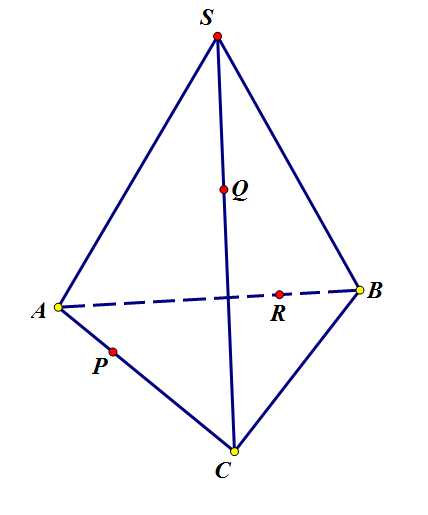
Дано
Сначала надо попробовать отыскать такие точки, которые принадлежат одной плоскости. У нас это точки P и Q – они принадлежат грани ASC, а также пара P и R – они принадлежат грани ABC. Их можно сразу соединять:
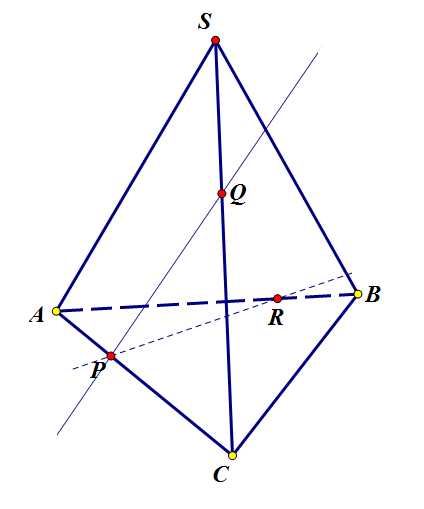
Шаг 1
Теперь, чтобы понять, как плоскость рассечет грань SBC, нужно заполучить точку в этой грани, или в плоскости, которой принадлежит грань. Но нужна нам не любая, а особенная точка, которая также будет принадлежать и плоскости сечения. Чтобы точка принадлежала плоскости нужно, чтобы она принадлежала прямой этой плоскости. Заметим, что прямая PR лежит в плоскости основания и принадлежит искомому сечению. Прямая CB тоже лежит в плоскости основания, но не только. Она еще лежит в плоскости грани SBC, где нам необходима точка, чтобы построить сечение. Воспользуемся случаем: найдем точку, где прямые PR и CB пересекутся. Такая точка принадлежит сечению, а также плоскостям боковой (SBC) и нижней (ABC) граней пирамиды.
Шаг 2
Так как построенная точка T и точка Q лежат в одной плоскости, то можем соединить их прямой:
Шаг 3
Эта прямая пересечет ребро SB в точке F – это и есть еще одна нужная нам точка для построения сечения. Соединяем R и F – они лежат в одной плоскости (SAB). Теперь смотрим: можно ли пройти по линиям сечения, принадлежащим граням пирамиды, от точки P и снова попасть в нее непрерывным маршрутом? Если да, то построение окончено. У нас такой маршрут замкнутый: P-Q-F-R-P. Это и есть сечение.
Шаг 4
Задача 2. Построить сечение пирамиды, проходящее через точки P, Q, R.
Дано
Видим, что точки P и Q принадлежат одной грани пирамиды – SCB – и соединяем их.
Шаг 1
Можно, конечно, было бы сразу и точки P и Q соединить – они тоже лежат в одной плоскости – плоскости грани SAB. Но это успеется, пока что нам нужна точка в плоскости грани SAC, да такая, чтобы принадлежала и сечению. Поэтому она должна принадлежать прямой искомого сечения, и прямой, принадлежащей плоскости SAB, то есть быть пересечением таких прямых. Продлим SC до пересечения с прямой QR -и получим такую точку.
Шаг 2
Точка X и точка P принадлежат одной плоскости, можем их соединить и получить точку пересечения данной прямой с ребром AC:
Шаг 3
Соединяем E с R, P с Q, и получаем сечение.
Шаг 4
Задача 3. Построить сечение пирамиды, проходящее через точки P, Q, R.
Дано
Теперь, уже имея опыт, первый шаг выполняем без проблем:
Шаг 1
Понимаем, что нет точки в задней грани. Вернее, одна есть – P – но второй не хватает. Аналогично, есть одна точка в нижней грани – в плоскости основания, а второй точки нет. Определим такую точку: пересечем AC и PQ. Обе прямые лежат в плоскости SAC, PQ принадлежит плоскости сечения, поэтому их пересечение будет принадлежать обеим плоскостям:
Шаг 2
Теперь имеем две точки в плоскости основания – U и R, и можем смело соединять их:
Шаг 3
Прямая UR пересечет ребро AB в точке Z. Теперь маршрут Q-R-Z-P-Q замкнут, можем достраивать сечение:
Шаг 4
Задача 4. Построить сечение пирамиды, проходящее через точки P, Q, R, причем точка P принадлежит грани ASC.
Дано
Тут уже задача сложнее. Но пока метод следов позволяет ее решить.
Имеем две точки в одной плоскости – Q и R, и можем их сразу же соединять. AS так же, как и QR, принадлежит плоскости задней грани, поэтому продолжение AS пересечет QR в точке L, также принадлежащей плоскости задней грани.
Шаг 1
Но, так как AS принадлежит также и плоскости боковой грани SAC, то точка L лежит с точкой P в одной плоскости и их можно соединять:
Шаг 2
LP пересечет ребро AC в точке M, а ребро SC – в точке N, и можно восстанавливать четырехугольник сечения:
Шаг 3
easy-physic.ruКак начертить пирамиду 🚩 как рисовать треугольную пирамиду 🚩 Математика
Автор КакПросто!
Представления о пространстве у учащихся 5-х классов уже сформированы достаточно хорошо, чтобы они понимали, как начертить объемные геометрические фигуры. Чтобы у вашего ребенка не возникло трудностей при построении фигур в школе, научите его чертить пирамиду.
Статьи по теме:
Инструкция
Чтобы начертить треугольную пирамиду сначала поставьте точку, обозначив центр нижней части пирамиды. От этой точки проведите при помощи карандаша и линейки косую линию немного вверх и вправо. Проведите симметричную линию той же длины на туже высоту влево. От точки центра проведите прямую линию вертикально вверх на высоту, вдвое больше одной из линий. Соедините боковые линии от нижних линий к верхней. Проведите горизонтальную линию, чтобы в нижней части пирамиды у вас получился маленький треугольник с вершиной, направленной вниз. Заштрихуйте полученный треугольник горизонтальными линиями, чтобы показать, что он находится внутри пирамиды. Боковые стороны пирамиды заштрихуйте вертикальными линиями. Треугольная пирамида готова.Чтобы начертить четырехугольную пирамиду проведите горизонтальную линию. Над ней на некотором расстоянии проведите еще одну линию той же длины, только немного правее. Соедините боковые линии, чтобы у вас получился скошенный вправо прямоугольник. В полученном прямоугольнике поставьте точку в его центре. Проведите вертикальную линию вверх. Эта линия должна по длине превышать вдвое длину боковой стороны прямоугольника. Из четырех углов прямоугольника проведите вверх линии к верхней точке центральной линии. Четырехугольная пирамида готова.
Чтобы начертить пятиугольную пирамиду примените тот же метод. Сначала начертите пятиугольную фигуру. Поставьте точку, обозначающую ее центр. Из этой точки проведите вертикальную линию вверх. Проведите линии вверх от углов пятиугольника к верхней точке центральной линии. Пятиугольная пирамида готова.
Совет полезен?
Распечатать
Как начертить пирамиду
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Правильные пирамиды — объёмные геометрические тела
Готовый набор «Волшебные грани»
Для сборки многогранников мы можем вам предложить уже готовые развёртки — вырезанные и подогнутые.
Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.
Кроме того, в самом выпуске вы найдете информацию о строении многогранников.
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка усечённой четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка пирамиды со звёздчатым основанием:
Вращение готового многогранника, собранного из этих деталей:
Сборка би-пирамиды с основанием в форме пятиконечной звезды:
Вращение готового многогранника, собранного из этих деталей:
mnogogranniki.ru
Усечённые пирамиды — геометрические тела
Готовый набор «Волшебные грани»
Для сборки многогранников мы можем вам предложить уже готовые развёртки — вырезанные и подогнутые.
Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.
Кроме того, в самом выпуске вы найдете информацию о строении многогранников.
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Вращение готового многогранника (усечённой четырехугольной пирамиды), собранного из этих деталей:
Сборка пирамиды со звёздчатым основанием:
Вращение готового многогранника, собранного из этих деталей:
Сборка би-пирамиды с основанием в форме пятиконечной звезды:
Вращение готового многогранника, собранного из этих деталей:
mnogogranniki.ru
Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр
В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока.
Определение
Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
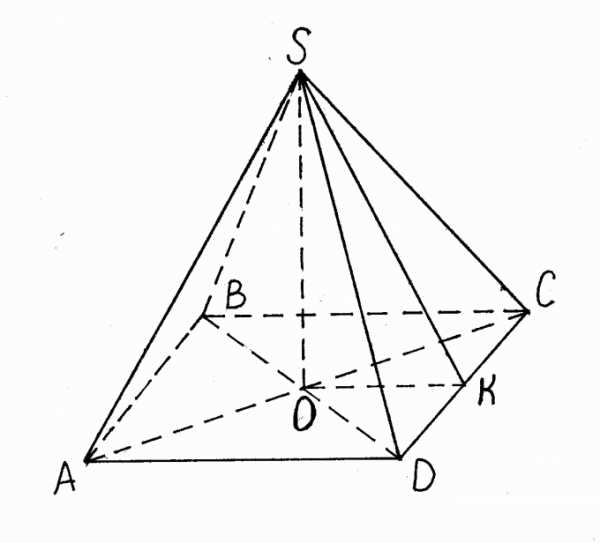
На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)
Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).
Свойства правильной треугольной пирамиды:
- боковые ребра правильной пирамиды равны
- все боковые грани правильной пирамиды являются равнобедренными треугольниками
- в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
- если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
- вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан
Формулы для правильной треугольной пирамиды
Формула объема правильной треугольной пирамиды:
где
V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности
Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.
Примеры решения задач:
Тетраэдр
Частным случаем правильной треугольной пирамиды является тетраэдр.
Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.
У тетраэдра:
- Все грани равны
- 4 грани, 4 вершины и 6 ребер
- Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)
Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)
Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).
Тетраэдр обладает следующими свойствами:
- Все медианы и бимедианы тетраэдра пересекаются в одной точке
- Эта точка делит медианы в отношении 3:1, считая от вершины
- Эта точка делит бимедианы пополам
Площадь, объем, высота, радиус вписанной и описанной окружности и другие формулы для тетраэдра
См. пример задачи: формулы и свойства тетраэдра.
Содержание главы:
Пирамида с равнобедренным треугольником в основании | Описание курса | Периметр основания правильной треугольной пирамиды
profmeter.com.ua
Как сделать правильную пирамиду 🚩 как сделать пирамиду из треугольников 🚩 Образование 🚩 Другое
Автор КакПросто!
Правильная пирамида — это разновидность пирамид, у которой в основании лежит правильный четырехугольник — квадрат. Боковые же грани пирамиды представляют из себя равнобедренные треугольники. Исходя из этих данных, правильную пирамиду довольно легко построить.
Статьи по теме:
Вам понадобится
- Карандаш, лист разлинованной в клеточку бумаги, линейка, ножницы, скотч/изолента для скрепления граней.
Инструкция
Сначала берется лист бумаги, а затем на нем рисуется квадрат примерно таким образом, как это показано на рисунке 2.
Затем нужно начертить 4 равнобедренных треугольника так, чтобы стороны квадрата стали основаниями этих треугольников. Нельзя забывать, что равносторонний треугольник является разновидностью равнобедренного. Это принципиально лишь в том случае, если нужно сделать высокую/невысокую пирамиду. Основание же треугольников останется неизменным. Вариант чертежа представлен на рисунке 3. 
Теперь берутся ножницы и вырезается получившее подобие четырехконечной звезды. Потом «лучи» это «звезды» сгибаются в одну сторону, где будет вершина пирамиды. Если все сделано верно, то из треугольников выйдут грани пирамиды, кончики «лучей» соединятся в одном месте и образуют вершину пирамиды. Затем грани скрепляются и получается то, что изображено на самом первом рисунке.
Источники:
- как правильно сделать пирамиду
- Видео на тему как сделать пирамиду
Совет полезен?
Распечатать
Как сделать правильную пирамиду
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Урок геометрии на тему «Правильная пирамида»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- ввести понятие правильной пирамиды и ее элементов;
- рассмотреть виды пирамид;
- формировать навыки изображения рассматриваемых объектов на плоскости и чтение предлагаемых изображений;
- научиться применять формулы для вычисления площадей поверхностей правильных пирамид при решении задач;
- повышать заинтересованность учащихся к познанию окружающего мира.
Ход урока
I . Повторение
Устная работа
а) Что называется пирамидой, основанием пирамиды, боковыми гранями, боковыми ребрами, вершиной, высотой? Слайд 4.
б) Что называется площадью боковой поверхности пирамиды, площадью полной поверхности пирамиды? Слайд 5.
Работа по группам .
Учитель дает каждой группе задание по карточкам на 2-3 минуты. Через документ-камеру на экран демонстрируется выполненное каждой группой задание. Когда представитель каждой группы показывает свой чертеж, дополнительно задаются вопросы и решаются устные задачи.
- 1-й группе: начертить треугольную пирамиду DАВС, основание высоты которой (т.О) проецируется в центр основания. Отметить угол a между боковым ребром DС и плоскостью основания. (устно: высота пирамиды равна 6 см, а = 30o. Найти боковое ребро DC.)
- 2-й группе: начертить треугольную пирамиду DАВС, основание высоты которой (т.О) проецируется в вершину основания (С). Отметить угол между боковым ребром ВD и плоскостью основания. (устно: найти tg а, если BD = 5 см, высота пирамиды равна 4 см.)
- 3-й группе: начертить треугольную пирамиду DАВС, основание высоты (т.О) которой проецируется в центр основания. Отметить двугранный угол DАВС. (устно: на что вы опирались при построении линейного угла?)
- 4-й группе: начертите прямоугольную пирамиду КАВСD, основание высоты которой проецируется в вершину основания (D). Отметьте угол между ребром ВК и плоскостью основания. (устно: найти высоту пирамиды, если стороны основания равны 4 и 3, а боковое ребро ВК = 13.)
- 5-й группе: начертите четырехугольную пирамиду КАВСD, основание высоты (т.О) которой проецируется в центр основания. Отметить угол a между ребром КВ и плоскостью основания. (устно: высота пирамиды равна 6 см, а = 45o. Найти боковое ребро BK.)
- 6-й группе: начертить треугольную пирамиду DАВС, основание высоты (т.О) которой проецируется в вершину основания (С). Отметить двугранный угол DАВС. (устно: найти площадь боковой поверхности пирамиды, если в основании лежит равносторонний треугольник со стороной 4, высота равна .
II. Изучение нового материала
Среди пирамид выделяют правильные пирамиды.
Что это за пирамиды? Оказывается, что это пирамиды, в основании которых лежат правильные многоугольники, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Слайд 6.
Приведите примеры правильных многоугольников. (Равносторонний треугольник, квадрат, правильный шестиугольник)
Как найти центры этих многоугольников?
(для равностороннего треугольника центр лежит в точке пересечения его медиан, высот и биссектрис , центр вписанной и описанной окружностей). Слайд 7.
(для квадрата центр лежит в точке пересечения диагоналей). Слайд 8.
(для правильного шестиугольника центр лежит в точке пересечения диагоналей). Слайд 9.
Введем еще одно определение, которое необходимо при работе с правильной пирамидой.
Апофемой называется высота боковой грани правильной пирамиды.
Рассмотрим свойства правильной пирамиды. Слайд 10.
Устно доказать некоторые из свойств, например, что боковые ребра равны и боковые грани — равные равнобедренные треугольники.
Докажем теорему о площади боковой поверхности правильной пирамиды. Слайд 11. У доски доказывает ученик.
III. Закрепление нового материала
Задача: В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 60°. Найти площадь полной поверхности пирамиды. Слайд 12.
Задача из учебника № 264 при наличии времени.
IV. Подведение итогов. Слайд 13.
V. Домашнее задание.
Прочитать параграф 2, п.29; доказать свойства правильной пирамиды; доказать теорему о площади боковой поверхности правильной пирамиды; выполнить № 257, № 259, № 264.
urok.1sept.ru