Рисунок пирамида: Линейно-конструктивный рисунок пирамиды • СПЛАЙН

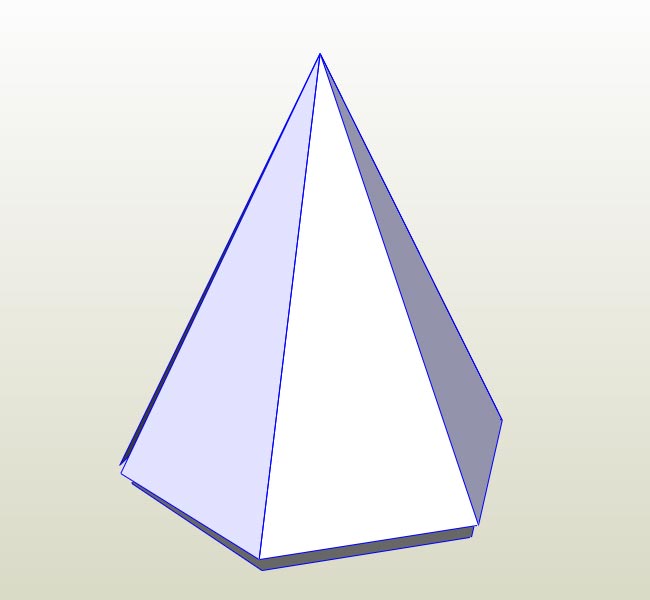
Линейно-конструктивный рисунок пирамиды • СПЛАЙН

ЦЕЛЬ ЗАДАНИЯ. Научиться изображать пирами­ду в различных положениях.
ПОСТАНОВКА ЗАДАНИЯ. Изобразите куб в уг­ловой перспективе. Постройте на каждом квадра­те основания куба вертикальные и горизонтальные
пирамиды.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите пирамиду на рис. 3.43 и ее ортого­нальные проекции на рис. 3.44. Основанием четы­рехгранной пирамиды является квадрат, ее боко­выми гранями — одинаковые треугольники. Высота пирамиды по отношению к стороне квадрата осно­вания определяет ее пропорции (высокая или при­земистая).

Начинать построение стоящей пирамиды необ­ходимо с изображения квадрата основания. Через точку пересечения его диагоналей проведите вер­тикаль, на которой отложите отрезок, равный высо­те пирамиды (рис. 3.45). Соединив полученную та­ким образом вершину пирамиды с вершинами квад­рата основания, получим перспективный рисунок четырехгранной пирамиды (рис. 3.

46). Построение пирамиды с вертикальным квадратом основания ве­дется в той же последовательности.

Сечения пирамиды плоскостями, параллельными основанию, — квадраты, размеры которых зависят от положения секущей плоскости — ближе к вершине пирамиды размер сечений меньше, чем у основания (рис. 3.47). Сечение, перпендикулярное основанию пирамиды, проходящее через ее вершину и среднюю линию квадрата основания, представляет собой тре­угольник. Все другие сечения пирамиды, параллель­ные этому — трапеции, большее основание которых равно стороне квадрата основания, меньшее — меня­ется в зависимости от положения плоскости сечения (рис. 3.48). При построении таких сечений помните, что боковые стороны трапеций параллельны высо­там в треугольниках боковых граней.

Теперь, когда вы хорошо изучили последова­тельность построения пирамиды и ее сечения плос­костями различного направления, приступайте к выполнению основного задания. Нарисуйте куб (рис. 3.49). Пересеките диагонали всех шести граней куба и проведите прямые, соединяющие центры противолежащих квадратов.

Отложите на этих пря­
мых высоты пирамид (рис. 3.50). Все шесть пира­мид одинаковы по высоте (1,5 а, где а — ребро куба), но на рисунке их высоты имеют разные размеры.

Для определения высот пирамид разного положе­ния в качестве единицы измерения используются различные отрезки. Так, например, при определе­нии высот вертикальных пирамид такой единицей измерения является отрезок вертикальной прямой, ограниченный точками центров горизонтальных граней куба. Для высот горизонтальных пирамид та­кими единицами являются отрезки прямых, прохо­дящие через центр куба и имеющие то же направ­ление, что и определяемая высота. Таким образом, в любом рисунке, основу которого составляют гео­метрические тела, куб выступает в роли трехмерной линейки, при помощи которой можно определить или измерить длины отрезков, лежащих в трех вза­имно перпендикулярных направлениях. Определяя точки вершин пирамид, учитывайте также перспек­тивные сокращения отрезков. Соедините вершины всех шести пирамид с вершинами квадратов осно­ваний (рис.

3.51).

Какие макеты рисунков SmartArt имеют неограниченное количество фигур?

Процесс со смещением		Неограниченное.
Переменный поток		Неограниченное.
Лента со стрелками		Максимум две идеи.
Простой ломаный процесс		Неограниченное.
Простой уголковый процесс		Неограниченное.
Простой процесс		Неограниченное.
Простая временная шкала		Неограниченное.
Уголковый список		Неограниченное.
Круглый ломаный процесс		Неограниченное.
Закрытый уголковый процесс		Неограниченное.
Стрелка непрерывного процесса		Неограниченное.
Непрерывный блочный процесс		Неограниченное.
Сходящиеся стрелки		Неограниченное.
Расходящиеся стрелки		Неограниченное.
Уравнение		Неограниченное.
Воронка		Не более трех идей в воронке и четвертая под ней.
Шестеренки		Одна основная идея и две зависимые идеи. Текст третьего уровня также показан.
Противостоящие стрелки		Две идеи.
Процесс со смещенными рисунками		Неограниченное.
Стрелки процесса		Неограниченное.
Список процессов		Неограниченное.
Повторяющийся ломаный процесс		Неограниченное.
Ступенчатый процесс		Не более пяти фигур.
Восходящая стрелка		Не более пяти фигур.
Вертикальный ломаный процесс		Неограниченное.
Вертикальное уравнение		Неограниченное.
Вертикальный процесс		Неограниченное.

%d0%bf%d0%b8%d1%80%d0%b0%d0%bc%d0%b8%d0%b4%d0%b0 PNG, векторы, PSD и пнг для бесплатной загрузки

Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов

4167*4167

поп арт 80 х патч стикер

3508*2480

80 основных форм силуэта

5000*5000

Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации

4167*4167

поп арт 80 х патч стикер

3508*2480

Мемфис бесшовные модели 80 х 90 х стилей

4167*4167

мемфис бесшовной схеме 80s 90 все стили

4167*4167

поп арт 80 х патч стикер

2292*2293

поп арт 80 х патч стикер

3508*2480

диско дизайн в стиле ретро 80 х неон

5556*5556

80 е брызги краски дизайн текста

1200*1200

аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс

5000*5000

поп арт 80 х патч стикер

3508*2480

скейтборд в неоновых цветах 80 х

1200*1200

Мемфис бесшовные модели 80 х 90 х стилей

4167*4167

Комплекс витаминов группы В капсулы В4 на прозрачном фоне изолированные 3d визуализации

2000*2000

Ретро музыка вечеринка 80 современный стиль искусства слова

1200*1200

поп арт 80 х патч стикер

2292*2293

поп арт 80 х патч стикер

3508*2480

Ретро стиль 80 х годов вечеринка арт дизайн

1200*1200

поп арт 80 х патч стикер

3508*2480

80 лет юбилей красный шар вектор шаблон дизайн иллюстрация

4167*4167

Неоновый эффект 80 х годов Ретро вечеринка арт дизайн

1200*1200

Элементы рок н ролла 80 х

1200*1200

ретро стиль 80 х годов диско дизайн неон плакат

5556*5556

Персонаж из партии 80 х годов

1200*1200

поп арт 80 х патч стикер

3508*2480

Трехмерная ретро игра в стиле 80 х арт дизайн

1200*1200

номер 80 золотой шрифт

1200*1200

Модель буквы м в стиле 80 х

1200*1200

80 летний юбилей дизайн шаблона векторные иллюстрации

4083*4083

поп арт 80 х патч стикер

2292*2293

поп арт 80 х патч стикер

3508*2480

буква bc 3d логотип круг

1200*1200

начальная буква bf с логотипом

1200*1200

Ретро ТВ игра 80 х годов в стиле арт дизайн

1200*1200

80 х годов ретро слово градиент цвета искусства

1200*1200

80 х годов поп арт мультфильм радуга стикер

2000*2000

Ретро мода неоновый эффект 80 х тема художественное слово

1200*1200

80 е в стиле ретро ​​мода цвет градиент арт дизайн

1200*1200

80 летие векторный дизайн шаблона иллюстрация

4167*4167

Рождество 80 х годов ретро пиксель

9449*5315

в эти выходные только мега продажи баннер скидки до 80 с

10418*10418

80 3d текст

2480*2480

сложный современный дизайн логотипа с биткойн символами и буквами bc

8331*8331

капсулы или пилюли витамина b4 диетические

2000*2000

предкрылки в стиле ретро 80 ​​с

1200*1200

ТВ игра 80 х неоновый эффект слово дизайн

1200*1200

ретро 80 х годов стиль текста эффект макет

3000*3000

80 е этап пиксель ретро диско танцы неоновые иллюстрации обои

4724*2657

Урок.

Конспект. Понятие «графика». Рисунок цилиндра, пирамиды. Штриховка

Тема: Понятие «графика». Рисунок цилиндра, пирамиды. Штриховка

Рисунок это графическое изображение окружающего мира и вместе с этим основа всех видов изобразительного искусства.

Графика это вид изобразительного искусства ( в переводе с греческого означает – письменный, пишу, черчу, рисую.)

В качестве основных изобразительных средств используются линии, штрихи, пятна и точки.

Штрихи бывают длинными и короткими, толстыми и тонкими, прямыми наклонными, извилистыми, перекрестными

С помощью штрихов художники передают форму, объем, тень и пространство,

Сначала рисунок выполняется слабыми штрихами, допускающими уточнения и исправления

Тон

Необходимого оттенка можно добиться при определенном нажиме карандаша на бумагу, чем больше нажим тем темнее тон, чем меньше -тем светлее

Свет – поверхность, на которую падают прямые лучи. Блик – самое светлое место на плоскости. Полутень – поверхность или плоскость, освещённая косыми скользящими лучами света. Собственная тень – образуется на поверхности, куда лучи света не попадают. Падающая тень – тень падающая на лежащее пространство от предмета (она имеет форму предмета от которого отражается). Рефлекс – отражение от другого предмета. . 

Цилиндр – это геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме кругов и одной, образующей форму поверхности. Для того чтобы лучше разобраться и понять конструктивную основу строения формы цилиндра, рассмотрим рисунок.

Цилиндр.

1.Начинать работу необходимо с компоновки предмета в формате.

Лист бумаги необходимо располагать в соответствии с характером предмета, определить композиционный центр.

2.После того, как намечено расположение цилиндра, приступаем к конструктивному построению, соблюдая законы линейной перспективы. Изображение следует начинать с построения его основания. Ширина нижнего эллипса относительно верхнего, должна быть чуть больше.

3. При конструктивном построении уже можно показать пространство, с помощью утолщения линии на более близких частях предмета.

4.По окончании работы над построением цилиндра, необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2 – 4 метров, в зависимости от размера рисунка.

5.Далее необходимо выявить объем цилиндра светотенью – тоном. Для этого необходимо определить самые светлые и самые темные места в натуре. А также необходимо проследить направление световых лучей, падающих на поверхность предмета. Определив границы света и теней на цилиндре, находим положение падающих теней. Затем приступаем к прокладке тона.

6.Тон следует прокладывать постепенно, начиная от самых темных мест, одновременно по всему участку рисунка, при этом сопоставляя силу тонов, по отношению друг к другу и в целом, в том числе, учитывая силу тона фона.

7.Моделируя форму, очень важно работать тоновыми отношениями, начиная от самого светлого до самого темного и их промежуточных тонов ( блик, свет, полутень, тень). Чтобы правильно взять тоновые отношения, следует исходить от натуры, от двух противоположных по силе контрастных пятен на ней. Самым светлым местом натуры будет блик и его окружение, а самое темное – собственная и падающая тени. Эти два контрастных пятна должны служить ориентиром в последующей работе над светотональным рисунком при определении правильных тоновых отношений.

1.Задание: Сделать рисунок цилиндра. (Выполнить построение цилиндра и проложить светотеневую штриховку.)

2.Задание: Сделать рисунок пирамиды. (Выполнить построение пирамиды и проложить светотеневую штриховку.)

Пирамида – многогранник, основание которого представляет собой многоугольник или треугольник, а боковой грани – треугольники, имеющие общую вершину.

Пирамида потребностей проекта или ПроектING / Хабр

На примере пирамиды развития коммерческой организации.

В первую очередь предлагаемая пирамида является инструментом менеджера по развитию проекта. Данный инструмент позволяет разложить все по полочкам, планировать и контролировать исполнение задач развития и/или жизненного цикла проекта. Пирамида потребностей проекта позволяет оценить основные точки развития проекта и связать при помощи них задачи и время на их реализацию.

Пирамида потребностей проекта – это инструмент позволяющий выделить основные потребности для реализации проекта. Удовлетворение каждой потребности позволяет проекту функционировать в заданных этой потребностью рамках. Так же каждая удовлетворенная потребность открывает для проекта новую точку роста и позволяет выявить следующую потребность. Пирамида потребностей охватывает проект с внешней стороны, позволяет разделить проект на группы задач по уровню сложности и получаемой от их реализации ценности.

Пирамида потребностей проекта (или компании) визуально похожа на пирамиду потребностей человека по Маслоу, но только визуально. В отличии от пирамиды потребностей человека, пирамида потребностей проекта разрабатывается под каждый проект отдельно (она индивидуальна) и может изменяться исходя из краткосрочных и долгосрочных прогнозов развития, внешних и внутренних факторов. Так же переход от одной потребности к другой не означает, что предыдущая потребность была удовлетворена полностью, так как в проектной деятельности, как известно, нет предела совершенствованию.

Я предлагаю рассматривать компанию как организм, с четкой структурой, потребностями и планом действий по их удовлетворению, которые возникают по ходу развития, роста и последующего угасания или нового витка роста.

Расположение потребностей в пирамидальной форме было выбрано не случайно. У пирамиды и процесса развития проекта очень много схожего. Пирамида визуально стремится вверх, как и проект всегда стремится вверх, к развитию. Пирамида строится постепенно, поэтапно, каждый этап связан с определенными сложностями. Так же новый этап не возможен без создания предыдущего. Пирамида – это одновременно и сложное строение и отличный визуализатор, поэтому расположение потребностей проекта пирамидой поможет показать одновременно и сложности, с которыми столкнутся люди при реализации, и этапы и результат, который будет достигнут.

Пирамида потребностей проекта – это пирамида состоящая минимум из семи групп потребностей (рисунок 1). Не обязательно все эти группы потребностей будут использоваться в каждом проекте, в данной пирамиде указано идеальное расположение потребностей. Но каждая коммерческая структура для роста нуждается в удовлетворении всех указанных на рисунке потребностей.

Из пирамиды потребностей проекта вытекает древовидная система проекта (рисунок 2), которая в дальнейшем буден перенесена в удобный инструментарий для реализации (например, в диаграмму Ганта).

*Рисунок 1. Пирамида потребностей проекта

* Рисунок 2. Древовидная система потребностей проекта

Разработка пирамиды потребностей проекта на данный момент актуальна тем, что в период стагнации и кризисных явлений позволяет четко определить актуальные направления развития проекта, инвестиции, которые следует поддерживать. А так же те потребности, которые следует приостановить или отложить до тех пор, пока предшествующие потребности не будут удовлетворены. Так же пирамида потребностей может визуализировать актуальные и не удовлетворённые потребности, которые в ближайшем времени помогут проекту улучшить свое положение. Так сказать структурировать точки роста и увидеть потенциал для развития.

Компания на начальном этапе живет теми потребностями, которые ставят перед ней собственники и рынок. Чаще всего это те потребности, которые позволяют компании просто выживать. Не расти, не развиваться, а именно выживать. То есть компания удовлетворяет только жизненно важные потребности – в покупке товара, оборудования, найме только ключевых работников. С последующим ростом компании, укреплении и в максимальном удовлетворении первичных потребностей появляются новые потребности. Чаще всего компания перерастает старые потребности. Первичные потребности уже не позволяют компании вырасти.

Тут как раз и кроется краеугольные камень данного подхода, который показывает, что для роста компании требуется рост потребностей и их удовлетворение. При неудовлетворении потребностей роста не будет. Так же при росте, взрослении, компания может постепенно отходить от первичных потребностей к потребностям более высокого значения. При этом более низкие потребности просто будут отвергнуты и перестанут играть сначала ключевую, а в дальнейшем и какую либо роль в развитии.
Так же не маловажно понимать, что даже удовлетворение только первичных потребностей дает проекту шанс на выживание. То есть не обязательно, что проекту понадобится удовлетворять какие-то более высокие по иерархии потребности. Но если проект не удовлетворяет последовательно потребности, он закрывает себе возможность для роста дохода.

Так, например, потребность в продвижение при помощи газетной рекламы в начале 2000 годов уступила место продвижению при помощи Интернет рекламы. Уступила безвозвратно, и выросшие компании из 90 переступили через эту потребность.
Вот и в кризис, для экономии компания может сокращать свои потребности, начиная с высших, экономя на росте. Или наоборот, отвергая низшие, менее эффективные потребности.
Давайте рассмотрим потребности проекта снизу вверх. В качестве проекта я рассматриваю работу коммерческой и общественной организации.

Первичные потребности или протопротребности. Эти потребности возникают у проекта в самом начале его становления. В первую очередь, потребности в инвестициях. Данный вид потребностей потянет за собой, как за магнитом, все остальные потребности. При этом чаще важны не столько денежные инвестиции, сколько инвестиции времени, энергии и умственные. Эта потребность основная, если не выполнить все первичные потребности проект в дальнейшем начнет пробуксовывать и рано или даст сбой.

Потребности экстенсивного роста. Данные потребности вбирают в себя основные потребности, которые нужно удовлетворить проекту для своего выживания в начальный период своего существования. Чаще всего эти потребности удовлетворяют максимально экономными и в тоже время проверенными, не требующими сложного исполнения и особого навыка, действиями. Потребности экстенсивного роста подразумевают под собой минимальный креатив. В большей степени эти потребности удовлетворяются проверенными инструментами, скопированными и апробированными в других проектах.

Потребности организационного изменения. Период изучения и аналитики проделанной работы, подведения итогов, осмысления уровня удовлетворения потребностей и появляющихся новых потребностей. Это важный и сложный момент, так как с ростом потребностей проект требует все более профессионального, логически выверенного подхода. Удовлетворение данной потребности повлечёт за собой переход на новый компетентный уровень, использование более сложных инструментов и в итоге гарантирует получения большего результата. Эта потребность требует профессионального и опытного творчества, креативного подхода, своего взгляда на мир и проект. Чаще всего, на этом этапе вносятся улучшения в существующие и действующие процессы проекта.

Потребности интенсивного роста. За организационными изменениями, когда проект подготавливает себя к дальнейшему развитию, наступает потребность в интенсивном росте, когда проект использует предыдущие наработки для получения более качественного и востребованного продукта. Для удовлетворения этой потребности требуется подготовленные и образованные специалисты, готовые при помощи своего опыта и знаний развивать проект в новых направлениях. Так же для удовлетворения этой потребности, скорее всего, понадобятся новые, крупные, инвестиции в проект. На этом этапе вносятся в проект новые процессы, которые оправдали себя в аналогичных проектах, но по каким либо причинам были дороги на предыдущих этапах удовлетворения потребностей. На этом этапе происходит работа над теми задачами, которые были поставлены при удовлетворении предыдущей потребности.

Потребности фундаментального изменения. Чаще всего на этом этапе вносятся в проект обдуманные и скорректированные, абсолютно новые процессы. Эти новейшие процессы, до этого момента, мало использовались или совершенно не использовались в аналогичных проектах. Эти процессы в дальнейшем будут кардинально изменять или дополнять продукт и проект в целом, в конечном счете, дополняя его максимальной ценностью.

Потребности стратегического роста. Эта потребность на первый взгляд схожа с потребностью интенсивного роста. Но в отличии от потребности интенсивного роста, эта потребность удовлетворяется максимально индивидуальными методами и инструментами. Именно на этом этапе происходит исполнение тех задач, которые были поставлены перед проектом при удовлетворении потребности в фундаментальных изменениях.

Высшие потребности. Под высшими потребностями мы будем понимать, те потребности, которые находятся за горизонтом планирования. Мы уверены, что эти потребности у нас появятся, при условии, что все прочие потребности будут удовлетворены, мы даже можем их озвучить. Но высшие потребности настолько далеки или точно не ясно, какие же точно из них появятся у проекта, что они находятся за горизонтом планирования. Такими потребностями в конечно случае могут быть, например, создание региональных представительств, выход на иностранный рынок и прочее. То есть эти потребности очень большие и рассматриваются только по достижению потребностей находящихся ниже по иерархии.

Так же следует отметить, что рост потребностей обуславливается и тем, что потребности находящиеся в вверху пирамиды приносят большую выгоду проекту. Поэтому стремление к более высоким потребностям является мотивирующим фактором для проекта. Но так же стоит учитывать и то, что более высокие потребности требуют большей энергии и затрат.

Основные затраты (инвестиции) на удовлетворение потребностей:
• Здоровье (не восполняемая)
• Образование (восполняемая)
• Жизненная энергия (не восполняемая)
• Время (не восполняемая)
• Деньги (восполняемая)

Данные затраты присутствуют при удовлетворении каждой потребности но их процентная составляющая в удовлетворении потребностей разная и зависит от индивидуальных особенностей проекта, потребностей и людей. Помимо этого данные затраты делятся на затраты восполняемые и не восполняемые. Следовательно, следует внимательно относится к распределению затрат на реализацию проекта и максимально логично продумывать удовлетворение каждой потребности.

При визуальном оформлении пирамиды потребностей, происходит деление проекта на этапы (потребности). Каждый этап – это потребность и одно деление пирамиды. При этом, каждая потребность характеризуется несколькими принципами:

• Реальность. Потребность реально можно удовлетворить, то есть довести до ощутимого результата. Потребности удовлетворяются по заранее подготовленному плану.
• Логичность. Сами потребности и процесс их удовлетворения выстроены в логическую цепочку, отвечающую здравому смыслу и видению развития проекта.
• Время. У удовлетворения потребности есть начало, точное время потраченное на удовлетворения и конец. Мы точно знаем, сколько нам понадобится времени на удовлетворения потребности.
• Перспектива. В начале, середине или конце выполнения работы над проектом, мы начинаем видеть перспективу будущего развития проекта. Мы начинаем чувствовать то, что нам не хватает, у проекта появляются новые потребности. Эти новые потребности вытекают в новое делении пирамиды.

Приведем несколько примеров.
В качестве первого примера возьмем магазин по продаже одежды. Это магазин в торговом центре средней руки, четыре продавца, администратор, десяток поставщиков. Мы рассматриваем магазин как бизнес, нацеленный на получение прибыли для своих учредителей. У такого магазина, будет ряд потребностей. Первичные потребности, потребности экстенсивного роста, потребности организационного роста, потребности интенсивного роста, потребности стратегического роста, высшие потребности.

Грубо, пирамида будет выглядеть так:
• Потребность интенсивного роста. Проводить тренинги по продажам, знанию товара для персонала. Оптимизировать представленность товара в зале. Пересмотр сетки заказа товара. Создать программу акций и распродаж. Поиск и прием на работу администратора. Ввод системы показателей эфективности магазина:

• Потребность организационного изменения. Плохо работает персонал, нужны изменения. Большие товарные остатки, плохо продаются. Постоянно опаздывают продавцы.

• Потребность в экстенсивном росте. Следить за работой персонала, за чистотой в зале. Вывешивать все модели товара зале. Вовремя закрывать и открывать магазин. Создать подарочные карты. Ввести дисконтные карты.

• Протопотребности. Определить бюджет на открытие магазина найти площадь. Заключить контракт на аренду. Нанять персонал. Заключить договора на поставку товара. Разработать дизайн, сделать ремонт. Смонтировать оборудование.

Так может выглядеть пирамида потребностей проекта по развитию магазина одежды.

Давайте рассмотрим следующий пример. Компания занимается выпуском строительного оборудования. Продажи строятся через сеть интернет и немногочисленных дистрибьюторов. Своего производства нет, все производство находится на аутсорсинге.
• Потребность интенсивного роста. Доработать пульт управления станком. Заказать несколько эскизов оборудования агентству промышленного дизайна. Нанять секретаря. Снять несколько видеороликов для презентации продукции, сделать профессиональные фото продукции. Получить сертификаты на станки. Принять участие в нескольких отраслевых выставках. Провести тренинг по развитию, возможно нанять маркетолога.

• Потребность организационного изменения. Станок не показывает нужной производительности. Дизайн оборудования устарел. Не успеваем оформлять все документы, делаем ошибки. Клиенту не хватает информации на сайте. Мало доверия к продукции, приходится дольше убеждать клиентов. Требуется мониторинг рынка, нужно следить за конкурентами, искать новинки.

• Потребность в экстенсивном росте. Заказать больше видов оборудования. Расширить рекламную компанию в Интернете. Заключить договор на несколько новых номеров телефонов в офис.

• Протопотребности. Снять офис. Нанять персонал на склад и в офис. Найти изготовителя. Создать интернет сайт. Подписать договора с поставщиками комплектующих для станков.

Как видно из примеров потребности делятся по сложности и нужности, располагаются пирамидой и удовлетворяются друг за другом. Каждая новая потребность вытекает из предыдущей удовлетворенной потребности. На каждом этапе удовлетворения потребности можно остановиться, но тогда есть риск, что проект не принесет желаемого результата и фирма постепенно скатится в стагнацию.

Уверен, что пирамида потребностей проекта, будет успешно применяться в качестве инструмента планирования развития компании. Пирамида потребностей помогает разложить этапы проекта на основные составляющие, увидеть перспективу развития.

Жду критику и отзывы.

Объем пирамиды

А пирамида является многогранником с одним основанием, которое является произвольным многоугольник . Остальные его грани — треугольники.

В объем из 3 -размерное твердое тело — это объем занимаемого пространства. Объем измеряется в кубических единицах ( в 3 , футов 3 , см 3 , м 3 и так далее).Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.

Громкость V пирамиды составляет одну треть площади основания B раз больше высоты час .

V знак равно 1 3 B час

Пример:

Найдите объем правильной квадратной пирамиды со сторонами основания 10 см и высота 18 см.

Решение

Нарисуйте фигуру.

Формула объема пирамиды:

V знак равно 1 3 B час

Поскольку основание пирамиды представляет собой квадрат, площадь основания равна 10 2 или 100 см 2 .

Итак, заменим 100 для B а также 18 для час в формуле.

V знак равно 1 3 ( 100 ) ( 18 ) знак равно 600

Следовательно, объем квадратной пирамиды равен 600 см 3 .

Пирамиды

Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .

На самом деле это Квадратные пирамиды , потому что их основание — Квадрат.

Части пирамиды

Пирамида создается путем соединения основания с вершиной

Основание — многоугольник (плоский с прямыми краями), а все остальные грани — треугольники.Никаких кривых!

Виды пирамид

Есть много типов пирамид, и они названы в честь формы их основания.

Пролетите здесь через пирамиды.

Правая и наклонная пирамида

Это говорит нам, где находится вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правая пирамида , в противном случае — наклонная пирамида .

Правая пирамида	Наклонная пирамида

Обычная пирамида и неправильная пирамида

Это говорит нам о форме основания .Когда основание представляет собой правильный многоугольник, это правильная пирамида , в противном случае это неправильная пирамида .

Правильная пирамида	Неправильная пирамида
База обычная	База нестандартная

Площадь и объем

Объем пирамиды

• ¹ / ₃ × [Базовая площадь] × Высота

Площадь пирамиды

Если все боковые грани одинаковые:

• [Базовая область] + ¹ / ₂ × периметр × [наклонная длина]

Если боковые грани разные:

• [Базовая область] + [Боковая область]

Примечания к площади

Площадь поверхности состоит из двух частей: площади основания ( Площадь основания ) и площади боковых граней ( Боковая область ).

Для Базовая область :

Это зависит от формы, существуют разные формулы для треугольника, квадрата и т. Д. См. Формулы «Площадь» или наш Инструмент расчета площади

Для Боковая зона :

Когда все боковые грани одинаковые:

• Умножьте периметр на «наклонную длину» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а формула треугольника: «база, умноженная на высоту, деленную на 2»

Но когда боковые грани разные (например, «неправильная» пирамида), мы должны сложить площадь каждого треугольника, чтобы найти общую боковую площадь.

Объем пирамиды — объяснение и примеры

Пирамида — это трехмерная диаграмма , многоугольное основание которой соединено с вершиной треугольными гранями в геометрии. Треугольные грани пирамиды известны как боковые грани, а расстояние по перпендикуляру от вершины (вершины) до основания пирамиды известно как высота.

Пирамиды названы в честь формы их оснований. Например, прямоугольная пирамида имеет прямоугольное основание, треугольная пирамида имеет треугольное основание, пятиугольная пирамида имеет пятиугольное основание и т. Д.

Как найти объем пирамиды?

В этой статье мы обсудим , как найти объем пирамид с различными типами оснований и решить задачи со словами, связанные с объемом пирамиды.

Объем пирамиды определяется как количество кубических единиц, занимаемых пирамидой. Как указывалось ранее, название пирамиды происходит от формы ее основания. Поэтому объем пирамиды зависит еще и от формы основания.

Чтобы определить объем пирамиды, вам нужны только размеры основания и высота.

Объем формулы пирамиды

Общий объем формулы пирамиды определяется как:

Объем пирамиды = 1/3 x площадь основания x высота.

V = 1/3 A _b h

Где A _b = площадь многоугольного основания, а h = высота пирамиды.

Примечание: Объем пирамиды незначительно варьируется в зависимости от многоугольного основания.

Пример 1

Рассчитайте объем прямоугольной пирамиды с основанием 8 см на 6 см и высотой 10 см.

Решение

Для прямоугольной пирамиды основанием является прямоугольник.

Площадь прямоугольника = l x w

= 8 x 6

= 48 см ² .

А по объему формулы пирамиды имеем

Объем пирамиды = 1 / 3A _b h

= 1/3 x 48 см ² x 10 см

= 160 см ³ .

Пример 2

Объем пирамиды 80 мм ³ .Если основание пирамиды представляет собой прямоугольник длиной 8 мм и шириной 6 мм, найдите высоту пирамиды.

Раствор

Объем пирамиды = 1 / 3A _b h

⇒ 80 = 1/3 x (8 x 6) xh

⇒ 80 = 15.9h

Разделив обе стороны на 15,9, получаем,

h = 5

Таким образом, высота пирамиды 5 мм.

Объем квадратной пирамиды

Чтобы получить формулу объема квадратной пирамиды, заменим площадь основания (A _b ) на площадь квадрата (Площадь квадрата = a ² )

Следовательно, объем квадратной пирамиды определяется как:

Объем квадратной пирамиды = 1/3 xa ² xh

V = 1/3 a ² h

Где a = длина стороны основания (квадрат) и h = высота пирамиды.

Пример 3

Квадратная пирамида имеет длину основания 13 см и высоту 20 см. Найдите объем пирамиды.

Решение

Дано:

Длина основания, a = 13 см

высота = 20 см

Объем квадратной пирамиды = 1/3 a ² h

При подстановке имеем,

Объем = 1/3 x 13 x 13 x 20

= 1126,7 см ³

Пример 4

Объем квадратной пирамиды составляет 625 кубических футов.Если высота пирамиды 10 футов, каковы размеры основания пирамиды?

Раствор

Дано:

Объем = 625 кубических футов.

высота = 10 футов

По объему квадратной формулы

⇒ 625 = 1/3 a ² h

⇒ 625 = 1/3 xa ² x 10

⇒ 625 = 3,3a ²

⇒ a ² = 187,5

⇒ a = = √187,5

a = 13,7 футов

Итак, размеры основания будут 13.7 футов на 13,7 футов.

Пример 5

Базовая длина квадратной пирамиды в два раза больше высоты пирамиды. Найдите размеры пирамиды, если она имеет объем 48 кубических ярдов.

Решение

Пусть высота пирамиды = x

длина = 3x

объем = 48 кубических ярдов

Но объем квадратной пирамиды = 1/3 a ² h

Заменить .

⇒ 48 = 1/3 (3x) ² (x)

⇒ 48 = 1/3 (9x ³ )

⇒ 48 = 3x ³

Разделите обе части на 3, чтобы получить,

⇒ x ³ = 16

⇒ x = ³ √16

x = 2.52

Следовательно, высота пирамиды = x ⇒ 2,53 ярда,

и каждая сторона основания равна 7,56 ярда

Объем трапециевидной пирамиды

Трапециевидная пирамида — это пирамида, основание которой представляет собой трапецию или трапецию. .

Поскольку мы знаем, площадь трапеции = h ₁ (b ₁ + b ₂ ) / 2

Где h = высота трапеции

b ₁ и b ₂ являются длины двух параллельных сторон трапеции.

Учитывая общую формулу объема пирамиды, мы можем вывести формулу объема трапециевидной пирамиды как:

Объем трапециевидной пирамиды = 1/6 [h ₁ (b ₁ + b ₂ )] H

Примечание: При использовании этой формулы всегда помните, что h — высота трапециевидного основания, а H — высота пирамиды.

Пример 6

Основание пирамиды представляет собой трапецию с параллельными сторонами длиной 5 м и 8 м и высотой 6 м.Если пирамида имеет высоту 15 м, найдите объем пирамиды.

Решение

Дано;

h = 6 м, H = 15 м, b ₁ = 5 м и b ₂ = 8 м

Объем трапециевидной пирамиды = 1/6 [h ₁ (b ₁ + b ₂ )] h

= 1/6 x 6 x 15 (5 + 8)

= 15 x 13

= 195 м ³ .

Объем треугольной пирамиды

Как известно, площадь треугольника;

Площадь треугольника = 1/2 b h

Объем треугольной пирамиды = 1/3 (1/2 b h) H

Где b и h — длина основания и высота треугольника.H — высота пирамиды.

Пример 7

Найдите площадь треугольной пирамиды с площадью основания 144 дюйма, ² и высотой 18 дюймов.

Решение

Дано:

Площадь основания = 144 дюйма ²

H = 18 дюймов

Объем треугольной пирамиды = 1/3 (1/2 bh) H

= 1/3 x 144 x 18

= 864 дюйма ³

Практика Задачи

1. Каков объем пирамиды высотой 12 единиц с прямоугольным основанием размером 8 единиц на 9 единиц?
2. Рассмотрим пирамиду с основанием равнобедренного треугольника с двумя сторонами длиной 14 единиц каждая и 16 единиц.Найдите объем пирамиды, если ее высота 22 единицы.
3. Рассмотрим пирамиду с квадратным основанием по 11 см каждая. Если объем этой пирамиды 520 см ³ , какова высота этой пирамиды?

Предыдущий урок | Главная страница | Следующий урок

Пирамиды, призмы, цилиндры и конусы (предалгебра, площадь и объем) — Mathplanet

Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела.Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.

Объем — это мера того, сколько может вместить фигура, и измеряется в кубических единицах. Объем говорит нам кое-что о вместимости фигуры.

Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть как прямоугольные, так и треугольные призмы.

Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем твердое тело, как картонную коробку, и расплющиваем его, чтобы найти все включенные геометрические формы.

Чтобы найти объем призмы (не имеет значения, прямоугольная она или треугольная), мы умножаем площадь основания, называемую площадью основания B, на высоту h.

$$ V = B \ cdot h $$

Цилиндр — это труба, состоящая из двух параллельных конгруэнтных окружностей и прямоугольника, основанием которого является окружность окружности.{2} \ cdot h $$

Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех- или четырехсторонней поверхности соответственно в основании. Когда мы вычисляем площадь поверхности пирамиды ниже, мы берем сумму площадей четырех треугольников и базового квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.

Объем пирамиды составляет одну треть объема призмы.

$$ V = \ frac {1} {3} \ cdot B \ cdot h $$

Основание конуса — круг, и это легко увидеть.Боковая поверхность конуса представляет собой параллелограмм с основанием, составляющим половину окружности конуса, и с наклонной высотой, равной высоте. Это может быть немного сложнее увидеть, но если вы разрежете боковую поверхность конуса на секции и положите их рядом друг с другом, вы легко увидите .

Площадь поверхности конуса, таким образом, складывается из площадей основания и боковой поверхности:

$$ \ begin {matrix} A_ {base} = \ pi r ^ {2} & \, \, and \, \, & A_ {LS} = \ pi rl \ end {matrix} $$

$$ A = \ pi r ^ {2} + \ pi rl $$

---

Пример

$$ \ begin {matrix} A_ {base} = \ pi r ^ {2} \: \: & \, \, and \, \, & A_ {LS} = \ pi rl \: \: \: \ : \: \: \: \\ A_ {base} = \ pi \ cdot 3 ^ {2} & & A_ {LS} = \ pi \ cdot 3 \ cdot 9 \\ A_ {base} \ приблизительно 28.{3} $$

---

Видеоуроки

Найдите объем конуса высотой 5 и радиусом 3.

---

Найти площадь поверхности цилиндра радиусом 4 и высотой 8

Правильные пирамиды

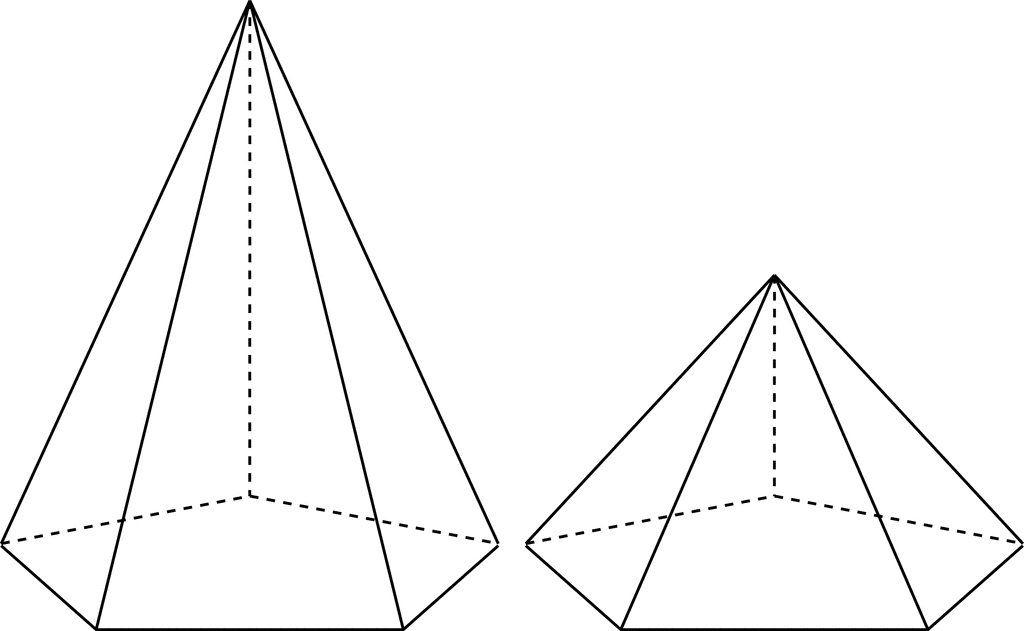
Правильная пирамида — это пирамида, основание которой представляет собой правильный многоугольник, а боковые стороны которой равны по длине. Пирамида названа по ее основанию. На рисунке показаны некоторые примеры правильных пирамид.

Рисунок 1 Некоторые различные типы правильных пирамид.

Боковые грани правильной пирамиды — равнобедренные равнобедренные треугольники. Высота любого из этих треугольников равна наклонной высоте правильной пирамиды. Рисунок 2 представляет собой квадратную пирамиду.

Рисунок 2 Квадратная пирамида.

Пирамиды также имеют боковую площадь, общую площадь и объем.

Теорема 93 : Боковая площадь, LA , правильной пирамиды с наклонной высотой l и периметром основания p определяется следующим уравнением.

Пример 1: Найдите боковую площадь квадратной пирамиды, показанной на рисунке 3.

Рисунок 3 Определение боковой площади, общей площади и объема квадратной пирамиды.

Поскольку пирамида имеет только одно основание, ее общая площадь складывается из площади боковой поверхности и площади основания.

Теорема 94: Общая площадь TA правильной пирамиды с боковой площадью LA и площадью основания B определяется следующим уравнением.

Пример 2: Найдите общую площадь правильной пирамиды, показанной на рисунке.

Основание правильной пирамиды — квадрат . A _{квадрат} = (сторона) ² . Следовательно, B = 16 ² в ² или B = 256 в ² .

Из предыдущего примера

Теорема 95: Объем V правильной пирамиды с площадью основания B и высотой h определяется следующим уравнением.

Пример 3: Найдите объем правильной пирамиды, показанной на рисунке.

Из предыдущего примера B = 256 из ² . На рисунке показано, что h = 6 дюймов

Пирамида

В геометрии пирамида — это пространственная фигура, в основе которой лежит многоугольник, а все остальные грани — треугольники. Все грани пирамиды, кроме основания, пересекаются в общей точке. Ниже приведены некоторые примеры.

Помимо геометрии, термин «пирамида» часто используется по отношению к пирамидам Египта, которые служили гробницами древнеегипетских царей. Пирамиды иногда используются в современном строительстве, например, в Лувре, известном музее Парижа.

Свойства пирамиды

Грани пирамиды, не являющиеся ее основанием, называются боковыми гранями. Количество боковых граней пирамиды равно количеству сторон ее многоугольного основания. Сегменты линии, образованные двумя пересекающимися гранями, называются ребрами.Вершины — это точки пересечения трех или более ребер. Вершина напротив основания называется его вершиной. Вершину часто называют «вершиной» пирамиды. Это также общая точка, разделяющая все боковые грани пирамиды.

У квадратной пирамиды наверху всего пять граней. Он имеет 4 боковые грани, которые представляют собой треугольники, а его основание — квадрат. У квадратной пирамиды 8 ребер и 5 вершин.

Любое поперечное сечение, параллельное основанию пирамиды, образует многоугольник, подобный основанию.

Три треугольника, заштрихованные зеленым цветом, образованные поперечными сечениями, параллельными основанию треугольной пирамиды выше, подобны (той же формы, но не того же размера) основанию пирамиды.

Классификация пирамид

Обычно мы называем пирамиду по форме ее многоугольного основания. Ниже приведены некоторые примеры.

Правая пирамида и наклонная пирамида

Если вершина пирамиды находится прямо над центром основания, это правая пирамида.В противном случае это наклонная пирамида.

Пирамида правая	Наклонная пирамида
Перпендикулярная линия от вершины пересекает основание в его центре.	Перпендикулярная линия от вершины не пересекает основание в ее центре.

Правильная пирамида

Если основание пирамиды — правильный многоугольник, это правильная пирамида.В противном случае это неправильная пирамида. Часто правильная пирамида считается правильной пирамидой.

Правильная пирамида	Неправильная пирамида
Основание квадратной пирамиды вверху представляет собой квадрат, который представляет собой правильный многоугольник.	Основание трапециевидной пирамиды выше представляет собой трапецию, которая представляет собой неправильный многоугольник.

Тетраэдр

Тетраэдр — это особая пирамида, в которой все грани представляют собой треугольники.Это единственный тип пирамиды, в которой любая из ее граней может быть основанием, а любая из ее вершин может быть вершиной.

Объем пирамиды

Объем пирамиды:

B — это площадь основания, а h — высота пирамиды, то есть расстояние от ее вершины до основания.

Пирамида

— основание, треугольники, пирамиды и высота

Пирамида — это геометрическое тело, форма которого прославилась царскими гробницами Древнего Египта. Это твердое тело, основание которого представляет собой многоугольник, а боковые грани — треугольники с общей вершиной (вершиной пирамиды).В случае египетской пирамиды Хеопса основание представляет собой почти идеальный квадрат футов ( футов) (230 м) по краю и грани треугольников, которые приблизительно равносторонние.

Пирамиды в Гизе, Египет. Фотография Дилипа Мехиа / Свяжитесь с Гизой. Фондовый рынок. Воспроизведено с разрешения автора.

Основанием пирамиды может быть любой многоугольник с тремя или более гранями, а имена пирамид соответствуют количеству ребер в основании. Когда основание представляет собой треугольник, пирамида представляет собой треугольную пирамиду.Он также известен как тетраэдр , поскольку, включая основание, он имеет четыре грани. Когда эти грани представляют собой равносторонние треугольники, это квадратная пирамида, в основе которой лежит квадрат.

Наиболее часто встречающиеся пирамиды — это «правильные» пирамиды. Они имеют правильный многоугольник в качестве основания и равнобедренные треугольники для боковых сторон. Однако не все пирамиды правильные.

Высоту пирамиды можно измерить двумя способами: от вершины по линии , перпендикулярной к основанию, и от вершины по линии, перпендикулярной одному из краев основания.Последняя мера называется наклонной высотой. Однако, если боковые грани не являются конгруэнтными треугольниками, наклонная высота может варьироваться от грани к грани и не будет иметь большого значения для пирамиды в целом. Если слово наклон не включено, термин высота (или высота) относится к высоте.

Если помимо конгруэнтности боковые грани равнобедренные, пирамида будет правильной. В правильной пирамиде прямоугольных треугольников можно найти в изобилии. Предположим, у нас есть правильная пирамида с высотой VC и наклонной высотой VD.Здесь треугольники VCD, VDE, VCE и CDE являются прямоугольными. Если в любом из этих треугольников известны две стороны, можно использовать теорему Пифагора , чтобы вычислить третью. Это, в свою очередь, может быть использовано в других треугольниках для определения еще других неизвестных сторон. Например, если правильная квадратная пирамида имеет наклонную высоту в две единицы и основание из двух единиц на краю, боковые края должны быть √5 единиц, а высота √3 единиц.

Существуют формулы для вычисления боковой и общей площади некоторых специальных пирамид, но в большинстве случаев проще вычислить площади различных граней и сложить их.

Объем — другое дело. Вычислить объем без формулы может быть очень сложно. К счастью, существует довольно примечательная формула, возраст которой насчитывает не менее 2300 лет.

В предложении 7 книги XII своих элементов Евклид показал, что «Любая призма , имеющая треугольное основание, делится на три равные друг другу пирамиды с треугольными основаниями». Это означает, что каждая из трех пирамид, на которые была разделена призма, имеет треть объема призмы.Поскольку объем призмы равен площади, B, ее основания, умноженной на высоту, h: объем пирамиды составляет одну треть от этого, или Bh / 3.