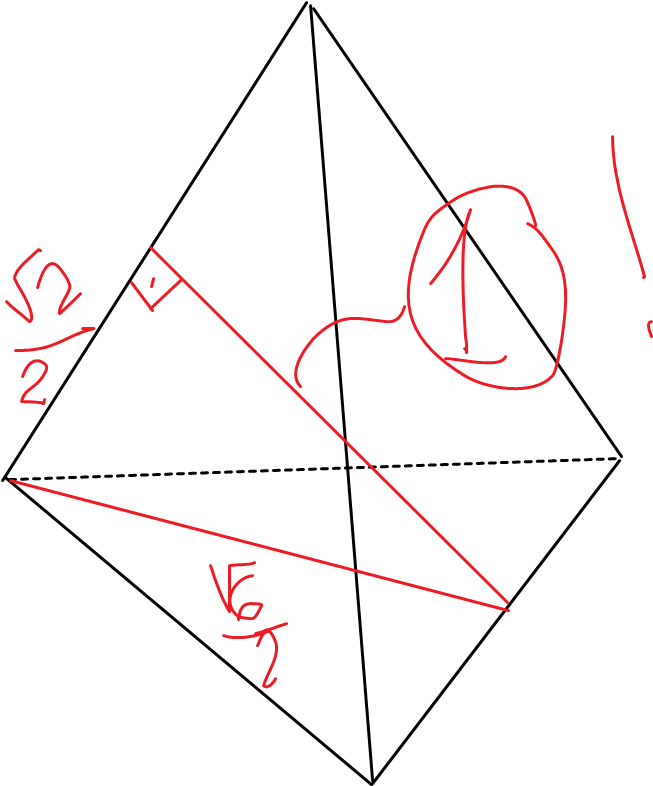
Как правильно рисовать тетраэдр
Тетраэдр — это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Типы тетраэдров.
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр — это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
— Равногранный тетраэдр, у него каждая грань представляет собой треугольник.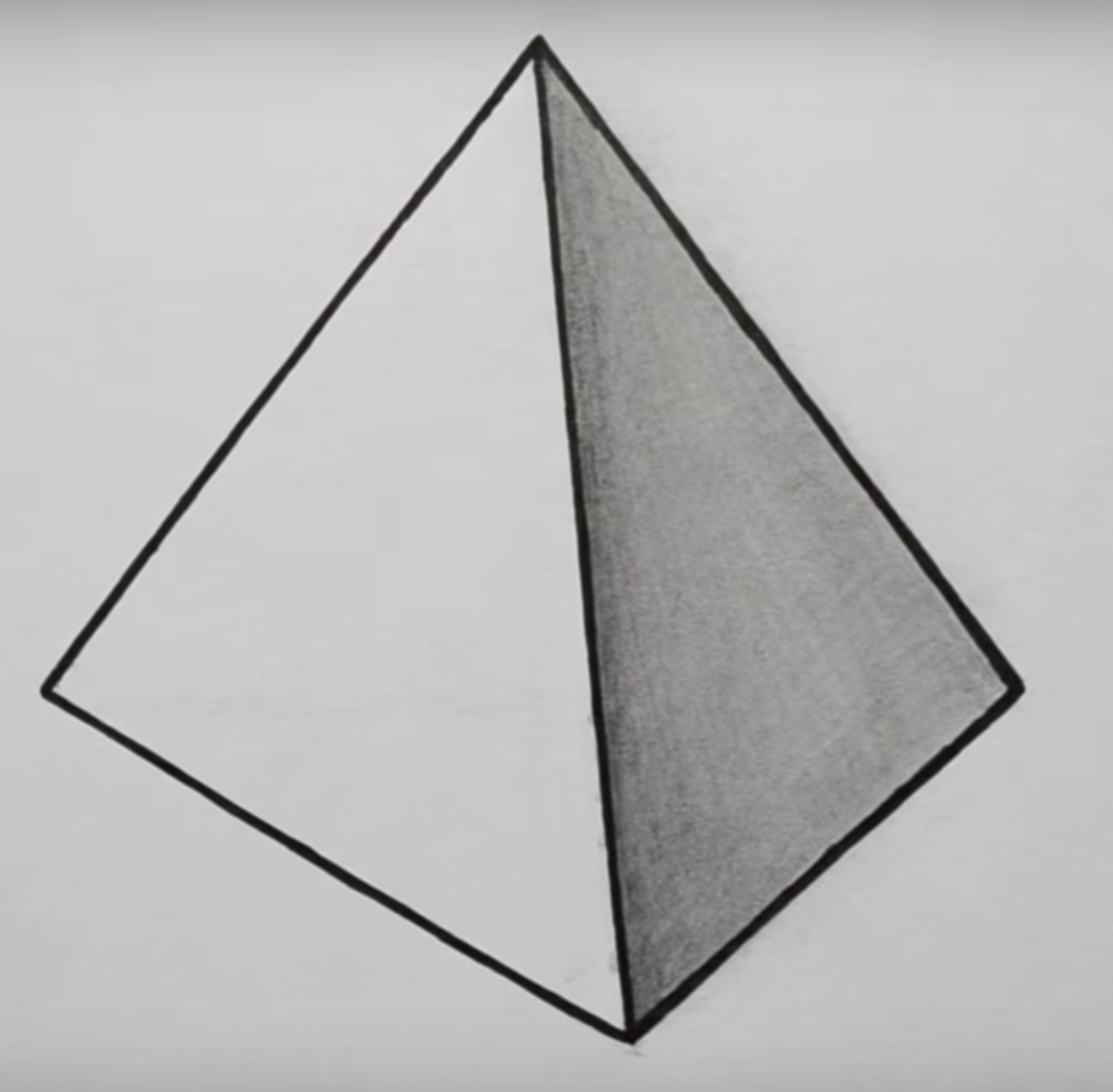 Все грани-треугольники такого тетраэдра равны.
Все грани-треугольники такого тетраэдра равны.
— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
— Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
— Соразмерный тетраэдр, бивысоты у него одинаковы.
— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Формулы для определения элементов тетраэдра.
Высота тетраэдра:
где h — высота тетраэдра, a — ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
где V — объем тетраэдра, a — ребро тетраэдра.
Основные формулы для правильного тетраэдра:
Где S — Площадь поверхности правильного тетраэдра;
h — высота, опущенная на основание;
r — радиус вписанной в тетраэдр окружности;
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».
Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.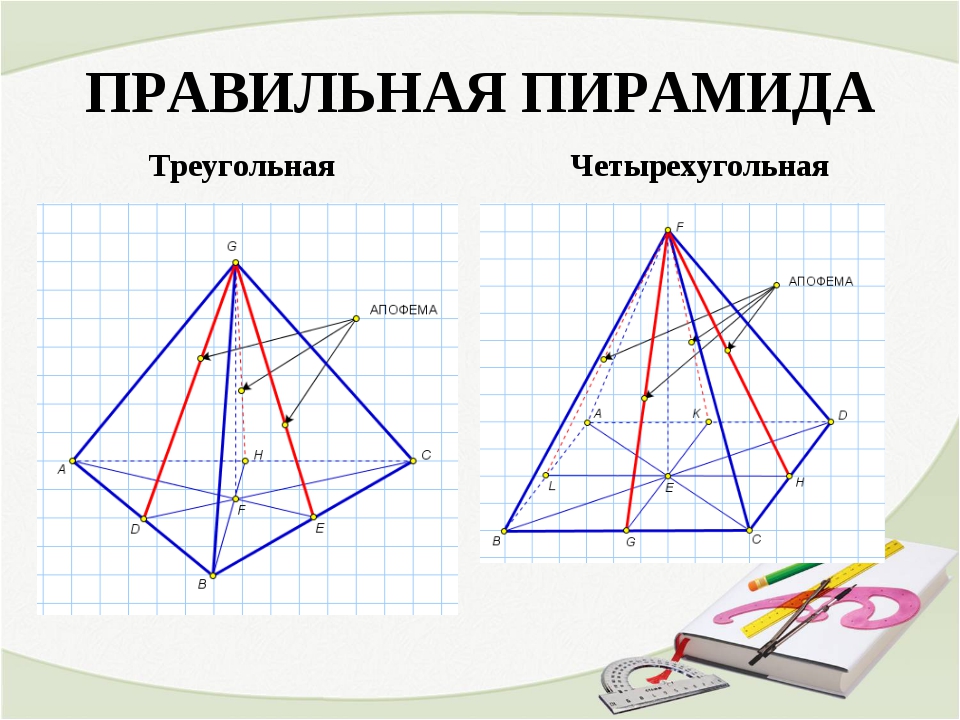
А именно о тетраэдре.
Проводить изучение многогранников будем по плану:
1. определение тетраэдра
2. элементы тетраэдра
3. развертка тетраэдра
4. изображение на плоскости
1. построим треугольник АBC
2. точка D, не лежащая в плоскости этого треугольника
3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.
Сколько граней, ребер и вершин имеет тетраэдр?
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.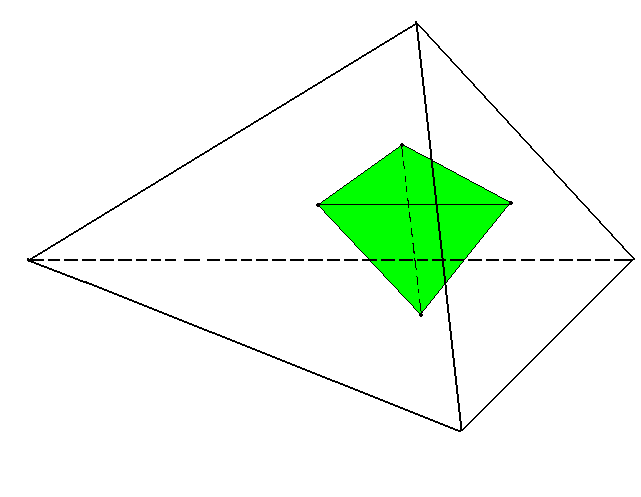
Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,
ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.
На плоскости тетраэдр изображается
В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.
На первом рисунке AC- невидимое ребро,
на втором – EK, LK и KF.
Решим несколько типовых задач на тетраэдр:
Найти площадь развертки правильного тетраэдра с ребром 5 см.
Решение. Начертим развертку тетраэдра
(на экране появляется развертка тетраэдра )
Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.
Площадь правильного треугольника ищем по формуле:
Тогда получаем площадь тетраэдра равна:
Подставим в формулу длину ребра а=5 см,
Ответ: Площадь развертки правильного тетраэдра
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.
а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.
б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.
—> —>
| Инфоурок |
| 28.10.2014 |
| Геометрия |
| Видеоурок |
| 3844 |
| 926 |
© 2019 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тетраэдр и его элементы
Как построить тетраэдр? Возьмем произвольный треугольник АВС. Произвольную точку D, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.
Рис. 1. Тетраэдр АВСD
Замечание: можно принять плоскость АВС за основание тетраэдра, и тогда точка D является вершиной тетраэдра. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ – это пересечение плоскостей АВD и АВС. Каждая вершина тетраэдра – это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС, АВD, АDС. Точка А – это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВD ∩ АСD.
Тетраэдр определение
Итак, тетраэдр — это поверхность, образованная четырмя треугольниками.
Ребро тетраэдра — линия перечесения двух плоскостей тетраэдра.
Задача 1 на построение тетраэдра
Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.
На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.
Задача 2 Построить сечение тетраэдра плоскостью
Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит ребру тетраэдра ВD и точка Р принадлежит ребру DС (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP.
Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим грань тетраэдра DВС. В этой грани точки  Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е (Рис. 3.).
Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е (Рис. 3.).
Рис. 3. Рисунок к задаче 2. Нахождение точки Е
Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях — АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.
Итак, в этом случае NPQМ — искомое сечение.
Рис. 4. Рисунок к задаче 2.Решение задачи 2
Рассмотрим теперь случай, когда NP параллельна BC. Если прямая NP параллельна какой-нибудь прямой, например, прямой ВС из плоскости АВС, то прямая NP параллельна всей плоскости АВС.
Искомая плоскость сечения проходит через прямую NP, параллельную плоскости АВС, и пересекает плоскость по прямой МQ. Значит, линия пересечения МQ параллельна прямой NP. Получаем, NPQМ — искомое сечение.
Задача 3 Построить сечение тетраэдра плоскостью
Точка М лежит на боковой грани АDВ тетраэдра АВСD. Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС.
Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью
Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ, АС, ВС.
В плоскости АВD через точку М проведем прямую PQ параллельно АВ (рис. 5). Прямая PQ лежит в плоскости АВD. Аналогично в плоскости АСD через точку Р проведем прямую РR параллельно АС. Получили точку R. Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС, значит, плоскости АВС и РQR параллельны. РQR – искомое сечение. Задача решена.
Задача 4
Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС (Рис. 6.). Построить точку пересечения прямой NM и плоскости АВС.
Рис. 6. Рисунок к задаче 4
Решение:
Для решения построим вспомогательную плоскость DМN.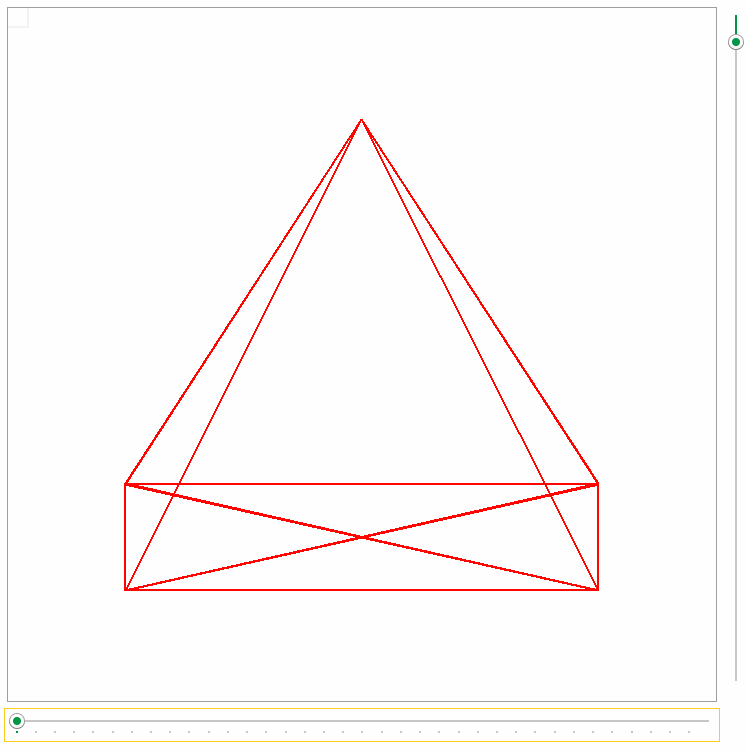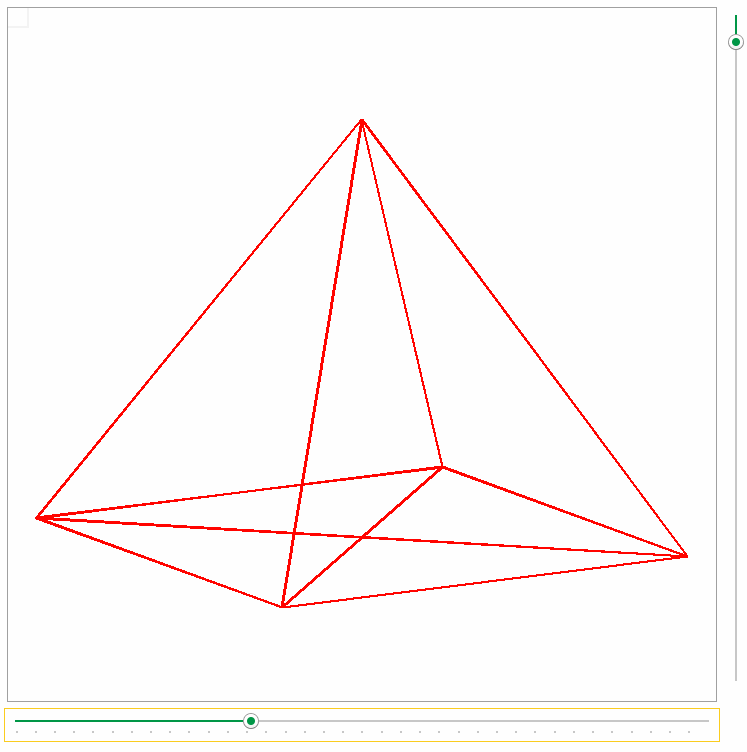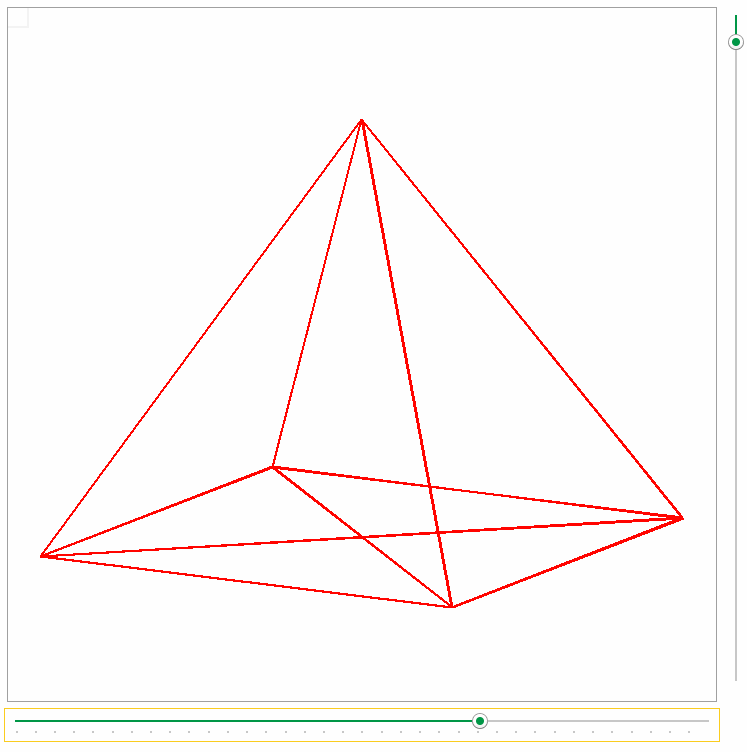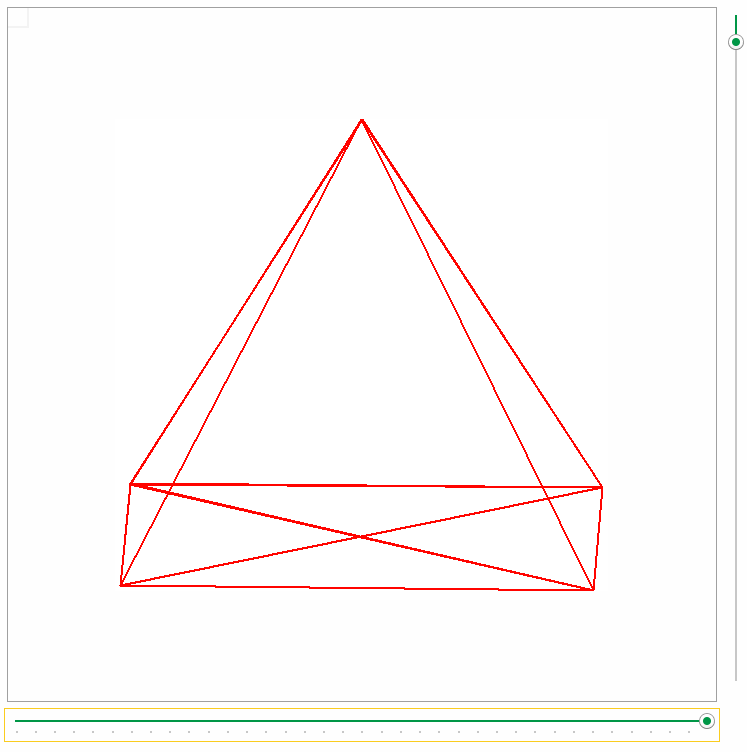 Пусть прямая DМ пересекает прямую АВ в точке К (Рис. 7.). Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.
Пусть прямая DМ пересекает прямую АВ в точке К (Рис. 7.). Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.
Рис. 7. Рисунок к задаче 4. Решение задачи 4
Задача 5 Построить сечение тетраэдра плоскостью
Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС (Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.
Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС. В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.
В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.
Рис. 9. Рисунок к задаче 5. Нахождение точки К
Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС. Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2параллельна данной прямой MN (Рис.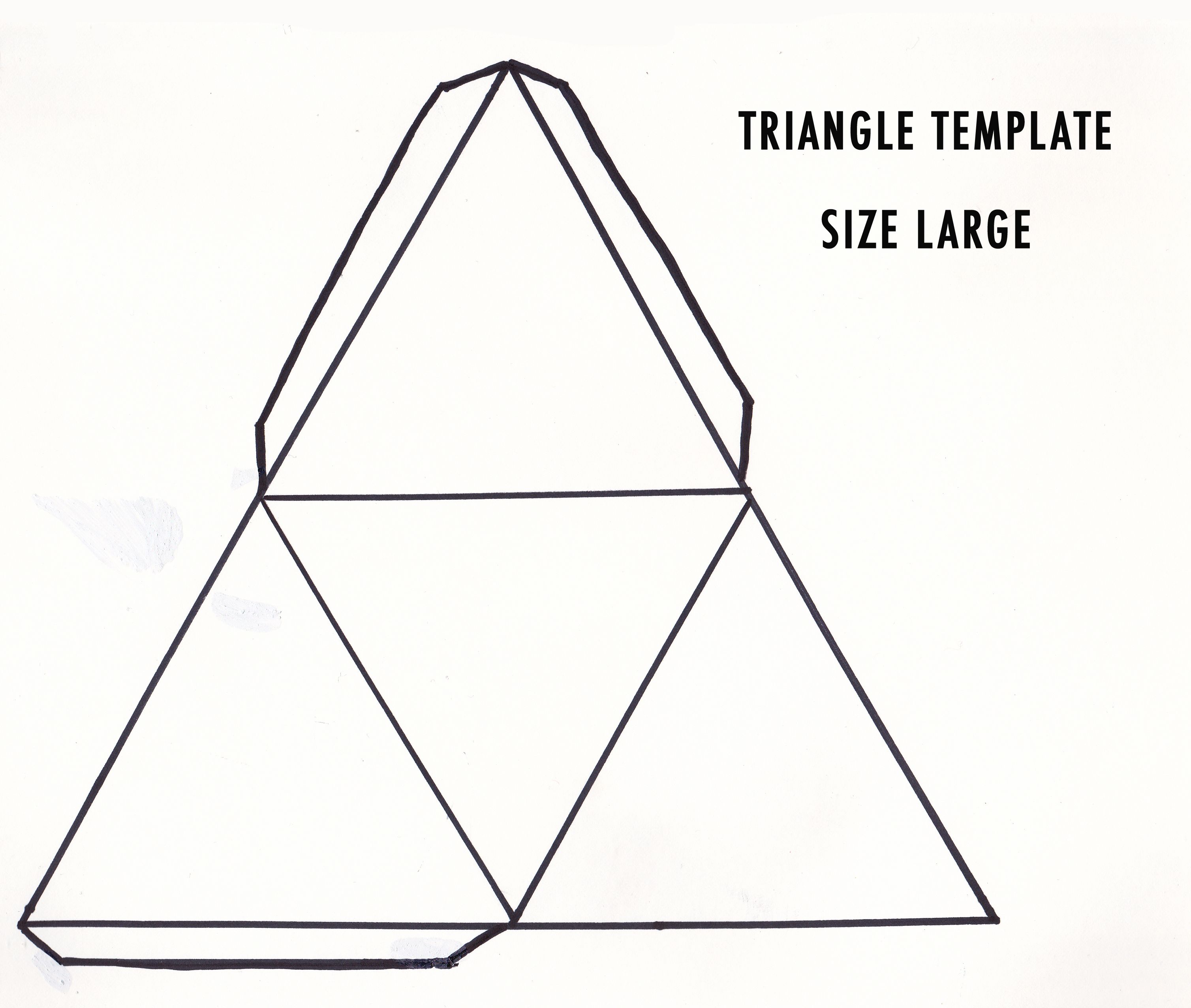 10.).
10.).
Рис. 10. Рисунок к задаче 5. Искомое сечение
Итоги урока по теме «Тетраэдр», «Ребро тетраэдра», «Грани тетраэдра», «Поверхность тетраэдра», «Вершины тетраэдра»
Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.
Список рекомендованной литературы по теме «Тетраэдр»
1. И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни)
2. Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений
3. Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики
Дополнительные веб-ресурсы
1. Сечения тетраэдра (Источник).
Сечения тетраэдра (Источник).
2. Как построить сечение тетраэдра. Математика (Источник).
3. Фестиваль педагогических идей (Источник).
Сделай дома задачи по теме «Тетраэдр», как находить ребро тетраэдра, грани тетраэдра, вершины и поверхность тетраэдра
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил. Задания 18, 19, 20 стр. 50
2. Точка Е середина ребра МА тетраэдра МАВС. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и Е.
3. В тетраэдре МАВС точка М принадлежит грани АМВ, точка Р – грани ВМС, точка К – ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точки М, Р, К.
4. Какие фигуры могут получиться в результате пересечения плоскостью тетраэдра?
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
«>
как нарисовать тетраэдр — 8 рекомендаций на Babyblog.ru
http://www.elitarium.ru/2012/03/30/razvitie_obraznogo_myshlenija.htmlНаглядно-образное мышление и воображение — это разные процессы. Наглядно-образное имеет дело с реальным предметом, процессом. Воображение же — это воссоздание нужного образа из образной памяти. Вы можете привлечь свое воображение для избавления от стресса, обретения эмоционального равновесия, получения позитивного настроя, успешного взаимодействия с деловым и личным окружением. Предлагаем несколько упражнений для развития образного мышления.
Автор: Eкaтepина Евгeньевна Bacильeвa, доктор педагогических наук, профессор Российской академии естественных наук.
Наглядно-образное мышление — это совокупность способов и процессов образного решения задач, предполагающих зрительное представление ситуации и оперирование образами составляющих ее предметов, без выполнения реальных практических действий с ними. Такое мышление позволяет наиболее полно воссоздавать все многообразие различных фактических характеристик предмета. Важной особенностью этого вида мышления является установление непривычных сочетаний предметов и их свойств. В этом своем качестве наглядно-образное мышление неразличимо с воображением.
Важной особенностью этого вида мышления является установление непривычных сочетаний предметов и их свойств. В этом своем качестве наглядно-образное мышление неразличимо с воображением.
Наглядно-образное мышление и воображение — разные процессы. Наглядно-образное имеет дело с реальным предметом, процессом. Воображение же — это воссоздание нужного образа из образной памяти.
Как у вас обстоят дела с образным мышлением? Посмотрите на ладонь вашей левой руки. Тщательно изучите ее. Обратите внимание на линии, трещинки и родинки, на узоры на коже. Полюбуйтесь, как игра света и тени образует неуловимые перемены в цвете. Примерно через минуту, когда вы будете иметь ясное представление о том, как выглядит ваша ладонь, закройте глаза и постарайтесь воспроизвести ее вид в уме, создайте четкий мысленный образ ладони.
Через некоторое время откройте глаза, посмотрите на ладонь и сравните ее с картиной, которую вы нарисовали в воображении. Отметьте, что присутствовало, а что отсутствовало в созданном вами образе.
Затем закройте глаза и вновь представьте вашу ладонь. Вообразите, как она выглядела бы, если бы вы смотрели на нее открытыми глазами. Еще через полминуты откройте глаза и посмотрите на ладонь. Повторите весь цикл не менее шести раз. С каждым разом старайтесь добавлять еще больше ясности созданному вами образу.
Если образ будет не таким ясным, как хотелось бы, не заставляйте его стать четче силой воли, лучше попробуйте без напряжения пройтись по признакам, визуализируя последовательно форму, текстуру, размер, цвет.
Чтобы усилить яркость мысленного «изображения», надо отключить вербальное (словесное) мышление, просто смотреть, но не описывать его словами.
Вы можете привлечь свое воображение для избавления от стресса, обретения эмоционального равновесия, получения позитивного настроя, успешного взаимодействия с деловым и личным окружением — лучше его чувствуя и находя взаимопонимание. Предлагаем вам далее несколько упражнений для развития образного мышления.
1. Мысленный образ праздничного ужина
Мысленный образ праздничного ужина
Минуту или две мысленно нарисуйте картину последнего праздничного ужина, на котором вы присутствовали: представьте людей, с которыми вы были, окружающую обстановку, убранство стола, вкус пищи, слова и звуки, которые до вас доносились. Итак, прежде чем продолжить чтение, прервитесь на некоторое время и попробуйте создать образ, стараясь не упустить из виду детали. Начинайте прямо сейчас.
Затем ответьте на следующие вопросы:
- Созданный вами образ получился четким или расплывчатым?
- Скажите, картина получилась более тусклой, чем реальная сцена, или нет?
- Детали выбранной вами конкретной сцены видны отчетливо все как одна или же некоторые из них выделяются больше, чем другие?
- Возникающая в вашем воображении картина цветная или просто сероватых оттенков?
- Если картина цветная, точны ли цветовые оттенки?
- Можете ли вы создать цельный зрительный образ всего помещения?
- Можете ли вы сохранить в воображении устойчивый образ вашей тарелки? Если это реально, скажите, становится ли он четче по истечении времени?
- Можете ли вы мысленно увидеть вашу тарелку, ваши руки, держащие нож и вилку, лицо сидящего напротив человека — и все это в одно и то же время?
- Можете ли вы почувствовать вкус блюд, которые вы ели?
- Можете ли вы обрисовать, как были одеты люди?
2. Реальный предмет
Реальный предмет
Представьте каждый из перечисленных далее предметов:
- лицо человека;
- друг детства;
- бегущая собака;
- ваша спальня;
- закат;
- летящий орел;
- журчащий ручей;
- капля росы;
- перистые облака;
- клавиатура компьютера;
- дубрава;
- снежная вершина;
- зубная щетка;
- ваша любимая пара обуви.
Если возникающие образы не так ярки, как вам бы хотелось, не пытайтесь насильно улучшить их. Вместо этого сосредоточьтесь на самой идее созерцания образа. Помните: все, что вы пытаетесь представить, имеет форму, качество, цвет и размер. Сфокусируйтесь сначала на форме, а затем погрузитесь в детали. Дайте время образу стать устойчивым и резким.
3. Не очень реальный предмет
Какая разница между образами предметов, которые вы видели, и образами предметов, которые вы никогда не видели? Нарисуйте в уме следующие картины:
- единорог;
- шоколадная река;
- шестирукий бог;
- говорящий жираф;
- тридцатиногий муравей;
- хор ангелов;
- четырехмерная сфера;
- хоббит;
- пятилистный клевер.

4. Квадраты бокового зрения
Сохраняя взгляд неподвижным, постарайтесь обозреть периферию вашего поля зрения. Используйте боковое зрение,чтобы увидеть как можно больше. Затем закройте глаза и попробуйте воссоздать образ увиденного. Мысленно разбейте обозреваемое пространство на четыре части. Выберите квадрат и проанализируйте каждую деталь в этом квадрате, потом мысленно воссоздайте его. Повторите это с каждым квадратом.
5. Пять мысленных картин
- Представьте себе пять голубых предметов (голубика, небо, обложка книги…).
- Проделайте то же самое с другими красками: красной, желтой, зеленой, пурпурной…
- Отчетливо представьте себе пять предметов, начинающихся с буквы «А» (артишок, амфора…).
- Проделайте то же самое с каждой буквой алфавита.
- Представьте пять предметов меньше вашего мизинца (колпачок ручки, горошина, нервная клетка…).
- Представьте пять предметов больше автобуса (кит, поезд…).
- Представьте себе пять предметов, находящихся под землей (корни, дождевые черви.
 ..).
..). - Представьте пять вещей, доставляющих вам радость (катание на лыжах, плавание в море, мороженое, прогулка по лесу…).
6. Зрительный след
Если, посмотрев на некий объект, вы закроете глаза, то его образ автоматически сохранится в вашей памяти еще на какое-то время. Постарайтесь соединить зрительную память с вашим мысленным представлением. Например, посмотрите на ручку, закройте глаза и полюбуйтесь картиной, сохраненной в памяти. Когда образ потускнеет, откройте глаза, посмотрите на ручку, снова закройте глаза и снова посмотрите на ее образ в вашей памяти. Повторите это несколько раз в удобном для вас темпе, пока у вас хотя бы на секунду не вырисуется четкая картина. После этого постарайтесь уже сознательно воспроизвести мысленный образ ручки.
7. Периферическое мысленное зрение
Мысленно представьте ручку, расположенную прямо перед вами. Затем также мысленно начинайте медленно перемещать ее в пространстве — так, чтобы она вначале была слева от вас, затем за вами, затем справа от вас и, наконец, опять перед вами. Одновременно с передвижением ручки воображайте, что вы используете периферическое зрение, чтобы следить за ней.
Одновременно с передвижением ручки воображайте, что вы используете периферическое зрение, чтобы следить за ней.
8. Мысленные портреты
Вспомните всех людей, с которыми вы сегодня разговаривали. Как они выглядели? Какого цвета у них волосы и глаза? Какого они роста и возраста? Во что они были одеты? Можете ли вы представить их манеры и привычки? Нарисуйте портреты людей, которых вы видели вчера; в прошлые выходные; во время последнего отпуска; на последнем дне рождения.
9. Геометрические тела
Большая часть математических операций выполняется с воображаемыми объектами. Представьте каждое из перечисленных далее трехмерных тел:
- сфера;
- куб;
- призма;
- тетраэдр;
- пирамида;
- додекаэдр;
- октаэдр;
- икосаэдр.
Не старайтесь сразу же создать образ: вначале подробно изучите пространственное взаиморасположение плоских граней. Мысленно манипулируйте телами, рассматривая их со всех сторон, в том числе и изнутри. Постарайтесь получить ощущение объемности тела.
Постарайтесь получить ощущение объемности тела.
10. Чувства и ничего, кроме чувств
Вообразите положительную эмоцию. Представьте чувство изумления, не имея при этом в виду никакого конкретного объекта или воспоминания. Попытайтесь представить желание, ничего конкретно не желая. Насколько наглядно вы можете мысленно воспроизвести следующие переживания: надежду, радость, удовольствие, любовь, гнев, апатию?
11. Настройка телевизора
Выберите какой-нибудь определенный объект, например ватрушку с черникой, и постарайтесь мысленно создать ее четкий образ. Вообразите, что можете регулировать качество внутреннего изображения — так же, как, нажимая на кнопки, вы настраиваете телевизор.
Сначала сформируйте устойчивый образ ватрушки и увеличьте резкость. Можете ли вы различить крошки? Можете ли вы разглядеть оттенок ягод? Можете ли вы определить цвет теста? Затем поверните регулятор резкости так, чтобы изображение получилось расплывчатым и неясным. Затем снова поверните ручку в обратном направлении, чтобы изображение стало четким — насколько это возможно. Сколько деталей вы можете рассмотреть в крошках ватрушки? Является ли возникающий образ объемным? Далее вновь поверните регулятор резкости в противоположную сторону и сделайте изображение опять расплывчатым. Попеременно формируйте то четкую, то расплывчатую картину, пока эта смена не станет для вас технически элементарно выполнимой. Таким же образом постарайтесь отрегулировать и другие переключатели.
Сколько деталей вы можете рассмотреть в крошках ватрушки? Является ли возникающий образ объемным? Далее вновь поверните регулятор резкости в противоположную сторону и сделайте изображение опять расплывчатым. Попеременно формируйте то четкую, то расплывчатую картину, пока эта смена не станет для вас технически элементарно выполнимой. Таким же образом постарайтесь отрегулировать и другие переключатели.
12. Образы идей
Вообразите себе идею Красоты. Скажите, вы видите определенный образ чего-то очень красивого или способны создать абстрактный образ Красоты, не представляя себе ничего конкретного, частного? Связываете ли вы с вашей идеей Красоты звуки, запахи, вкусовые ощущения? Насколько велика или мала эта идея? Приведем еще несколько абстрактных понятий, образ которых вам предлагается создать: измена, порядок, энергия, мир, гармония, общение, реальность, иллюзия.
Какие творческие навыки самоменеджмента и личной эффективности вы хотели бы приобрести до начала лета? При обучении по индивидуальной программе сроком на 6 мес.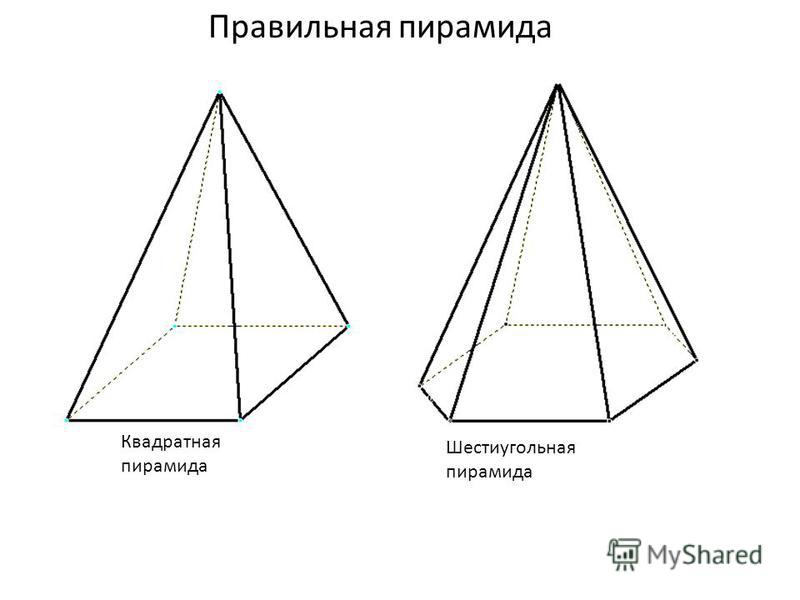 или 1 год (в зависимости от того, сколько курсов вы хотите изучить) опытный куратор поможет вам составить свой системный план обучения издесятков практических дисциплин. Тем самым вы получаете системную учебную программу, которая включает в себя только те практические знания и навыки, которые вам интересны и нужны.
или 1 год (в зависимости от того, сколько курсов вы хотите изучить) опытный куратор поможет вам составить свой системный план обучения издесятков практических дисциплин. Тем самым вы получаете системную учебную программу, которая включает в себя только те практические знания и навыки, которые вам интересны и нужны.
Развертка тетраэдра, схема, шаблон и развертка тетраэдра из бумаги, как сделать тетраэдр самому из картона
Дата публикации: .
Из истории
Тетраэдр еще одна удивительная фигура, которая довольно часто встречается в нашей жизни, но обычно наши знания о нем ограничиваются определением, свойствами и формулами из школьного курса геометрии.
Слово «тетраэдр» образовано из двух греческих слов: tetra – переводиться как четыре и hedra – означает основание, грань; в каждой вершине тетраэдра сходятся по 3 грани. Эта фигура имеет 4 грани, 6 ребер и 4 вершины.
С самых древних времен представления людей о красоте были связаны с симметрией. Возможно, этим объясняется интерес людей к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей и людей всех эпох. Уже во времена Пифагора дивились их красоте и симметрии. Ученики Пифагора считали, что правильные многогранники – это божественные фигуры и использовали их в философских сочинениях. Первоосновам бытия – огню, воздуху, воде, земле придавалась форма соответственно октаэдра, икосаэдра, тетраэдра, куба, а Вселенная представлялась в форме додекаэдра. Ученики Платона продолжили изучение перечисленных тел, поэтому эти многогранники называют Платоновыми телами.
Возможно, этим объясняется интерес людей к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей и людей всех эпох. Уже во времена Пифагора дивились их красоте и симметрии. Ученики Пифагора считали, что правильные многогранники – это божественные фигуры и использовали их в философских сочинениях. Первоосновам бытия – огню, воздуху, воде, земле придавалась форма соответственно октаэдра, икосаэдра, тетраэдра, куба, а Вселенная представлялась в форме додекаэдра. Ученики Платона продолжили изучение перечисленных тел, поэтому эти многогранники называют Платоновыми телами.
Роль задач о тетраэдрах очень высока в развитии математического мышления школьников. Эти задачи стимулируют накопление геометрических представлений и знаний, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.
Где можно встретить тетраэдр? Тетраэдр, такая удивительная геометрическая фигура, которая встречается нам повсюду, но с первого взгляда ее не так просто заметить. Тетраэдр может образовать жёсткую конструкцию. Выполненный из стержней, его часто используют в качестве основы для пространственных конструкций балок, ферм мостов, пролётов зданий, перекрытий и т. д. Прямоугольный тетраэдр давно используется в оптике. На велосипедах отражатели катафоты имеют форму тетраэдра. Благодаря свойствам тетраэдра, катафоты отражают свет и другим людям и водителям видно велосипедиста. Если внимательно присмотреться, то внутри катафота видно множество форм тетраэдра.
Тетраэдр может образовать жёсткую конструкцию. Выполненный из стержней, его часто используют в качестве основы для пространственных конструкций балок, ферм мостов, пролётов зданий, перекрытий и т. д. Прямоугольный тетраэдр давно используется в оптике. На велосипедах отражатели катафоты имеют форму тетраэдра. Благодаря свойствам тетраэдра, катафоты отражают свет и другим людям и водителям видно велосипедиста. Если внимательно присмотреться, то внутри катафота видно множество форм тетраэдра.
Виды тетраэдра
Фигуру тетраэдр можно разделить на несколько видов, какие они бывают?
Равногранный тетраэдр, все его грани являются равными между собой треугольниками;
Ортоцентрический тетраэдр, высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке;
Прямоугольный тетраэдр, ребра, прилежащие к одной из вершин, являются перпендикулярными между собой;
Правильный тетраэдр, это тетраэдр, грани которого являются равносторонними треугольниками,
Инцентрический тетраэдр, его отрезки соединяют вершины с центрами окружностей, которые вписаны в противоположные грани и пересекаются в одной точке.
Выделяют так же каркасный тетраэдр, соразмерный тетраэдр.
Тетраэдр – подсказанное нам природой идеальное равновесие, в основе которого, идеальность равнобедренного треугольника. Тетраэдр – треугольник, но только в объемном виде, в наше время его можно назвать 3D треугольник.
Пополнить свою коллекцию геометрических фигур новой фигурой – тетраэдром, вы можете используя развертки, представленные на нашем сайте. Тетраэдр, собранный по этим разверткам можно использовать для обучения, например, что бы научить детишек считать, узнавать цвета, можно объяснить, что такое плоскость и объем, что такое треугольник др.
Развертка тетраэдра из бумаги или из картона
| Схема тетраэдра с арабскими цифрами 1,2,3,4 (грань 10 см) | Схема тетраэдра с арабскими цифрами 5,6,7,8 (грань 10 см) | Схема тетраэдра с арабскими цифрами 0,1,2,9 (грань 10 см) |
| JPG | JPG | JPG |
| Схема разноцветного тетраэдра №1 (грань 10 см) | Схема разноцветного тетраэдра №2 (грань 10 см) | Схема разноцветного тетраэдра №3 (грань 10 см) |
| JPG | JPG | JPG |
| Схема простого тетраэдра (грань — 10 см) | Схема тетраэдра с формулами (грань 10 см) | Схема тетраэдра с героями советских мультиков (грань — 10 см) |
| JPG | JPG | JPG |
| Тетраэдр-календарь на 2013 год (январь-апрель, грань 10 см) | Тетраэдр-календарь на 2013 год (май-август, грань 10 см) | Тетраэдр-календарь на 2013 год (сентябрь-декабрь, грань 10 см) |
| JPG | JPG | JPG |
Григорий Андреев
%d1%82%d0%b5%d1%82%d1%80%d0%b0%d1%8d%d0%b4%d1%80 перевод на чешский
Когда в 80-х годах люди якудзы увидели, как легко брать ссуды и «делать» деньги, они создали компании и занялись операциями с недвижимым имуществом и куплей-продажей акций.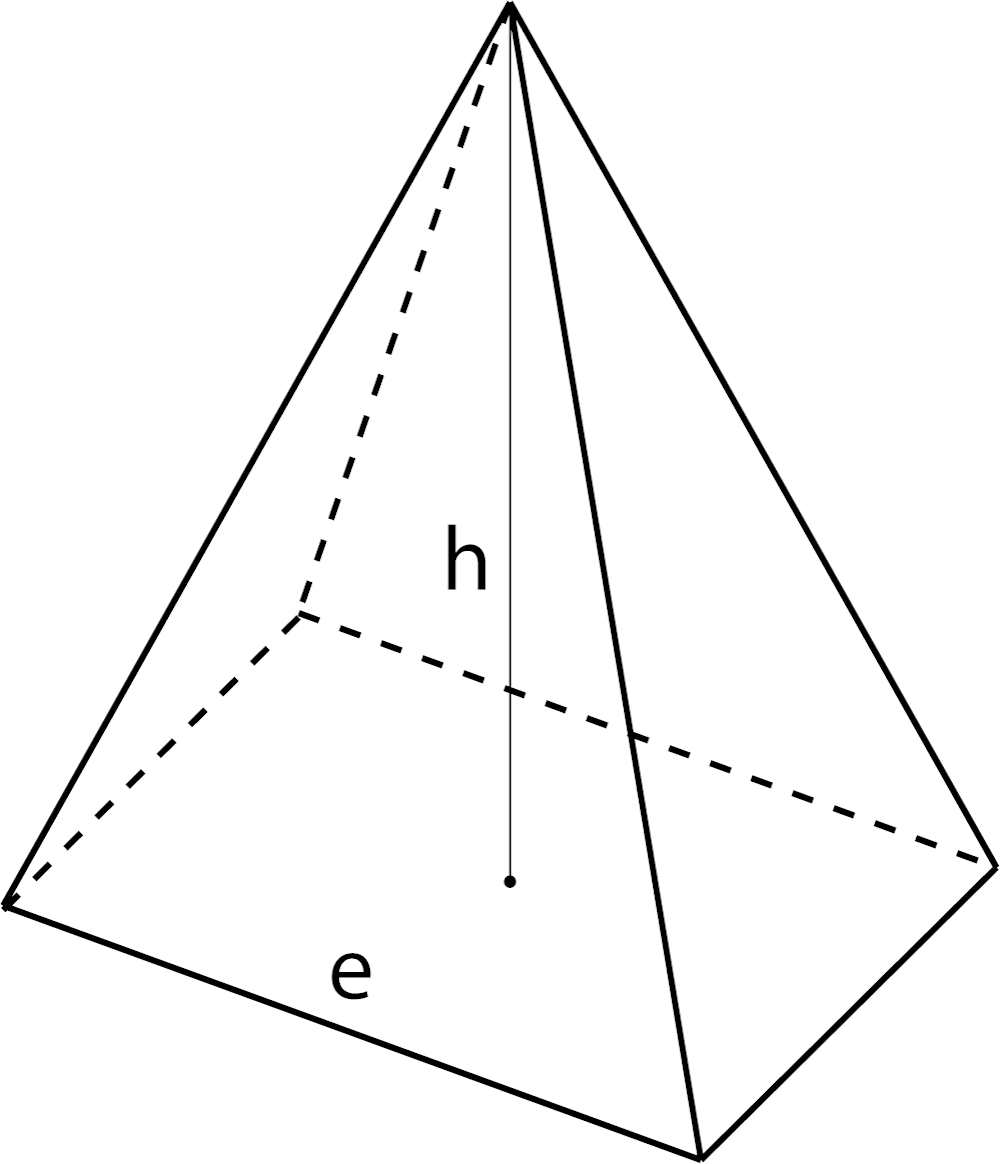
Když v osmdesátých letech jakuza viděla, jak snadné je půjčovat si a vydělávat peníze, vytvořila společnosti a vrhla se na obchod s nemovitostmi a na spekulace na burze.
jw2019
Обычно проводят связь между этим древним городом и современной Газой (Газза, Азза), расположенной примерно в 80 км к З.-Ю.-З. от Иерусалима.
Obvykle je starověké město spojováno s dnešní Gazou (Ghazze; ʽAzzou), která leží asi 80 km na ZJZ od Jeruzaléma.
jw2019
С 2002 по 2010 годы из $56 млрд финансовой помощи, предоставленной Афганистану, 82% было потрачено через негосударственные институты.
Mezi lety 2002 a 2010 bylo 82% z 56 miliard dolarů určených na pomoc v Afghánistánu utraceno prostřednictvím nestátních institucí.
ProjectSyndicate
Через 4 года предполагаемая капитализация достигнет 80 миллиардов долларов.
Během čtyř let se odhaduje, že bude mít cenu osmdesáti.
ted2019
Этот эффективный альтруист подсчитал, что на деньги, которые он предположительно сможет заработать за свою карьеру в качестве научного сотрудника, можно было бы вылечить 80 000 слепых людей в развивающихся странах, и при этом у него останется достаточно средств для поддержания достойного уровня жизни.
Stal se efektivním altruistou, když spočítal, že s penězi, které si pravděpodobně vydělá za svou kariéru, akademickou kariéru, by byl schopen darovat dostatek na to, aby bylo 80. 000 lidí vyléčeno ze slepoty v rozvojových zemích a že mu stále zůstane dost na zachování adekvátního životního standardu.
QED
В «Атласе языков мира, находящихся под угрозой исчезновения» (Atlas of the World’s Languages in Danger) организации UNESCO приводятся оценочные данные по численности носителей диалектов тазнатит на 2008 год в 80 000 человек.
Dnes je votština zařazena v Atlasu ohrožených jazyků UNESCO a počet jejich mluvčích je k roku 2008 odhadován na 20 lidí.
WikiMatrix
Сегодня он фонтанирует в среднем через каждые 80 минут.
V dnešní době je průměrný interval asi 80 minut.
jw2019
Мы отвечали за территорию, которая простиралась от демилитаризованной зоны между Северным и Южным Вьетнамом до Дананга и еще 80 километров на юг.
Starali jsme se o území od demilitarizované zóny mezi Severním a Jižním Vietnamem až po oblast asi 80 km od Danangu.
jw2019
82 помещается в 500 — Хорошо, давайте посмотрим.
Dobře podívejme se na to.
QED
Этот отчисленный ученик умер в 82 года, в здравом уме, будучи основателем и первым директором Еврейского университета в Иерусалиме и основателем издательства Шокен Букс. Это популярное издательство в дальнейшем было поглощено издательским домом Рандом Хаус.
Tento středoškolský odpadlík zemřel ve věku 82 let jako respekt vzbuzující intelektuál, spoluzakladatel a první CEO Hebrejské univerzity v Jeruzalému, zakladatel Schocken Books, uznávaného nakladatelství, které později koupil Random House.
ted2019
Мы облетим эти два пульсара на минимальном расстоянии в 80 миллионов километров.
Budeme obíhat ty dva pulsary ve vzdálenosti alespoň 80 milionů kilometrů.
OpenSubtitles2018.v3
Девочки, мне уже почти 80.
OpenSubtitles2018.v3
И потому что оставшиеся 80% были все-равно раз в сто больше того, что вы получили бы при разводе.
A protože zbývajících 80% bylo stále asi tak stokrát víc, než byste dostala z rozvodu.
OpenSubtitles2018.v3
82-летний мужчина, диабетик, похищен около своего маленького милого дома среди бела дня.
Dvaaosmdesátiletý muž, diabetik, unesen za bílého dne, ze zahrady svého pěkného domečku.
OpenSubtitles2018.v3
▪ Ежедневно в ЮАР осуждаются 82 ребенка за «изнасилование или словесное оскорбление других детей».
▪ V Jižní Africe je každý den před soudem obviněno 82 dětí ze „znásilnění nebo sexuálního obtěžování jiných dětí“.
jw2019
И типа, IQ у этого парня был сколько, 80?
A ten chlap měl IQ tak 80 nebo kolik, že?
OpenSubtitles2018.v3
Среднемесячная же заработная плата в этом районе составляет лишь около 80 долларов!
V této oblasti je měsíční výdělek v průměru kolem osmdesáti dolarů!
jw2019
Мы говорим здесь о волне высотой в 80 метров.
Bavíme se tady o vlně vysoké 80 metrů.
OpenSubtitles2018.v3
Это шоу слишком прекрасно для 80 мест.
To představení je až moc dobré pro 80 sedadel.
OpenSubtitles2018.v3
В 1999 году население села составляло 150 человек (80 мужчин и 70 женщин).
Osadu bránilo 150 jejích obyvatel (80 mužů a 70 žen).
WikiMatrix
Нам нужно трудиться вместе с 80 тысячами ныне призванных миссионеров.
Je třeba, abychom spolupracovali v partnerství s 80 000 misionáři, kteří nyní slouží na misii.
LDS
Однако торонтская газета «Глоб энд мейл» замечает: «В 80 процентах случаев одна или больше групп общества (включая друзей или сотрудников преступника по работе, семьи жертв, других детей, а также некоторых жертв) отрицали или приуменьшали случившееся».
Torontský The Globe and Mail si však všímá: „V osmdesáti procentech případů jedna nebo více složek společnosti (včetně přátel nebo spolupracovníků úchylného člověka, rodin obětí, jiných dětí i včetně některých obětí) zneužití popíraly nebo zlehčovaly.“
jw2019
Во всем мире Свидетели Иеговы стали „сильным народом“. Их объединенное всемирное собрание по численности превосходит население не менее 80 отдельно взятых государств мира».
Na celém světě se stali svědkové Jehovovi ‚mocným národem‘ — jako sjednocený celosvětový sbor jsou národem početně větším než nejméně 80 jednotlivých samostatných států světa.“
jw2019
В газете «Репубблика» утверждалось, что в неделю опроса 82 процента итальянцев смотрели телевизор, «и они просиживали у экранов в среднем чуть меньше пяти часов» в день.
Noviny La Repubblica uvádějí, že během jednoho týdne, který byl ve studii hodnocen, se na televizi dívalo 82 procent Italů, „a ti strávili před televizí téměř pět hodin“ denně.
jw2019
В среднем, соотношение государственного долга и ВВП в Кита составляет около 20%, в то время как в США эта цифра превышает 80%, составляя 160% для Японии и 60-90% для Европы.
Ostatně poměr státního zadlužení k HDP činí asi 20%, oproti více než 80% ve Spojených státech, 160% v Japonsku a 60-90% v Evropě.
News commentary
Рисунки для Тины всегда отличаются сакральным смыслом и глубиной😍🤗 Сегодня рисовали Меркабу🌞 Этот символ предназначен для исцеления и баланса, будучи одним из самых мощных символов.
 Меркаба также способствует духовному росту и соединению с высшим Я
🪶
По своей сути, Меркаба – это мощное энергетическое Поле Света, окружающее физическое тело человека.
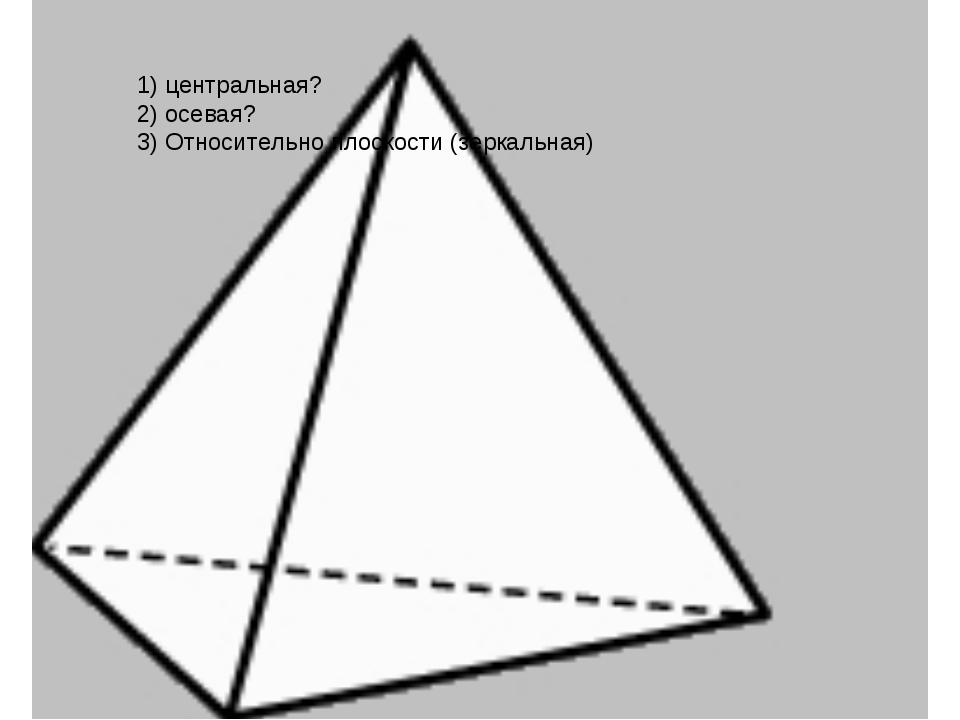
По одной версии, тетраэдр направленный вверх — это солнечный тетраэдр, а направленный вниз — земной тетраэдр (еще вариант, что направленный вниз тетраэдр именуют лунным). По другой версии, тетраэдр направленный вверх — это мужской тетраэдр, а направленный вниз
❤
Запись на мехенди по тел/вайберу 067 4658732 #СветланаЗиновьева
#мехендикиев
#mehndi #hennaart #красивоемехенди
#красивоемехендикиев #мехендируки
#мехендигрудь
#мехендиспина
#мехендипоясница
#росписьхнойкиев
#татухнойкиев
#биотатукиев #мастермехендикиев #обучениемехендикиев #школамехенди #мехендитату #мехендивпотоке #мехендимедитация #мехендирелакс…Рисунки для Тины всегда отличаются сакральным смыслом и глубиной😍🤗
Сегодня рисовали Меркабу🌞 Этот символ предназначен для исцеления и баланса, будучи одним из самых мощных символов. Меркаба также способствует духовному росту и соединению с высшим Я
🪶
По своей сути, Меркаба – это мощное энергетическое Поле Света, окружающее физическое тело человека.
Меркаба также способствует духовному росту и соединению с высшим Я
🪶
По своей сути, Меркаба – это мощное энергетическое Поле Света, окружающее физическое тело человека.
По одной версии, тетраэдр направленный вверх — это солнечный тетраэдр, а направленный вниз — земной тетраэдр (еще вариант, что направленный вниз тетраэдр именуют лунным). По другой версии, тетраэдр направленный вверх — это мужской тетраэдр, а направленный вниз
❤
Запись на мехенди по тел/вайберу 067 4658732 #СветланаЗиновьева
#мехендикиев
#mehndi #hennaart #красивоемехенди
#красивоемехендикиев #мехендируки
#мехендигрудь
#мехендиспина
#мехендипоясница
#росписьхнойкиев
#татухнойкиев
#биотатукиев #мастермехендикиев #обучениемехендикиев #школамехенди #мехендитату #мехендивпотоке #мехендимедитация #мехендирелакс…Рисунки для Тины всегда отличаются сакральным смыслом и глубиной😍🤗
Сегодня рисовали Меркабу🌞 Этот символ предназначен для исцеления и баланса, будучи одним из самых мощных символов. Меркаба также способствует духовному росту и соединению с высшим Я
🪶
По своей сути, Меркаба – это мощное энергетическое Поле Света, окружающее физическое тело человека.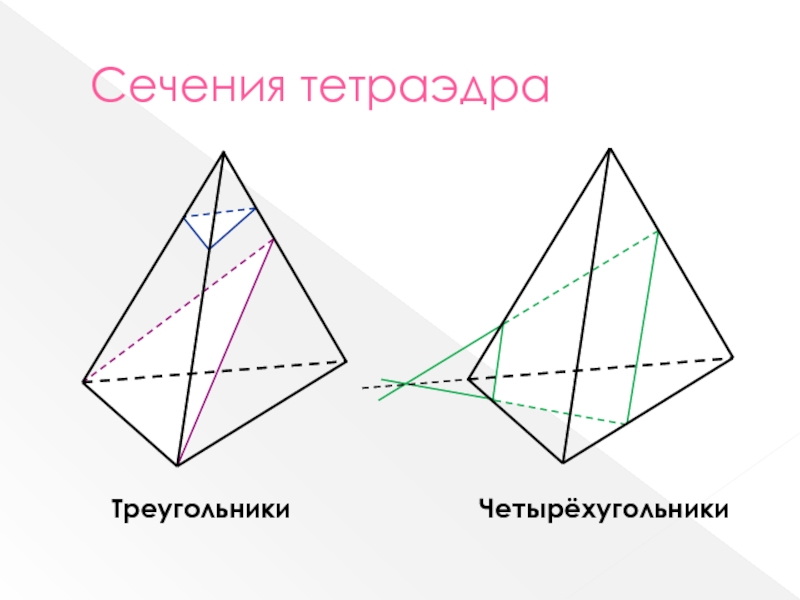 По одной версии, тетраэдр направленный вверх — это солнечный тетраэдр, а направленный вниз — земной тетраэдр (еще вариант, что направленный вниз тетраэдр именуют лунным). По другой версии, тетраэдр направленный вверх — это мужской тетраэдр, а направленный вниз — женский тетраэдр. Одна из духовных школ дает следующее описание: «Меркаба человека представляет собой взаимодействие между собой трёх тел: физического, астрального и ментального. Тетраэдр направленный вверх должен вращаться по часовой стрелке, тетраэдр направленный вниз должен вращаться против часовой стрелки. При определённой скорости вращения тонких тел называемой критической, поле вокруг человека превращается в кристалл, который и называется активированной меркабой. Если в этом состоянии у человека активированы сверх способности и он владеет знаниями тонких планов, то с помощью своей меркабы он способен творить чудеса — перемещаться сквозь пространство, летать в воздухе, переходить в параллельные миры, летать на другие планеты в тонких телах и пр.
По одной версии, тетраэдр направленный вверх — это солнечный тетраэдр, а направленный вниз — земной тетраэдр (еще вариант, что направленный вниз тетраэдр именуют лунным). По другой версии, тетраэдр направленный вверх — это мужской тетраэдр, а направленный вниз — женский тетраэдр. Одна из духовных школ дает следующее описание: «Меркаба человека представляет собой взаимодействие между собой трёх тел: физического, астрального и ментального. Тетраэдр направленный вверх должен вращаться по часовой стрелке, тетраэдр направленный вниз должен вращаться против часовой стрелки. При определённой скорости вращения тонких тел называемой критической, поле вокруг человека превращается в кристалл, который и называется активированной меркабой. Если в этом состоянии у человека активированы сверх способности и он владеет знаниями тонких планов, то с помощью своей меркабы он способен творить чудеса — перемещаться сквозь пространство, летать в воздухе, переходить в параллельные миры, летать на другие планеты в тонких телах и пр. » Сложно, но очень интересно😁
❤
Запись на мехенди по тел/вайберу 067 4658732 #СветланаЗиновьева
#мехендикиев
#mehndi #hennaart
#красивоемехенди
#красивоемехендикиев
#мехендируки
#мехендигрудь
#мехендиспина
#мехендипоясница
#росписьхнойкиев
#татухнойкиев
#биотатукиев
#мастермехендикиев #обучениемехендикиев
#школамехенди
#мехендитату
#мехендивпотоке
#мехендимедитация
#мехендирелакс… — Мехенди, хенд-мейд, живопись. Школа творческой жизни С-Арт
» Сложно, но очень интересно😁
❤
Запись на мехенди по тел/вайберу 067 4658732 #СветланаЗиновьева
#мехендикиев
#mehndi #hennaart
#красивоемехенди
#красивоемехендикиев
#мехендируки
#мехендигрудь
#мехендиспина
#мехендипоясница
#росписьхнойкиев
#татухнойкиев
#биотатукиев
#мастермехендикиев #обучениемехендикиев
#школамехенди
#мехендитату
#мехендивпотоке
#мехендимедитация
#мехендирелакс… — Мехенди, хенд-мейд, живопись. Школа творческой жизни С-АртСтереометрия Базовые понятия Определения Правильная пирамида
Стереометрия
Базовые понятия Определения • Правильная пирамида — это пирамида, у которой боковые рёбра равны, а в основании лежит правильный n-угольник • Правильный тетраэдр — это треугольная пирамида, все рёбра которой равны. • Объём пирамиды вычисляется по формуле: V = 1/3 Sh, где S — площадь основания, h — высота пирамиды • Прямая призма — это призма, боковые рёбра которой перпендикулярны плоскостям оснований. • Правильная n-угольная призма — это прямая призма, основанием которой служит правильный n-угольник. • Параллелепипед — это призма, основанием которой служит параллелограмм. • Объём призмы вычисляется по формуле: V = Sh, где S — площадь основания призмы, h — её высота.
• Правильная n-угольная призма — это прямая призма, основанием которой служит правильный n-угольник. • Параллелепипед — это призма, основанием которой служит параллелограмм. • Объём призмы вычисляется по формуле: V = Sh, где S — площадь основания призмы, h — её высота.
Как будем это рисовать?
Как будем это рисовать? Алгоритм • 1) рисуем основание пирамиды; • 2) строим центр основания, проводя медианы треугольника или диагонали квадрата; • 3) из центра ведём вверх высоту и отмечаем на ней вершину пирамиды; • 4) соединяем вершину пирамиды с вершинами основания.
Взаимное расположение прямых в пространстве Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут быть • пересекающимися, • параллельными • скрещивающимися.
Угол между скрещивающимися прямыми • Скрещивающиеся прямые не пересекаются. Можно ли в таком случае говорить об угле между ними?
Пример
Параллельность прямой и плоскости Как распознать случай параллельности прямой и плоскости? • Для этого имеется замечательно простое утверждение. Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости.
Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости.
Давайте посмотрим, как работает этот признак. • Пусть ABCA 1 B 1 C 1 — треугольная призма, в которой проведена плоскость A 1 BC
ОЧЕНЬ ВАЖНАЯ ТЕОРЕМА • Теорема о пересечении двух плоскостей, одна из которых проходит через прямую, параллельную другой плоскости.
Для чего она нужна? Пример • В правильной четырёхугольной пирамиде ABCDS (с вершиной S) точка M — середина ребра SC. Постройте сечение пирамиды плоскостью ABM
Перпендикулярность прямой и плоскости • Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Мы же не будем перебирать все прямые? ! Признак перпендикулярности прямой и плоскости. • Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Пример • Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны.
Рассказываю алгоритм)
Теорема о трёх перпендикулярах
Задача • Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны.
Угол между прямой и плоскостью
Задача • В правильном тетраэдре найдите угол между боковым ребром и плоскостью основания
Подходим к сечению • 1 • 2 • 3
Выводы по сечениям
Тоже оч важно • если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Угол между плоскостями (острый)
Задача • Найдите угол между двумя гранями правильного тетраэдра.
Расстояния — это перпендикуляры
Изложение темы «Тетраэдр» в учебнике «Геометрия» для 7-11 классов Погорелова А.В.
В другом базовом учебнике А.В. Погорелова и др.теоретический материал в той или иной степени касающийся темы «Тетраэдр» содержится в пунктах 176-180, 186, 192, 199, 200.
В пункте 180 “Правильные многогранники” содержится определение понятия «правильный тетраэдр» (“Тетраэдр представляет собой треугольную пирамиду, у которой все рёбра равны”), доказательство некоторых свойств и теорем о пирамиде проиллюстрировано чертежами тетраэдра. Однако в данном учебном пособии акцент на изучении фигуры не ставится, и в этом смысле его информативность (касательно тетраэдра) можно оценить как низкую. Практический же материал учебника содержит удовлетворительное количество заданий, касающихся пирамиды, в основании которой расположен треугольник (что по сути и есть тетраэдр). Приведём примеры решения некоторых задач.
Приведём примеры решения некоторых задач.
Решение задач.
Задача 1 (№ 41 из пункта «Многогранники»).
Основание пирамиды — равнобедренный треугольник, у которого основание равно 12 см, а боковая сторона — 10 см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Найдите высоту пирамиды.
Решение:
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABС. Тогда по теореме о трех перпендикулярах OK BC, ОМ АС и ON AB.
Тогда, SKO = SMO = SNO = 45° — как линейные углы данных двугранных углов. А следовательно, прямоугольные треугольники SKO, SMO иSNO равны по катету и острому углу. Так что OK=OM=ON, то есть точка О является центром окружности, вписаннойв ΔАВС.
Выразим площадь прямоугольника АВС:
(см)
С другой стороны, . Так что ; ОК=r=3 см. Так как в прямоугольном треугольнике SOK острый угол равен45°, то ΔSOK является равнобедренным и SO=OK=3(см).
Так что ; ОК=r=3 см. Так как в прямоугольном треугольнике SOK острый угол равен45°, то ΔSOK является равнобедренным и SO=OK=3(см).
Задача 2 (№ 43 из пункта «Объёмы многогранников»).
Найдите объем пирамиды, имеющий основанием треугольник, два угла которого a и β; радиус описанного круга R. Боковые ребра пирамиды наклонены к плоскости ее основания под углом γ.
Решение.
Так как все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды O1O проходит через центр описанной около основания окружности. Так что
Далее, в прямоугольном : .
В ΔАВС . Тогда согласно теореме синусов
.
Так что , , =
= .
Площадь треугольника :
.
Тогда .
Изложение темы «Тетраэдр» в учебнике «Геометрия» для 10-11 классов Александрова А. Д.
Д.
Рассмотрим учебное пособие Александрова А.Д. и др. «Геометрия: учебник для учащихся 11 кл. с углубленным изучением математики». Отдельных параграфов, посвящённых тетраэдру в этом учебнике нет, однако тема присутствует в виде фрагментов других параграфов.
Впервые тетраэдр упоминается в §21.3. В материале параграфа рассматривается теорема о триангуляции многогранника, в качестве примера выполняют триангуляцию выпуклой пирамиды. Само понятие «многогранник» в учебнике трактуется двумя способами, второе определение понятия напрямую связано с тетраэдром: «Многогранник – это фигура, являющаяся объединением конечного числа тетраэдров…». Познания, касающиеся правильной пирамиды и некоторых аспектов симметрии тетраэдра можно обнаружить в §23.
В §26.2 описано применение теоремы Эйлера («о правильных сетях») для правильных многогранников (в т.ч. для тетраэдра), а в §26.4 рассматриваются виды симметрий, характерные для этих фигур.
Формулу для нахождения объёма пирамиды авторы вводят в задаче №30. 1(2), а площадь боковой поверхности пирамиды вводится в материале параграфа «Площадь поверхности конуса и цилиндра» (§32.5).
1(2), а площадь боковой поверхности пирамиды вводится в материале параграфа «Площадь поверхности конуса и цилиндра» (§32.5).
Также, в учебнике можно найти информацию о средней линии тетраэдра, центре масс (§35.5) и классе равногранных тетраэдров. Движения I и II рода демонстрируются в ходе решения задач о тетраэдрах.
Отличительная особенность учебника — высокая научность, которую авторам удалось совместить с доступным языком и чёткой структурой изложения. Приведём примеры решения некоторых задач.
Решение задач.
Задача 1.
В данную правильную треугольную усечённую пирамиду с боковым ребром a можно поместить сферу, касающуюся всех граней, и сферу, касающуюся всех рёбер. Найдите стороны оснований пирамиды.
Решение.
Изобразим на чертеже «полную» пирамиду. Данная пирамида , — высота «полной» пирамиды, — ее часть до верхнего основания усеченной. Задача сводится к планиметрической, при этом не надо рисовать ни одной из данных сфер.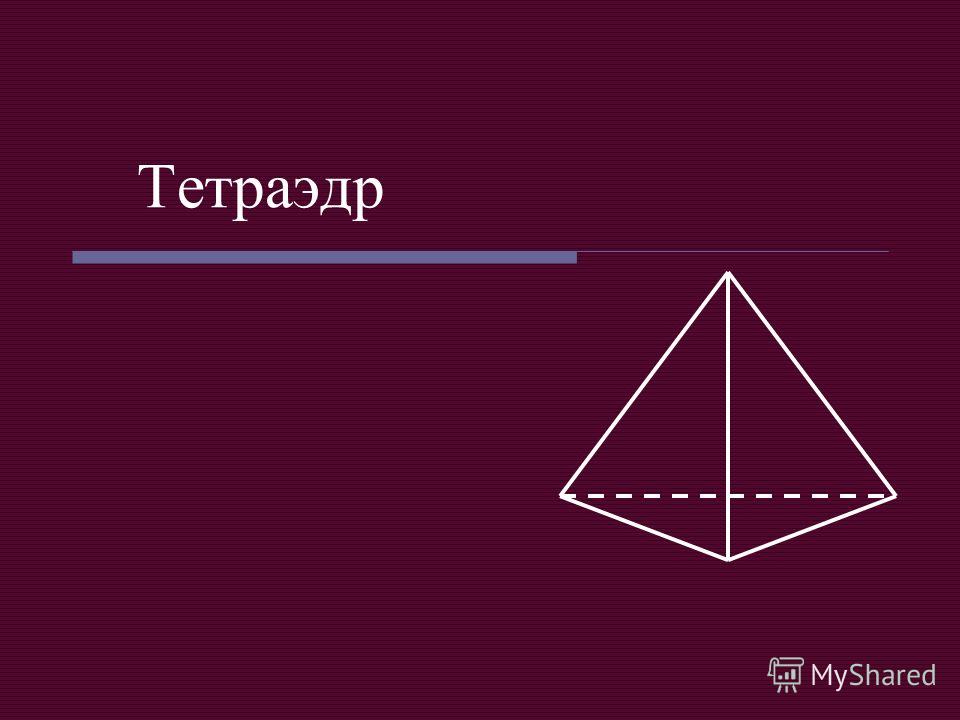 Т.к. в усеченную пирамиду можно вписать сферу, касающуюся всех ребер, то в её боковую грань можно вписать окружность. Обозначим , (для удобства деления пополам) и для описанного четырехугольника получим, что , откуда
Т.к. в усеченную пирамиду можно вписать сферу, касающуюся всех ребер, то в её боковую грань можно вписать окружность. Обозначим , (для удобства деления пополам) и для описанного четырехугольника получим, что , откуда
. (1)
Из существования вписанного шара следует, что существует полуокружность, расположенная в трапеции ( — апофема «полной» пирамиды) так, что ее центр лежит в середине , а сама она касается остальных трёх сторон трапеции.
— центр шара, и — точки касания. Тогда . Выразим эти величину через и . Из : . Из : . Из трапеции : . Получаем уравнение:
.(2)
Решив систему уравнений (1) и (2), получим, что стороны оснований равны .
Задача 2.
Внутри правильного тетраэдра с ребром a расположены четыре равные сферы так, что каждая сфера касается трех других сфер и трех граней тетраэдра. Найти радиус этих сфер.
Решение.
— данный тетраэдр, — его высота, — центры сфер, — точка пересечения прямой с плоскостью . Заметим, что центры равных сфер , касающихся плоскости , удалены от нее на равные расстояния, каждое из которых равно радиусу шара (обозначием его как x). Значит плоскости и параллельны, а потому .
Заметим, что центры равных сфер , касающихся плоскости , удалены от нее на равные расстояния, каждое из которых равно радиусу шара (обозначием его как x). Значит плоскости и параллельны, а потому .
Далее, каждая пара шаров касается между собой, а потому расстояние между центрами равно сумме их радиусов, то есть 2x . Имеем:
. Но как высота правильного тетраэдра с ребром ; как высота правильного тетраэдра с ребром 2x; .
Осталось выразить . Заметим, что точка находится внутри трехгранного угла и удалена от его граней на расстояние , а плоские углы трехгранного угла равны . Не сложно получить то, что . Приходим к уравнению:
, откуда после упрощений получаем .
Как сделать тетраэдр
Тема: учебные пособияОписание: Как нарисовать сетку тетраэдра, используя только линейку и циркуль, и сделать модель
Автор: Дэвид Колдуэлл, 15.04.20, 10:59
Тетраэдр
Тетраэдр Тетраэдр — это правильный четырехгранный многогранник.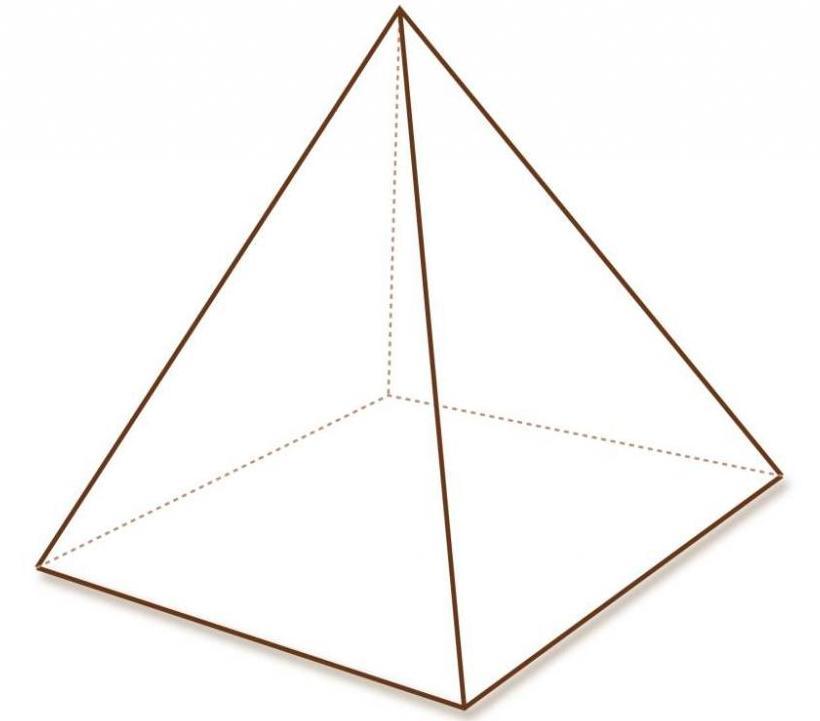 У него четыре угла, четыре грани и шесть краев. Она также известна как треугольная пирамида.
У него четыре угла, четыре грани и шесть краев. Она также известна как треугольная пирамида.
Что означает тетраэдр?
Тетраэдр — это греческое слово, буквально означающее четырехгранный.«Тетра» означает четыре, а «эдрон» — многоликая.
Латинское слово «четыре» — «Quad», как в «Четырехугольнике» или «Квадроцикле». Тетра по-гречески означает «четыре».
Платоническое тело
Тетраэдр — одно из пяти Платоновых Тел и представляет элемент Огня.
Тетраэдр уникален среди Платоновых Тел в том, что он имеет двойственность только с самим собой. Если вы соедините точку в центре каждой грани внутри, это создаст еще один тетраэдр.
Двойственность тетраэдра
Вы можете посмотреть видео к этому руководству на YouTube.
Пошаговое руководство по созданию модельного тетраэдра
Рисование сети тетраэдра
Шаг первый
- Используйте лист световой карты.

- Проведите горизонтальную линию поперек страницы линейкой или линейкой.
- Поместите кончик циркуля на линию, немного смещенную от центра, и нарисуйте круг.
- Переместите циркуль на пересечение линии и круга и нарисуйте второй круг, который перекрывает первый.
Шаг второй
- Поместите циркуль на пересечении линии и круга слева и нарисуйте дугу внутри левой окружности.
- Поместите циркуль на пересечении линии и круга слева и нарисуйте дугу внутри правого круга.
Шаг третий
- С помощью линейки нарисуйте три стороны равностороннего треугольника, который создается путем соединения точки, где два круга пересекаются наверху, и пересечения левой и правой дуг, созданных на втором шаге, проходящих через центральные точки двух кругов. .
Шаг четвертый
- Проведите две линии от центральных точек кругов до точки, где два круга пересекаются внизу.

Шаг пятый
- Нанесите чернила в сеть мелким карандашом и сотрите линии построения.
- Нарисуйте три выступа для приклеивания вашей модели.
Шаг шестой
- Осторожно вырежьте сеть ножом или ножницами.
- Сделайте надрез по внутренним линиям и выступам, чтобы их можно было сложить, чтобы получился аккуратный прямой край.
Шаг седьмой
- Сложите выступы и внутренние складки тетраэдрической сетки.
- Нанесите прозрачный клей ПВА вдоль выступов сетки.
Шаг восьмой
- Осторожно прижмите язычок к противоположной стороне и удерживайте, пока он не начнет прилипать. вы можете использовать малярный скотч, пока он высохнет.
- Повторяйте, пока все вкладки не будут склеены.
- Удерживайте модель пальцами, резинкой или липкой лентой, пока все стороны не будут склеены.
Ваша модель тетраэдра завершена
Ключевые слова: тетраэдр, сетка тетраэдров, модельный тетраэдр, что означает тетраэдр 1. Нарисуйте круг. Нарисуйте круг. | |
| 2.Поместите точку циркуля на край первого круга и нарисуйте еще один круг. | |
| 3. Поместите точку циркуля на перекресток и нарисуйте третий круг. | |
| 4. Нарисуйте отрезки линии, соединяющие все пересечения. (Используйте линейку. Вы можете нанести отметки по линиям шариковой ручкой.) | |
| 5. Четыре треугольника станут четырьмя гранями тетраэдра.Отметьте три выступа буквой T, как показано. (Вы будете использовать выступы, чтобы склеить края треугольников.) Заштрихованные участки вам не понадобятся. Аккуратно вырежьте вокруг белой области четыре треугольника и три выступа. | |
Примечание: Вы можете заметить, что вы использовали целый лист бумаги, чтобы создать довольно небольшую космическую форму. Если вы хотите сделать из одного листа бумаги тетраэдр как можно большего размера, вам совсем не обязательно рисовать на нем три полных круга.Раскройте циркуль пошире и разместите его, как показано, так, чтобы треугольники и выступы по-прежнему помещались на бумаге, но ненужные части кругов были обрезаны. Если вы хотите сделать из одного листа бумаги тетраэдр как можно большего размера, вам совсем не обязательно рисовать на нем три полных круга.Раскройте циркуль пошире и разместите его, как показано, так, чтобы треугольники и выступы по-прежнему помещались на бумаге, но ненужные части кругов были обрезаны. | |
| 6. После того, как вы вырежете фигуру, аккуратно сложите ее по каждой линии. (Если вы рисуете четкие линии шариковой ручкой, это «забивает» бумагу, чтобы ее было легче складывать. Кроме того, это помогает положить прямой край вдоль линии, когда вы складываете.) Сложите язычки вниз. Убедитесь, что вершина одного сложенного треугольника совпадает с острием треугольника под ним.Сгибайте каждую складку ногтем, стороной ручки или карандаша, чтобы каждая складка была очень четкой. | |
Если вы собираетесь украсить свою космическую форму, проще это сделать до того, как приклеить. (Обязательно украсьте чистую сторону, а не грязную сторону всеми изгибами и линиями.) (Обязательно украсьте чистую сторону, а не грязную сторону всеми изгибами и линиями.) |
Нарисуйте сеть тетраэдра по математике класса 10 CBSE
Подсказка: чтобы решить эту проблему, нам нужно понять определение сети и то, как выглядит тетраэдр.Геометрия — это двухмерная форма, которую можно сложить в трехмерное тело. Тетраэдр — это форма, состоящая из четырех равносторонних треугольников, соединенных общими ребрами. Тетраэдр еще называют треугольной пирамидой. Полный пошаговый ответ:
Чтобы нарисовать сеть, нам нужно понять значение сети. Геометрическая сетка — это двухмерная форма, которую можно сложить, чтобы сформировать трехмерную форму или твердое тело.
Тетраэдр — это твердое тело, состоящее из четырех треугольных граней, шести прямых ребер и четырех вершин.
Следовательно, чтобы построить сетку тетраэдров, нам нужно нарисовать четыре равносторонних треугольника.
Начнем с рисования равностороннего треугольника.
Начнем с рисования отрезка BC любой меры.
Это показано ниже,
Возьмите то же расстояние BC по циркулю и нарисуйте дугу с точкой B в качестве вершины.
Повторите ту же процедуру с циркулем на точке C.
Нам нужно убедиться, что обе дуги пересекаются друг с другом.
Назовите точку пересечения точкой A.
Это показано ниже,
Соедините отрезки AB и AC, и тогда у нас получится равносторонний треугольник ABC.
Это показано ниже,
Как мы знаем, у тетраэдра есть 4 треугольные грани. Нам нужно повторить этот процесс 4 раза.
Взяв за основу AC нужно начертить аналогичный равносторонний треугольник.
Это показано ниже,
Теперь повторите процесс в третий раз с DC в качестве базы.
Это показано ниже,
Теперь для последнего равностороннего треугольника мы возьмем за основу AD.
Повторяя процесс, мы получаем:
Итак, мы завершили процедуру рисования сетки для тетраэдра.

Чтобы склеить все части вместе, нам нужно добавить дополнительный вырез из бумаги.
Это можно представить следующим образом:
Следовательно, заштрихованная часть — это часть, которая будет удерживать трехмерное твердое тело вместе.
Следовательно, это необходимое решение.
Примечание: мы должны позаботиться о том, чтобы расстояние по компасу никогда не менялось и всегда было равно стороне требуемого равностороннего треугольника.{\ circ}} $.
Распространенные ошибки: рисование тетраэдрических атомов углерода
Как правильно рисовать тетраэдрические атомы углерода — и множество способов его испортить
Нарисовать правильные тетраэдры есть умение. И некоторые очень распространенные ошибки, которые могут быть не сразу очевидны.
Одна из проблем, с которой столкнулись химики со времен спорного (для 1870-х годов!) Предложения Вант-Хоффа о том, что атомы углерода, присоединенные к четырем заместителям, могут принимать тетраэдрическую геометрию, — это попытка изобразить трехмерные структуры на двух размерная страница.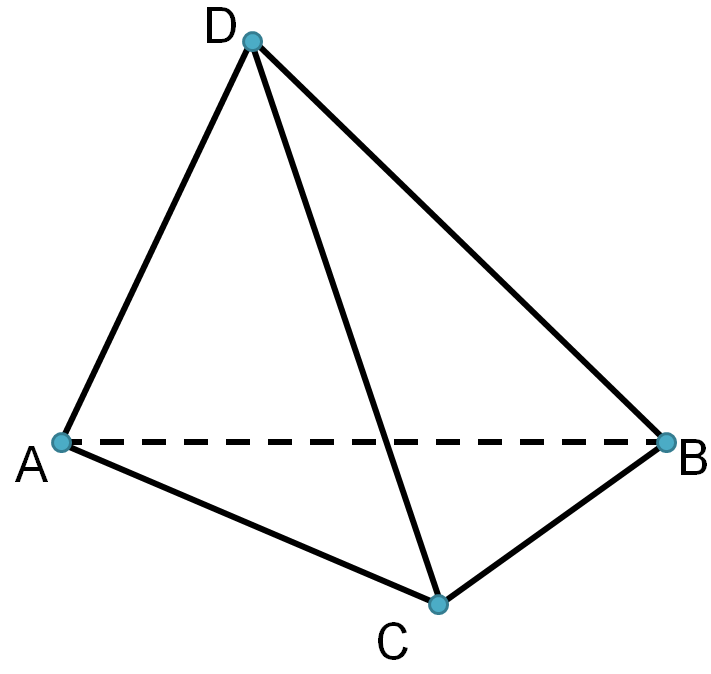
Содержание
- Клинья и тире: предметы на переднем плане имеют высокую контрастность; Элементы фона имеют низкую контрастность
- «Промышленный стандарт» способ рисования тетраэдрического углерода
- Повернутая версия того же самого
- Как испортить рисование тетраэдрического углерода, часть 1
- Второй способ испортить рисование тетраэдра Углерод
- Резюме: как рисовать тетраэдрический углерод (и как не делать этого)
1.Клинья и черточки: предметы на переднем плане имеют высокую контрастность; Элементы фона имеют низкую контрастность
В химии это делается с использованием тяжелых «клиньев» для изображения связей на переднем плане (указывающих на страницу) и легких «штрихов» для изображения связей на заднем плане (за страницей) ). Подумайте о том, как художники изображают горный хребет: чем дальше они находятся, тем слабее они нарисованы. [Веселая ссылка — посмотрите, сколько постеров фильма напоминают эту картину]
2. «Промышленный стандарт» способ рисования тетраэдрического углерода
«Промышленный стандарт» способ рисования тетраэдрического углерода Хотя существует несколько допустимых способов изобразить тетраэдрический углерод на плоской странице с помощью штрихов и клиньев, наиболее интуитивно понятным для понимания является тот, который показывает одну связь на «клине». , один на «тире» и два «плоских» (т. е. в плоскости страницы). Вот то, что вы могли бы назвать «отраслевой стандартной» версией, поскольку она позволяет нам легко добавлять цепочки, идущие влево и вправо (подробнее об этом позже).
Здесь обратите внимание, что на самом деле не имеет значения, , если «клиновидная» связь (C) нарисована слева или справа от «пунктирной» связи — они изображают одну и ту же молекулу!
3. Повернутая версия того же самого
Также часто показывают повернутые версии тетраэдрического углерода, например, в двух молекулах, изображенных ниже:
Еще раз обратите внимание, что клин и тире имеют острый угол между собой, как указано выше.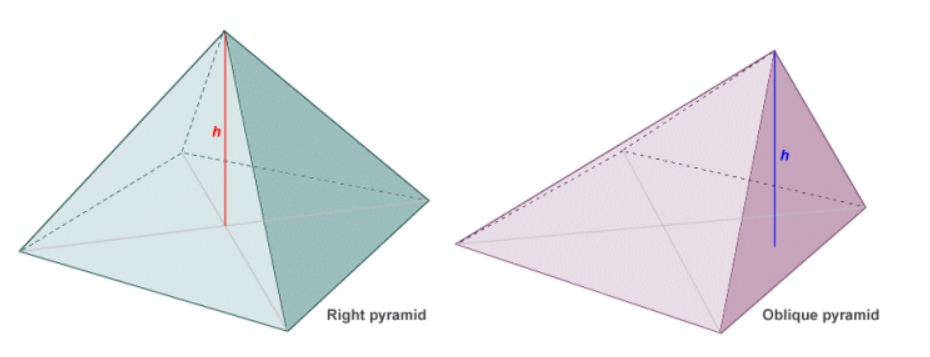
Хотя до сих пор это может показаться простым, может быть удивительно легко напортачить.
Один из наиболее распространенных способов сделать ошибку — это нарисовать тупой угол между «клином» и «тире» заместителями .
Проблема в том, что он не отображает тетраэдрическую геометрию. Фактически, если вы повернете молекулу на 90 °, вы увидите, что молекула на самом деле напоминает качели.
5. Второй способ ошибиться при рисовании тетраэдрического углеродаВторой способ неточно нарисовать тетраэдрический углерод — провести острый угол между двумя заместителями «в плоскости». Это неточно, потому что он показывает угол связи <90 ° для двух заместителей, что, конечно, нереально. Эта ошибка делает трехмерный чертеж ниже несколько неоднозначным.
Даже люди, которые должны знать, что они делают, иногда делают эти ошибки. Например, в этом видео Khan Academy углеродная цепь изображена следующим образом:
Например, в этом видео Khan Academy углеродная цепь изображена следующим образом:
Почему это плохо?
Хотя это не безвозвратно плохо, это вводит в заблуждение.
когда мы рисуем углеродную цепочку, предполагается, что все атомы углерода, нарисованные зигзагообразно, находятся «в плоскости».
Если бы мы хотели использовать неявные водороды, мы бы сделали это следующим образом.
Однако, если мы сделаем то же предположение с «плохим» рисунком выше, мы получим следующее:
И это неверно, потому что он неправильно отображает тетраэдрический углерод.Было бы намного хуже показать это в длинной цепочке, как здесь.
6. Резюме: Как нарисовать четырехгранный углерод (и как не делать этого)- Нарисуйте острый угол между клиньями и штрихами и тупой угол между заместителями в плоскости страницы .
Тот факт, что «на удивление легко» испортить рисование тетраэдрического углерода, на самом деле может удивить только новичков.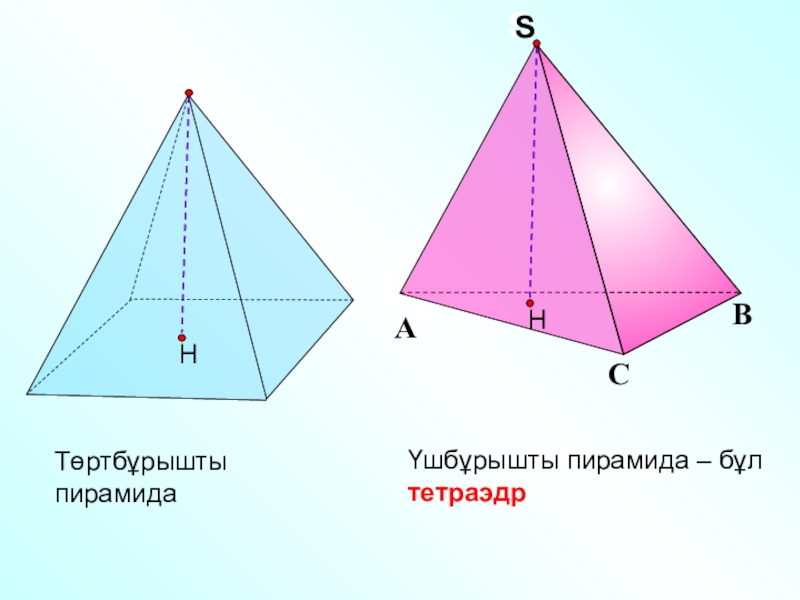 Опытные студенты знают, что органическая химия — это тема, которая предлагает поистине поразительное разнообразие способов ошибиться !!!
Опытные студенты знают, что органическая химия — это тема, которая предлагает поистине поразительное разнообразие способов ошибиться !!!
4.9: Трехмерные рисунки — Chemistry LibreTexts
Какова трехмерная форма молекулы?
Наша цель в этой главе — представить структуру молекулы. Когда мы рисуем структуру Льюиса для метана, это только двухмерное представление, но на самом деле соединение имеет трехмерную форму. Центральный углерод в метане тетраэдрический, с четырьмя атомами водорода в разных углах куба.
Мы можем нарисовать тетраэдр, образовав вершину между двумя линиями, а затем прикрепив клиновидную и штриховую линию к внешней стороне угла.Черная клиновидная линия читается как «этот атом направлен к нам». Штриховая линия читается как «этот атом дальше от нас». Хотя рисунок плоский, заштрихованные и клиновидные линии являются сокращенным обозначением трехмерности.
Изобразить трехмерную форму молекулы можно на бумаге, но только в том случае, если мы будем очень осторожны с условностями рисования, такими как рисунки клином и штрихом.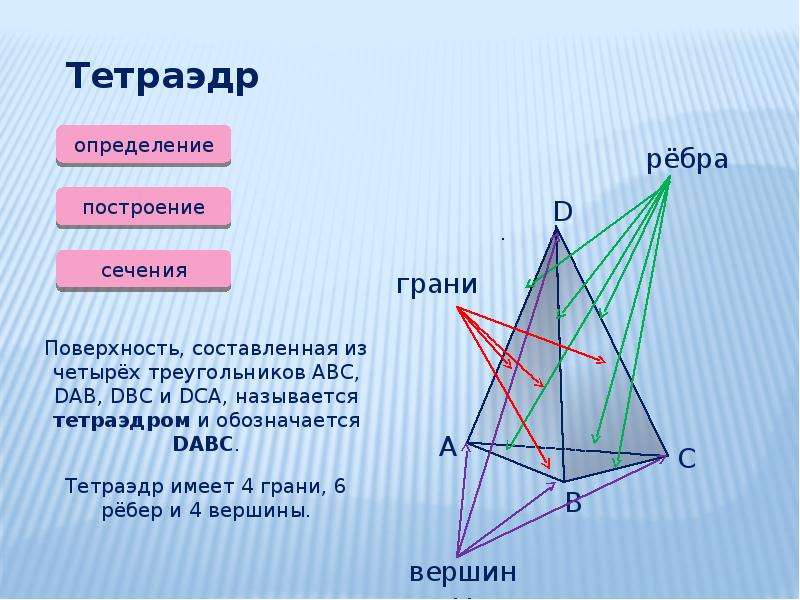
Углероды, которые связаны с четырьмя разными соседями, всегда тетраэдрически.Соседи, расположенные вокруг тетраэдрического углерода, разнесены примерно на 109 °. Иногда, по причинам, которые мы здесь не будем вдаваться, тетраэдрические атомы углерода называют sp3-атомами углерода.
Пентан — это соединение, содержащее четыре тетраэдрических атома углерода подряд. Каждый тетраэдрический углерод можно было показать в виде клиновидных выступов.
Также очень распространено использование компьютерных программ для рисования, чтобы показать формы молекул. Вы можете рассматривать трехмерную структуру пентана по-разному.Здесь показаны три наиболее распространенных способа. Ball & Stick — это простой способ увидеть, где находятся все атомы и как они связаны. Каркас позволяет видеть соединения, не закрывая обзор атомами. Модели, заполняющие пространство, призваны наиболее точно показать вам форму молекулы, хотя при этом участвующие в ней атомы не видны.
Перейти к Анимация IM9.1. Трехмерная модель пентана.
Углероды, связанные двойной связью с одним соседом и, следовательно, с тремя разными соседями в целом, являются тригонально плоскими.Соседи находятся в одной плоскости и находятся на расстоянии около 120 ° друг от друга. Тригональные плоские атомы углерода иногда называют атомами углерода sp2.
Пропен имеет два тригональных плоских атома углерода, а также один тетраэдрический атом углерода. Обратите внимание, что тригональный плоский углерод плоский, если смотреть с одного направления, но не с другого. Иногда вы увидите, что тригональные атомы углерода нарисованы по-разному, если ящик хочет, чтобы вы смотрели на молекулу с того или иного направления.
Посмотрите, сможете ли вы найти оба вида карбона в представленной ниже модели.
Перейти к Анимация IM9.2. Трехмерная модель пропена.
Углероды, у которых есть только два разных соседа, линейны; каждый сосед находится на 180 ° друг от друга. Линейные атомы углерода иногда называют sp-атомами углерода.
Линейные атомы углерода иногда называют sp-атомами углерода.
Пропин имеет два линейных атома углерода, а также один тетраэдрический атом углерода. Посмотрите, сможете ли вы найти оба вида карбона в представленной ниже модели.
Перейти к Анимация IM9.3. Трехмерная модель пропина.
Сказать, что углерод — это sp или sp2, мы только придадим форму одному атому в молекуле. Сама молекула может иметь особую форму, которая определяется геометрией составляющих ее атомов, но которую нельзя просто описать словами как «тетраэдрическая» или «линейная».
Пентан имеет примерно зигзагообразную форму. В модели, заполняющей пространство, он напоминает медленно движущуюся толстую гусеницу. Пропен имеет форму бумеранга. Пропин имеет форму дротика; у него есть заостренный конец и оперенный конец.
Другие молекулы имеют более сложную форму. Форму гинкголида B (натурального продукта, выделенного из дерева ginkgo biloba , представляющего интерес с медицинской точки зрения) описать сложно. Однако ясно, что отдельные атомы углерода в гинкголиде B в основном тетраэдрические, с парой плоских тригональных атомов.
Однако ясно, что отдельные атомы углерода в гинкголиде B в основном тетраэдрические, с парой плоских тригональных атомов.
Перейти к Анимация IM9.4. Трехмерная модель гинкголида Б.
Понимание общей формы молекулы особенно важно в различных аспектах биохимии.Например, действие любого лекарства в организме сильно зависит от формы лекарства и от того, как эта форма может взаимодействовать с конкретными рецепторами.
Проблема IM9.1 . Цис- и трансциклические изомеры имеют два заместителя, присоединенные к кольцу. Цис-изомер имеет оба заместителя на одной стороне кольца. Транс-изомер имеет заместители на противоположных сторонах кольца. Используйте клиновидные проекции, чтобы нарисовать формы следующих молекул:
a) цис -1,2-дихлорциклопропан, C 3 H 4 Cl 2 (числа означают, что на первом углероде присутствует хлор, а на втором — хлор)
b) транс -1,2-дихлорциклопропан, C 3 H 4 Cl 2 c) цис -1,3-дибромциклобутан, C 4 H 6 Br 2 d ) транс -1,3-дибромциклобутан, C 4 H 6 Br 2
Проблема IM9.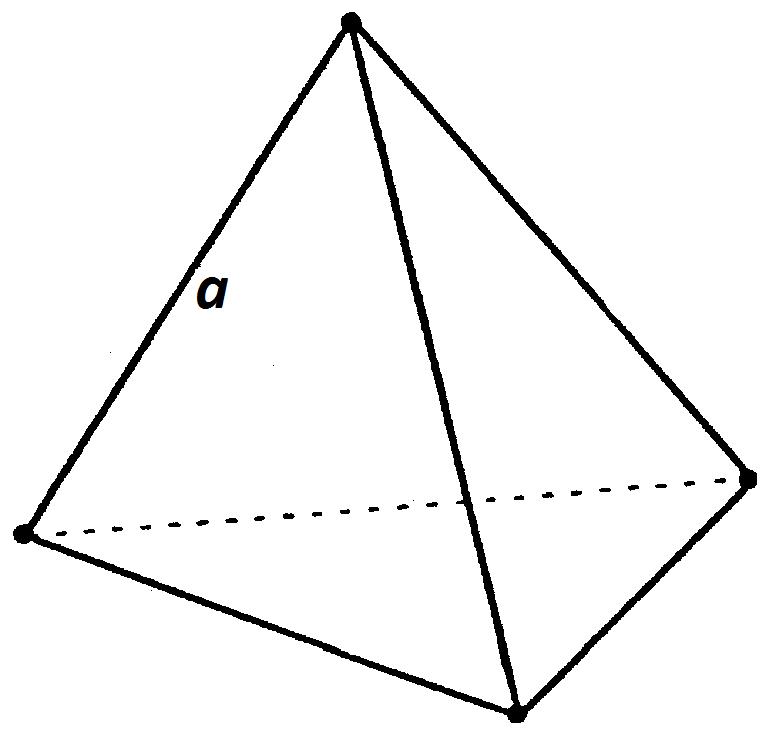 2. Определите геометрию указанных атомов углерода в следующих молекулах:
2. Определите геометрию указанных атомов углерода в следующих молекулах:
РЕШЕНИЕ: Изобразите тетраэдрическое представление (S) -2-пентанола (2-гидроксипентана).
Стенограмма видео
они хотят нарисовать в Tetra Futral представление туннеля s to pin. Итак, вперед и вперед. Что мы, очевидно, подготовили для этого? Что ж, у нас есть Пенн Тан. Итак, это будет пять членов сети, которые собираются вытащить этот кошелек из 123 или пяти, а затем говорится, что у нас есть алкоголь.Так что давай просто выйдем и положим это вот так. И тогда мы знаем, что эта машина должна быть. Итак, у нас здесь также есть водород. Итак, теперь нам нужно решить. Что будет сзади, этот спирт или водород? Что ж, давайте просто предположим, что алкоголь находится в самом начале. Итак, я должен был выглядеть вот так. Итак, когда мы сравниваем эти группы здесь, ну, у водорода самые низкие атомные номера. Должно быть четыре. И сравнивая эти два углерода, сказал, что этот кислород, кислород имеет более высокий атомный номер..svg/1280px-Pentagonal_Pyramid_(Hexahedron).svg.png) Итак, у нас это есть. Теперь нам нужно вывести по два атома углерода с каждой стороны. Итак, у этого углерода их три. Присоединяется водород. Этот углерод состоит из двух атомов водорода и одного углерода. Поэтому переход вправо имеет более высокий приоритет, а переход влево — более низкий. Так что посмотрим. Итак, когда мы вращаемся здесь, так как четыре уже находятся сзади, мы хотели бы повернуть от 1 до 3 вот так. Итак, это идет вправо. Насколько я помню, когда вы рисуете заглавную букву, чтобы нарисовать эту маленькую петлю, вам нужно идти вправо, чтобы это было нашим, но мы хотели s.Это означает, что мы действительно хотим, чтобы спирт находился сзади, а водород и спереди. Так что это просто быстрый способ сделать это. Всегда. Просто поместите нижнюю группу свойств сзади, если можете. А затем, если тот не работает, просто переключите свои центры Кирилла, и тогда он даст вам другой в Антамеру для него или другой центр Кирилла, так что это будет трехмерное или четырехмерное изображение, которое он бросил.
Итак, у нас это есть. Теперь нам нужно вывести по два атома углерода с каждой стороны. Итак, у этого углерода их три. Присоединяется водород. Этот углерод состоит из двух атомов водорода и одного углерода. Поэтому переход вправо имеет более высокий приоритет, а переход влево — более низкий. Так что посмотрим. Итак, когда мы вращаемся здесь, так как четыре уже находятся сзади, мы хотели бы повернуть от 1 до 3 вот так. Итак, это идет вправо. Насколько я помню, когда вы рисуете заглавную букву, чтобы нарисовать эту маленькую петлю, вам нужно идти вправо, чтобы это было нашим, но мы хотели s.Это означает, что мы действительно хотим, чтобы спирт находился сзади, а водород и спереди. Так что это просто быстрый способ сделать это. Всегда. Просто поместите нижнюю группу свойств сзади, если можете. А затем, если тот не работает, просто переключите свои центры Кирилла, и тогда он даст вам другой в Антамеру для него или другой центр Кирилла, так что это будет трехмерное или четырехмерное изображение, которое он бросил. для s к пину Tittel
для s к пину Tittel
шагов для извлечения тетраэдра в Google SketchUp
Создавать крыши в Google SketchUp в 3D довольно просто, но иногда вам нужно больше информации об угле обрамления крыши из ваших чертежей.Вот пошаговый пример извлечения тетраэдра из трехмерного рисунка в Google SketchUp. В этом примере мы будем использовать трапециевидную древесину, созданную из подключаемого модуля Roof Framing Geometry на основе Skewed Rafter на стр. 52 в «Traité Théorique et Pratique de Charpente» Луи Мазероля. Это извлечение тетраэдра также является примером «trait carré», рисующий перпендикулярную линию к заданной линии.Шаг 1.
С помощью транспортира нарисуйте перпендикулярную вспомогательную линию «trait carré» на верхнем крае стропила от точки E.
Шаг 2. Проведите линию от точки E до точки C, а затем удалите вспомогательную линию, созданную транспортиром.
Шаг 3. С помощью транспортира нарисуйте перпендикулярную вспомогательную линию, trait carré, на стороне стропила в точке C. Затем проведите линию от точки C к точке A и затем удалите вспомогательную линию, созданную транспортиром. .
Затем проведите линию от точки C к точке A и затем удалите вспомогательную линию, созданную транспортиром. .
Шаг 4. Выделите 3 верхних ребра тетраэдра. Линия E-C, линия C-B и линия C-A.Используйте Edit / Copy, затем Edit / Plaste.
Шаг 5. Проведите линию от E-A и проведите линию от A до B, чтобы завершить края тетраэдра.
Шаг 6. Используя инструмент «Ведро с краской», нарисуйте грани тетраэдра. Затем проверьте углы на извлеченном тетраэдре, чтобы убедиться, что они совпадают с углами стропила.
Шаг 7. Чтобы нарисовать тетраэдр в развернутом виде, начните с построения вспомогательной линии в точке B под углом EBC.
Шаг 8.Проведите вспомогательную линию в точке E, используя угол BEC. Затем нарисуйте вспомогательные линии с помощью инструмента «Линия» и затем удалите вспомогательные линии, созданные с помощью транспортира.
Шаг 9. Проведите вспомогательную линию в точке C, используя угол ECA. Нарисуйте вспомогательную линию в точке E, используя угол CEA. Затем нарисуйте вспомогательные линии с помощью инструмента «Линия» и затем удалите вспомогательные линии, построенные с помощью транспортира.
Нарисуйте вспомогательную линию в точке E, используя угол CEA. Затем нарисуйте вспомогательные линии с помощью инструмента «Линия» и затем удалите вспомогательные линии, построенные с помощью транспортира.
Иногда вам нужно использовать транспортир в другом месте, чтобы нарисовать правильный угол.После того, как вы нарисовали правильный угол с помощью транспортира, используйте инструмент перемещения, чтобы разместить вспомогательную линию в правильном положении.
Шаг 10. Проведите вспомогательную линию в точке E, используя угол CEB. Это помогает закрасить грани треугольников, чтобы транспортир правильно расположил себя на грани треугольника. Нарисуйте вспомогательную линию в точке A, используя угол EAB. Затем проведите по вспомогательным линиям с помощью инструмента «Линия» и затем удалите вспомогательные линии, построенные с помощью транспортира.Затем раскрасьте грань треугольника.
Шаг 11. Проведите вспомогательную линию перпендикулярно линии EA. Затем с помощью инструмента «Перемещение» разместите вспомогательную линию в точке C.
Затем с помощью инструмента «Перемещение» разместите вспомогательную линию в точке C.
Шаг 12. Проведите вспомогательную линию перпендикулярно линии AC. Нарисуйте угол ВАС в точке А.
Шаг 13. Используйте рулетку и определите длину линии CB. Затем снова используйте рулетку вдоль вспомогательной линии в точке C, чтобы отметить длину CB.В программе 2D Cad мы могли бы использовать инструмент «Дуга» или «Круг», чтобы отметить местоположение новой точки, но не в Google SketchUp. Затем проведите линию от D до новой точки B. Треугольник DCB — это треугольник, который мы будем использовать в следующем посте о тетраэдрах.
.

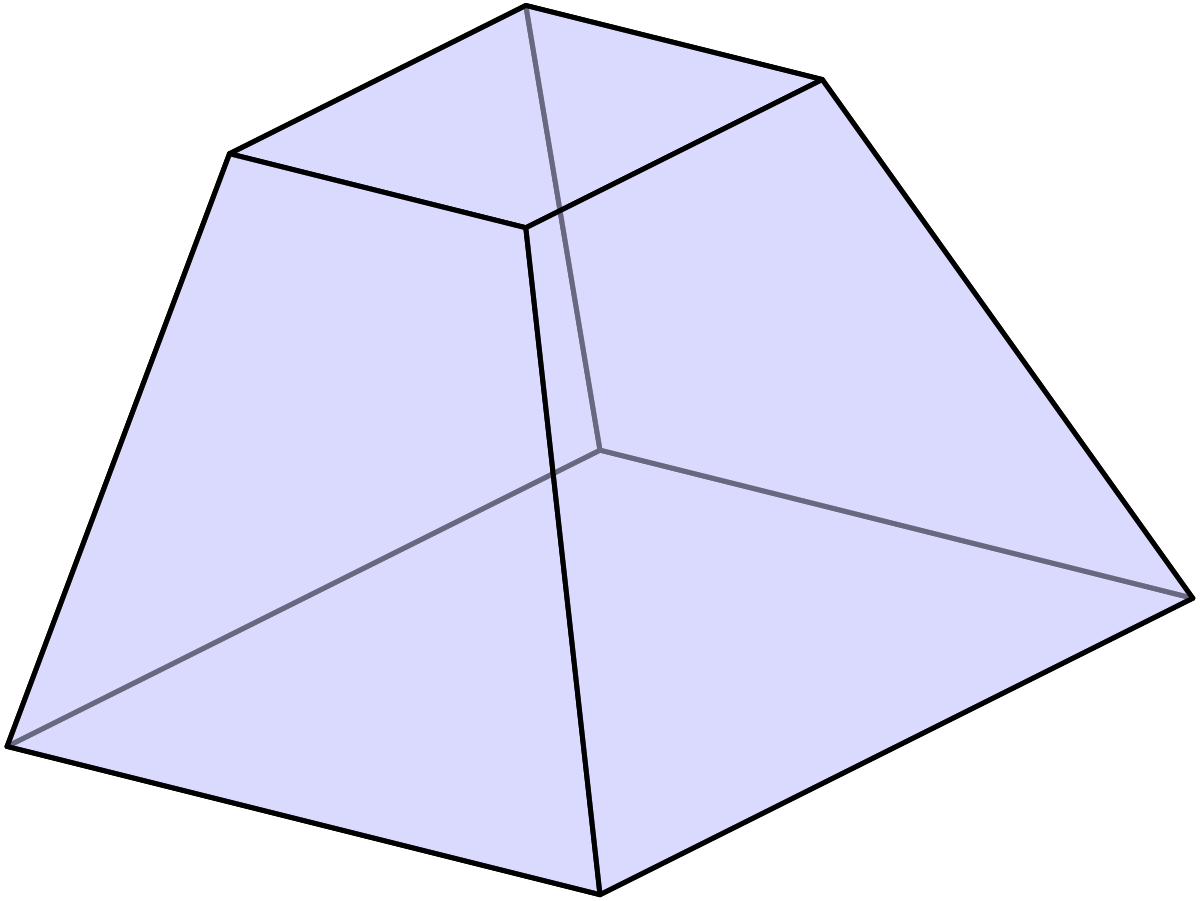 ..).
..).