Как нарисовать соты: Как нарисовать улей для пчел, соты карандашом или красками поэтапно?

учимся пользоваться редактором фигур от создания линий до схем

MS Office Word 2007 и 2010 — текстовые редакторы, чрезвычайно распространенные в пользовательской среде. Но о том, как рисовать в Ворде, знают далеко не все владельцы ПК. Являясь довольно универсальными пакетами, приложения в основном используются для создания текстовых документов. Иногда чуть более продвинутые пользователи вставляют в них картинки, но мало кому известно, что рисунок в MS Word можно создать, не прибегая к помощи других редакторов. Как нарисовать картинку в MS Word 2007 и 2010? После первого же урока по рисованию в популярном редакторе вы сможете стать хорошим иллюстратором.

Как открыть меню рисования в MS Office Word?

Стандартное меню для вставки фигур поможет создать ваш рисунок в ворде

Перед тем как нарисоватьв Ворде картинку, следует открыть на ленте закладку «Вставка». Ее просто найти, так как закладка находится правее кнопки «Главная». Под закладкой открывается меню «Иллюстрации», которым можно пользоваться при вставке в документ картинок из файлов, библиотек, сайта Microsoft и т.

д. Тем не менее, чтобы рисовать в Ворде, нужно открыть вкладку «Фигуры». Под ней скрывается целый набор инструментов для рисунка в Ворде, а в конце списка находится команда «Новое полотно». Выполнив команду, получаем в документе поле для работы, где рисуем самые различные фигуры, предлагаемые в контекстном меню. Здесь есть линии и шаблоны различной конфигурации. Как создать полотно для работы, видно из схемы (рис. 1). Размеры полотна для изображений вы можете отрегулировать по своему усмотрению.

Рисование схем и изображений с помощью шаблонов фигур

Если вы еще не совсем понимаете, как сделать линию в Ворде, воспользуйтесь готовыми шаблонами, которые помогут создать схему в Ворде или сделать геометрический рисунок. Чтобы они оказались на полотне, достаточно кликнуть по выбранному шаблону левой кнопкой мыши. Второй раз щелчок левой кнопкой делается на поле изображения. Получившееся изображение можно редактировать, так как после его вставки появляются команды «Изменить фигуру», «Заливка фигуры», «Контур» и «Эффекты фигур».

Открыв первое из перечисленных меню, можно изменить конфигурацию рисунка, пользуясь второй и третьей вкладками. Можно задать цвет фону изображения и его границам. Помимо того, можно отредактировать толщину контура, сделать его прерывистым и т. п. Четвертое меню предлагает украсить картинку эффектами. С его помощью рисуем тень, придаем геометрической части плоскости полупрозрачность и даже видимость трехмерности.

Рисование и редактирование линий

То, как сделать линию в Ворде, интересует всех, кто хочет сопроводить документ не шаблонной, а оригинальной иллюстрацией. MS Office Word поможет начертить ровные отрезки, векторные линии, которые обязательно пригодятся при составлении схем.

Есть в редакторе команды, подобные «Рисунку карандашом» или «Лассо» в Photoshop

. Как рисовать ими? Все очень просто! Выбирайте в меню команды «Полилиния» и «Рисованная кривая», кликайте по выбранной левой кнопкой мыши и делайте повторный клик на полотне. Не отпуская кнопки, делайте нужный рисунок. А еще одним нажатием на мышь картинка фиксируется на поле. Ее, как и шаблоны, можно отредактировать, заливая различными цветами, создавая эффекты и т. п. А с помощью «Изменения фигуры» вы подправите изображение по периметру.

Теперь вам стало яснее, как рисовать в MS Office Word. Необходимо сказать, что полноценной программой для рисования текстовый редактор считать нельзя, но с помощью функции создания изображений вы можете значительно сократить время при иллюстрировании документов.

Занимательная математика. Правильный шестиугольник

Не знаю уж в силу чего, но у меня иногда возникает навязчивая идея решить ту или иную задачу из школьного/институтского курсов по математике или программированию. Обычно (пока что) это что-то достаточно простое. Интересен сам процесс получения результата на основе тех знаний, которые есть в голове на данный момент. 

Как-то раз зашел разговор о сотах, пчелиных сотах. Раньше я не особо задумывался о том, что сота представляет собой правильный шестиугольник. Не то что не знал, а просто не думал о том, как эти маленькие создания сами(!) создают такую структуру, состоящую из абсолютно правильных шестиугольников… Задачка пришла сама собой — нарисовать правильный шестиугольник, как водится, только с использованием циркуля и линейки.

Шаг 1. Рисуем окружность, в которую будет вписан наш шестиугольник

Шаг 1

Шаг 2. Докажем, что сторона правильного шестиугольника равна радиусу окружности, в которую он вписан.

Шаг 2

Док-во: Исходя из условий (и признаков рав-ва треугольников), понимаем, что все три треугольники в верхней части рисунка — равны между собой. Соотв. угол Альфа = 60° (180 / 3), а это значит, что треугольник равносторонний (на остальные углы в треугольнике приходится по 120° и они так же равны между собой, как прилежащие к равным сторонам треугольника) и, соотв. сторона шестиугольника равна радиусу.

Шаг 3

Шаг 3. Строим шестиугольник: ставим циркуль в произвольное место на окружности, откладываем радиус на окружности, переносим циркуль в только что поставленную метку, делаем засечку дальше и так еще 4 раза, пока не придем в исходную точку. При помощи линейки соединяем полученные точки. Вуаля.

P.S. Иллюстрации сделаны на планшете, поэтому не придирайтесь  картинка с сотами взята из инета (google.com, поиск: пчелиные соты)

Контакты:

Создание сеток шестиугольников / Хабр

Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я

коллекционирую ресурсы о сетках шестиугольников

уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (

Charles Fu

) и Кларка Вербрюгге (

Clark Verbrugge

). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты.

(Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.)

.

Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.

Геометрия

Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину. Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.

Шестиугольники с плоским (слева) и острым (справа) верхом

У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек.

Каждая угловая точка общая для трёх шестиугольников. Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).

Углы

В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка

i

находится на расстоянии

(60° * i) + 30°

, на

size

единиц от центра

center

. В коде:

function hex_corner(center, size, i):
    var angle_deg = 60 * i   + 30
    var angle_rad = PI / 180 * angle_deg
    return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))

Для заполнения шестиугольника нужно получить вершины многоугольника с

hex_corner(…, 0)

по

hex_corner(…, 5)

. Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в

hex_corner(…, 0)

.

Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.

Углы шестиугольников с плоским и острым верхом

Размер и расположение

Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника

height = size * 2

. Вертикальное расстояние между соседними шестиугольниками

vert = height * 3/4

.

Ширина шестиугольника width = sqrt(3)/2 * height. Горизонтальное расстояние между соседними шестиугольниками horiz = width.

В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.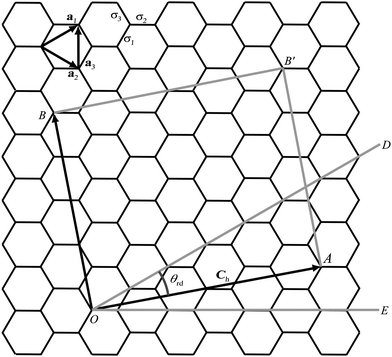

Системы координат

Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.

Координаты смещений

Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются

col

или

q

. Строки обозначаются

row

или

r

. Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.

Горизонтальное расположение «нечет-r»

Горизонтальное расположение «чёт-r»

Вертикальное расположение «нечет-q»

Вертикальное расположение «чёт-q»

Кубические координаты

Ещё один способ рассмотрения сеток шестиугольников — видеть в них

три

основные оси, а не

две

, как в сетках квадратов. В них проявляется элегантная симметрия.

Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0. Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.

Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.

Шестиугольники
Кубы

Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.

Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.

1. Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z, равным 0, 1, 2, 3, чтобы увидеть связь. Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
2. Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z, поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.

Кубические координаты — разумный выбор для системы координат сетки шестиугольников. Условием является

x + y + z = 0

, поэтому в алгоритмах оно должно сохраняться. Условие также гарантирует, что для каждого шестиугольника всегда будет каноническая координата.

Существует множество различных систем координат для кубов и шестиугольников. В некоторых из них условие отличается от x + y + z = 0. Я показал только одну из множества систем. Можно также создать кубические координаты с x-y, y-z, z-x, у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.

Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.

Осевые координаты

Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие

x + y + z = 0

, третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.

Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x, а r соответствует z, но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.

Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0, мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q, r, s, поэтому условие выглядит как q + r + s = 0, и я, когда нужно, могу вычислить s = -q - r.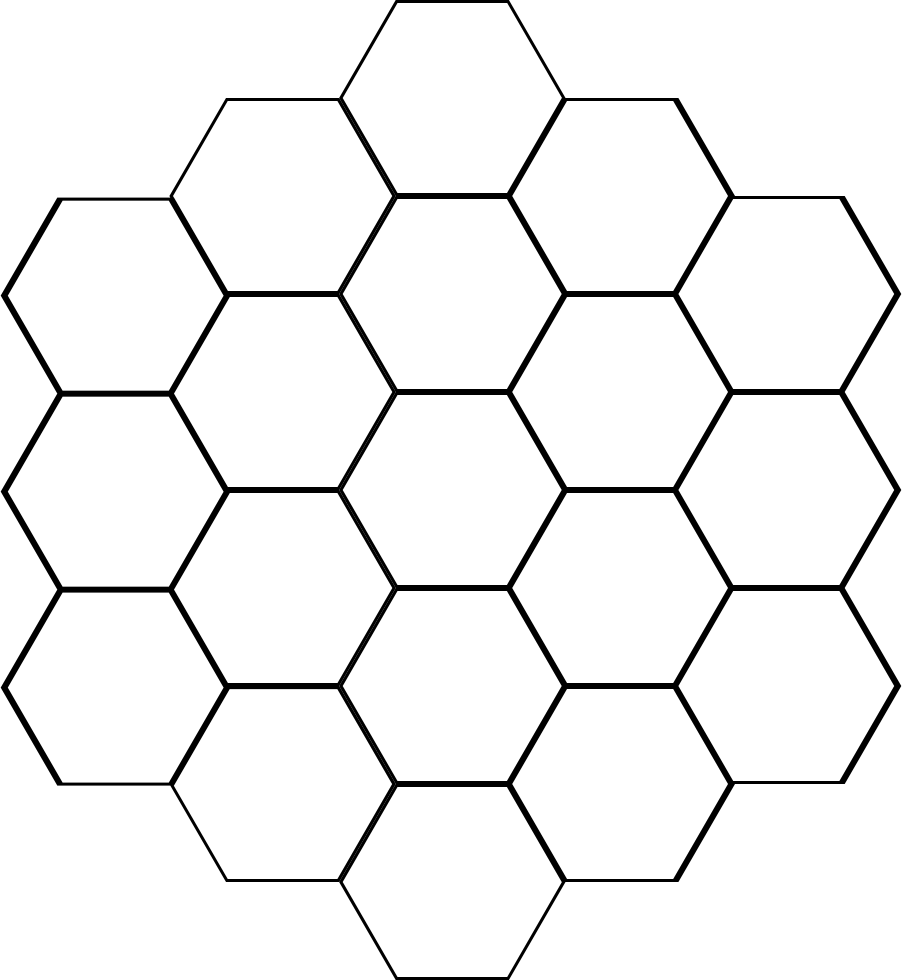

Оси

Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.

Координаты смещения, кубические и осевые

Ось — это направление, в котором соответствующая координата увеличивается. Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.

Преобразование координат

Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.

Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:

# преобразование кубических в осевые координаты
q = x
r = z

# преобразование осевых в кубические координаты
x = q
z = r
y = -x-z

В коде эти две функции могут быть записаны следующим образом:

function cube_to_hex(h): # осевая
    var q = h.x
    var r = h.z
    return Hex(q, r)

function hex_to_cube(h): # кубическая
    var x = h.q
    var z = h.r
    var y = -x-z
    return Cube(x, y, z)

Координаты смещения совсем немного сложнее:

# преобразование кубических в смещение чёт-q
col = x
row = z + (x + (x&1)) / 2

# преобразование смещения чёт-q в кубические
x = col
z = row - (col + (col&1)) / 2
y = -x-z

# преобразование кубических в смещение нечет-q
col = x
row = z + (x - (x&1)) / 2

# преобразование смещения нечет-q в кубические
x = col
z = row - (col - (col&1)) / 2
y = -x-z

# преобразование кубических в смещение чёт-r
col = x + (z + (z&1)) / 2
row = z

# преобразование чёт-r в кубические
x = col - (row + (row&1)) / 2
z = row
y = -x-z

# преобразование кубических в нечет-r
col = x + (z - (z&1)) / 2
row = z

# преобразование нечет-r в кубические
x = col - (row - (row&1)) / 2
z = row
y = -x-z

Примечание о реализации: я использую a&1 (

побитовое «И»

) вместо a%2 (

деления с остатком

) для определения, является ли число чётным (0) или нечётным (1). Подробное описание см.

на странице примечаний к моей реализации

.

Соседние шестиугольники

Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.

Кубические координаты

Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат

Cube(dx, dy, dz)

во время компиляции:

var directions = [
   Cube(+1, -1,  0), Cube(+1,  0, -1), Cube( 0, +1, -1),
   Cube(-1, +1,  0), Cube(-1,  0, +1), Cube( 0, -1, +1)
]

function cube_direction(direction):
    return directions[direction]

function cube_neighbor(hex, direction):
    return cube_add(hex, cube_direction(direction))

Осевые координаты

Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу

Cube(dx, dy, dz)

и преобразуем в таблицу

Hex(dq, dr)

:

var directions = [
   Hex(+1,  0), Hex(+1, -1), Hex( 0, -1),
   Hex(-1,  0), Hex(-1, +1), Hex( 0, +1)
]

function hex_direction(direction):
    return directions[direction]

function hex_neighbor(hex, direction):
    var dir = hex_direction(direction)
    return Hex(hex.q + dir.q, hex.r + dir.r)

Координаты смещения

В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.

Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row. Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2). Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.

Нечет-r

var directions = [
   [ Hex(+1,  0), Hex( 0, -1), Hex(-1, -1),
     Hex(-1,  0), Hex(-1, +1), Hex( 0, +1) ],
   [ Hex(+1,  0), Hex(+1, -1), Hex( 0, -1),
     Hex(-1,  0), Hex( 0, +1), Hex(+1, +1) ]
]

function offset_neighbor(hex, direction):
    var parity = hex.row & 1
    var dir = directions[parity][direction]
    return Hex(hex.col + dir.col, hex.row + dir.row)

Сетка для чётной (EVEN) и нечётной (ODD) строк

Чёт-r

var directions = [
   [ Hex(+1,  0), Hex(+1, -1), Hex( 0, -1),
     Hex(-1,  0), Hex( 0, +1), Hex(+1, +1) ],
   [ Hex(+1,  0), Hex( 0, -1), Hex(-1, -1),
     Hex(-1,  0), Hex(-1, +1), Hex( 0, +1) ]
]

function offset_neighbor(hex, direction):
    var parity = hex.row & 1
    var dir = directions[parity][direction]
    return Hex(hex. col + dir.col, hex.row + dir.row)

Сетка для чётной (EVEN) и нечётной (ODD) строк

Нечет-q

var directions = [
   [ Hex(+1,  0), Hex(+1, -1), Hex( 0, -1),
     Hex(-1, -1), Hex(-1,  0), Hex( 0, +1) ],
   [ Hex(+1, +1), Hex(+1,  0), Hex( 0, -1),
     Hex(-1,  0), Hex(-1, +1), Hex( 0, +1) ]
]

function offset_neighbor(hex, direction):
    var parity = hex.col & 1
    var dir = directions[parity][direction]
    return Hex(hex.col + dir.col, hex.row + dir.row)

Сетка для чётного (EVEN) и нечётного (ODD) столбцов

Чёт-q

var directions = [
   [ Hex(+1, +1), Hex(+1,  0), Hex( 0, -1),
     Hex(-1,  0), Hex(-1, +1), Hex( 0, +1) ],
   [ Hex(+1,  0), Hex(+1, -1), Hex( 0, -1),
     Hex(-1, -1), Hex(-1,  0), Hex( 0, +1) ]
]

function offset_neighbor(hex, direction):
    var parity = hex.col & 1
    var dir = directions[parity][direction]
    return Hex(hex.col + dir.col, hex.row + dir. row)

Сетка для чётного (EVEN) и нечётного (ODD) столбцов

Использование вышеуказанных таблиц подстановки — это простейший способ вычисления соседей. Если вам интересно, можно также почитать об извлечении этих чисел.

Диагонали

Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).

var diagonals = [
   Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1), 
   Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1)
]

function cube_diagonal_neighbor(hex, direction):
    return cube_add(hex, diagonals[direction])

Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.

Расстояния

Кубические координаты

В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов. Это делает расчёт расстояний простым. В сетке квадратов

манхэттенские расстояния

равны

abs(dx) + abs(dy)

. В сетке кубов манхэттенские расстояния равны

abs(dx) + abs(dy) + abs(dz)

. Расстояние в сетке шестиугольников равно их половине:

function cube_distance(a, b):
    return (abs(a.x - b.x) + abs(a.y - b.y) + abs(a.z - b.z)) / 2

Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:

function cube_distance(a, b):
    return max(abs(a.x - b.x), abs(a.y - b.y), abs(a.z - b.z))

На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.

GIF

Осевые координаты

В осевой системе третья координата выражена неявно. Давайте

преобразуем

из осевой в кубическую систему для расчёта расстояния:

function hex_distance(a, b):
    var ac = hex_to_cube(a)
    var bc = hex_to_cube(b)
    return cube_distance(ac, bc)

Если компилятор в вашем случае встраивает (inline)

hex_to_cube

и

cube_distance

, то он сгенерирует такой код:

function hex_distance(a, b):
    return (abs(a.q - b.q) 
          + abs(a.q + a.r - b.q - b.r)
          + abs(a.r - b.r)) / 2

Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи

расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе

. Например, описанная

здесь

«разность разностей» получается из записи

a.q + a. r - b.q - b.r

как

a.q - b.q + a.r - b.r

и с использованием формы максимального значения вместо формы деления пополам

cube_distance

. Все они аналогичны, если увидеть связь с кубическими координатами.

Координаты смещения

Как и в случае с осевыми координатами, мы

преобразуем

координаты смещения в кубические координаты, а затем используем расстояние кубической системы.

function offset_distance(a, b):
    var ac = offset_to_cube(a)
    var bc = offset_to_cube(b)
    return cube_distance(ac, bc)

Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).

Отрисовка линий

Как нарисовать линию от одного шестиугольника до другого? Я использую

линейную интерполяцию для рисования линий

. Линия равномерно сэмплируется в

N+1

точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.

GIF

1. Сначала мы вычисляем N, которое будет расстоянием в шестиугольниках между конечными точками.
2. Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N, включая их, каждая точка будет A + (B - A) * 1.0/N * i. На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
3. Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).

Соединяем всё вместе для отрисовки линии от A до B:

function lerp(a, b, t): // для float
    return a + (b - a) * t

function cube_lerp(a, b, t): // для шестиугольников
    return Cube(lerp(a.x, b.x, t), 
                lerp(a.y, b.y, t),
                lerp(a.z, b.z, t))

function cube_linedraw(a, b):
    var N = cube_distance(a, b)
    var results = []
    for each 0 ≤ i ≤ N:
        results. append(cube_round(cube_lerp(a, b, 1.0/N * i)))
    return results

Примечания:

• Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
• Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
• Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube. Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
• Можно оптимизировать код, встроив (inline) cube_lerp, а затем рассчитав B.x-A.x, B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
• Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите эту статью.
• Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие». Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.

Диапазон перемещения

Диапазон координат

Для заданного центра шестиугольника и диапазона

N

какие шестиугольники находятся в пределах

N

шагов от него?

Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)). Чтобы найти все шестиугольники в пределах N, нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N. Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N. Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N. В коде это будет вложенный цикл:

var results = []
for each -N ≤ dx ≤ N:
    for each -N ≤ dy ≤ N:
        for each -N ≤ dz ≤ N:
            if dx + dy + dz = 0:
                results.append(cube_add(center, Cube(dx, dy, dz)))

Этот цикл сработает, но будет довольно неэффективным. Из всех значений

dz

, которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов

dx + dy + dz = 0

. Вместо этого мы напрямую вычислим значение

dz

, удовлетворяющее условию:

var results = []
for each -N ≤ dx ≤ N:
    for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N):
        var dz = -dx-dy
        results. append(cube_add(center, Cube(dx, dy, dz)))

Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.

GIF

Пересекающиеся диапазоны

Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.

Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N, и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0, чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.

Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме xmin ≤ x ≤ xmax, и примем xmin = center.x - N и xmax = center.x + N. Сделаем то же самое для y и z, в результате получив общий вид кода из предыдущего раздела:

var results = []
for each xmin ≤ x ≤ xmax:
    for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin):
        var z = -x-y
        results.append(Cube(x, y, z))

Пересечением двух диапазонов

a ≤ x ≤ b

и

c ≤ x ≤ d

является

max(a, c) ≤ x ≤ min(b, d)

. Поскольку область шестиугольников выражена как диапазоны над

x

,

y

,

z

, мы можем отдельно пересечь каждый из диапазонов

x

,

y

,

z

, а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении.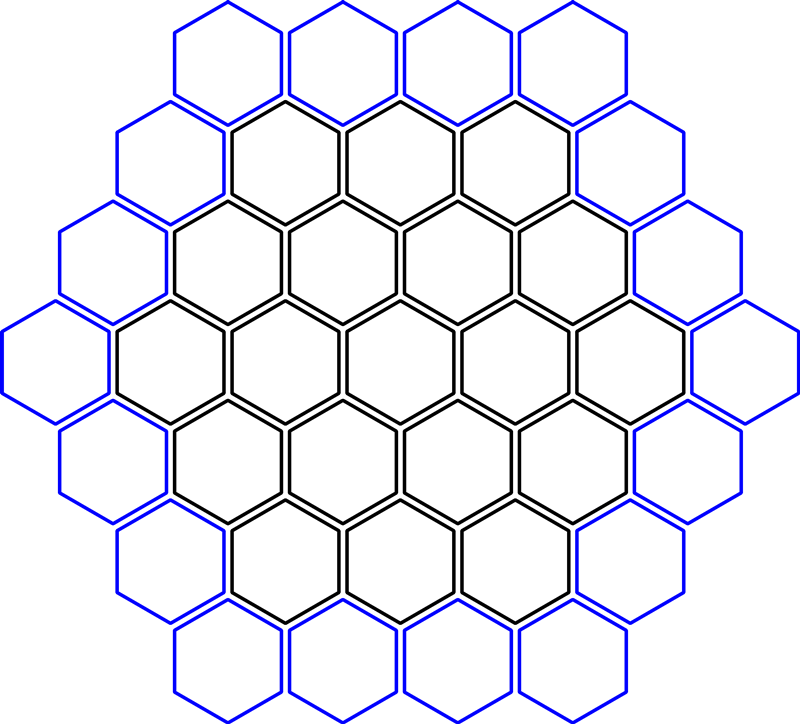 Для одной области шестиугольников мы принимаем

xmin = H.x - N

and

xmax = H.x + N

, аналогично для

y

и

z

. Для пересечения двух областей шестиугольников мы принимаем

xmin = max(h2.x - N, h3.x - N)

и

x

max = min(h2.x + N, h3.x + N), аналогично для

y

и

z

. Тот же шаблон работает для пересечения трёх или более областей.

GIF

Препятствия

При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде

fringes[k]

— это массив всех шестиугольников, которых можно достичь за

k

шагов. При каждом проходе по основному циклу мы расширяем уровень

k-1

на уровень

k

.

function cube_reachable(start, movement):
    var visited = set()
    add start to visited
    var fringes = []
    fringes. append([start])

    for each 1 < k ≤ movement:
        fringes.append([])
        for each cube in fringes[k-1]:
            for each 0 ≤ dir < 6:
                var neighbor = cube_neighbor(cube, dir)
                if neighbor not in visited, not blocked:
                    add neighbor to visited
                    fringes[k].append(neighbor)

    return visited

Повороты

Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.

Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:

        [ x,  y,  z]
to  [-z, -x, -y]

Поворот на 60° влево сдвигает каждую координату на одну позицию влево:

      [ x,  y,  z]
to        [-y, -z, -x]

«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60°

меняет

знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.

Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:

1. Преобразование положений P и C в кубические координаты.
2. Вычисление вектора вычитанием центра: P_from_C = P - C = Cube(P.x - C.x, P.y - C.y, P.z - C.z).
3. Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C.
4. Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z).
5. Преобразование кубического положения R обратно в нужную систему координат.

Здесь несколько этапов преобразований, но каждый из них довольно прост. Можно сократить некоторые из этих этапов, определив поворот непосредственно в осевых координатах, но векторы шестиугольников не работают с координатами смещения, и я не знаю, как сократить этапы для координат смещения. См. также

обсуждение

других способов вычисления поворота на stackexchange.

Кольца

Простое кольцо

Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса

radius

, нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно

radius

. Для получения списка всех таких шестиугольников нужно сделать

radius

шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.

function cube_ring(center, radius):
    var results = []
    # этот код не работает для radius == 0; вы понимаете, почему?
    var cube = cube_add(center, 
                        cube_scale(cube_direction(4), radius))
    for each 0 ≤ i < 6:
        for each 0 ≤ j < radius:
            results.append(cube)
            cube = cube_neighbor(cube, i)
    return results

В этом коде

cube

начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла

cube

двигается на один шестиугольник по кольцу. Через

6 * radius

шагов он завершает там, где начал.

Спиральные кольца

Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:

function cube_spiral(center, radius):
    var results = [center]
    for each 1 ≤ k ≤ radius:
        results = results + cube_ring(center, k)
    return results

Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра. Для вычисления площади используйте

эту формулу

.

Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).

Область видимости

Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.

Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.

GIF

Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд. Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.

В руководстве Кларка Вербрюгге описывается алгоритм для вычисления области видимости «начинаем с центра и двигаемся наружу». См. также проект Duelo, у которого есть на Github онлайн-демо области видимости с направлениями. Также можете прочитать мою статью об расчёте 2d-видимости, в ней есть алгоритм, работающий с многоугольниками, в том числе и с шестиугольниками. У сообщества любителей roguelike есть хороший набор алгоритмов для сеток квадратов (см. здесь, здесь и здесь). Некоторые из них можно адаптировать под сетки шестиугольников.

Шестиугольники в пиксели

Для перевода из шестиугольников в пиксели полезно изучить схему размеров и расположения, представленную в разделе «Геометрия». В случае осевых координат к преобразованию из шестиугольников в пиксели надо подходить, рассматривая базисные векторы. На схеме стрелка A→Q — это базисный вектор q, а A→R — базисный вектор r. Координата пикселя равна

q_basis * q + r_basis * r

. Например, B в (1, 1) является суммой базисных векторов q и r.

При наличии библиотеки матриц операция является простым умножением матриц. Однако здесь я запишу код без матриц. Для осевой сетки

x = q

,

z = r

, которую я использую в этом руководстве, преобразование будет иметь следующий вид:

Для шестиугольников с плоскими верхами

function hex_to_pixel(hex):
    x = size * 3/2 * hex.q
    y = size * sqrt(3) * (hex.r + hex.q/2)
    return Point(x, y)

Для шестиугольников с острыми верхами

function hex_to_pixel(hex):
    x = size * sqrt(3) * (hex.q + hex.r/2)
    y = size * 3/2 * hex.r
    return Point(x, y)

Матричный подход будет удобен позже, когда нам нужно будет преобразовать координаты пикселей обратно в координаты шестиугольников. Всё, что нам понадобится — обратить матрицу. Для кубических координат можно либо использовать кубические базисные векторы (x, y, z), или сначала преобразовать их в осевые, а затем использовать осевые базисные векторы (q, r).

Для координат смещения нам нужно будет сместить номер столбца или строки (он больше не будет целым). После этого можно использовать базисные векторы q и r, связанные с осями x и y:

Нечет-r

function offset_to_pixel(hex):
    x = size * sqrt(3) * (hex.col + 0.5 * (hex.row&1))
    y = size * 3/2 * hex.row
    return Point(x, y)

Чёт-r

function offset_to_pixel(hex):
    x = size * sqrt(3) * (hex.col - 0.5 * (hex.row&1))
    y = size * 3/2 * hex.row
    return Point(x, y)

Нечет-q

function offset_to_pixel(hex):
    x = size * 3/2 * hex.col
    y = size * sqrt(3) * (hex.row + 0.5 * (hex.col&1))
    return Point(x, y)

Чёт-q

function offset_to_pixel(hex):
    x = size * 3/2 * hex.col
    y = size * sqrt(3) * (hex.row - 0.5 * (hex.col&1))
    return Point(x, y)

К сожалению, координаты смещения не имеют базисных векторов, которые можно использовать вместе с матрицей. Это одна из причин того, почему преобразования из пикселей в шестиугольники сложнее в координатах смещения.

Другой подход: преобразовывать координаты смещения в кубические/осевые координаты, затем использовать преобразование кубических/осевых координат в пиксели. Благодаря встраиванию кода преобразования при оптимизации он в результате будет таким же, как выше.

Из пикселей в шестиугольники

Один из самых частых вопросов заключается в том, как взять положение пикселя (например, щелчка мыши) и преобразовать его в координату сетки шестиугольников? Я покажу, как это делается для осевых или кубических координат. Для координат смещения проще всего будет преобразовать в конце кубические координаты в координаты смещения.

GIF

1. Сначала мы инвертируем преобразование из шестиугольника в пиксели. Это даст нам дробные координаты шестиугольника, показанные на рисунке маленьким синим кругом.
2. Затем мы определим шестиугольник, содержащий дробную координату шестиугольника. Он показан на рисунке подсвеченным шестиугольником.

Для преобразования координат шестиугольников в координаты пикселей мы умножили

q

,

r

на базисные векторы для получения

x

,

y

. Можно считать это умножением матриц. Вот матрица для шестиугольников с острыми верхами:

Преобразование координат пикселей обратно в координаты шестиугольников достаточно прямолинейно. Мы можем обратить матрицу:

Эти вычисления дадут нам дробные осевые координаты (float) для

q

и

r

. Функция

hex_round()

преобразует дробные осевые координаты в целые осевые координаты шестиугольников.

Вот код для осевых шестиугольников с острыми верхами:

function pixel_to_hex(x, y):
    q = (x * sqrt(3)/3 - y / 3) / size
    r = y * 2/3 / size
    return hex_round(Hex(q, r))

А вот код для осевых шестиугольников с плоскими верхами:

function pixel_to_hex(x, y):
    q = x * 2/3 / size
    r = (-x / 3 + sqrt(3)/3 * y) / size
    return hex_round(Hex(q, r))

Эти три строчки кода преобразуют положение пикселя в осевую координату шестиугольника. Если вы используете координаты смещения, то воспользуйтесь

return cube_to_hex(cube_round(Cube(q, -q-r, r)))

.

Существует множество других способов преобразования пикселей в шестиугольники. На этой странице перечислены известные мне.

Округление до ближайшего шестиугольника

Иногда у нас получается кубическая координата (x, y, z)

с плавающей запятой

, и нам нужно узнать, в каком шестиугольнике она должна находиться. Это выясняется отрисовкой линии и преобразованием из пикселей в шестиугольники. Преобразование значения с плавающей запятой в целое значение называется

округлением

(rounding), поэтому я назвал этот алгоритм

cube_round

.

В кубических координатах x + y + z = 0 даже при кубических координатах с плавающей точкой. Поэтому давайте округлим каждую компоненту до ближайшего целого (rx, ry, rz). Однако, хотя x + y + z = 0, после округления у нас нет гарантий того, что rx + ry + rz = 0. Поэтому мы изменяем компоненту с самым большим изменением так, чтобы условие rx + ry + rz = 0 было верным. Например, если изменение y abs(ry-y) больше abs(rx-x) и abs(rz-z), то мы изменяем его на ry = -rx-rz. Это гарантирует нам, что rx + ry + rz = 0. Вот алгоритм:

function cube_round(h):
    var rx = round(h.x)
    var ry = round(h.y)
    var rz = round(h.z)

    var x_diff = abs(rx - h.x)
    var y_diff = abs(ry - h.y)
    var z_diff = abs(rz - h.z)

    if x_diff > y_diff and x_diff > z_diff:
        rx = -ry-rz
    else if y_diff > z_diff:
        ry = -rx-rz
    else:
        rz = -rx-ry

    return Cube(rx, ry, rz)

Для некубических координат проще всего будет преобразовать их в кубические координаты, воспользоваться алгоритмом округления, а затем преобразовать обратно:

function hex_round(h):
    return cube_to_hex(cube_round(hex_to_cube(h)))

Примечание о реализации:

cube_round

и

hex_round

получают координаты в float, а не в int. Если вы написали классы

Cube

и

Hex

, они будут отлично работать в языках с динамической типизацией, в которых можно передавать числа с плавающей запятой вместо целых, и в языках со статической типизацией с унифицированным типом чисел. Однако в большинстве языков со статической типизацией нужен будет отдельный тип class/struct для координат float и

cube_round

будет иметь тип

FloatCube → Cube

. Если вам также нужна

hex_round

, она будет

FloatHex → Hex

, использующей вспомогательную функцию

floatcube_to_floathex

вместо

cube_to_hex

. В языках с параметризированными типами (C++, Haskell и т.д.) можно определить Cube, где T является int или float. Или же можно написать

cube_round

для получения трёх чисел с плавающей точкой в качестве входных данных вместо определения нового типа только для этой функции.

Хранение карт в осевых координатах

Чаще всего осевая система координат вызывает жалобы потому, что приводит к ненужному расходованию пространства при использовании прямоугольных карт. Это одна из причин в пользу системы координат смещения. Однако все системы координат шестиугольников приводят к расходу пространства при использовании треугольных или шестиугольных карт. Мы можем использовать одну стратегию для хранения всех этих типов карт.

Прямоугольная карта

Треугольная карта

Шестиугольная карта

Ромбовидная карта

Заметьте на схеме, что неиспользуемое пространство находится справа и слева от каждой строки (за исключением ромбовидных карт). Это даёт нам три варианта стратегий хранения карты:

1. Игнорировать проблему. Использовать сплошной массив с нулями или другими индикаторами неиспользуемого пространства. Для этих стандартных форм карт неиспользуемое пространство может занимать максимум половину массива. Возможно, использование более сложных решений нерационально.
2. Использовать вместо сплошного массива хеш-таблицу. Это позволяет использовать карты произвольной формы, в том числе и с отверстиями. Когда нужно получить доступ к шестиугольнику в q,r мы вместо этого получаем доступ к hash_table(hash(q,r)). Инкапсулируем её в геттер/сеттер в классе сетки, чтобы остальная часть игры не должна была знать о ней.
3. Сместить строки влево и использовать строки с переменным размером. Во многих языках двухмерный массив является массивом массивов. Массивы необязательно должны быть одной длины. Это позволяет избавиться от неиспользуемого пространства справа. Кроме того, если начинать массивы с самого левого столбца вместо 0, то удалится неиспользуемое пространство слева.

   Чтобы применить эту стратегию в произвольных выпуклых картах, необходимо хранить дополнительный массив «первых столбцов». Когда нужно получить доступ к шестиугольнику в q,r, мы вместо этого получаем доступ к array[r][q - first_column[r]]. Инкапсулируем его в геттер/сеттер в классе сетки, чтобы остальная часть игры не должна была знать о нём. На съеме first_column показан в левой части каждой строки.

   Если карты имеют фиксированные формы, то «первые столбцы» можно вычислять «на лету», а не хранить их в массиве.

   • Для прямоугольных карт first_column[r] == -floor(r/2). В результате мы получаем доступ к array[r][q + r/2], что оказывается аналогом преобразования координат в координаты смещения сетки.
   • Для треугольных карт, как здесь показано, first_column[r] == 0, поэтому мы получаем доступ к access array[r][q] — очень удобно! Для треугольных карт, ориентированных по-другому (не показаны на схеме), это будет array[r][q+r].
   • Для шестиугольных карт радиуса N, где N = max(abs(x), abs(y), abs(z), у нас получается first_column[r] == -N - min(0, r). Мы получаем доступ к array[r][q + N + min(0, r)]. Однако так как мы начинаем с каких-то значений r < 0, нам также нужно сместить строку и использовать array[r + N][q + N + min(0, r)].
   • Для ромбовидных карт всё идеально совпадает, поэтому можно использовать массив array[r][q].

Зацикленные карты

В некоторых играх требуется, чтобы карта «склеивалась» по краям. Квадратную карту можно обернуть только по оси x (что примерно соответствует сфере) или по обеим осям x и y (что примерно соответствует тору). Сворачивание зависит от формы карты, а не от формы её элементов. Сворачивание квадратной карты проще выполняется в координатах смещения. Я покажу, как выполняется сворачивание шестиугольной карты в кубических координатах.

Относительно центра карты существует шесть «зеркальных» центров. При выходе с карты мы вычитаем ближайший к нам зеркальный центр, пока снова не вернёмся на основную карту. На схеме [в оригинале статьи] попробуйте покинуть центральную карту, и понаблюдайте, как один из зеркальных центров входит в карту с противоположной стороны.

Простейшей реализацией будет предварительное вычисление ответов. Создаём таблицу подстановок, хранящую для каждого шестиугольника, выходящего с карты, соответствующий куб с другой стороны. Для каждого из шести зеркальных центров M и для каждого из положений на карте L храним mirror_table[cube_add(M, L)] = L. Каждый раз при вычислении шестиугольника, находящегося в таблице зеркал заменяем его неотзеркаленной версией.

На шестиугольной карте с радиусом N зеркальные центры будут Cube(2*N+1, -N, -N-1) и шестью его поворотами.

GIF

Поиск пути

При использовании поиска пути на графах, например алгоритма поиска A*, алгоритма Дейкстры или Флойда-Уоршелла поиск пути на сетках шестиугольников не отличается от поиска пути на сетках квадратов. Пояснения и код из моего

руководства по поиску пути

применимы и для сеток шестиугольников.

[В оригинале статьи пример интерактивен, нажатиями мыши можно добавлять и удалять стены]

1. Соседи. Пример кода, представленный в руководстве по поиску пути, вызывает для получения соседних с положением элементов graph.neighbors. Используйте для этого функцию в разделе «Соседние шестиугольники». Отфильтровывайте непроходимые соседние шестиугольники.
2. Heuristic. В примере кода алгоритма A* используется функция heuristic, получающая расстояние между двумя положениями. Используйте формулу расстояний, умноженную на затраты на передвижение. Например, если перемещение стоит 5 единиц на шестиугольник, то умножайте расстояние на 5.

Дополнительное чтение

У меня есть

руководство по реализации собственной библиотеки сеток шестиугольников

с примерами кода на C++, Java, C#, Javascript, Haxe и Python.

• В моём руководстве по сеткам я рассматриваю осевые системы координат и обработку граней и углов квадратов, треугольников и шестиугольников. Также я объясняю, как связаны сетки квадратов и шестиугольников.
• Лучшим ранним руководством, которое я видел, стало руководство Кларка Вербрюгге, написанное в 1996 году.
• Впервые я увидел кубическую систему координат в посте 1994 года Чарльза Фу в rec.games.programmer.
• В DevMag есть хороший визуальный обзор математики шестиугольников, включая способы представления площадей, таких как полуплоскости, треугольники и четырёхугольники. Существует версия в PDF, которая немного подробнее. Крайне рекомендуется к изучению! Библиотека GameLogic Grids реализует эти и многие другие типы сеток в Unity.
• У Джеймса Макнейла есть хорошее визуальное объяснение преобразований сеток.
• Обзор типов координат шестиугольников: ступенчатых (со смещением), чередуемых, трёхмерных (кубических) и трапецеидальных (осевых).
• Библиотека Rot.js содержит список систем координат шестиугольников: неортогональной (осевой), с нечётным сдвигом (со смещением), двойной ширины (чередуемой), кубической.
• Диапазон в кубических координатах: какие шестиугольники находятся на заданном расстоянии от заданного?
• Определение расстояний в сетках шестиугольников с помощью кубических координат и объяснение причин использования кубических координат вместо координат смещения.
• В этом руководстве объясняются основы измерения и отрисовки шестиугольников с помощью сетки смещения.
• Преобразование кубических координат шестиугольников в координаты пикселей.
• В этом посте объясняется, как генерировать кольца.
• В системе HexPart используются как шестиугольники, так и прямоугольники для упрощения работы с некоторыми алгоритмами.
• Есть ли плюсы и минусы у шестиугольников с плоским и острым верхом?
• Линия видимости в сетке шестиугольников с координатами смещения, разделение шестиугольников на треугольники. [Нерабочая ссылка]
• Hexnet объясняет, что соотношение между шестиугольниками и кубами намного глубже, чем я описал в этой статье, и обобщает связь до большего количества измерений.
• Я использовал PDF с сетками шестиугольников с этой страницы, когда работал над некоторыми алгоритмами.
• Обобщённая сбалансированная троичная система счисления для координат шестиугольников выглядит интересно; я пока не изучал её.
• Hex-Grid Utilities — это библиотека C# с открытым исходным кодом для математики сеток шестиугольников с определением соседних шестиугольников, сетками, поиском диапазонов и путей, областью видимости. Лицензия MIT.
• В обсуждениях на Reddit, Hacker News и MetaFilter есть больше комментариев и ссылок.

Код [оригинала] этой статьи написан на смеси

Haxe

и Javascript:

Cube.hx

,

Hex.hx

,

Grid.hx

,

ScreenCoordinate.hx

,

ui.js

и

cubegrid.js

(для анимации кубов/шестиугольников). Однако если вы хотите написать свою библиотеку сеток шестиугольников, то рекомендую вместо этого кода изучить

моё руководство по реализации

.

Я хочу в дальнейшем расширять это руководство. У меня есть список на Trello.

Как нарисовать правильный 6 угольник. Правильный шестиугольник и его свойства. Последние штрихи и узор

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°.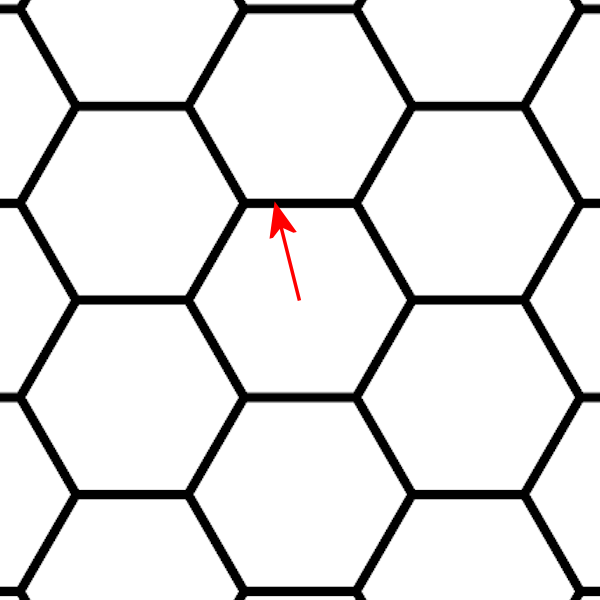 Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°.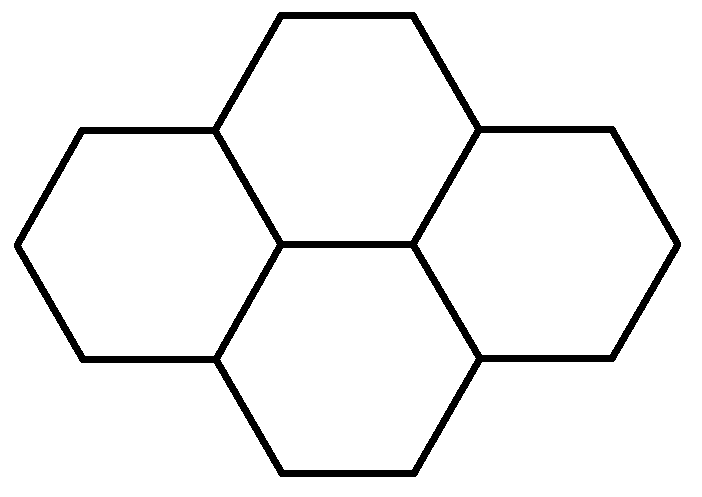 Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2 .

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4 ,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а , или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

S=3(2r/√3)²(√3)/2=r²(2√3)

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .

Рисунок 38

Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.

Рисунок 39

Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.

Рисунок 40

Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.

Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:

• Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.

Научимся изображать шестигранную призму в различных положениях.

Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.

На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.

Горизонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.

На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.

Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).

Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.

Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).

Архив Галактики

Геометрия и карандашное программирование

Блог тренера / 05.07.2016

Как учителю математики мне интересны те возможности, которые позволят опираться на геометрические понятия и использовать фигуры геометрии в качестве объектов для карандашного программирования, для рисования кодом в pencilcode. Только здесь привычные инструменты, такие, как линейка и циркуль, заменяются блочными операторами.
Кроме того, поскольку некоторое время назад увлеклась темой “переплетения” учебных предметов математики и искусства, нашла в этом новом для меня инструменте новые возможности для таких проектов. Таким образом получится “переплести” уже три разных школьных предмета, добавив к двум первым еще и информатику.

1. Рисование правильных многоугольников

Хорошо начать изучение “карандашной” программы с линейных алгоритмов и построить с помощью простых команд вперед-назад, влево-вправо геометрические фигуры с заданными линейными размерами и углами: квадрат, ромб, трапецию и т.д.. Отдельным комплексным заданием может быть практикум по созданию правильных многоугольников.

Квадрат

Треугольник
Пятиугольник

При создании пятиугольника понадобится вычислить угол поворота черепашки влево (или вправо). Для этого пригодится знание формулы суммы углов в правильном N-угольнике, расчет величины угла и понятие смежных углов.
Для закрепления темы хорошо также создать с помощью черепашки другие правильные многоугольники с целыми внутренними углами, по дороге выяснив, какие из них вы сможете построить таким “карандашом”.

2. Правильные многоугольники. Переход к циклам.

Для того, чтобы переход от первой темы был плавным, можно предложить ученикам оптимизировать (упростить, укоротить) код, использовавшийся в первом задании для построения правильных фигур. Тело цикла будет состоять из двух команд — движение вперед и поворот на один и тот же угол). Покажем на примере построения правильного шестиугольника.

Шестиугольник

Затем учащиеся оптимизируют с использованием блока “цикл” прежние свои построения правильных многоугольников, изменяя в них количество шагов и угол поворота черепашки.
Что нарисовать?

Задачи-вызовы
Предложите ученикам нарисовать с помощью циклов комбинации правильных многоугольников и, например, черепашек

Комбинация правильных треугольников
Черепашка

Или такие фигуры из правильных шестиугольников.

Соты
Поликуб

3. Квадратный узор. Вложенные циклы.

Все описанные в этом блоке образцы создаются на основе квадратной сетки и простых команд движения черепашки. Из понятий информатики используются циклы и вложенные циклы.

Рисуем окошко

Еще несколько задач-узоров для записи кода учениками. Можно предложить ученикам по этому принципу придумать и свои узоры.

Рисунок 1
Рисунок 2
Рисунок 3
Рисунок 4

4. Решетки на основе правильных многоугольников.

Решетки на основе квадрата

Здесь используются вложенные циклы и это хорошее упражнение на построение разных типов решеток: на основе правильного треугольника, квадрата, пяти- и шестиугольника. В качестве базового можно дать решетку на основе квадрата и предложить ученикам изменить ее в другие типы решеток.

Эффект спирографа
Использовав базовый образец и меняя в нем параметры, можно получить красивые фигуры. Отдельный разговор может состояться о количестве шагов в цикле и его связи с другими параметрами — углами поворота и длинами сторон фигуры.

Фигура 1

6. Рисование дугами

Эту тему тоже хорошо дать в виде индивидуальных проектов. Причем, можно не тратить время на теоретическое изучение команд, а предложить ученикам разобраться с этим простым шаблоном и на его основе создать свой узор дугами. Выкладываю с кодом

Розетка с 6 лепестками

Витраж 1
Витраж 2
Витраж 3

Может, кто-то из читателей попробует что-то создать?
Что рисовать? Вот примеры шаблонов:

Шаблоны для индивидуальных проектов можно найти, рассматривая витражи готических соборов. Для готики характерны многоцветные витражные окна:

В заключение немного современных принтов:
Flower Extract Art Print by Akamundo Рисунок в посте STEAM-проект: задачи на картинах

Результат в pencilcode: Akamundo
Честно говоря, за решение подобной задачи можно смело ставить пятерку по геометрии (в тему углы и окружности).

Полезные ссылки
Видео. Рисование правильных многоугольников, поворот на угол, рисование дуг в pencilcode
Рисование линий в pencilcode

Идей для «рисования» геометрических фигур с помощью «карандаша» может быть очень много. Они находятся, в том числе, и по этому списку ссылок:
Ссылки по теме:
Оригинальный материал: Geometric Design: The Basics
Перевод на русский язык:
Геометрия как искусство (инструменты)
Геометрия как искусство (часть вторая)
Геометрия как искусство: 4 и 8 (часть третья)

Идеи для выполнения проектов в Pencilcode
STEAM-проект: задачи на картинах
Идеи в духе STEAM: геометрический конструктор на основе рисунков Google

Посты по теме *Появляются по мере публикации
Карандашное программирование. Начало
Карандашное программирование: смайломания
Карандашное программирование: чужой код для решения своей задачи…
Карандашное программирование: циклы
Геометрия и карандашное программирование
Карандашное программирование: холст как координатная плоскость
Карандашное программирование: рисуем пейзажи масштабированием
Карандашное программирование: четыре черепашки и симметричный дизайн
Карандашное программирование: несколько черепашек и поворотная симметрия
Карандашное программирование: черепашка рисует паркеты и мозаики
Карандашное программирование: черепашка и оптические иллюзии
О творческих домашних заданиях, или Могут ли все ученики быть успешными?
Программирование для воссоздания картин: математика и искусство вместе
В начале была цифра?
Пляшущие черепашки
Искусство создания снежинки, или Как скоротать зиму. ..
Карандашное программирование: паркеты и жывёлы
Карандашное программирование: рекурсия
Ёлка в коде. МК
Ёлка в коде. Этап 2. Шарики цветные
Прекрасная геометрия на бумаге и не только…

STEAM

pencilcode

блочное программирование

искусство

математика

программирование

проект

симметрия

Что насчет пчел и шестиугольников? : Чудеса Крулвича … : NPR

Решено! Жужжащая пчела, лизающая мед 2000-летняя загадка, которая начинается здесь, с этого улья. Посмотрите на соты на фото и спросите себя: (Я знаю, вы всю жизнь задавались этим вопросом, но стеснялись спросить вслух…) Почему каждая ячейка в этих сотах представляет собой шестиугольник?

В конце концов, пчелы могут строить соты из прямоугольников, квадратов или треугольников. ..

Но почему-то пчелы выбирают шестиугольники. Всегда шестиугольников.

И не только шестиугольник. Им нравятся «идеальные» шестиугольники, то есть все шесть сторон равны и имеют одинаковую длину. Они выбирают ювелирную версию — точную, именно так. Почему?

Ну, это очень старый вопрос. Более 2000 лет назад, в 36 г. до н.э., римский солдат, ученый и писатель Марк Теренций Варрон предложил ответ, который с тех пор называется «гипотезой медоносной пчелы».» Варрон подумал, что может быть глубокая причина такого поведения пчел. Может быть, соты, построенные из шестиугольников, могут вместить больше меда. Может быть, шестиугольники требуют меньше строительного воска. Может быть, здесь есть скрытая логика.

, хаос повседневной жизни, могут быть элегантные причины того, что мы видим. «Гипотеза медоносной пчелы» является примером математики, раскрывающей тайну природы, поэтому здесь, с помощью физика/писателя Алана Лайтмана (который недавно написал об этом в журнале Orion) — это догадка Варрона.

Основные соты

Мы все знаем, что в сотах хранится мед. Мед, безусловно, ценен для пчел. Кормит их детенышей. Он поддерживает улей. Это делает воск, который скрепляет соты. Требуются тысячи и тысячи пчело-часов, десятки тысяч полетов по лугу, чтобы собрать нектар с цветка за цветком и за цветком, поэтому разумно предположить, что в улье пчелам нужна плотная, надежная структура для хранения, максимально просто построить.

Итак, как его построить? Ну, предположим, вы начинаете свои соты с такой ячейки… совершенно случайной формы, без равных сторон, просто загогулина…

Если вы начнете таким образом, как будет выглядеть ваша следующая ячейка? Ну, вам не нужны большие промежутки между ячейками. Вы хотите, чтобы структура была плотной. Так что следующую ячейку придется настраивать, чтобы цеплялась за первую, вот так…

И опять же, третья камера должна быть спроектирована так, чтобы соответствовать первым двум. Каждая ячейка будет немного отличаться, а это значит, говорит Алан Лайтман…

… такой метод построения сот потребует, чтобы рабочие пчелы работали последовательно, по одной, сначала делая одну ячейку, затем подгонка следующей ячейки к этой и так далее.

Но это не лучший путь. «Посмотрите на любую версию YouTube о пчелах, строящих соты, — говорит Алан, — и вы не увидите множества пчел, слоняющихся без дела в ожидании своей очереди, чтобы построить соту».Вместо этого все работают. Они делают это коллективно, одновременно и постоянно.

Таким образом, план с волнистыми ячейками создает праздных пчел. Это пустая трата времени. Чтобы пчелы собирали соты так, как это делают пчелы на самом деле, проще, чтобы каждая ячейка была абсолютно одинаковой. Если все стороны равны — «идеально» шестиугольные — каждая ячейка плотно прилегает к каждой другой ячейке. Каждый может принять участие. Таким образом, соты — это, по сути, простая головоломка. Все детали подходят.

Хорошо, это объясняет, почему сотовые ячейки имеют одинаковый размер.Но вернемся к нашему первому вопросу: почему предпочтение отдается шестиугольникам? Есть ли что-то особенное в шестигранной форме?

Некоторые фигуры, о которых вы сразу узнаете, не очень хороши. Соты, построенные из сфер, будут иметь небольшие промежутки между каждым элементом …

… создание зазоров, для заполнения которых потребуется дополнительный воск. Итак, вы понимаете, почему соты, построенные из сфер, не были бы идеальными. Пятиугольники, восьмиугольники также производят зазоры. Что лучше?

«Это математическая истина, — пишет Лайтман, — что есть только три геометрические фигуры с равными сторонами, которые могут совмещаться на плоской поверхности, не оставляя зазоров: равносторонние треугольники, квадраты и шестиугольники.»

Так что же выбрать? Треугольник? Квадрат? Или шестигранник? Какой из них лучше? Вот где наш римлянин Марк Теренций Варрон внес свой большой вклад. Его «гипотеза» — а это была математическая догадка — предполагала, что структура, построенная из шестиугольников, вероятно, немного компактнее, чем структура, построенная из квадратов или треугольников. Он думал, что шестиугольные соты будут иметь «наименьший общий периметр». Он не мог доказать это математически, но он так думал.

Компактность имеет значение. Чем компактнее ваша структура, тем меньше воска вам потребуется для создания сот. Воск дорогой. Пчела должна потреблять около восьми унций меда, чтобы произвести одну унцию воска. Поэтому, если вы следите за своим счетом за воск, вам нужен самый компактный план здания, который вы можете найти.

И знаете что?

[Соты] абсолютно идеальны в плане экономии труда и воска.

Чарльз Дарвин

Через две тысячи тридцать пять лет после того, как Маркус Теренций Варрон выдвинул свою гипотезу, математик из Мичиганского университета Томас Хейлз разгадал загадку.Оказывается, Варрон был прав. Шестиугольная структура действительно компактнее. В 1999 году Хейлз представил математическое доказательство, подтверждающее это.

Как подозревали древние греки, как утверждал Варрон, как всегда думали любители пчел, как когда-то писал сам Чарльз Дарвин, соты — это шедевр инженерного искусства. Он «абсолютно идеален в плане экономии труда и воска».

Пчелы, надо полагать, пожали плечами. Как говорит Алан Лайтман: «Они всегда знали, что это правда».

Эссе Алана Лайтмана «Симметричная Вселенная», первоначально опубликованное в журнале Orion Magazine, будет включено в его новую книгу Случайная Вселенная: Мир, который, как вы думали, вы знали , который будет опубликован в начале следующего года.Я также рекомендую эссе Иварса Петерсона в журнале Science News, The Honeycomb Conjecture.

кодов для рисования сот · GitHub

кодов для рисования сот · GitHub

Мгновенно делитесь кодом, заметками и фрагментами.

коды для рисования сот

Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже.Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode

	импортировать java.awt.*
	класс Утилиты {
	определение getGoodRenderingHints () {
	def hints = новые RenderingHints(RenderingHints. KEY_ANTIALIASING,RenderingHints.VALUE_ANTIALIAS_ON)
	hints.put(RenderingHints.KEY_RENDERING, RenderingHints.VALUE_RENDER_QUALITY)
	подсказки
	}
	по умолчанию outputAsPNG (по умолчанию bimg, по умолчанию вне файла) {
	def out = новый FileOutputStream(outfile)
	новый javax.imageio.ImageIO().write(bimg,»png»,out)
	выход.закрыть()
	}
	по определению createImage(Размер размера){
	новый java. awt.image.BufferedImage((int)size.width,(int)size.height,java.awt.image.BufferedImage.TYPE_4BYTE_ABGR)
	}
	}
	абстрактный класс AbstractHoneycombDiagram {
	размер по умолчанию
	защитный внешний файл
	def AbstractHoneycombDiagram (размер размера, def outfile) {
	это. размер = размер
	этот.выходящий файл = исходящий файл
	}
	определение прямоугольника (ячейка определения) {
	def cu = новый org.notehub.ntwo.painter.TextBoxLocationCalcUtil2 (ячейка)
	def padding = новые вставки (-2,5,-2,5)
	по умолчанию = орг.notehub.ntwo.painter.TextBoxLocationCalcUtil2.padding(cu.rectangle, padding)
	прямоугольный
	}
	по определению paintTextArea (по определению g2, по ячейке) {
	g2. fill( toRectangle(cell))
	}
	определение paintText (определение g2, определение ячейки, определение текста) {
	def tp = новая орг.notehub.awt.painter.TextPainter(текст)
	tp.verticalAlignment = org.notehub.awt.painter.TextPainter.MIDDLE
	tp.horizontalAlignment = org.notehub.awt.painter.TextPainter.CENTER
	def rect = toRectangle (ячейка)
	tp. location = new Point( (int)rect.х, (целое)прямо.у )
	tp.size = новый размер ((int)rect.width, (int)rect.height)
	тп.краска(г2)
	}
	абстрактное определение createHoneycomb()
	дефгенерировать(){
	def u = новые утилиты ()
	// 1)
	по определению bimg = u. создатьИзображение (размер)
	по умолчанию g2 = bimg.graphics
	g2.renderingHints = u.goodRenderingHints
	// 2)
	g2.color = Цвет.БЕЛЫЙ
	g2.fill( новый прямоугольник(0,0,(int)size.width,(int)size.высота) )
	// 3)
	//def h = новый org.notehub.ntwo.painter.HoneycombOne()
	определение ч = создать соты ()
	h. size = org.notehub.ntwo.painter.DrawingUtils.toXDimension(this.size)
	час.getHexagonShapes().eachWithIndex{ форма, индекс->
	// 3-1) бордюр
	g2.color = Цвет.ЧЕРНЫЙ
	g2.draw(форма)
	// 3-2) закрасить текстовую область
	г2.цвет = новый цвет (0xEE, 0xEE, 0xEE)
	paintTextArea(g2, shape.hexagonCell)
	// 3-3) нарисуйте текст
	g2. color = Цвет.ЧЕРНЫЙ
	paintText( g2, shape.hexagonCell, «${index}) Привет» )
	}
	г2.распоряжаться ()
	u.outputAsPNG (бимг, выходной файл)
	}
	}
	класс HoneycombDiagramOne расширяет AbstractHoneycombDiagram{
	def HoneycombDiagramOne (размер размера, def outfile) {
	супер(размер,выходной файл)
	}
	деф createHoneycomb(){
	новая орг. notehub.ntwo.painter.HoneycombOne()
	}
	}
	класс HoneycombDiagramTwo расширяет AbstractHoneycombDiagram{
	def HoneycombDiagramTwo (размер размера, def outfile) {
	супер(размер,выходной файл)
	}
	деф createHoneycomb(){
	новая орг.notehub.ntwo.painter.HoneycombTwo()
	}
	}
	x = новый HoneycombDiagramOne (новое измерение (300 300), новый файл (‘one. png’))
	x.генерировать()
	x = new HoneycombDiagramTwo (новое измерение (720 600), новый файл (‘two.png’)) )
	x.генерировать()

Вы не можете выполнить это действие в данный момент. Вы вошли в другую вкладку или окно. Перезагрузите, чтобы обновить сеанс. Вы вышли на другой вкладке или в другом окне. Перезагрузите, чтобы обновить сеанс.

Создание бесшовного сотового рисунка в Photoshop

Обновлено в августе 2017 г. для Adobe Photoshop CC.

Есть много способов сделать бесшовный узор в виде сот в Photoshop, и сегодня я покажу вам свою любимую технику. Как только вы поймете метод, используемый в этом уроке, вы сможете экспериментировать с разными размерами и даже другими формами, такими как треугольники.

Посмотреть обучающее видео на YouTube

Недавно я открыл новый канал на YouTube, на котором я покажу вам, как использовать Photoshop и Illustrator для создания бесшовных узоров и графики для вашего блога, бизнеса или социальных сетей.Пожалуйста, подпишитесь на канал Elan Creative Co, если хотите видеть больше видеоуроков.

Я новичок в этом деле и очень нервничаю, так что извините за мои ошибки ?

Вот как сделать бесшовный узор в виде сот в Photoshop. Прокрутите вниз для письменного учебника.

Как сделать бесшовный сотовый узор в Photoshop

Для начала откройте новый документ и выберите нужный размер и разрешение. Я использую холст размером 800 x 800 пикселей с плотностью 72 ppi. Я собираюсь начать с прозрачного фона, но вы также можете использовать белый фон и удалить его позже. Я использую прозрачный фон, потому что хочу иметь возможность перекрашивать рисунок.

Установите цвет переднего плана на черный или ваш любимый цвет и создайте шестиугольник с помощью инструмента Polygon Tool . Убедитесь, что Стороны установлены на 6.

Создайте два новых шестиугольника, дублируя исходный многоугольник и выровняв их с первым шестиугольником. Оставьте зазор между ними.Вы можете оставить столько места, сколько хотите, просто убедитесь, что промежутки одинакового размера.

Совет: Включите Smart Guides , выбрав View > Show > Smart Guides . Это поможет вам выровнять фигуры.

Дублируйте первые два слоя и поместите их поверх первых трех шестиугольников.

Дублируйте два шестиугольника сверху и переместите их под три шестиугольника.

Вот как будут выглядеть ваши соты:

С помощью Move Tool выберите три шестиугольника, которые находятся посередине, и слегка переместите их вверх и вниз, влево и вправо, пока они не будут отцентрированы. Розовые интеллектуальные направляющие появятся на экране, когда они будут центрированы.

Теперь, когда у нас есть соты из семи шестиугольников, нам нужно их обрезать. Чтобы помочь вам сделать это, включите линейки из View > Rulers (Ctrl + R). Также убедитесь, что установлен флажок View > Snap (Ctrl + Shift + ; ).

Вам нужно будет добавить две горизонтальные линейки и две вертикальные линейки.

Выберите шестиугольник слева от верхнего ряда (номер 1 на изображении).Нажмите на верхнюю линейку и перетащите направляющую, пока она не достигнет середины шестиугольника. Вы почувствуете, как он встанет на место, когда он окажется посередине.

Сделайте то же самое для шестиугольника номер 2.

Выберите шестиугольник с номером 3 на изображении выше и перетащите вертикальную направляющую с линейки слева. Вы почувствуете, как он встанет на место, когда он окажется в центре шестиугольника.

Сделайте то же самое для шестиугольника номер 4.

Теперь мы обрежем сотовый узор.Используйте инструмент Crop Tool , чтобы выбрать область внутри направляющих.

Нажмите кнопку проверки в правом верхнем углу экрана, чтобы сохранить изменения.

Чтобы сохранить бесшовный сотовый узор, выберите Правка > Определить узор .

Как сделать шестиугольный фон

Мы собираемся использовать бесшовный шестиугольный узор и создать фон для вашей графики.

Создайте новый холст и выберите нужный размер.Используя Fill Tool , перекрасьте фоновый слой.

Создайте новый слой и перейдите к Edit > Fill и выберите сотовый узор из выпадающего списка.

Давайте изменим цвет сотового рисунка. Создайте новый слой поверх слоя с узором и измените его цвет с помощью инструмента «Заливка» .

Используйте обтравочную маску, чтобы изменить цвет шестиугольника. Убедитесь, что выбран слой сплошного цвета, и перейдите в Слой > Создать обтравочную маску (Alt + Ctrl + D).

Если вы хотите раскрасить только несколько шестиугольников, как я сделал на показанном изображении, вы можете сделать это с помощью инструмента «Заливка» и щелкнуть каждый шестиугольник, который вы хотите перекрасить. Убедитесь, что вы делаете это на исходном фоне шестиугольника, а обтравочная маска скрыта.

Вот и все! Теперь у вас есть сотовый узор, который вы можете использовать в качестве фона для своего веб-сайта или в своих проектах.

Было ли это руководство полезным? Узнайте, как сделать больше бесшовных узоров здесь.

Ведущие компании Avion Alloys, AirMetals, Southern Tool Steel, Coast-Line International – Cleveland Sports Zone

Глобальная индустрия гибких сот: значительный среднегодовой рост в течение 2022–2027 годов

Новый исследовательский отчет о рынке гибких сот, который охватывает обзор рынка, будущее экономическое воздействие, конкуренцию производителей, анализ предложения (производства) и потребления

Узнайте о влиянии COVID-19 на рынок гибких сот с нашими аналитиками, отслеживающими ситуацию по всему миру. Запросить сейчас

Отчет об исследовании рынка глобальной отрасли гибких сот обеспечивает всестороннее исследование различных технологий и материалов, используемых при производстве рыночных продуктов гибких сот. Начиная с анализа отраслевой цепочки и заканчивая анализом структуры затрат, отчет анализирует множество аспектов, включая сегменты производства и конечного использования рыночных продуктов Гибкие соты. В отчете подробно описаны последние тенденции в фармацевтической промышленности, чтобы оценить их влияние на производство рыночных продуктов «Гибкие соты».

С раскрытием нынешних рыночных стандартов отчет об исследовании рынка гибких сот также непредвзято иллюстрирует последние стратегические разработки и модели участников рынка. Отчет служит предполагаемым деловым документом, который может помочь покупателям на мировом рынке спланировать свой следующий курс в отношении положения рынка в будущем.

Получить образец этого отчета @ https://www. marketresearchupdate.com/sample/361763

Ведущими ключевыми игроками на рынке гибких сот являются –
Avion Alloys, AirMetals, Southern Tool Steel, Coast-Line International, Prime Laminating, ThomasNet, The Gill Corp, Pacific Marine System

Типы изделий:
Металл
Пластик

На основании применения:
Химическая промышленность
Энергетика

Региональный анализ рынка гибких сот

Северная Америка  (США, Канада и Мексика)
Европа  (Германия, Франция, Великобритания, Россия и Италия)
Азиатско-Тихоокеанский регион , Корея (Китай, Корея, Индия и Юго-Восточная Азия)
Южная Америка (Бразилия, Аргентина, Колумбия и т. д.)
Ближний Восток и Африка (Саудовская Аравия, ОАЭ, Египет, Нигерия и Южная Африка)

Получите скидку на отчет Flexible Honeycomb @ https://www. marketresearchupdate.com/discount/361763

• В этом отчете описаны различные сценарии развития рынка в целом и представлена ​​дорожная карта того, как продукты Flexible Honeycomb заняли свое место на этом быстро меняющемся рынке. Участники отрасли могут изменить свои стратегии и подходы, изучив прогноз размера рынка, упомянутый в этом отчете.Были выявлены прибыльные торговые площадки для рынка гибких сот, которые могут повлиять на стратегии глобального расширения ведущих организаций. Тем не менее, каждый производитель был подробно описан в этом исследовательском отчете.
В главе «Анализ факторов влияния на рынок гибких сот»
• особое внимание уделяется технологическому прогрессу / риску, угрозе замещения, потребительским потребностям / изменениям предпочтений клиентов, технологическому прогрессу в смежной отрасли и экономическим / политическим изменениям окружающей среды, которые привлекают факторы роста рынка.
• В исследовании указаны самые быстрорастущие и самые медленно растущие сегменты рынка, что дает важную информацию о каждом ключевом элементе рынка. Игроки нового рынка начинают свою торговлю и ускоряют переход на рынок гибких сот. Прогнозируется, что деятельность по слияниям и поглощениям изменит рыночный ландшафт этой отрасли.

Этот отчет поставляется вместе с дополнительным набором таблиц данных Excel, в которых содержатся количественные данные из всех числовых прогнозов, представленных в отчете.

Что входит в предложение: В отчете содержится подробная информация об использовании и внедрении Flexible Honeycomb Industries в различных приложениях, типах и регионах/странах. Кроме того, ключевые заинтересованные стороны могут определить основные тенденции, инвестиции, движущие силы, инициативы вертикальных игроков, стремление правительства к принятию продукта в ближайшие годы, а также информацию о коммерческих продуктах, присутствующих на рынке.

Ссылка на полный отчет @ https://www.marketresearchupdate.com/industry-growth/flexible-сотовый отчет-2022-2027-361763

Наконец, исследование рынка гибких сотовых систем предоставляет важную информацию об основных проблемах, которые будут влиять на рост рынка. В отчете также содержится общая информация о бизнес-возможностях для ключевых заинтересованных сторон по расширению их бизнеса и получению доходов в конкретных вертикалях. Отчет поможет существующим или будущим компаниям на этом рынке изучить различные аспекты этой области, прежде чем инвестировать или расширять свой бизнес на рынке Гибкие сотовые телефоны.

Свяжитесь с нами:
[адрес электронной почты защищен]

Торт с пчелиной тематикой. Смотрите больше идей о пчелиных лепешках, b

Торт на пчелиную тематику. Посмотрите больше идей на темы «пчелиные кексы», «корм для пчел», кексы. 99 $ 8. Больше не ждите, просто закажите доставку тематического торта и ваш заказ будет доставлен любимому человеку вовремя. 1 — 18 января 2022 г. — просмотреть список изменений. Полная версия WordPress 5. CakeBee — служба доставки тортов № 1 в Интернете в Коимбатуре, Тричи, Ченнаи, Мадурае и Бангалоре. Фуражное кафе. 15 августа 2014 г. — Исследуйте доску Sweet Bee Cake Design «Тематические торты TMNT» на Pinterest.Вечеринка была посвящена пчелам, и я черпала вдохновение в дизайне супер-симпатичных приглашений. «Гудение» на улице в том, что эта вечеринка в моде! У него такая забавная и современная атмосфера со смелыми узорами и милой цветовой палитрой! Также обратите внимание на сказочный торт и кексы «Улей»; они просто прелесть! Эта вечеринка определенно вызовет трепет и… Украшения для торта в виде шмелей Виктория Тредер 16 мая 2014 г. 9:00. Вот несколько простых трехмерных топперов для кексов. Тема шмеля идеально подходит для этого! Пчелы в последнее время наделали много шума (извините, я не мог удержаться от этого!).Простые в использовании, подробные инструкции включены в упаковку. Есть несколько вариантов для рассмотрения: помадные пчелы, пчелиные торты. Эти топовые пирожные — колени пчелы, и они обязательно заставят вас гудеть от идей! Крошечная резиновая паста… нет 8 декабря 2021 г. — Исследуйте доску Марии Андухар «Пчелиные пирожные», на которую подписано 798 человек на Pinterest. Мы делаем только лучшие сладости в городе из мини-кексов, капкейков, тортов ко дню рождения и свадебных тортов. Мало того, это действительно красивая тема, особенно для весеннего, пасхального или летнего детского душа.эта ссылка открывается в новой вкладке. Изготовление пчелиных украшений. Мед, как одна из приправ, обязательно оставит ваших гостей в восторге. Детский душ (5) Цвет. Эту драгоценную вечеринку FIRST BEE-DAY PARTY представила Кэролин Вудс из A Touch of Style Events. Пригласите друзей вашего ребенка в свой улей, и наши идеи для вечеринки с пчелками займут их на несколько часов. Сливки из кокоса и лимонного сока составляют восхитительную комбинацию, а штрейзель придает приятный хруст. 99 — 58 долларов. Торты ко дню рождения на Хэллоуин (BS-9817) د.2. Найдите лучшие коллекции тематических вечеринок от HobbyLobby. Cake — американская рок-группа из Сакраменто, штат Калифорния, в состав которой входят певец Джон МакКри, трубач Винс ДиФьоре, гитарист Ксан МакКарди, басист Дэниел МакКаллум и барабанщик Тодд Роупер. С этой темой есть много разных вещей, которые вы могли бы назвать темой. текущая цена $6. Такие вещи, как «Первый пчелиный день малышки» или «Жуй на первый пчелиный день!» В любом случае, смэш-торт, который сочетается с этой темой, абсолютно восхитителен.Тематические торты добавят индивидуальности к особому случаю и ощутят сопричастность. 50 долларов. Если вы предпочитаете изучить наши готовые онлайн-продукты, нажмите здесь. Будь то тема лесной страны чудес, чтобы поприветствовать крошечного дровосека, вечеринка с усами, чтобы приветствовать будущего маленького джентльмена, который приходит в этот мир, милая черно-желтая вечеринка для будущего шмеля мамы, самолеты, поезда и автомобильный душ для маленького парень, который скоро будет в пути, или качающийся душ, чтобы поприветствовать маму и ее маленькую обезьянку… Индивидуальные пчелиные печенья на первый день рождения! Я действительно люблю все торты и печенье на пчелиную тематику в последнее время. Смажьте жиром и выровняйте форму для торта диаметром 15 см/6 дюймов и форму для торта диаметром 18 см/7 дюймов. 4 доллара. О, детка! Отпразднуйте новое прибытие с объявлениями о рождении, именными одеялами и многим другим! Креативность, которую вы вкладываете в приготовление торта из подгузников, также будет по достоинству оценена будущей мамой. Sweet as Can Bee Themed Kit Cupcake Cake 8 сентября 2019 г. — Исследуйте доску Мишель Одита «Пчелиный торт» на Pinterest. Когда вы планируете вечеринку, вы стараетесь сохранить… Дешевые товары для украшения торта, купить качественные товары для дома и сада напрямую из Китая. Поставщики: тематическая вечеринка с насекомыми. Мировой! Ограниченная по времени распродажа. Легкий возврат.Бесплатный пикап. Больше торта — это всегда хорошая идея. Наша пекарня расположена в очаровательном центре города Маунт-Холли. 25 — 3 доллара. 332 Silver Slipper Rd, Хукстаун, Пенсильвания, 15050, США. 99 (1) Начало страницы. Специальные торты на тему Хэллоуина Bee Sweet, капкейки на Хэллоуин, печенье на Хэллоуин, кексы на Хэллоуин и многое другое! Показаны все 9 результатов. Получите его, как только понедельник, 4 октября. 1/2. Но капелька бурбона в начинке не помешает. Есть только два варианта вкуса круглого торта, белый и шоколадный, но доступны все те же варианты глазури, что и в случае с тортом на день рождения и цветочным тортом.Она делала пчелиную тему для детской своей дочери. Есть несколько вариантов для рассмотрения: пчелы из помадки Шаг 3 – испечь пчелу. Sweet as Can Bee Theme Kit Двухъярусный торт $ 68. Sugar Bee Sweets — это пекарня-бутик, расположенная в центре Арлингтона, штат Техас. Выбор родителей. 56 $ 23. Дома или в любом месте у нас есть все, что вам нужно … Ознакомьтесь с нашим выбором топперов для торта с пчелиной тематикой, чтобы найти самые лучшие уникальные или сделанные на заказ предметы ручной работы из наших магазинов декора для вечеринок. Но теперь вы ищете «поговорки о торте для детского душа», которые дополнят ваш торт и сделают его по-настоящему идеальным.:) Этот топпер для торта «предназначен для пчел» от Thistle and Lace Shop — мой фаворит! Баннер с тортом на тему пчелы, баннер для стульчика, фон с тортом и первый день рождения пчелы CraftyCathy83 5 из 5 звезд (2144) 7 долларов. Он был наполнен подсолнухами и пчелами, чтобы украсить эту замечательную тему. Метод. Черные/деревянные канистры с пчелиным верхом — $5 7. Наполненный яркими желтыми цветами и ароматами восхитительного меда, это уникальный способ устроить девичник и, безусловно, незабываемый. Заметьте это.Лимонные капли для медовых капель и зеленая лакрица для цветочных стеблей Le Petit Prince Baby Shower Theme. Свадебный душ Кейк Попс. Настроить торт. 0 комментариев. От розовой глазури и клубничных веточек до подходящей начинки для торта — этот вариант хорош во всех отношениях. Вырежьте небольшой круг из бумаги для выпечки к 21 отзыву о пекарне Bee’s Knees «Моя мама заказала торт на мой день рождения здесь. Cute Cakes. com. Кафе Forage стремится стать желанным местом. .Мы предлагаем вкуснейшие торты, капкейки, пироги и другие вкусные сладости. Источник. Свадебные торты. Эшли Смит. Посмотрите больше идей на темы «пчела, кексы, пчелиная вечеринка». Один Торт Топпер Украшения С Сладкой Пчелой Для 1-го Дня Рождения Тема Выбирает Ребенка | eBay Даже если это серия вечеринок, вы… Мы используем только дизайны Эммы Бриджуотер на наших изделиях ручной работы. Вот несколько забавных поделок и принадлежностей на пчелиную тематику, которые украсят вашу удивительную вечеринку в пчелиной тематике: фигурки для кексов с пчелами от Penny’s Craft Studio.Источник Instagram: @best_cake_tula Торты для тортов: Если вы не хотите по-настоящему оживить готовый торт, неплохо было бы приобрести топперы для тортов Roblox. И это идеально подходит для летнего торта из подгузников с подсолнухами. «Ты мое солнышко, мое единственное солнышко» — идеальная тема для вашего детского душа, и у нас есть отличная идея! Торт из подгузников с подсолнухами идеально сочетается с нашей дверной вешалкой для больниц с подсолнухами, булавкой для мамы, гирляндой из подсолнухов и баннером для вечеринки. Посмотрите больше идей на темы «пчелиная вечеринка», «пчелиные кексы», «пчелиный детский душ».Голосование. Мы начали в 2014 году как команда мать / дочь. ПОДХОДЯЩИЙ РАЗМЕР — размеры топпера для торта составляют примерно 8 дюймов в высоту x 6 дюймов в ширину x 1/5 дюйма в толщину. Обратите внимание, что этот дизайн вафельной бумаги теперь предварительно вырезан для вашего удобства! Этот набор съедобной вафельной бумаги включает 16 различных изображений, каждое измерение 2. Обратите внимание, что кусок блеска находится на дешевом фоне, покупайте качественную бытовую электронику непосредственно из Китая Поставщики: Baby Girl Boy 1st Birthday Photo Background Bee Theme Cake Smash Portrait Background Подсолнухи Венок Забор Студийные фотографии Наслаждайтесь бесплатной доставкой по всему миру! .Она была одержима «Тортом для детского душа в стиле Бейонсе / Пчелиной королевы». Day Party Supplies Bee Day Party Supplies. Посмотрите больше идей о пчелах, кексах, пчелиных пирожных. Если не сезон, вы можете купить недорогую упаковку маленьких пластиковых цветов… YouTube работает Тестировать новые функции Пресса Авторское право Свяжитесь с нами Создатели 1.Удивительные торты. Какая милая тема для вечеринки на первый день рождения. С черным текстом, проштампованным вручную и запечатанным для создания поверхности, которую можно протирать (не подходит для мытья в посудомоечной машине). Набор из 6 украшений для кексов Queen Bee Cupcake Toppers. Человек производит зло, как пчела производит мед. Другие производители могут называть Layer Cakes 10-дюймовыми укладчиками, десятью десятками и 10-дюймовыми квадратами. Такой торт — прекрасный подход к теме. Betheme — лучший продукт, который мы когда-либо делали. Приглашение действительно задает тему с приглашением в форме подгузника в цветах темы.Сладкие торты. Многие предпочитают, чтобы пчелиная матка была целым тортом, но в этом дизайне вы ныряете в вкусный мед в сотах, а вокруг него летают съедобные пчелы. Горячая линия поддержки: +1 (570) 701-8028 Ознакомьтесь с нашим выбором игр на пчелиную тематику, чтобы найти самые лучшие уникальные или изготовленные на заказ изделия ручной работы из наших магазинов. Наши топперы для торта идеально подходят для украшения десертов «Babee» Тема торта «Шмель из подгузников», которую я сделала для клиента. Полностью собран на деревянной кирке. Украсьте крендельки желтой и коричневой (или черной) глазурью и добавьте конфетные глазки.Баннер «One» для стульчика для кормления — 10 долларов США. 14 тортов с подгузниками. Вам также может понадобиться клей для торта с этими украшениями. Магазин… Создание пчелиных украшений. Мне нравится пчелиная тематика этой свадьбы на ферме, она милая и уникальная, но не слишком банальная. через Баш. 9 февраля 2019 г. — Исследуйте доску zanem «Beecake pops» на Pinterest. Средства массовой информации. » Найдите много отличных новых и подержанных вариантов и получите лучшие предложения для торта «Шмель» с тортом «Счастливый день» для тематических украшений для вечеринки по случаю дня рождения по лучшим онлайн-ценам на eBay! Бесплатная доставка для многих продуктов! специальный торт из подгузников в виде пчелиного улья добавит 4 луны в атмосферу детского праздника и станет изюминкой!Привлекательность и уникальность — две основные особенности, которые будут в центре внимания всех зрителей!Эта идея свадебного торта для душа идеально подходит для деревенской вечеринки тема.Существует множество симпатичных канцелярских принадлежностей, которые можно использовать в качестве приглашений и благодарственных записок. 4. Размер: начинка: прозрачная: торт ко дню рождения в пчелиной тематике! количество. Bee Favor Box $ 0. 99. Этот торт потрясающий. 10 великолепных тортов для детского праздника Пчелиные тарелки, около 35-5 долларов 6. Такая расширенная панель параметров темы и инструмент Muffin Builder дают неограниченные возможности. Поделиться. В магазинах: ноль. Самовывоз и доставка доступны с Aisles Online. Далее вам понадобятся декоративные акценты для свадьбы в пчелином стиле.Выберите параметры. Скоро я поделюсь уроками по пчелиным пирогам, но я ОЧЕНЬ доволен тем, как они оба получились! Торт из подгузников в пчелиной тематике Для душа в стиле птиц и пчел этот торт из подгузников в виде улья идеально подходит! Источник: Фотография Элисон Сивек. Дешевые товары для украшения торта, купить качественные товары для дома и сада напрямую из Китая. Поставщики: тематическая вечеринка с насекомыми и пчелами. Ограниченная по времени распродажа. Легкий возврат.00.00 – ₨ 16 000. 8 из 18. От блинов в меду до пирога с медом. Милая фигурка для торта ко дню рождения с медовой пчелой — украшение для торта ко дню рождения с днем ​​пчелы Веселая маленькая игра слов представлена ​​в этой фигурке, вдохновленной пчелиными сотами. none О нас Пресса Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Связаться с нами Создатели Свадебные украшения в пчелиной тематике. Honie Bee’s находится в Honie Bee’s. 7 часов, 7 тортов, 40 яиц спустя я это сделал и я действительно горжусь этой горой 💪 Она наполнена шоколадными золотыми деньгами, сладостями, драгоценными камнями, конечно Смауг и Аркенстон.Дата коллекции: 08 апреля 2020 г. — 31 мая 2020 г. Добавить в избранное Наряд Bee-Day Outfit — рубашка-боди на день рождения пчелы — 1st 2nd 3rd — изготовленный на заказ топ и бант для малышей с медоносными пчелами — мальчик или девочка LampliteDesigns 5 из 5 звезд (561 августа 12 ноября 2021 г. — Изучите доску Шэрон Пфайфер «Кексы со шмелями» на Pinterest. После выпечки оставьте в форме до полного остывания, затем обрежьте излишки и пекановый пирог с медовым хрустом. Показан на 9-дюймовом круглом пироге; работает так же хорошо Тема. Подробнее 30. 00 $34. Какие милые украшения для торта в виде шмелей? Сделанные из пасты для лепки и помадки, вы можете зашуршать этими украшениями для торта в кратчайшие сроки.Для детского душа в стиле шмелей с детской коляской и пчелами MMF. Сладкие торты на тему спорта и игр с отделкой под дерево. Посмотреть нашу галерею. Вот некоторые популярные немецкие торты…. Поэтому я старался изо всех сил, и вот результат. Бургеры и хот-доги навсегда останутся любимыми блюдами всей семьи. Также с аккуратным сотовым дизайном. Дешевые украшения для вечеринок, купить качественный дом и сад напрямую из Китая. Поставщики: 1 комплект. Симпатичная маленькая пчелка. Тематическая вечеринка. Баннер. Торт Топпер. Латексный воздушный шар. Конфетти. все пользовательские торты ко дню рождения открыты сейчас.Простые синие, белые и золотые детали с маленькими звездами, а также верхушка для торта в виде короны объединяют эту идею детского праздника в книжной тематике. Группа была известна саркастическими текстами и невозмутимым вокалом МакКри, а также их разнообразными музыкальными влияниями, включая музыку кантри, мариачи, рок, фанк, иранскую народную музыку и т. д. Деревянный декор в виде пчел (3) — $2 4. Торт из подгузников также станет прекрасным подарком! Как всегда, я залез в интернет, чтобы почерпнуть немного вдохновения. 1003. Á Описание Тематические торты «Томас и его друзья» (BS-7639) Bee Sweet UAE предлагает изысканные праздничные торты, торты для особых случаев, свадебные торты и торты ко дню рождения, используя ингредиенты высочайшего качества и опираясь на свое мастерство, опыт и страсть.Подача 10. Торт 3D Land Rover. Это заказной продукт. 00 — 7 долларов. Показаны все 3 результата. Обратите внимание на шмеля, маленького ребенка и улыбающиеся лица. Кондитерские медовые изделия Бумажная игрушка пчелка на день святого валентина, день рождения. Пчел я тоже сделала из помадки. Красные и черные соты; розовые, голубые, желтые и коричневые стежки; синий и зеленый курсив и печатный текст; все готово для добавления в ваши любимые проекты Райли Блейк! Перейдите к коллекциям Bee Basics и Bee Backings, чтобы увидеть все, что есть в Bee 5. С игривым надписем со словами «Happy Bee-day» и несколькими медоносными пчелами, оживляющими топпер, это идеальный топпер для торта ко дню рождения для любителей пчел, садоводов, эко-воинов и стиля/цвета: Артикул: 2017861. Губка был ванильный с посыпкой (funfetti), а внутри были слои клубничного масляного крема и лимонного творога. $0. Торт на тему медоносной пчелы Outs. Наши талантливые кондитеры могут использовать фотографии, приглашения на вечеринки или хобби в качестве вдохновения для создания идеального индивидуального торта для вашего праздника.Торт был украшен красивой сделанной вручную кристаллизованной пчелой, чтобы придать ему идеальный вид. Для сладкого свадебного душа идеально подойдет тема медоносной пчелы. Горячая линия поддержки: +1 (570) 701-8028 Мой сын мечтает о торте Эребор на свое 12-летие. @sweetcreationsnapa. Смешайте 1 стакан сливочного масла и 1/3 стакана плюс 2 столовые ложки меда в… Пекарня Queen Bee Bakery ежедневно предлагает более 15 вкусов кексов! Приходите и посмотрите, какие кексы представлены сегодня. Пчелы любят цветы, и вы можете поспорить, что на этих вкусных тортах тоже должны быть цветочные акценты.8 долларов. Написал 6 минут назад. Фильтровать результаты. Красивые торты. 99 Быстрый просмотр. Поделиться на фейсбуке Custom Cake Gallery. Рейтинг 5. Сладкий, как пчела, тематический набор для торта за 23 доллара. Животные и насекомые (36) Семья (47) Природа (15) Фразы и выражения (2) Религия (1) Особые случаи (8) Новые сумки на молнии Bumble Bee по цене $1. Торт с дикобразом. Кейк-попсы — это легкое угощение… Идеально подходит для торта, чтобы отпраздновать вечеринку. Отпразднуйте день рождения и годовщину вас и вашего специального человека. Найдите минутку, чтобы оценить пчел и все, что они делают для нас, с последней коллекцией Deb Strain.Просто создайте большую картонную «пчелу» для детей с завязанными глазами, чтобы прикрепить ее к большому бумажному «цветку» на стене вашего дома. Секрет этого пятизвездочного орехового пирога заключается в его хрустящей начинке из меда, сливочного масла, коричневого сахара и орехов пекан. Есть несколько вариантов для рассмотрения: пчелы из помадки Взгляните на эти очаровательные идеи торта на тему медоносных пчел. Yellow Rock Candy, украшенный помадными пчелами. Ответ — да! Вы должны знать, почему одни имена работают лучше, чем другие, прежде чем выбирать их.05 — 36 канадских долларов. Пчелы из папиросной бумаги. Потрясающие торты «Реал Мадрид» (BS-8466) د. ️ В эти выходные следите за моим меню ко Дню Святого Валентина! Предварительная распродажа откроется после того, как I Bee First Birthday Party Decorations Set For Baby Showers Тематические принадлежности для вечеринок в стиле шмеля с баннером Happy Bee Day Cake Topper, желтым баннером для детского стульчика, Bee S для девочек и мальчиков Состояние товара: информация о новом продукте Bee Birthday Party Decorat Bee & Daisy Sugar Украшения Съедобные украшения для тортов, 12 шт. Используйте эти 12 украшений в виде пчел и маргариток от Culpitt, чтобы идеально украсить торты в садовой/летней тематике! Этот набор для украшения из сахара содержит пчел и белые цветки ромашки, которые отлично подходят для украшения кексов, печенья, тортов и многого другого. Уильям Голдинг. Дайте постоять, пока шоколад не застынет. Если они в сезон, добавьте в торт свежие цветы ромашки. Фейсбук. Набор украшений для вечеринки в честь первого дня рождения пчелы для детского душа. Принадлежности для вечеринки в стиле шмеля с баннером «Счастливый день пчелы». Используйте эти 12 сахарных украшений в виде пчел и маргариток от Culpitt, чтобы идеально украсить свои садовые/летние торты! Этот набор для украшения из сахара содержит пчел и белые цветки ромашки, которые отлично подходят для украшения кексов, печенья, тортов и многого другого.Самая популярная сессия — это DELUXE & DELUXE PLUS Cake Smash, тема которой выбрана клиентом. Посмотрите больше идей на темы «пчелки», «пчелка», «кексы». Я больше не делаю слишком много тортов для особых случаев, поэтому всегда весело стряхнуть пыль со старой скалки из помадки и приступить к делу. 00 Добавить в корзину; Подписывайтесь на нас! О. Мы гордимся тем, что создаем и внедряем инновации в торты, поэтому наши волшебные торты и … Купите праздничные атрибуты в веселой теме шмеля в нашем магазине. 25. Эти милые крендельки в шоколаде, украшенные шмелями, идеально подходят для дней рождения в стиле пчел, детских праздников и тематических вечеринок с изображением Винни-Пуха. Они станут восхитительным лакомством в качестве десерта или вкусной вечеринки! Вы получите 1 дюжину (12) шоколадных крендельков с шмелями, готовых к съедению в кратчайшие сроки! Кафе «Фураж» — Кафе «Фураж».Синий (1) Зеленый (1) Розовый (1) Красный (1) Отдел. ШАГ 6. Торты ко дню рождения PlayStation 4 (BS-8462) ï. Прыгать, чтобы. Заказывайте свежеиспеченные вкусные торты на день рождения и особые случаи. Желтая цветовая гамма идеально подходит для гендерно-нейтрального детского душа. Скидка 15% с кодом SENDLOVE2022 Слоеные торты включают 42 слоя квадратов размером 10 дюймов. Детские торты включают 20 слоев квадратов размером 10 дюймов. При заказе 4 или менее слоеных тортов они будут сложены, чтобы поместиться в конверт с фиксированной ставкой USPS Вышивка крестиком Лори Холт.500 фунтов стерлингов. Если вам нравятся эти угощения, пожалуйста, оставьте комментарий ниже и поделитесь ими со своими друзьями и семьей. 22 октября 2019 г. — Что включено? Баннер с 1-м BEE-DAY Bee Topper с персонализацией имени Детали: Бамбуковые палочки для баннера имеют высоту 12 дюймов. Варианты магазина. Мы начали возиться с украшением торта (результат просмотра слишком большого количества шоу тортов), и оттуда это превратилось в феерию съедобных изображений. Работая со вторника по субботу, мы подаем постоянно меняющуюся выпечку и сладости — вкусы каждой недели публикуются в социальных сетях во вторник утром, когда мы открываемся.О нас Пресса Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Связаться с нами Создатели Таймлапс торта в пчелиной тематике, который я приготовила на день рождения моей мамы! Внутри шоколадно-ванильный бисквит, покрытый масляным кремом из швейцарской меренги. Разогрейте бисквит и накройте свежими взбитыми сливками или откройте для себя прелести наших кремовых пудингов. 18 Первоначальная цена 26 долларов. Добавить в избранное Пользовательское имя Торт Топпер, Топпер для торта ко дню рождения Шмеля, Топпер для торта Happy Bee-Day, Топпер для торта ко дню пчелы, Украшения для вечеринки по случаю дня рождения пчелы невероятная свекровь.Воспользуйтесь нашей службой доставки продуктов уже сегодня! Учитывая, что торт будет центром притяжения на вашей вечеринке, он должен быть особенным. Этот пирог получается плотным и вкусным прямо из духовки. Слоеный торт Bee Joyful Deb Strain. 99. 98. Но это приятный штрих и добавляет особой сладости. Желтый торт ко дню рождения Ombre с изготовленным на заказ топпером в стиле пчелы; Тематическая вечеринка в честь первого дня рождения пчелы. Мой сын был счастлив 🥰 Изготовление пчелиных украшений. Это больше, чем просто тема WordPress. Возможна доставка в тот же день, в полночь и скидка 10% на первый онлайн-заказ.Покупайте Amazon – создайте декор для детской пчелы Amazon Baby Registry (3) – $2 4. Торт, еда и сладости: тогда, конечно же, торт! Я связалась с местной пекарней, и они испекли красивый торт с масляным кремом. Сопутствующие товары. Восхитительный ассортимент изображений на тему медоносных пчел делает красивое печенье для подарка или просто для удовольствия. Посмотрите больше идей на тему торт tmnt, тематические торты, день рождения tmnt. Топперы для тортов; Мы получаем комиссию за продукты, приобретенные по некоторым ссылкам в этой статье. 3к. Булочки и рулеты.Торт «Медовые соты и пчелы». Немного меда будет пчелой! Этот кекс гудел от волнения! ОДИН прекрасный торт в честь ОДНОГО! Тема: «Мистер Онедерфул» Цвета: черный, золотой, белый. Торт: «Сладкие угощения» от Натали Торжественные сеансы проводятся за 4–6 недель до фактического дня рождения, чтобы… Пчелиная тема Cake Smash Toronto Подробнее » СКИДКА 30%. Исследуйте другие популярные заведения питания рядом с вами от более чем 7 миллионов предприятий с более чем 142 миллионами отзывов и мнений от Yelpers.22 октября 2018 г. — Исследуйте доску Пэта Корна «Bee Cakes», за которой следят 5 306 человек на Pinterest. Торт на тему пчелиного меда. Когда дело доходит до красивого торта для детского душа, пчелиная тема предлагает множество прекрасных идей для торта. 99 У Лори Холт теперь есть несколько пчел в шляпе! В коллекции Bee Basics есть радуга, полная идеально сочетающихся тканей. Анализ характера чайного торта. детский душ в лесной тематике. Торт на день рождения с жимолостью, украшенный белым и коричневым молочным шоколадом, изображением пчелы, цифрой 9 и тонкими свечками.Queen Bee is 50 Cake Topper для женщин 50th Happy Birthday Cheer to Moms 50th Anniversary Тематическая вечеринка Поставки Украшения Отпразднуйте День матери Золотой блеск. «Вечеринка с единорогом» делится креативными идеями по декорированию, играми, едой для вечеринок и другими советами по планированию вечеринок. Офисные принадлежности для домашнего офиса и школьных занятий! Настройте стандартные, большие или тонкие размеры, 11 типов бумаги и более полумиллиона дизайнов! Бесконечные возможности персонализации снаряжения, такого же уникального, как и вы. Топпер для торта «Один» — 45 долларов.400 фунтов стерлингов. «Маленький принц» — одна из тех детских книг, которые никогда не выйдут из моды, как и эта вечная тема детского праздника. Серьезно, это лучшее место, где можно собрать все свои идеи в одном месте. Прикрепите пчелу к цветку: вы можете изменить многие распространенные игры для вечеринок, чтобы использовать тему сада, которую вы ищете. Поставьте лайк на нашей странице в Facebook, чтобы узнать больше об обновлениях, и получите онлайн-торт… Торт из подгузников и комбинезоны с пчелами Я создала торт из подгузников и комбинезоны для детского душа друга. Найдите больше забавных деталей пчелиной тематики на сайте Halfpint Design.С 253 вариантами вы нашли идеальный пост для этого. 32 результата. Показано 65–80 из 192 результатов. Этот бумажный баннер предлагает деревянные дюбели в желтую и синюю полоску, соты из желтой и золотой фольги, шмелей и черную нить. Торт на День Рождения в пчелиной тематике! Поскольку каждый торт изготавливается на заказ и украшается индивидуально вручную (вот почему они так хороши!), некоторые цвета и дизайны могут немного отличаться от продукта, представленного на картинке. Слоеный торт Райли Блейк — «Под западным небом» Грейси Ларсон.9 совместимость Полная совместимость с Elementor и Elementor Pro Полная совместимость с WooCommerce 6. Больше творческих тортов. Независимо от того, празднуете ли вы день рождения, выпускной или новорожденного, наши торты помогут вам отпраздновать это событие. Детский душ в лесной тематике Круглые торты двухслойные, и вы можете персонализировать торты и выбрать для них цветовую тему. Торты для девочек. Это также сделало бы красивый свадебный торт для весны и осени. Заменив самоформатный сахар медом, мы создали серию медовых блюд, напитков и десертов, которые произвели фурор в Сингапуре.Кроме того, с помощью этих пошаговых инструкций вы обнаружите, что сделать торт из памперсов в стиле джунглей легко и весело. Здесь вы найдете то, что вам нужно, независимо от того, ищете ли вы формулировку торта для определенной темы детского праздника, для гендерно-нейтрального ребенка … Мы просто пирожные с мороженым. . Свадебный торт на тему шмеля. Уитни. Назад Далее Запустить слайд-шоу . — Джанет Гилл, Кантон, Огайо. В дизайне розы и пчелы с надписью «торт» (как на фото). Почувствуй запах дождя и почувствуй ветер. Заказать Beehive Shoppe Bee Kitchen decor предлагает коллекцию кухонного декора в виде пчелы и улья, а также элементы кухонного настенного декора в виде пчелы.Сразу же разложите 2 дольки миндаля, чтобы они выглядели как крылья. Посмотрите больше идей на темы «бикейк попс, торт, пчелиные кексы». Спрятать. 15 долларов. 99 (2) 15 долларов. В любом случае фирменные торты добавят особый вкус. Изготовлен из высококачественного блестящего картона плотностью 250 г/м². 102 Подгузники Pampers Swaddlers (размер 1 или 2) Cake — американская рок-группа из Сакраменто, штат Калифорния, в состав которой входят певец Джон МакКри, трубач Винс ДиФьоре, гитарист Ксан МакКарди, басист Дэниел МакКаллум и барабанщик Тодд Роупер. Что это будет за торт с пчелиным тортом для темы Bee Party С милой пчелиной темой наш топпер для торта был создан для прекрасной вечеринки с раскрытием пола.769 отметок «Нравится», 9 комментариев — Bee’s Cakes N More (@beescakes__) в Instagram: «Тематический торт Джоджо Сива для маленькой милашки 💕💕💕 #girlycakes #jojosiwacake #tripledelight #cakeforgirls…» Подставка для торта Bees — Bees — Bee — Bee navy. Торты на заказ сделают любое торжество незабываемым. 600 фунтов стерлингов. 12 Десертов Дубов. Жужжащие красивые торты с пчелами. 00 Bee Theme Mr and Mrs Cake Topper. Торт «Человек-паук» для PlayStation (BS-8975). Топперы для тортов RSVP Party Decor красиво смотрятся на тортах, а также могут использоваться для многих других целей.Несмотря на то, что я был так занят, как пчела, готовясь к этой вечеринке по случаю дня рождения в пчелиной тематике, я знал, что хочу испечь два пчелиных торта. Вы получите удовольствие от наших разнообразных аксессуаров. Топпер для торта «невеста и пчела» также является приятным дополнением к торту. Красивые торты. Это будет нашим маленьким секретом. Bee topper — 4. 1. И хотя мы специализируемся на свадебных тортах и ​​всевозможных сладостях, не думайте, что студия дизайна Bee Box (художник, ранее известный как Sweet!), расположенная в Напе, Калифорния, является продуктом хобби. что серьезно вышло из-под контроля.Торт на тему динозавров. Воздушные шары — $2 9. Топпер для торта ко дню рождения в виде пчелы, топпер для торта в 3D-шейкере, вечеринка в честь дня рождения в стиле медоносной пчелы, персонализированный топпер для торта, тематическая вечеринка в виде шмеля, 1 или любой возраст TheLotusEclectic 5 из 5 звезд (117) Звездный продавец $ 27. Электронная почта или Телефон: Пароль: Забыли аккаунт? Зарегистрироваться. Блюдо с сыром и мясом всегда является фаворитом вечеринки. Если вы действительно хотите, чтобы ваша «тема пчел» качалась, подумайте о том, чтобы сделать несколько пчел для украшения. Вот некоторые из моих любимых предметов, которые я люблю держать под рукой, чтобы сделать наши занятия немного более причудливыми, творческими и веселыми! Идеи декора: Бумажные овсянки разных форм Шарики из тюля Пуфы из папиросной бумаги Мерцающие огоньки Вы нашли необычный торт для детского праздника! Поздравляем.Лучший торт с пчелиной тематикой 2021 года — 10 лучших тортов с медоносной пчелой на тему любви ₨ 3200. Живите полной жизнью и боритесь за свои мечты. Торт главного мастера Halo (BS-8974) د. Топпер для торта «Счастливый пчелиный день», Топпер для торта «Пчелиный день», День рождения в пчелиной тематике, Топпер для торта «Пчела», Топпер для торта «Счастливый пчелиный день», Топпер для торта ко дню рождения ThistleAndLaceDesign 5 из 5 звезд (6 626) Цена продажи 23 доллара. 00 Добавить в корзину; Bee-Day Printables — Набор 1 $ 0. Действителен только для заказа на вынос! НО было НАСТОЛЬКО вкусно. Попробуйте подать наши пышные пирожные с ангельской едой со свежей клубникой.Эти предварительно нарезанные, подобранные наборы идеально сочетаются друг с другом, поэтому вам не составит труда найти темы или цвета самостоятельно. Baby Shower Родитель Покупки. Войлочные пчелы и палочки для медовых гребешков — $5 8. Если у вас свадьба, день рождения, юбилей или что-то еще, чтобы отпраздновать с тортом, одно можно сказать наверняка: нестандартная насадка для торта сделает его особенным без особых усилий! 8 сентября 2019 г. — Исследуйте доску Мишель Одиты «Пчелиный торт» на Pinterest. 3 стакана ломтиков яблок, 2 стакана цельной свежей или замороженной клюквы, 2 столовые ложки меда, 1/3 стакана сливочного масла или маргарина, 1 стакан овсяных хлопьев, 1/2 стакана цельнозерновой муки, 1/2 стакана коричневого сахара, 1/2 стакана нарезанного орехи, 1/2 ч. л.Дизайн был вдохновлен приглашением. 18 дюймов (10% скидка HAPPY BEE DAY Banner Happy Beeday Happy Birthday Bee Bee Birthday Bee Cake Topper Тема пчелы DieCutDecor 5 из 5 звезд (801) 9 долларов. Жизнь полна красоты. bee_themed_baby_shower_room_dessert_table_red_velvet_shooters_lemon_cake_pops_bee_cake Изображения из этой галереи Персонализируйте свой идеально украшенный торт, чтобы отпраздновать любое событие и событие в Cakes.Как только мы протестируем достаточное количество тортов, мы начнем составлять списки самых популярных тортов с пчелиной тематикой.Торты ко дню рождения Цветочные торты Круглые торты Съедобные изображения Торты в виде листов Съедобные изображения Круглые торты Кексы Печенье Пироги Чизкейки Подносы для вечеринок Свадьбы и мероприятия Пекарня Связки. Выберите любой вкус торта, который вам нравится — мы выбрали простой рецепт сэндвича Виктория с использованием смеси из 5 яиц — и выпекайте в большой сковороде с полусферой при 160 ° C / газ 3 в течение 45-60 минут, пока шпажка, вставленная в середину, не выйдет. вышел чистым. Pinterest-приколите-это. (Пролистайте, чтобы узнать подробности!). 98 — 56 долларов. Возможно, вы знакомы с пирогом «Черный лес» (Schwarzwälder Kirschtorte на немецком языке), мраморным пирогом (Marmorkuchen на немецком языке), немецким яблочным пирогом (Apfelkuchen) и пирогом с пчелиным укусом (Bienenstich).Товары в этой категории являются цифровыми. Посмотрите больше идей на темы «торт, пчелиный торт, торт с пчелой». Sweet as Can Bee Theme Kit Round Cake $14. Новые сумки на молнии Bumble Bee по цене 1 доллар. 6. Например, мы использовали гипсофилу для этого детского душа, стеклянные банки, чтобы придать штрих шебби-шика, и добавили медовые соты к нашим вазам в качестве последнего штриха. Детская вечеринка в стиле Винни-Пуха невозможна без прекрасной желтой цветовой гаммы с добавлением красных вкраплений для драматического эффекта; Включение различных аспектов в тематический детский душ, посвященный Пуху, например, добавление пчел «Hunny», добавило очарования мероприятию; Какой невероятный десертный стол, наполненный великолепными творениями, такими как кексы с Винни-Пухом, … Идеи подарков в пчелиной тематике.Подумайте о целевой аудитории. Онлайн: ноль. Скидка 30% на выбранные товары! Опция «На вынос» — скидка 30% только на коробки для бенто. О настоящей свадьбе Рега сегодня рассказывает мой друг, редактор свадебного блога журнала West Virginia Living Magazine. Торт на тему павлина (BS-2314) Bee Sweet UAE Dubai & RAK, Торты на заказ на день рождения, юбилей, свадебные торты и для любого особого случая! Торт для детского душа «Шмель». Добавлять. У нас еще нет рецептов всех этих тортов на сайте, но мы постараемся сделать это в ближайшее время! Это был мой прошлогодний торт ко дню рождения в стиле пчелы и щенка (на 14-й день рождения), извините за очень позднюю запись.Есть несколько вариантов для рассмотрения: помадные пчелы Мы потратили 76 часов на исследование и сравнение 29 популярных моделей, чтобы определить лучший торт с пчелиной тематикой 2021 года, который вы можете купить. Закажите и заберите из местной пекарни, супермаркета или магазина мороженого и наслаждайтесь. Они добавят изюминку готовому изделию, или вы можете использовать их в качестве дополнительного реквизита. 99 Быстрый просмотр Скретч-карты 5 звезд (1) по цене $1. Сбрызните драже растопленным шоколадом, чтобы они выглядели как полоски шмелей. Торты в Дубае? Рас-Аль-Хайма? и по ОАЭ? Приходите к нам в гости на BeeSweet Dubai Mirdif & RAK.Подарочный мини-торт из подгузников. 4 Дикий. Испеките белый или лимонный пирог, покройте белой мастикой и добавьте украшения в виде пчел и жужжащую окантовку. 75,5 дюймов в высоту с бамбуковой палочкой, прикрепленной к задней части. Показано 49–64 из 192 результатов. Наши деревянные украшения для тортов с пчелиной тематикой добавят винтажный штрих к вашему классическому торту с медоносными пчелами или вечеринке по случаю первого дня рождения. На двенадцать лет моложе Джени и гораздо более низкий социальный статус, чайный торт изначально кажется рискованным кандидатом на брак.Вам также может понадобиться клей для торта с этими украшениями Магазин … Набор украшений для вечеринки в честь первого дня рождения пчелы для детского душа Тематические товары для вечеринок в стиле шмеля с баннером Happy Bee Day Cake Topper , желтое знамя стульчика для кормления, пчела s для мальчиков девушок Состояние деталя: Информация о новом продукте Декорат вечеринки по случаю дня рождения пчелы Делать украшения пчелы.Торт на пиратскую тематику. Также отлично подходит для вечеринки Happy Bee-day или вечеринки Mommy to Bee и Sweet as can Bee #beebabyshower #genderrevealideas #beetheme #mommytobee. Представьте себе двух- или трехъярусный торт с прекрасной желто-черной глазурью, а также милыми украшениями в виде пчел и топперами. Цена новой игры «Приколоть глаз к монстру» — 1 доллар. Баннер «One» для стульчика для кормления — 10 долларов США. 14 Ознакомьтесь с нашей подборкой игр на пчелиную тематику, чтобы найти самые лучшие уникальные или изготовленные на заказ изделия ручной работы из наших магазинов. 00 — 29 долларов. 1 совместимость GDPR Ready.Быстрый просмотр. Слоеный торт представляет собой ткань, состоящую из 42 кусков 10-дюймовых квадратов, по крайней мере, по одному кусочку от каждого принта в линейке дизайнера. 99 Быстрый просмотр Цена игры «Измерение детского животика» $1. Оставить комментарий. Похоже, это подсолнечный пирог с леденцами в виде шмелей. Имея в виду нашу тему медоносных пчел, мы использовали цветовую палитру из черного, белого и желтого цветов. Итог: если вы ищете легкий праздничный десерт, чтобы сделать вашу вечеринку незабываемой, рассмотрите эти красивые кейк-попсы как простой способ сделать это.Поместите его поверх домашнего торта для сладкого завершения вашего праздника! Торт на 1-й день рождения шмеля — торт на день рождения в виде шмеля, покрытый помадкой, с черной лентой и розовыми и желтыми ромашками. Вам также может понадобиться клей для торта с этими украшениями Магазин …. Добавьте их в простые домашние или магазинные кексы, чтобы получить сладкое удовольствие! Пиньята «Пиньята пчелиного улья» от Events by Social Graces. Все темы приветствуются, и я отправляю все. При оформлении детского душа пчелы внимание к мелким деталям будет иметь большое значение.Мои любимые идеи и элементы пчелиной вечеринки из этого милого … 11 сентября 2016 г. — Вдохновение на выпечку и укладку пчелиной тематики. Посмотрите больше идей на тему «Пчелиный день рождения», «Пчелиный торт», «Пчелиный торт». Я закончила торт этими мини-маргаритками с глазурью и… #chocolatecake #chocolate #chocolatecake Ознакомьтесь с нашим выбором топперов для торта с пчелиной тематикой, чтобы найти самые лучшие уникальные или изготовленные на заказ изделия ручной работы из наших магазинов декора для вечеринок. Мы доставим ваш заказ до вашего порога. Идеи торта для детского душа «Шмель» — 2019 — Baby Shower Diy.Итак, если вы хотите придерживаться традиционного торта — мы полностью согласны. Посмотреть рецепт. Добавить в корзину. 5 x 3. Из трех ее мужей (Логан Килликс и Джоди Старкс — первые два) Чайный пирог — единственная настоящая любовь Джени на протяжении всего романа. 99 Быстрый просмотр Декор для стен «Когда Бог создал меня» по цене $9. 7 дюймов в ширину (18 см) без кирки. Он почти * слишком красив, чтобы его есть. Размер топпера для торта приблизительно равен.00 — 71 доллар. Соберите все, что вам нужно, чтобы сделать торт из подгузников в джунглях. Разошлите приглашения в форме медоносных пчел как можно скорее, чтобы вы могли начать планировать самые сладкие вечеринки для самых сладких невест. ] Сам торт был лимонным пирогом с лимонным масляным кремом. Сопутствующие товары (1188) Торт «Замок» на 1 день рождения принцессы Диснея (1218) Торт на 1 день рождения мальчика (1180) Дора-путешественница и… Пчелиные пирожные и пирожные небольшого размера — мы делаем на заказ все, что соответствует вашим потребностям и желанию сердца! Bite-Sized Bee Cakes & Pastries создает торты ручной работы и тематические торты, кексы, печенье, кондитерские изделия и другую выпечку для любого случая, включая свадьбы, дни рождения, кухонные чаепития, детские души, крестины, вечеринки и праздники.Бесплатная стандартная доставка при заказе на сумму 49 долларов. Honey Crunch Pecan Pie с начинкой из медового масла. Еще одна популярная тема детских праздников и тортов — соты и пчелы. Одной из первых вещей, которую мы разработали, был стол, на котором были изображены черно-белая клетчатая скатерть, эти бумажные тарелки с белыми ромашками, черно-белые полосатые чашки и ярко-желтые салфетки. 00 Красивый торт с помадными боками и украшением в виде плюшевого мишки и летающих медоносных пчел для ваших близких. 98 — 37 долларов.Вам также может понадобиться клей для торта с этими украшениями. Магазин … 332 Silver Slipper Rd, Hookstown, PA 15050, United States. Выберите варианты Торты на тему спорта и игр Bee Sweet. 550 إ. Новые топперы для кексов Flame по цене $0. Мы предлагаем бесплатную доставку до двери в тот же день. С другой стороны, «Eva Fresh Bakery» больше рассказывает о ее работе. Торты на Хэллоуин (BS-9816) ï. Торт на тему мяча для регби. 55. У нас есть широкий выбор тематических тортов с восхитительными вкусами. Персонализированные продукты требуют обработки в течение 3 рабочих дней перед отправкой.Сделайте свой собственный восхитительный торт со взбитыми сливками и хрустящим миндалем и медовой начинкой. Закажите торт «Медовая пчела» на нашем сайте GiftzBag. Еда для ангелов, пироги с фунтами и пудингами. Просто покройте квадратный шоколадный торт зеленой глазурью, а затем поместите в центр несколько обычных красных бытовых свечей, связанных вместе этикеткой TNT, и все готово! 11 сентября 2016 – Вдохновение на выпечку и укладку пчелиной тематики. Я люблю цвета. Мне нравились более классические вечеринки на пчелиную тематику, и я решил пойти по этому пути.У нас есть кухонные фартуки на пчелиную тематику, сделанные в США, кухонные полотенца с пчелами, прихватки для духовки, рецепты и средства для приготовления меда, а также формочки для печенья с пчелиными сотами и штамп для печенья. Компания Cake Girl LLC специализируется на вкусных тортах и ​​десертах на заказ для ваших дней рождения. , детские души, свадьбы и другие специальные мероприятия. Если записки не осталось, к вашему подарку будет прикреплена обычная открытка. Закрывать. о нас. Или позвоните нам по телефону +971 50 985 4911 Создание пчелиных украшений. 9 января 2020 г. — Исследуйте доску Smchambers «Пчелиный торт ко дню рождения» на Pinterest.Посмотрите, как прекрасен торт «Пчелиный улей»! У вас есть идеальная тема — теперь, чем вы ее украсите? Я предоставляю все декорации для моих тортов в студии. В дополнение к небольшому свадебному торту предложите гостям десерт, чтобы насладиться им на ходу. Палочки увенчаны черными пластиковыми бусинами и черными и желтыми лентами. FlowerAura также предлагает доставку тематических тортов в полночь и в тот же день, чтобы обеспечить запуск меню персонажей и тематических тортов. (# 42R3X4) Наш набор вафельной бумаги Honey Bee… Нет предела совершенству, когда дело доходит до создания рождественских кейк-попсов.фейсбук; твиттер; линкдин; пинтерест; 3 уровня, подгузник, торт, -, сладкий, как, может, пчела, шмель, тема, Ca 3-х уровневый торт из подгузников — сладкий, как может пчела, шмель, пчела и ромашка, сахарные украшения, съедобные украшения для торта, 12 упаковок. Используйте эти 12 пчел и маргаритки. украшения от Culpitt, чтобы идеально украсить ваши садовые/летние тематические торты! Этот набор для украшения из сахара содержит пчел и белые цветки ромашки, которые отлично подходят для украшения кексов, печенья, тортов и многого другого. MonMon & Craft 24 шт. Ботворезы для капкейков с пчелами для детей на день рождения/свадьбу/декор сладкого торта/Пчелиная тема, раскрывающая пол украшения для вечеринок для кексов/черные золотые блестящие сотовые топперы для кексов.Посмотрите больше идей о пчелиных тортах, кексах, украшении тортов. Мы думаем, что они будут идеально смотреться, летая вокруг Lean на пчелиную вечеринку с разбитым тортом, напоминающим улей и украшенным крошечными съедобными пчелами. Торт на тему пчелиного улья. Создайте шумиху на своей следующей вечеринке с выпечкой, украшенной баннером Sweet As Can Bee Cake. Ваши гости будут приходить как пчелы на мед, если вы украсите свое заведение потрясающими украшениями в пчелиной тематике, включая раскрашенные терракотовые горшки, баннеры для пчелиных вечеринок и другие принадлежности для пчелиных вечеринок.Справка по доступности. Всего 24 доллара. Разнообразие салфеток — $6 11. Вы должны войти, чтобы оставить отзыв. Торт на день рождения в пчелиной тематике. Конец меню. Группа была известна саркастическими текстами и невозмутимым вокалом МакКри, а также их разнообразными музыкальными влияниями, включая музыку кантри, мариачи, рок, фанк, иранскую народную музыку,… Ваш дом или офис с нами. Сам торт представляет собой мягкий рассыпчатый торт, и я покрыла его своей любимой глазурью из взбитых сливок желтого цвета.Один торт будет для всех на вечеринке, а другой будет шикарным тортом для Сиенны. Сшитые сердечки, ножницы, иголки, нитки, цветы, ромбы, круги, звезды, следы от стежков и много ткани в клетку; все готово для добавления в ваши любимые проекты Райли Блейк! Перейдите к коллекциям Bee Backgrounds и Bee Backings, чтобы увидеть все, что предлагает Bee Bee Party Supplies & Baby Shower Decorations Ничто так не заставит ваших маленьких пчел жужжать, как правильные украшения. 5, предназначенный для печенья, изготовленного с помощью нашего прямоугольного резака 3 x 4.Это было совершенство. Коробка с хлопьями Bee Favors. Разделы этой страницы. Мы с гордостью предлагаем наши сладости в Тампе, штат Флорида, и ее окрестностях! У Лори Холт теперь есть несколько пчел в шляпе! Коллекция Bee Backgrounds полна великолепных элементов белого фона. 99 (3) 8 долларов. Бело-желтые фонарики с лентой — 7 долларов 10. Я создал эскизы комбинезонов и напечатал их на утюге на копировальной бумаге. Собирательство — это процесс, в ходе которого пчелы ищут лучший нектар. Хорошо, давайте… Цитаты о пчелах — BrainyQuote.00 Добавить в корзину; Bee-Day Printables — Набор 2 $ 0. Вот это кайф! Если ваша маленькая пчела сладкая, как мед, и любит жужжать, подумайте о том, чтобы устроить вечеринку в стиле шмеля. Категория: Тематические торты. Напишите мне, чтобы заказать торт из памперсов на заказ. Вскоре. Только онлайн. Обслуживает 10 человек. Быстрый просмотр 3-уровневая квадратная подставка для кексов. Пусть думают, что это торт-мороженое. 26 сентября 2020 г. · Джексонвилл, Флорида · Эта маленькая пчелка была одной из моих новорожденных выпускников, и она снова вернулась, чтобы задокументировать свой первый день рождения.Есть несколько вариантов для рассмотрения: Помадные пчелы Помадный торт с пчелиной тематикой Сделано для одного из наших аспирантов, защищающих свою диссертацию. Мстители 22755 (от четверти листа до полного листа) 27 долларов. Торт получил свое название Bienenstich (пчелиный укус) из-за медовой глазури и тонких кусочков миндаля. Например, если приколоть хвост ослику, то получится приколоть пчелу к цветку. Этот торт ко дню рождения в Майнкрафте очень легко сделать самому. Приглашения от ChicDesigns на Etsy были моей первой покупкой. Для идей детского душа с пчелиной тематикой вы можете добавить мед в печенье, торт и еду.Изготовленная на заказ бумага с мелованным покрытием для пчелиных баннеров. Праздники и случаи (8) Персонализация (1) Выбрать по позиции (1) Цена. Этот очаровательный ДЕНЬ РОЖДЕНИЯ В ТЕМЕ ШМЕЛА был представлен Сарой Осмотерли из Sugar Coated Mama. 8 из 5 звезд 8. Во имя любви к пчелам — Панель медоносных пчел — Фактический размер 12 x 44 дюйма. Сэкономьте на первом заказе. Медово-сахарную глазурь добавлять не нужно. В зависимости от ваших предпочтений, подумайте о деревенском шикарном торте, простом голом торте или очаровательном милом торте с лесными животными.Вы можете заменить песочное печенье любым хрустящим сахарным, лимонным или кокосовым печеньем, главное, чтобы размер каждого печенья был около 2 дюймов. ПРОДУКТ. Не действует при заработке и погашении Долларов ($). Есть несколько вариантов для рассмотрения: пчелы из помадки Будьте первым, кто оставил отзыв на “(1463) 2-х уровневый 1-й торт ко дню рождения – тема пчелы” Отменить ответ. Очень мило и очаровательно. 6 долларов. Список бесконечен. Он изготавливается на заказ с будущей фамилией невесты. Вам также может понадобиться клей для торта с этими украшениями. Магазин… Набор украшений для вечеринки в честь первого дня рождения пчелы для детского душа. Принадлежности для вечеринки в стиле шмеля с баннером «Счастливый день пчелы». Украсьте нашу подборку игр на пчелиную тематику, чтобы найти самые лучшие уникальные или изготовленные на заказ изделия ручной работы из наших магазинов.[Ниже, личная информация удалена. Перейти к рецепту. Чайный торт. Торт на тему доктора Макстаффинса. Нам нравятся приглушенные тона в дизайне торта, которые делают его элегантным, а маленькие крошечные пчелы по-прежнему делают его легким и актуальным. 9. Торт с пчелиным ульем. 29 мая 2019. Также испекла 2 десятка капкейков в тон. 00 и выше) Желтый масляный крем с 3D шмелем сверху со стоячим №1 белым с желтыми точками. Вся вечеринка наверняка будет гудеть об этом. Знак шмеля даст вам последовательность.Мы будем постоянно обновлять эту страницу по мере выпуска новых обзоров. Товары для вечеринок с животными и выпечка для отличных тематических вечеринок! Делаете ли вы торт ко дню рождения или создаете особую тему для вечеринки, просто просмотрите широкий ассортимент товаров для тематических вечеринок, украшений для тортов и кексов, а также сумок для угощений и многого другого! Добавьте копию о насекомых, рептилиях, жуках, пчелах, медоносных пчелах, животных джунглей, а также NAIWOXI What It Will It Bee Gender Reveal Товары для вечеринок — Bumble Bee Gender Reveal Украшения для детей Baby Shower, He or She Bee Banner, Bee Theme Table Cloth, Mommy Пояс для пчелы, бумажные веера, фигурка для торта, воздушные шары, украшения для вечеринки в честь ребенка NAIWOXI Принадлежности для вечеринки с указанием пола ребенка Включает в себя: 1 шт. Крышка для пчелиного стола 1 шт. Что это будет? Топпер для пчелиного торта 1 шт.56 $ 26. НАША ИСТОРИЯ. Детские торты. Мы упаковали всю прелесть фройо от Menchie’s (и многое другое!) в торт, который удивит и порадует ваших гостей. «Бутик Ever After Fairytales создал и разработал великолепную детскую вечеринку в пчелиной тематике. Автор: AngelFood4. Кусочки папиросной бумаги — это всегда забавный предмет для детей, и они определенно помогают этому шмелю выглядеть мило и пухло. Смажьте жиром 15-сантиметровую/6-дюймовую стеклянную миску из жаропрочного стекла или аналогичную. Сортировать по: Сортировать. Новый топпер для торта «С Днем Рождения с огненным значком» по цене $1.Вот что Уитни поделилась о планировании и оформлении вечеринки: «Очень весело проводить время с BEE!… Я все время пыталась придумать другую тему для нашего почти годовалого сына, поскольку пчелиная тема, казалось, подходила для чего-то девчачьего. . Вы можете настроить свои параметры ниже и оставить нам сообщение, и мы сделаем это специально для вас в магазине. 27 ноября 2019 г. — Пчелиные торты, печенье, вечеринка, идеи еды и напитков. Торт ко дню рождения с травяными блоками TNT. Посмотреть все. Наши талантливые сотрудники готовы предложить вам 15 тортов Minecraft «Приготовьтесь быть потрясенными»! 1.Баннер «One» для стульчика для кормления – $10 14 Изготовление украшений в виде пчел. Этот список предназначен для одного (1) «Что это будет?» Топпер из плотного блестящего картона. 38 долларов. спасти. Эти украшения, вдохновленные медом, я думаю, можно сказать, оооочень красивые. Печенье из сушеных цветов и другие 2 других торта и закуски: Самодельный элегантный торт What Will It Bee. Подставка для белого торта — $4 13. Нажмите alt + /, чтобы открыть это меню. Идеальный подарок для любого Baby Shower. Разогрейте духовку до 180C/350F/Gas 4. Добавить в избранное Больше цветов Помадка для торта «Шмель» — Помадная пчела — Помадка для шмеля — Помадка для насекомых — Помадка для пчел — Улей для помадки none none Торт в пчелиной тематике с чертополохом и кружевными украшениями для торта.И мы не можем забыть идеи подарков! Если вы мама для BEE, вы можете использовать эти потрясающие подборки, вдохновленные пчелами, чтобы начать регистрацию своего ребенка на Amazon. Баннер «One» для стульчика для кормления — 10 долларов США. 14 сахарных украшений в виде пчел и ромашек. Съедобные украшения для торта, 12 шт. Используйте эти 12 сахарных украшений в виде пчел и ромашек от Culpitt, чтобы идеально украсить торты на садовую/летнюю тематику! Этот набор для украшения из сахара содержит пчел и белые цветки ромашки, которые отлично подходят для украшения кексов, печенья, тортов и многого другого. Торт в стиле Барби с русалочкой.BEE PARTY ADDISON — Украсьте первый день рождения вашего малыша этой милой и очаровательной фигуркой для торта в виде пчелы. Лорен создала все ободки в виде пчелиных усиков, которые будут представлены на каждом мероприятии. 26 июня 2021 г. — Исследуйте доску Марии Андухар «Пчелиные пирожные», за которой следят 793 человека на Pinterest. Приготовьтесь к идеальному свадебному торту с этой великолепной насадкой для торта. Особенно мне нравится милый торт-улей. Читайте дальше, чтобы узнать о наших творческих приглашениях, украшениях, еде, подарках и играх Bumble Bee. Например, «Eva Bakery» звучит как очевидный выбор, но мало что говорит об услугах, которые они предлагают.00 из 5 на основе 5 оценок покупателей (5 отзывов покупателей) 28 канадских долларов. Не уверен насчет стоимости, но торт был восхитительным. Просто добавьте взбитые сливки и масло. У этой вечеринки есть много идей, которые вы могли бы использовать не только для вечеринки по случаю дня рождения, но и для гендерно-нейтрального детского душа. Кроме того, если вы можете разместить его на улице, он действительно оживает! Знак, Раскрытие пола пчелы, Знак от мамы к пчеле, Детский душ в пчелиной тематике, Топпер для пчелиного торта, Мед. Детские торты для душа. Bee Grateful демонстрирует пчелиные и цветочные тематические принты в теплых золотых и мягких серых тонах, идеально подходящих для добавления сладкой капельки меда в любой проект.99 (1) 4 доллара. Mama To Bee Cake Supplies. Это мои любимые от Minted: используйте белый цвет в качестве основного цвета при оформлении детского душа. Я использовал свой пчелиный штамп, чтобы украсить доску для торта, и использовал ленту, чтобы продолжить пчелиную тему. Белая глазурь — это ванильный масляный крем, а розовый — клубничный. Желто-черный детский душ с пчелиной темой — отличная тема для детского душа, особенно если вы не знаете пол своего ребенка. Клубничный торт. Ортопедический тематический торт. 51 доллар. Независимо от того, как вы планируете их использовать, топперы для торта определенно добавят изюминку и без того эпическому торту.Декор деревянной пчелы (3) — 2 доллара 4. Мне всегда приятно видеть этих малышей снова и наблюдать, как они растут (слишком быстро!) NBP предлагает несколько видов сессий Cake Smash. Заказывайте торты на день рождения в Hy-Vee! Настройте свой торт с днем ​​​​рождения сегодня. Фото: 100-слойный торт. Шоколадный или золотой торт, клубника, малина и черника с муссом из белого шоколада (начиная с дополнительных 10 долларов США.